Példa regressziószámításra
A regresszióanalízis két változó közötti összefüggés leírását a korrelációs együtthatóhoz képest sokkal pontosabban határozza meg. Ennek szemléltetéséhez nyissuk meg az előző fejezetben megismert Oven.sav állományt, majd válasszuk az Analyze / Regression / Linear parancsot (59. ábra).
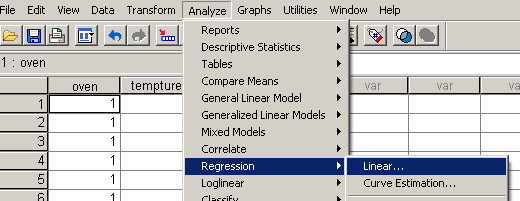
59. ábra
A megjelenő ablakban (60. ábra) a Dependent (függő változó) alá mozgassuk át a nyíl segítségével a Life of Components in minutes változót, míg az Independent(s) (független változó(k)) alá a Temperature in degree Fahrenheit változót, majd kattintsunk a Statistics gombra. A dependent a függő, míg az independent a független változót jelenti.
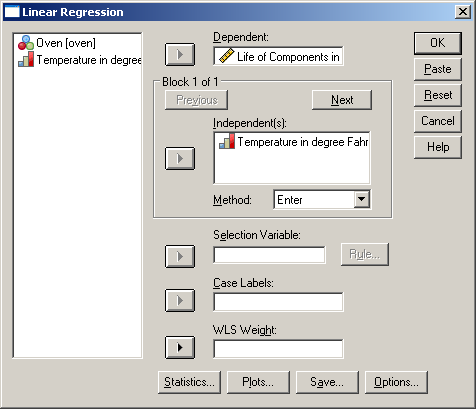
60. ábra
Az illeszkedésvizsgálathoz pipáljuk ki az Estimate és Model fit előtti négyzeteket, majd folytassuk a Continue, majd a Plots gombbal (61. ábra).
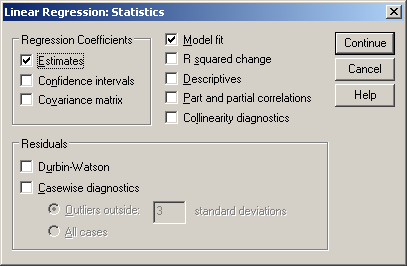
61. ábra
A homoszkedaszticitás (a hibatényező varianciája állandó) – mely a faktoranalízisnél is fontos – feltételének vizsgálatához a standardizált becsült értékre (ZPRED) és a standardizált reziduumokra (ZPRESID) lesz szükségünk. Ezért a Plots ablakban ezeket válasszuk ki (62. ábra).
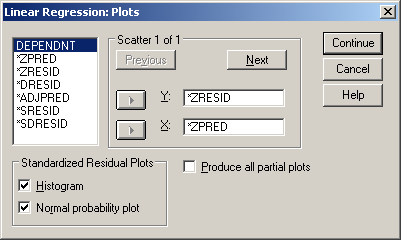
62. ábra
A táblázatban (20. táblázat) az r értéke a korrelációs együttható értékét (0,748) mutatja, míg az R Square a determinációs együttható értékét (0,560), ez a teljes szórás százalékos magyarázatát (56 %) jelenti. Az Std. Error of the Estimate a becslés standard hibáját jelenti (25,937). Minél kisebb ennek az értéke, annál eredményesebb a vizsgálat.
Model Summary(b)
|
Model |
R |
R Square |
Adjusted R Square |
Std. Error of the Estimate |
|
1 |
,748(a) |
,560 |
,532 |
25,931 |
| a Predictors: (Constant), Temperature in degree Fahrenheit |
| b Dependent Variable: Life of Components in minutes |
20. táblázat
Az ANOVA táblázat a regressziós egyenes által magyarázott (13667,556) és nem magyarázott (10758,444) szórásnégyzetet mutatja. Megtudhatjuk az F próba szignifikanciáját is, amelynek értéke kisebb, mint 0,05, tehát van kapcsolat (21. táblázat).
ANOVA(b)
|
Model |
|
Sum of Squares |
df |
Mean Square |
F |
Sig. |
|
1 |
Regression |
13667,556 |
1 |
13667,556 |
20,326 |
,000(a) |
|
|
Residual |
10758,444 |
16 |
672,403 |
|
|
|
|
Total |
24426,000 |
17 |
|
|
|
| a Predictors: (Constant), Temperature in degree Fahrenheit |
| b Dependent Variable: Life of Components in minutes |
21. táblázat
A t-próba szignifikancia szintje szintén kisebb, mint 0,05, így a hőmérsékletnek van befolyásoló ereje a sütő élettartamára. A Standardized Cofficients a regressziós egyenes meredekséget, míg az Unstandardized Cofficients adataiból a regressziós egyenes képletét lehet megtudni ( 22. táblázat).
Coefficients(a)
|
Model |
|
Unstandardized Coefficients |
Standardized Coefficients |
t |
Sig. |
|
|
|
|
B |
Std. Error |
Beta |
B |
Std. Error |
|
1 |
(Constant) |
263,000 |
19,328 |
|
13,607 |
,000 |
|
|
Temperature in degree Fahrenheit |
-55,111 |
12,224 |
-,748 |
-4,508 |
,000 |
| a Dependent Variable: Life of Components in minutes |
22. táblázat
A reziduálisokat az alábbi táblázat mutatja (23. táblázat).
Residuals Statistics(a)
|
|
Minimum |
Maximum |
Mean |
Std. Deviation |
N |
|
Predicted Value |
152,78 |
207,89 |
180,33 |
28,354 |
18 |
|
Residual |
-29,889 |
46,111 |
,000 |
25,157 |
18 |
|
Std. Predicted Value |
-,972 |
,972 |
,000 |
1,000 |
18 |
|
Std. Residual |
-1,153 |
1,778 |
,000 |
,970 |
18 |
| a Dependent Variable: Life of Components in minutes |
23. táblázat
A hisztogram segítségével azt a feltételt vizsgálhatjuk, hogy a rezidumok normálisan oszlanak-e el (63. ábra).
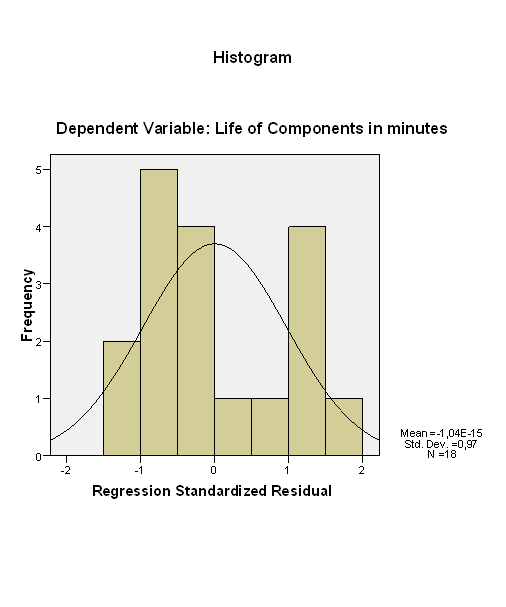
63. ábra
A 64. ábra a példa regressziós egyenesét mutatja meg, vagyis, hogy mennyire illeszkedik az egyenes a ponthalmazra.
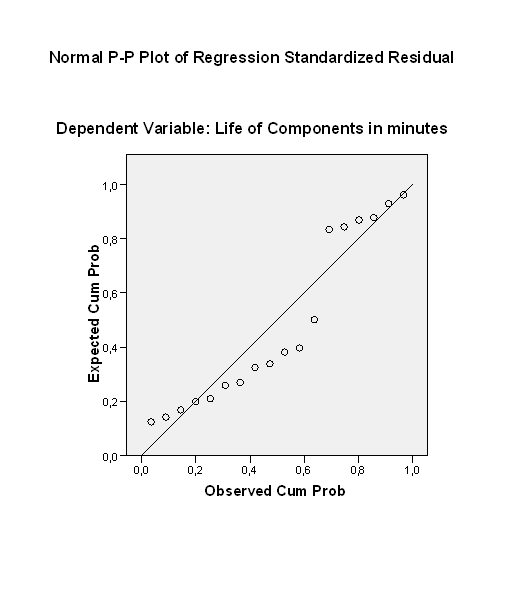
64. ábra