Példa klaszteranalízisre

Nyissuk meg a verd1985.sav állományt (72. ábra). A következő feladatban különböző életkori (age) kategóriákba tartozó és különböző családi állapotú (marital) egyedek adathalmazait szeretnénk csoportba rendezni matematikai (math) és nyelvi tesztjeiknek (language) megfelelően. Az adatbázisban egyéb változók is szerepelnek: pet (hány háziállatot tart), news (milyen újságot olvas), music (milyen zenét szeret), live (milyen típusú településen lakik), amelyeket most figyelmen kívül hagyhatunk (73. ábra).

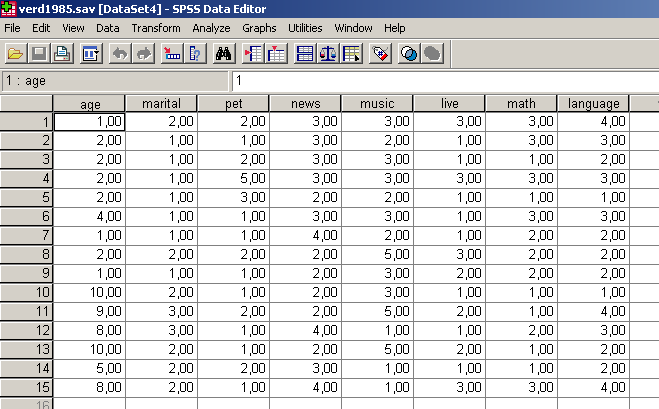
72. ábra

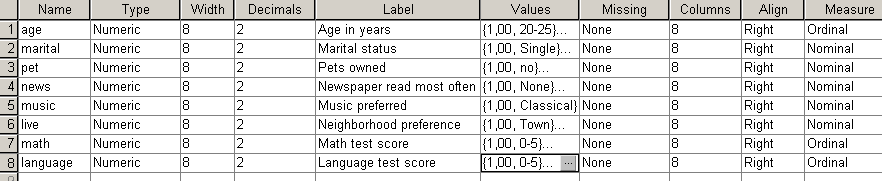
73. ábra

Mint láthatjuk, a math és language tesztpontszáma eltérő skálájú (a matematika hármas, míg a nyelv négyes skálás), ezért standardizálásra van szükségünk.

Válasszuk az Analyze/Classify/Hierarchical Cluster parancsot (74. ábra).

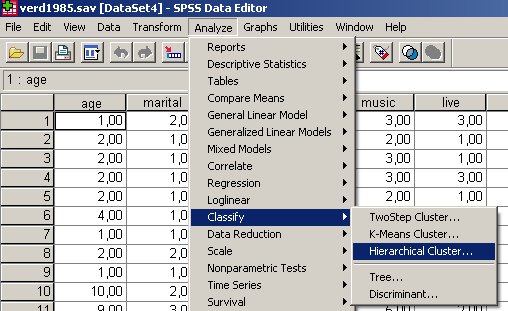
74. ábra

A Variable(s) alá mozgassuk át a vizsgálni kívánt Math test score és Languge test score változókat, majd kattintsunk a Method gombra (75. ábra).

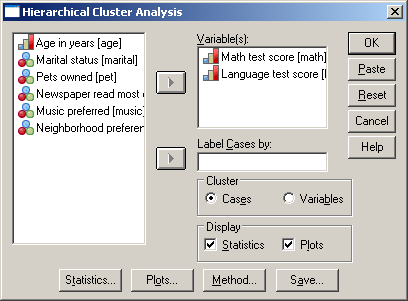
75. ábra

A megjelenő ablakban válasszuk a Ward’s methodot és Z score-nál a by variables mezőket (76. ábra).

76. ábra

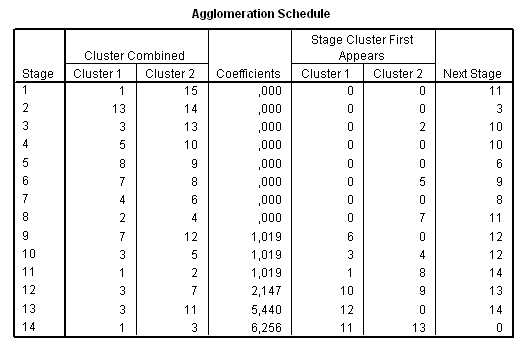
29. táblázat

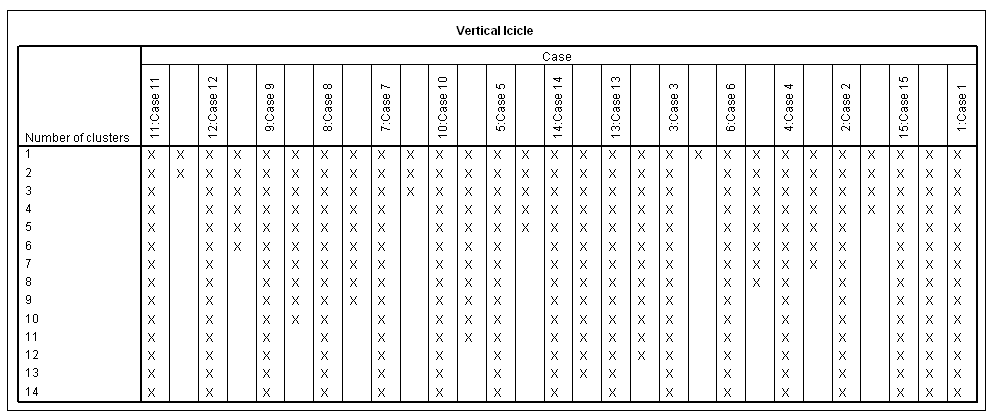
30. táblázat

A korrelációs vizsgálathoz válasszuk ki a már tanult Analyze/Correlate/Bivariate parancsot (77.ábra).

77. ábra

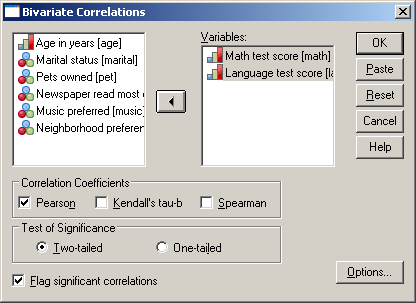
78. ábra

Correlations

*  Correlation is significant at the 0.05 level (2-tailed).

31. táblázat

A korrelációs analízisből látszik, hogy közepesen erős a korreláció a két változó között (31. táblázat). Így több érték fog egybeesni. Ennek ellenére most vizsgáljuk meg, hogy ha ez a feltétel nem teljesül, akkor mi történik.

Vizsgáljuk meg a továbbiakban pontfelhődiagram segítségével, hogy van-e kiugró érték az adatbázisban. Ehhez válasszuk a Graps/Legacy Dialogs/Scatter/Dot menüpontot (79. ábra).

79. ábra

Az előugró panelben válasszuk ki a Simple Clustert az esetleges kiugró értékek szemléltetéséhez, majd nyomjuk meg a Define gombot (80. ábra).

80. ábra

Ezután vigyük át a vizsgálandó változókat (Math test score and language test score) az Y Axis és X Axis alá. Amennyiben van egyedi azonosítóval rendelkező változónk, akkor a még jobb szemléltetés érdekében a Label Cases by (a pontok mellé írja az azonosítókat) vagy a Set Markers by (a pontokat színekkel látja el, majd az egyes színeket az azonosítóval párosítja) helyekre tehetjük (81. ábra).

81. ábra

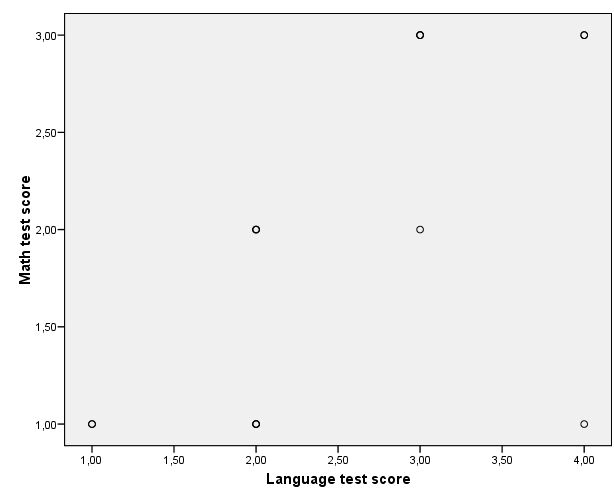
82. ábra

A pontfelhődiagram (82. ábra) azt mutatja, hogy van kiugró érték. Mivel viszonylag magas volt a korreláció és alacsonyak a skálák, így látható, hogy több érték is egybe esett.

Hogy szemléletesebbé tegyük a pontfelhődiagramot, hozzunk létre egyedi azonosítót (id) az egyes egyedeknek. Ennek érdekében váltsunk Variable View nézetre, majd írjuk be a név oszlopába az id változót, a tizedesvessző utáni értéket (decimals) csökkentsük 0-ra (83.ábra).

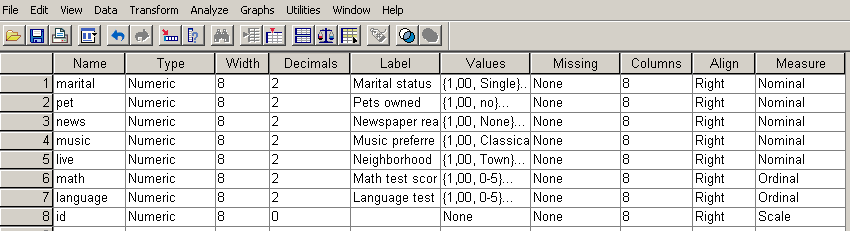
83. ábra

Ezután váltsunk vissza Data View nézetre, és gépeljük be az id változóhoz a sorok azonosítóit (84. ábra).

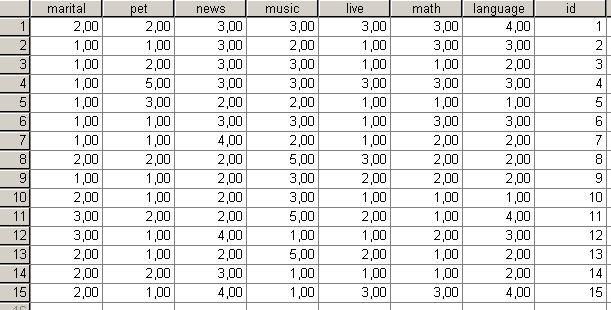
84. ábra

Ismét menjünk a Graphs/Legacy Dialogs/Scatter/Dot menüponthoz, majd válasszuk a Simple Scatter-t és kattintsunk a Define gombra.  A létrehozott azonosítónkat vigyük a Set Markers by mezőnévhez (85. ábra).

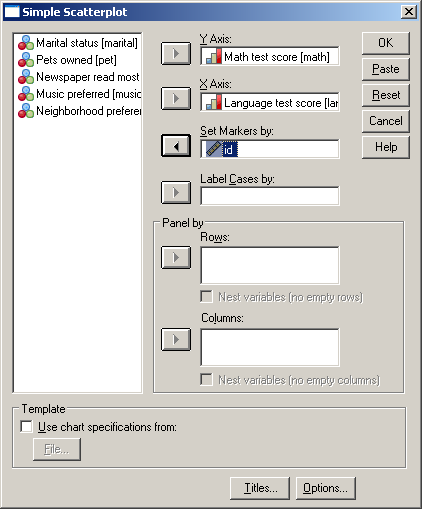
85. ábra

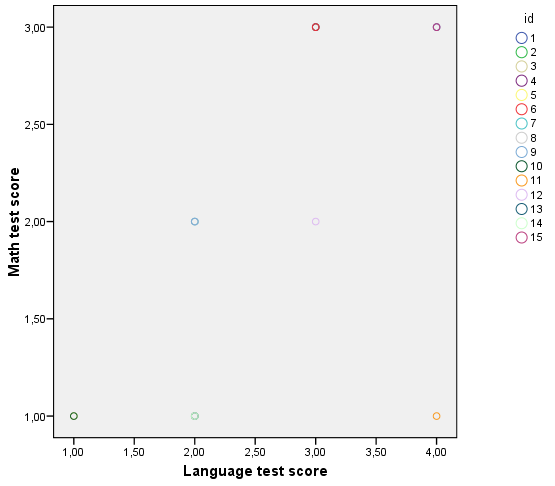
86. ábra

A szórásdiagramdiagram (86. ábra) jól szemlélteti, hogy nem mind a 15 elem esik más kategóriába, mivel egyes eredmények egybe esnek (ez a magasabb korreláció miatt lehetséges).

A kiugró érték megjelenítésének legalkalmasabb formája a dendrogram. Ehhez válasszuk az Analyze/Classify/Hierarchical Cluster paranancsnál (87. ábra) a Plots gombra (88. ábra) kattintva a dendrogramot  és kattintsunk a Continue gombra.

87. ábra

88. ábra

89. ábra

A Statistics gombra kattintva a proxy mátrixot és az Agglomeration schedule ábrát szeretnénk-e megjeleníteni (89. ábra), majd ismét a Continue gombra kattintsunk.

90. ábra

A Method gomra kattintva válasszuk Nearest neighbor (Legközelebbi szomszéd) módszert (90. ábra).

A klaszterek számának végső meghatározásában három szempontot vehetünk figyelembe. A  hierarchikus klaszterelemzés során kapott összevonási táblázat (Agglomeration Schedule) (32. táblázat) Coefficients (koefficiens) oszlopában található érték ugrásszerű növekedése, másrészt a dendrogram, harmadrészt a lehetséges klaszterek szakmai értelmezhetősége.

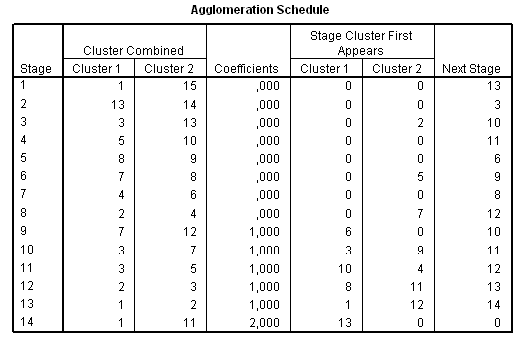
32. táblázat

A dendrogrammal együtt kirajzolódik (33. táblázat) a jégcsap diagram (Icicle) különböző tájolással (Vertical/Horizontal), attól függően, hogy mit választottuk a Plots menüpontnál.

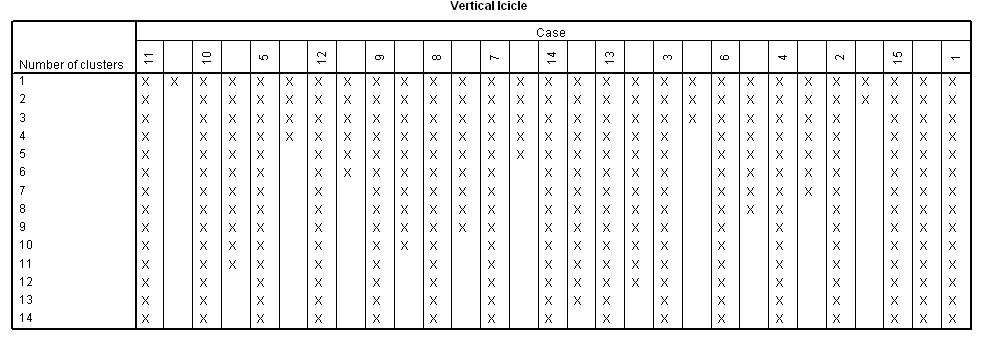
33. táblázat

A dendrogram segít eldönteni, hogy hány klasztert érdemes kialakítani. A dendrogramból (33. táblázat) jól látszik, hogy a 11-es a kiugró érték. El kell döntenünk, hogy ez a kiugró érték abnormális megfigyelés, vagy alulreprezentálja az alapsokaságban lévő csoport nagyságát.

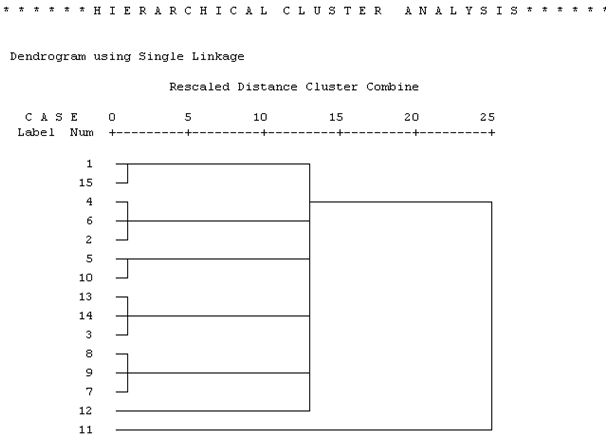
91. ábra

Mivel tudjuk, hogy melyik az az egyed (11-es számú), akit ki akarunk zárni, így nincs más dolgunk, mint kiszűrni. Ezért válasszuk a Data/Select Cases parancsát (92. ábra), majd If condition is satisfied alatt található If gombra kattintsunk (93. ábra).

92. ábra

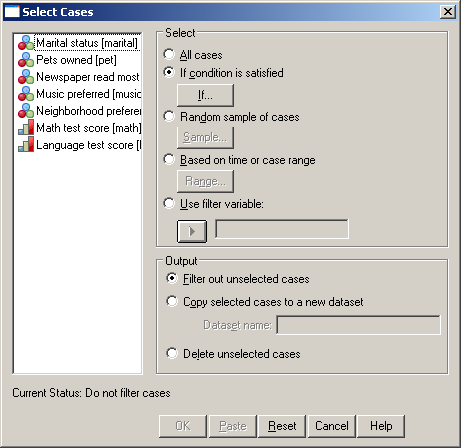
93. ábra

A szelektáláshoz egy tagadást kell alkalmaznunk, hiszen azt az egyedet nem szeretnénk, ha a vizsgálatainkban részt venne. Tehát a következő képletet alkalmazhatjuk: not (id=11). A jelen esetben a zárójel el is hagyható (94. ábra).

94. ábra

Az SPSS áthúzással jelzi, hogy melyik egyed nem fog szerepelni a vizsgálatban (95. ábra).

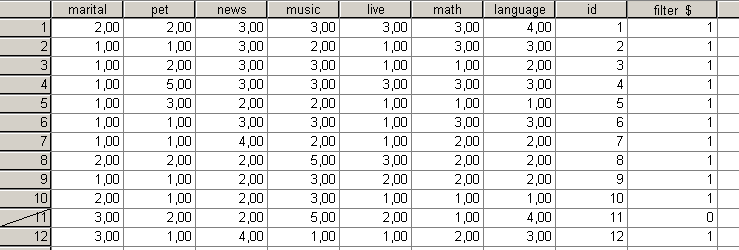
95. ábra

Ezt követően a Ward-eljárással haladunk tovább. Ez az eljárás akkor előnyös, ha a feltételeink teljesülnek, valamint a csoportok közel azonos szórásúak és minden csoport közel hasonló elemszámmal rendelkezik. Válasszuk az Analyze/Classify/Hierarchical Cluster parancsot (96. ábra).

Majd az előugró panelben válasszuk a Method gombot.

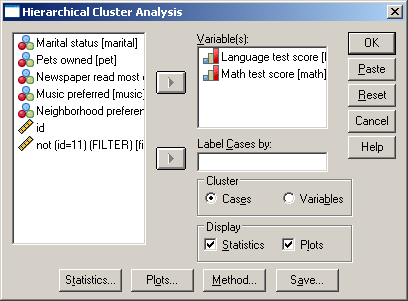
96. ábra

A Cluster Method lenyíló menüjéből válasszuk a Ward’s methodot és a Transform Values lenyíló menüjéből a None-t (97. ábra).

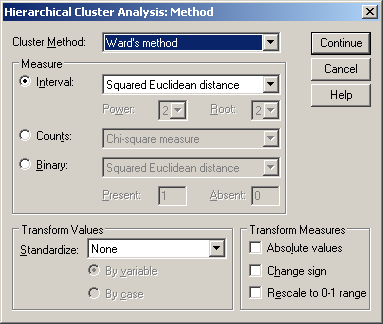
97. ábra

A 34. táblázat egyrészt megmutatja az egyes elemek, klaszterek összevonási sorrendjét (Cluster Combine oszlopok), másrészt segít meghatározni, a megfelelő klaszterszámot. A legnagyobb szakadék megkeresése úgy történik, hogy meghatározzuk az egymást követő koefficiensek különbségét, és a szakadék előtti klasztermegoldást tekintjük a jó klasztermegoldásnak.

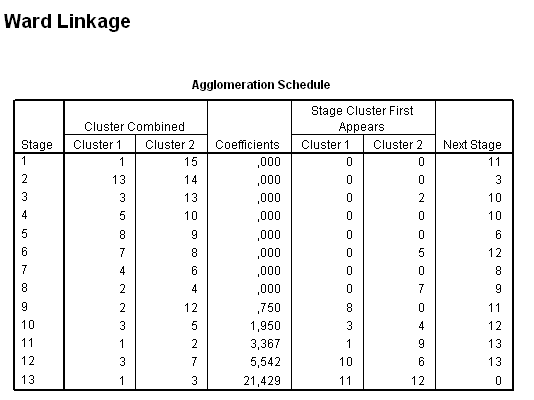
34. táblázat

Egy nagy ugrást (5,542-ről 21,429-re) láthatunk az utolsó két klaszter összevonása miatt. Ezt az ugrást megjeleníthetjük úgy, hogy a 4. táblázatra kétszer rákattintunk, majd kijelöljük egér segítségével az utolsó kofficienseket (coefficients) (35. táblázat) és a Formating Toolbarnál a Line diagramot választjuk ki (98. ábra).

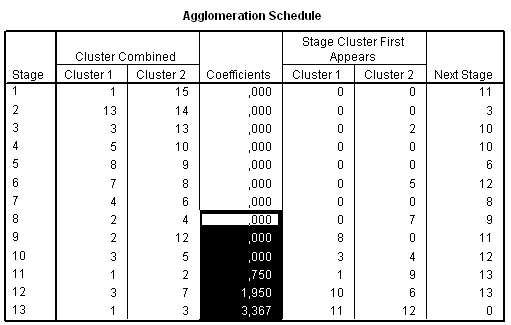
35. táblázat

98. ábra

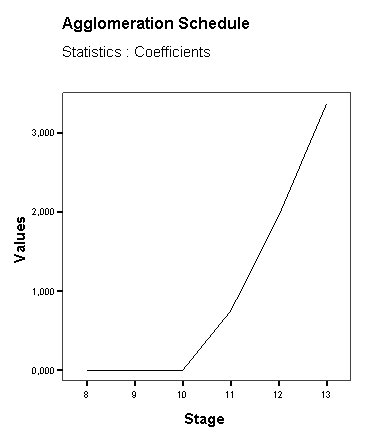
99. ábra

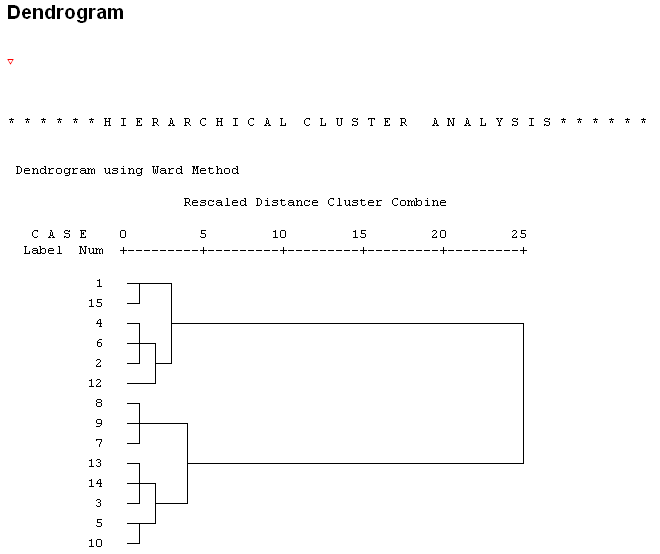
100. ábra

A dendrogram (100. ábra) azt mutatja meg, hogy hány összevonás után hány klaszter maradt. A dendrogram alapján két klasztert célszerű létrehozni. Mentsük el a kétklaszteres javaslatot. Ehhez vissza kell térnünk az Analyze/Classify/Hierarchical Cluster parancsohoz, és ott válasszuk a Save gombot. A megjelenő ablakban a Single Solution (egyetlen megoldás) Number of clusters értékéhez írjunk kettőt (101. ábra). Amennyiben több klasztert sejtünk, akkor a Range of solutions menüpontot válasszuk, ahol a Minimum number of clusters (minimális klaszterszám) értékhez írjuk az általunk vélt legkisebb klaszterszámot, míg a Maximum number of clusters (maximális klaszterszám) értékhez a legnagyobb klaszterszámot.

A legnagyobb távolság a horizontális tengelyt tekintve 3 és 25 között fedezhető fel.

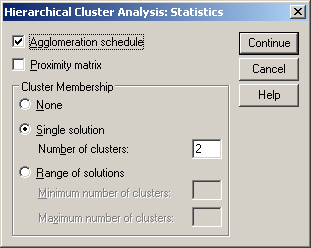
101. ábra

Az Output ablakban megjelenő alábbi ábra mutatja, hogy az egyes egyedek melyik klaszterbe esnek (36. táblázat).

Cluster Membership

36. táblázat

Az elemzést a klasztercentroidok (átlagok) alapján végezhetjük. Ehhez az átlag, elemszám és szórás értékeire lesz szükségünk. Az Analyze/Compare Means/Means parancsnál (102. ábra) a Dependent list-hez a Math and Language test score változókat, az Independent list-hez válasszuk a két Ward Methodot (103. ábra), majd az Options gombra kattintva keressük ki az átlag (mean), elemszám (number of cases), szórás (standard deviation) vizsgálatot (104. ábra).

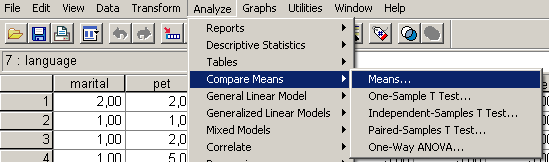
102. ábra

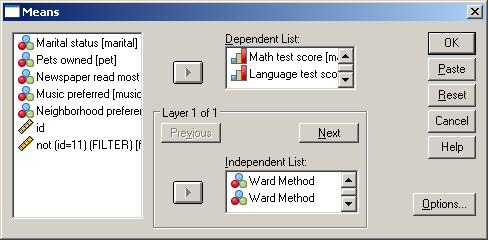
103. ábra

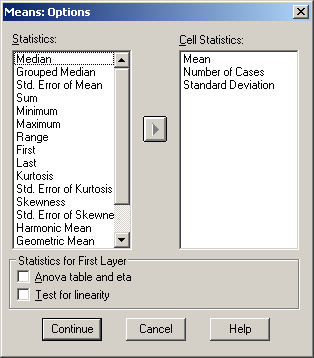
104. ábra

A három klaszteres megoldás nem hozott megfelelő eredményt, mert a 3 klaszternél a szórás nagyon csekély (37. táblázat)

Math test score Language test score  * Ward Method

37. táblázat

A két klaszteres megoldás jobb eredményeket hozott (38. táblázat).

Math test score Language test score  * Ward Method

38. táblázat

A szórásdiagram segítségével érzékeltethetjük a két klasztert. Ehhez a Graphs/Legacy Dialogs/Scatter/Dot menüpontjában mozgassuk át a 2 klaszteres (Clu2_1) Ward Methodot (105. ábra).

105. ábra

Az ábrán kék és zöld alakzattal jelöltük a kialakult két klasztert (106. ábra). A két klasztert elnevezhetjük (például 1. klaszter: ügyes nyelv és matek tesztet írók, 2. klaszter: gyengébb nyelv és matek tesztet írók.)

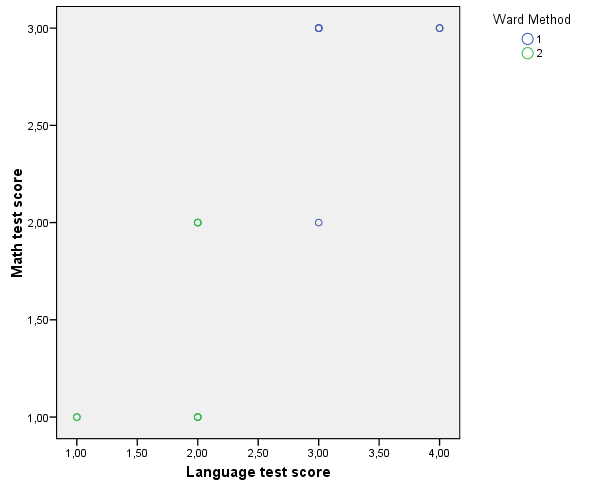
106. ábra