Példa a mutatószámok kiszámítására

A Floridai Egyetemen – 1989 ősze és 1991 tavasza között – a master képzésben részt vett hallgatók (forintra átszámított) kezdő fizetését szeretnénk megvizsgálni. A férfi és női hallgatók az egyetem 8 különböző főiskolai karán (1. agriculture – mezőgazdasági, 2. architecture – építés mérnöki, 3. building/construction – építészeti/épülettervezési, 4. business administration – üzleti tanulmányok, 5. forestry – erdészeti, 6. education – pedagógiai, 7. engineering – mérnöki, 8. fine arts – képzőművészeti) végezhettek.

Első vizsgálatunk során kíváncsiak vagyunk arra, hogy mekkora a kezdő fizetések

• számtani,
• mértani, valamint
• harmonikus átlaga.

Az elemzés elvégzéséhez először is nyissuk meg az SPSS példái között található University of Florida graduate saleries.sav nevű fájlt.

12. ábra

13. ábra

A File / Save As parancs segítségével mentsünk el a fájlt Floridai egyetemisták fizetése.sav néven.

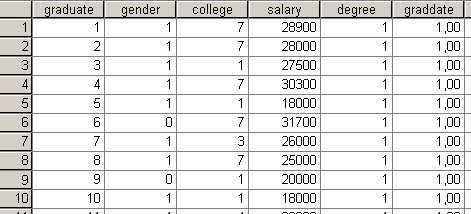
14. ábra Floridai egyetemisták fizetése.sav

Az átlagok számításához válasszuk az Analyze / Reports / Case Summaries parancsot. Vigyük át a nyíl segítségével a Starting Salary (kezdő fizetés) változót a Variables alá, majd kattintsunk az OK gombra.

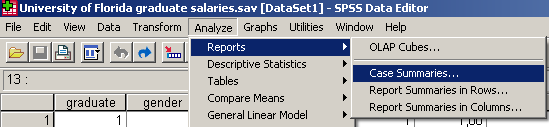
15. ábra

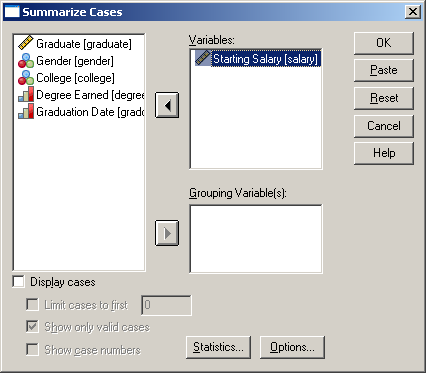
16. ábra

Ezután válasszuk ki a bal oldali listából az átlagot, geometriai átlagot és harmonikus átlagot és a Continue gombra kattintva megkapjuk az eredményeket.

17. ábra

Case Summaries

Starting Salary

3. táblázat

A táblázatból leolvasható, hogy a kezdő fizetések számtani átlaga 26062,20 Ft, a geometriai átlaga 25090,54, a harmonikus átlaga 24005,04 Ft. Jól látható, hogy a három átlag nem egyforma.

A vizsgálatunk során szeretnénk megtudni, hogy:

• Kinek a legnagyobb a kezdő fizetése?
• Kinek a legkisebb a kezdő fizetése?
• Mekkora az az összeg, amit legtöbben kapnak?
• Mekkora az az összeg, aminél ugyanannyian kapnak többet, mint ahányan kevesebbet?
• Mekkora a szórás, azaz mennyire tér el az egyes diplomások kezdő fizetése az átlagos kezdő fizetéstől?
• Mekkora az az összeg, amit összesen kapnak kezdő fizetésként?

A vizsgálat elvégzéséhez válasszuk ki az Analyze/Descriptive Statistics/Descriptives parancsot. Tehát a leíró statisztikák leíró menüpontját.

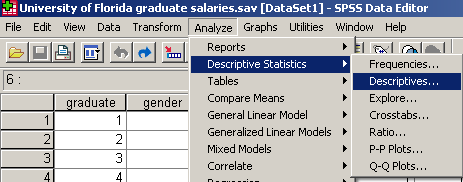
18 ábra

Az előugró Descriptives ablakban válasszuk ki, majd a nyíl segítségével vigyük át a Starting Salary (salary), azaz kezdő fizetés tételt a jobboldalra, a Variable(s) felirat alá. Majd kattintsunk az Options gombra. Ha véletlenül rossz tételt választottunk ki, akkor a nyíl segítségével vissza tudjuk vinni a baloldalra, majd a megfelelő elemet mozgassuk át.

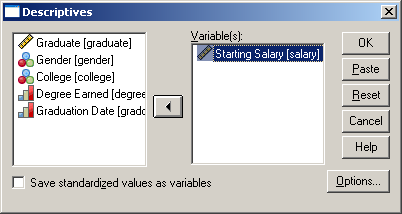
19. ábra

Ekkor egy újabb ablak ugrik elő, a Descriptives: Options. Pipáljuk ki az egér segítségével a kiszámolandó értékeket: az átlagot (mean), az összegzést (sum), a legkisebb elemet (minimum), a legnagyobb elemet (maximum) és a szórást (Std. deviation), majd kattintsunk a Continue gombra. Display Order alatt állíthatjuk be azt, hogy a változók milyen sorrendben szerepeljenek, amennyiben több változónk van. (Variable list: az adatbázis sorrendjében, Alphabetic: ábécésorrendben, Ascending means: az átlagok szerint növekvő sorrendben, Descending means: az átlagok szerint csökkenő sorrendben.) Végül kattintsunk a Continue gombra a folytatáshoz, majd az Ok gombra.

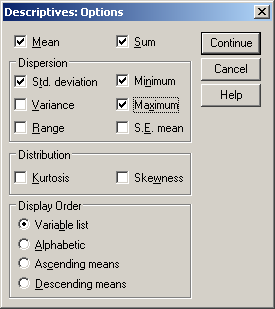
20. ábra

Az Output ablakban megjelenik egy táblázat (4. táblázat), ahol láthatjuk a vizsgálatunk kérdéseinek válaszait:

Az átlagos kezdő fizetés: 26064,20 Ft.

A szórás: 6967,982 Ft.

A legkisebb kezdő fizetés: 7200 Ft.

A legnagyobb fizetés: 65500 Ft.

Összes kezdő fizetés: 28670625 Ft.

Valid után látható érték az érvényes esetek számát jelzi, vagyis azt, hogy hányan adták meg a kezdő fizetésük összegét. 

Descriptive Statistics

4. táblázat

Amennyiben a táblázatokat szeretnénk átmásolni szövegszerkesztőbe, akkor kattintsunk a kívánt táblázatra, majd ez egér jobb gombjára, és válasszuk a Copy (másolás) parancsot, végül a szövegszerkesztőben a Szerkesztés/Beillesztés menüpontot. Így a táblázat könnyen formázható, az angol szavakat is átírhatjuk a magyar megfelelőikre.

Számoljuk ki a ferdeség és csúcsosság mutatóit, és ábrázoljuk hisztogram segítségével!

Az Analyze / Descriptive Statistics / Frequencies menüpontjában kattintsunk a Statistics gombra, és az előugró panelben a Discribution érték alatt található Skewness és Kurtosis értékeket pipáljuk ki, és nyomjuk meg a Continue gombot.

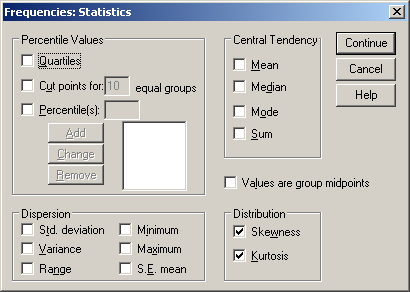
21. ábra

Ezután válasszuk a Chart gombot, majd jelöljük meg a Histograms és a With normal curve pontokat az alakzatok kirajzolásához.

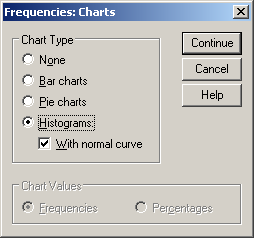
22. ábra

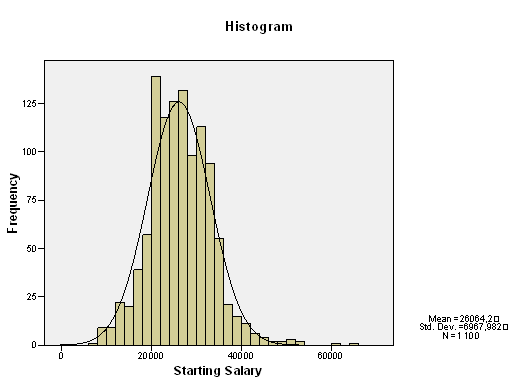
23. ábra

Az ábrából kitűnik, hogy a kezdő fizetés alakzata szimmetrikus. Ezt jelzi az alábbi táblázat is.

Statistics

Starting Salary

5. táblázat

A következő vizsgálat során az átlag, a módusz, a medián különbségére láthatunk példát, és ábrázoljuk őket.

A vizsgálatunk során az alábbi kérdésekre keressük a választ:

• Melyik főiskolai kart választották átlagosan?
• Melyik főiskolai karra jártak a legtöbben?
• Melyik az a főiskolai kar, amelyiket közepesen sokan választanak?

Emlékeztetőül, hogy milyen karok vannak a példában szereplő Floridai főiskolán:  agriculture – mezőgazdasági,  architecture – építőművészeti, building/construction – építészeti/épülettervezési, business administration – üzleti tanulmányok, forestry – erdészeti, education – pedagógiai, engineering – mérnöki, fine arts – képzőművészeti.

Az Analyze/Descriptive Statistics/Frequencies parancsot válasszuk a vizsgálat elvégzéséhez.

24. ábra

Vigyük át a Variable(s) alá a vizsgálni kívánt főiskolai kar (~College) változót, majd nyomjuk meg a Charts gombot.

25. ábra

A kördiagramos ábrázoláshoz válasszuk a Chart Type alatti Pie charts-ot (26. ábra).

26. ábra

College

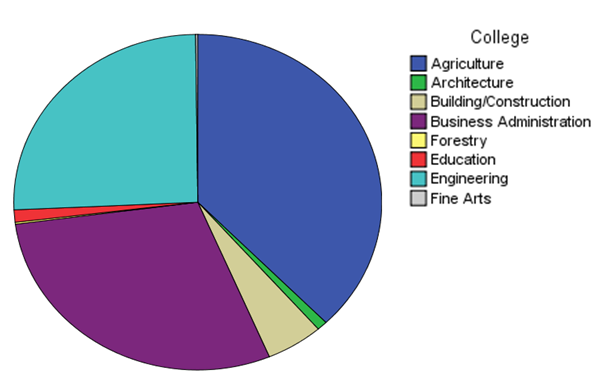
27. ábra

A Pie chart (tortadiagram) jól szemlélteti a 8 kar hallgatóinak a megoszlását (27.ábra).Mivel példánkban páros számú adat van, így a két középső értéket kell átlagolni. Ehhez a Pie Charts helyett a Histograms-ot kell választanunk (28. ábra). 

28. ábra

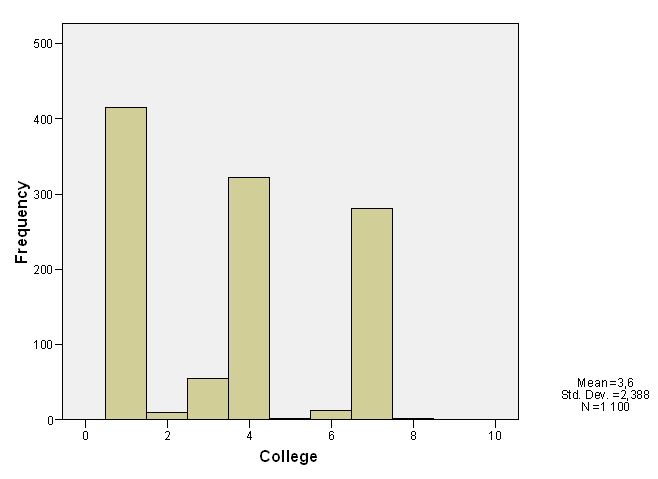
29. ábra

A hisztogram (29. ábra) segítségével ábrázolt adatokról a legegyszerűbb leolvasni a medián értékét, hiszen csak meg kell keresni az oszlopok közül a középsőt, és az lesz a medián.

A diagramokkal együtt a gyakoriságokat tartalmazó táblázat is megjelenik az Output ablakban.

College

6. táblázat

A fenti táblázat (6.táblázat) a főiskolai karok különböző gyakorisági megoszlásait mutatja. Az abszolút gyakoriság (frequency) azt jelenti, hogy az adott kar hányszor szerepel a rangsorban. A legtöbb hallgató (415 fő) a mezőgazdasági főiskolai karra járt, majd ezt követi az üzleti tanulmányok kar (322 fő) és a mérnöki kar (281 fő). A vizsgálatban részt vett többi kar hallgatói már jóval kevesebben vannak. A Percent az adatok százalékos megoszlást jelenti.

A relatív gyakoriság (Percent) az összelemszámhoz viszonyított gyakoriság (%-ban), azaz úgy kapjuk meg, hogy az abszolút gyakoriságot elosztjuk az elemszámmal és megszorozzuk százzal. Jelen esetben azt jelenti, hogy hány %-át teszik ki az egyes főiskolai karok hallgatói az összes kar hallgatóinak. Ez a szám például a mezőgazdasági főiskolai kar esetén 37,7 %.

A kumulatív relatív gyakoriság (Cumulative Percent) az adott sor és az azt megelőző sor – az első sor kivételével – relatív gyakoriságának összege százalékban kifejezve.

A Total, vagyis az összelemszám pedig a gyakoriságok összessége, azaz 1100 fő, ill. a relatív adatsoroknál nyilván 100% (kumulatív esetben nincs értelme).

Mivel a táblázatban a főiskolai karra vonatkozóan minden érték szerepel, így nem láthatunk különbséget az abszolút és a relatív gyakoriság között.

A két gyakoriság különbségének vizsgálatához töröljük ki a college oszlopból az első 15 értéket.

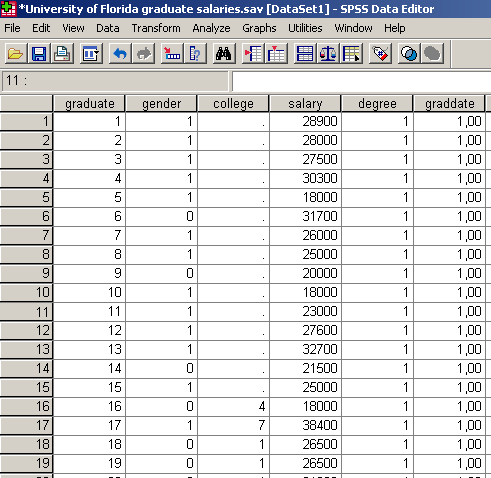
30. ábra

Ezután ismét végezzük el a gyakorisági vizsgálatot (Analyze / Descriptive Statistics / Frequencies). Míg a mezőgazdasági főiskolai kar esetében az abszolút gyakoriság (Percent) 37,2%, addig a relatív gyakoriság (Valid Percent) 37,7%. A Valid érték jelzi, hogy hányan válaszolták meg a melyik kar hallgatója kérdést. A Missing érték, pedig azt jelzi, hogy van-e hiányzó érték, azaz létezik-e olyan személy, aki nem válaszolt a kérdésre (30.ábra). (Az előzőleg kitörölt 15 érték itt jelenik meg.)

A következő táblázatból (7. táblázat) kitűnik, hogy a relatív gyakoriság figyelmen kívül hagyja a hiányzó adatokat. Hiányzó értékek esetén tehát a relatív gyakoriság helyett az abszolút gyakoriságot használjuk.

College

7. táblázat