Példa a korreláció kiszámítására
Nézzünk egy példát a korrelációszámításra. Vásárolni szeretnénk egy sütőt, de nem tudjuk, hogy a három fajta sütő közül melyiket válasszuk. Kíváncsiak vagyunk arra, hogy van-e összefüggés a sütők fajtája és az élettartama között, valamint a sütő élettartama és a sütéskor használt hőmérséklet között.
A vizsgálathoz nyissuk meg (File/Open/Data) az Oven tests.sav nevű fájlt (44. ábra).

44. ábra
Töröljük ki Variable View nézetben az utolsó, számunkra nem lényeges sort (45. ábra), majd váltsunk Data View nézetbe (46. ábra).

45. ábra

46. ábra
Végezzük el az összefüggésvizsgálatot a sütő fajtáit és az alkatrészek élettartamát figyelembe véve. Ehhez válasszuk az Analyze / Correlate / Bivariate parancsot (47. ábra).

47. ábra
A megjelenő Bivariate Correlation panelben (48. ábra) mozgassuk át a Variables alá az alkatrészek élettartamát (Life of components in minutes) és sütőket(Oven). A korrelációs kofficiensnél válasszuk a Pearson korrelációt, a kétoldali Two-tailed próbát, majd pipáljuk ki a Flag significant correlations-t, azaz jelezze csillaggal, ha szignifikáns a korreláció.

48. ábra
A megjelenő korrelációs táblázat (17. táblázat) viszonylag erős (-0,654) negatív korrelációt és szignifikanciát (csillagok jelzik) mutat a sütők és az alkatrészei élettartama között. A negatív előjel azt jelzi, hogy ez az összefüggés ellentétes. Minél kisebb a sütő fajtájának a száma, annál nagyobb a sütő alkatrészeinek élettartama. A Correlation is significant at 0.01 level azt jelenti, hogy a korreláció elfogadható legalább 1%-os szignifikanciaszint mellett.
Correlations
|
|
|
Life of Components in minutes |
Oven |
|
Life of Components in minutes |
Pearson Correlation |
1 |
-,654(**) |
|
|
Sig. (2-tailed) |
|
,006 |
|
|
N |
16 |
16 |
|
Oven |
Pearson Correlation |
-,654(**) |
1 |
|
|
Sig. (2-tailed) |
,006 |
|
|
|
N |
16 |
16 |
** Correlation is significant at the 0.01 level (2-tailed).
17. táblázat
Az adatokat jelenítsük meg pontfelhő diagram segítségével is, hogy szemléletesebbé tegyük a korrelációt. Válasszuk a Graphs/Legacy Dialogs/Scatter/Dot parancsát (49. ábra).

49. ábra
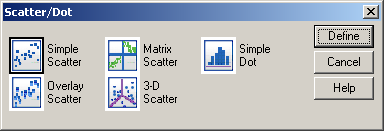
50. ábra
A Simple Scatter menüpontot válasszuk, majd nyomjuk meg a Define gombot (50. ábra).
A Simple Scatterplot ablakban (51. ábra) az X és Y (Axis) változók alá vigyük át a nyilak segítségével a sütőket (Oven) és az alkatrészek élettartamát (Life of Components in minutes), majd az OK gombra kattintva megjelenik ezek alapján a pontfelhő diagram.

51. ábra

52. ábra
A megjelenő ábra a szórásdiagram (52. ábra) szemlélteti a korreláció elvégzésekor kapott eredményt. A szórásdiagram két, vagy több változó együttes elemzéséhez, a közöttük lévő összefüggések feltáráshoz nyújthat segítséget. A pontfelhő alakjából és elhelyezkedéséből következtethetünk az adott változók közötti összefüggésre.
Most vizsgáljuk meg, hogy a sütő hőfoka és az alkatrészek élettartama között van-e összefüggés. Az előbbiek során bemutatott menetet kövessük: Analyze/Correlate/Bivariate. Ebben az esetben a Life of Components in minutes és a Temperature in degree Fahrenheit változókat válasszuk ki (53. ábra).

53. ábra
A korrelációs táblázat (18. táblázat) azt mutatja, hogy a két érték között szignifikáns kapcsolat van. Ez a kapcsolat is negatív korrelációt mutat, tehát minél magasabb a sütő hőmérséklete, annál kisebb az alkatrészek élettartama.
Correlations
|
|
|
Life of Components in minutes |
Temperature in degree Fahrenheit |
|
Life of Components in minutes |
Pearson Correlation |
1 |
-,782(**) |
|
Sig. (2-tailed) |
|
,000 |
|
|
N |
16 |
16 |
|
|
Temperature in degree Fahrenheit |
Pearson Correlation |
-,782(**) |
1 |
|
Sig. (2-tailed) |
,000 |
|
|
|
N |
16 |
16 |
** Correlation is significant at the 0.01 level (2-tailed).
18. táblázat
Nézzük meg ezeknek a változóknak is a szórásdiagramját az előzőhöz hasonlóan. Graphs / Legacy Dialogs / Scatter / Dot után válasszuk a Simple Scatter ikont (54. ábra).

54. ábra

55. ábra
A szórásdiagram mutatja, hogy alacsonyabb hőmérsékleten az alkatrészeinek az élettartama magasabb (55. ábra).
A következőekben parciális korreláció segítségével vizsgáljuk meg a három változó közötti összefüggést. Ehhez válasszuk az Analyze/Correlate/Partial parancsot (56. ábra).

56. ábra

57. ábra
Válasszuk ki a Life of Components in minutes és a Temperature in degree Fahrenheit változókat, majd kattintsunk az Options gombra (57. ábra).

58. ábra
Az Options ablakban jelöljük be következőket: Means and standard deviations és Zero-order correlations (58. ábra).
A parciális korreláció segítségével megvizsgálhatjuk, hogy valóban szignifikáns-e a változók közötti összefüggés. Ennek segítségével megtudhatjuk, hogy a két változó közötti kapcsolat valódi összefüggés-e vagy egy harmadik változó hatásának tulajdonítható, ami mindkettővel összefüggést mutat. A parciális korreláció táblázatát is az előzőleg már említett feltételeknek megfelelően elemezzük (19. táblázat).

19. táblázat