Alapfogalmak
A korreláció:
- A két változó közötti egyenes arányú, fordított arányú vagy hiányzó kapcsolat (pozitív, negatív vagy nem létező korreláció) lehet. Becslése az értékek ábrázolása alapján lehetséges.
- A korrelációs koefficiens legalacsonyabb értéke (abszolút értelemben): 0 (nincs lineáris korreláció), a legmagasabb +1,0 vagy -1,0 (tökéletes pozitív, ill. negatív lineáris korreláció)
- A korrelációs koefficiens értéke független a mértékegységektől.
- A kiugró értékek erősen befolyásolhatják a korrelációs együttható értékét. A kiugró érték lehet egy szabálytalan, torzult eloszlás eredménye, vagy lehet mérési hiba. A szóródási ábrán megjelenő, kiugró értékek esetén vizsgálatra van szükség. Célszerű ezeket kiküszöbölni. Ebben az esetben használható a Spearman féle rang-korreláció.
- Gyakran elkövetik azt a hibát, hogy a két változó közötti korrelációból ok-okozati összefüggésre következtetnek. Ha x és y között erős korreláció van, akkor ennek oka lehet:
- az y változásai okozzák az x változásait
- a x változásai okozzák az y változásait
- egy harmadik faktor mind az x-et, mind az y-t egy irányba (vagy – negatív korreláció esetén – ellenkező irányba) befolyásolja.
A kapcsolat szorosságát, a függőség fokát mérnünk kell (16. táblázat). Ennek mérésére a korrelációs együttható a szokásos mérőszám, amelynek sok tulajdonsága hasonló a szóráséhoz. A korrelációs együttható egy statisztikai mutató, azaz egy minta korreláltsága leírására szolgál, miközben a populáció változói közötti kapcsolat erősségét a korrelációs együttható mint paraméter határozza meg.

16. táblázat
Az összetartozó értékpárok halmazának mindegyik tagját egyenként átlagolhatjuk, és az egyes értékeknek a saját átlaguktól való eltérését vizsgálhatjuk. Az x, vagy az y szórásának számításakor ezen különbségek négyzeteit átlagoltuk (majd négyzetgyököt vontunk belőle), a korrelációs együttható számításakor az összetartozó különbségeket összeszorozzuk, és a szorzatok összegét (ezt más néven kovarianciának is nevezik) elosztjuk a négyzetes különbségek szorzatával. A korrelációs együttható két fontos tulajdonsága:
- A korrelációs együttható értéke független változók esetében 0.
- Lineáris függvénykapcsolatban lévő (nem sztochasztikus) változók esetében a korrelációs együttható abszolút értéke 1.
Minél szorosabb az összefüggés két változó között, annál jobban közelíti a korrelációs együttható abszolút értéke az 1-et; minél lazább összefüggés van két változó között, annál közelebb áll a korrelációs együttható értéke a 0-hoz (16. táblázat).
Fontos, hogy a korrelációs együttható az egyszerű, közel lineáris sztochasztikus kapcsolat esetében használható statisztika.
Ha két változó korrelációjának vizsgálata során az együttható értéke 0, akkor még nem biztos, hogy ezek függetlenek is! Ezért ilyenkor csak annyit mondhatunk: a két változó korrelálatlan.
A két valószínűségi változó korrelációját egy elméleti korrelációs együttható írja le. Ennek értékét a gyakorlatban becsléssel közelítjük meg. A becsléshez a szokásos módszer szerint a populációból mintát veszünk, majd a minta korrelációs együtthatóját kiszámoljuk, és meghatározzuk a becslés hibáját. A becslés hibájának ismeretében megmondhatjuk, hogy mekkora annak a valószínűsége, hogy a mintából számolt korrelációs együttható nem 0.
A korrelációs együttható előjele megmutatja, hogy az összefüggést jellemző egyenes emelkedő, vagy süllyedő. Görbére illeszkedő vagy annak mentén elhelyezkedő pontok ábrája jelzi, hogy a korreláció nem alkalmas az összefüggés jellemzésére, azaz nemlineáris a korreláció (43. ábra).
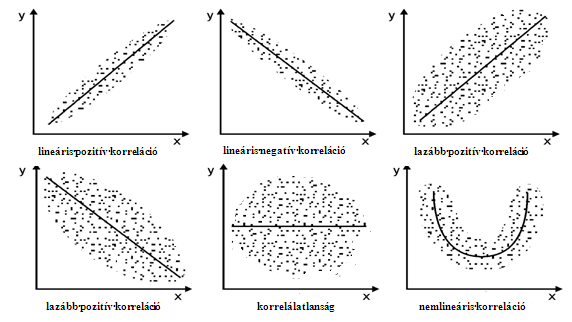
43. ábra
Gondolnunk kell arra is, hogy ha a korrelációs együttható szignifikáns, az még nem jelenti azt, hogy a változók között kapcsolat erős, vagy azt, hogy a kapcsolat jelentős lenne.
A korreláció mögött lehet ok-okozati viszony, de az is lehet, hogy a két korrelált változó nincs egymással ok-okozati kapcsolatban, hanem mind a kettő egy harmadik, közös októl függ. A korreláció magyarázata lehet a véletlen is, például, mind a két változó az idővel korrelált, és a közös tényezővel korrelált változók között gyakran van korreláció is. A tanulság, hogy az ok-okozati összefüggést logikai, vagy kísérleti úton kell bizonyítani.
Több változó esetében hasonló kapcsolat állapítható meg az ún. parciális korrelációs együttható segítségével. Ez azt mutatja meg, hogy mekkora lenne az x és y közötti lineáris korreláció, ha egy vagy több másik változót állandó szinten tartanánk.