I.6. Modellillesztés
A jelfeldolgozás során gyakori feladat az, hogy a mért jelekből kvantitatív következtetéseket vonjunk le a lezajlott folyamatokról. Ennek során az első lépés a jel (mérési eredmények) grafikus ábrázolása. Ez gyakran lehetővé teszi a mért adatok tulajdonságainak vizuálisan (szemmel) történő felismerését, s az első kvalitatív modell megadását. A mérési eredményeket leggyakrabban derékszögű koordinátarendszerben ábrázoljuk. A koordinátarendszerben a vízszintes tengelyen az időt (független változó), míg a függőleges tengelyen a mért mennységet (függő változó) ábrázoljuk. A grafikus ábrázolás során a kapott ábra akkor nem lesz torz, ha a két tengely beosztása megközelítően „egyforma”. Ezt követően olyan görbe vonalat kell húzni a mért adatokat ábrázoló pontok közé, hogy pontról pontra az adott pont és a görbe közötti távolság kicsi legyen (29. ábra). Hangsúlyozni kell, hogy nem a pontok közvetlen összekötése a cél, hanem a mért folyamat fizikai, kémiai, biológiai alapjait legjobban megközelítő kvantitatív összefüggés megtalálása – amelyet illesztési függvénynek is nevezünk.
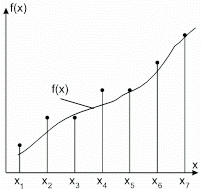
- ábra A mért pontokhoz illesztett görbe [7].
Az illesztési függvény kiválasztásakor figyelembe kell venni:
- az adott mérési pontokhoz tartozó elméleti megfontolásokat,
- az ábrázolás során kapott grafikont,
- a lehetséges illesztési függvények matematikai formuláját, együtthatóik jelentését.
Összefoglalva olyan illesztési függvényt kell választanunk, mely összhangban van a tapasztalatainkkal, a konkrét jelenség elméleti hátterével, és ugyanakkor a mért adatokhoz a lehető legközelebb van. Mivel a matematikában bizonyított tény, hogy bármely folytonos függvény tetszőleges pontossággal közelíthető polinomokkal, ezért mondhatnánk azt is, hogy válasszuk az illesztési függvényt elég magas fokszámú polinomnak. Ekkor azonban semmi sem garantálja, hogy a polinom együtthatói, valamint az illesztett függvény alakja tényleges fizikai jelentéssel bír.