I.5.1.1. Véges válaszidejű (Finite Impulse Response, FIR) szűrők
Ezen szűrők kimeneti jele csak a bemeneti jeltől függ. A FIR szűrőket konvolúciós szűrőknek is szokták nevezni, ugyanis működési elvük matematikai alapja két függvény (a bemenő jel és a szűrő függvény) konvolúciója. Definíció szerint, ha f és g a 
intervallumon értelmezett integrálható függvények, akkor ezen két függvény konvolúcióján az
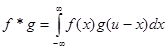
kifejezést értjük. Diszkrét esetben pedig legyen N számú mintánk egy jelből és tároljuk őket az x[N] vektorban, valamint legyen adott k darab, a szűrési karakterisztikát megadó valós számunk. Ezeket tároljuk az a[k] vektorban. Ekkor definíció szerint az a[k] és x[N] vektorok konvolúcióján az alábbi kifejezést értjük:
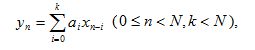
ahol yn az n-edik szűrt értéket jelöli. Az a[k] vektort a konvolúció magfüggvényének (kernel), a k számot pedig a konvolúció fokszámának nevezzük. A fenti formula egyben a digitális FIR-szűrők matematikai alakja is. A FIR-szűrőkre legegyszerűbb példa az átlagoló szűrő – más néven mozgóátlagoló szűrő. Ez a szűrő megfelelő tervezés és használat melltett a jelben levő véletlen zaj szűrésére kiválóan alkalmas. Maga a véletlen zaj olyan zaj, melynek spektruma adott frekvenciasávban nagyjából azonos teljesítmény sűrűségű. A véletlen zaj átlaga hosszútávon a nullához tart. Az átlagoló szűrő gyakorlatilag a jelben minden egyes pontot egy adott sugarú környezetének átlagával helyettesít. Matematikai alakban
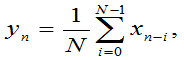
ahol N a környezet sugara. Látható, hogy az átlagoló szűrő képlete nem más, mint az xn jel és 1/N konstans konvolúciója Az átlagoló szűrő használatával azonban vigyázni kell, ugyanis az átlagolás ugyanis a jelben lévő zaj mellett a jel fel és lefutásának meredekségét is csökkenti. Ezért az átlagoló szűrő tervezésénél a fő szempont az, hogy mekkora legyen az átlagolás sugara, hogy az a jel alakját még ne torzítsa el, de a jelben levő zajt kiszűrje. Illusztrációként a 28. ábrán mutatjuk be az átlagoló szűrő hatásosságát. Az 0 felső részén egy szinusz függvény egy periódusa látható. Erre egy zavarjelet helyeztünk (középső görbe), majd ezt átlagoló szűrővel simítottuk (alsó görbe).
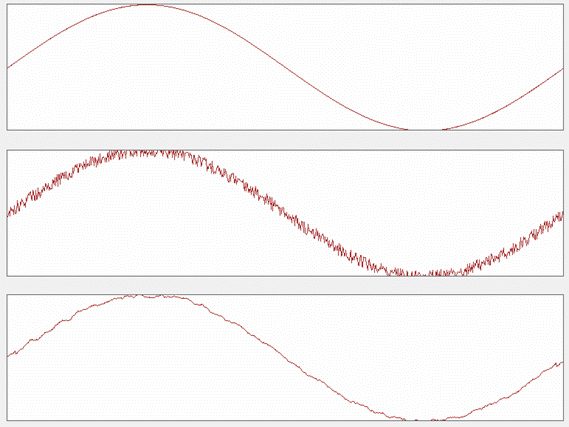
- ábra Szinusz függvény simítása átlagoló szűrővel.
- ábra Szinusz függvény simítása átlagoló szűrővel.
Mint az eddigiekből látható, a FIR-szűrőkkel a bemenő jel időtartománybeli viselkedését könnyen tudjuk befolyásolni. Azonban mit kell csinálnunk, ha a jel frekvenciatartománybeli viselkedését szeretnénk befolyásolni? Ebben az esetben a következő lépéseket kell végrehajtani:
- először a bemenő jelet Fourier transzformációval áttranszformáljuk a frekvencia térbe,
- az általunk megadott magfüggvénnyel beszorozzuk a jel spektrumát (elvégezzük a konvolúciót),
- a kapott spektrumot az inverz Fourier-transzformációval visszatranszformáljuk az időtérbe.
Bizonyítás nélkül itt jegyezzük meg, hogy a konvolúció műveletének a frekvenciatérben a szorzás felel meg.
A FIR szűrők nagy pontosságúak és jó elnyomási karakterisztikával rendelkeznek,