I.6.1. Legkisebb négyzetek módszere

Miután kiválasztottuk a megfelelőnek ítélt illesztési függvényt, meg kell határoznunk annak együtthatóit. A szakirodalomban a számítások elvégzésére a Gauss által javasolt legkisebb négyzetek módszerén alapuló algoritmust használják. Ez gyakorlatilag a következőt jelenti: az illesztési függvény együtthatóit úgy határozzuk meg, hogy a függvény egyenletéből szerkesztett görbe és a mérési adatok közötti („függőleges”) távolságok négyzeteinek összege minimális legyen (30. ábra).

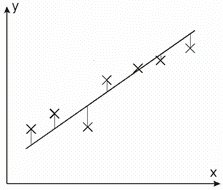
1. ábra: Legkisebb négyzetek módszere [7].

Matematikai alakban:

ahol y_j a mért érték, f(t_j) pedig az illesztési függvény értéke a t_j időpontban (a min szócska pedig egy bevett matematikai, optimalizáláselméleti jelölésmód, megegyezés szerint azt jelenti, hogy a feladatunk minimalizálási, azaz egyfajta – korlátozó feltételek melletti – szélsőérték meghatározása).

Az illesztés jóságát az r korrelációs együttható adja meg:

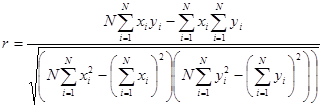
ahol . A korrelációs együttható értéke mindig -1 és 1 között van. A gyakorlati életben ezért ennek négyzetét az r²-et szokták használni az illesztés minősítésére. Minél közelebb van az r² az 1-hez annál jobb az illesztés. Élettani rendszereknél az 1-hez túl közeli r² értékek már gyanúsak, ugyanis ezeknél a rendszereknél összetettségük miatt a mérések során nagy a bizonytalansági tényező