I.4.2. Frekvenciaalapú jelfeldolgozás

Felvetődik a kérdés, hogy ha a valós világ analóg jelei az időben keletkeznek, és az időben változnak, akkor mi alapján mondjuk azt, hogy az adott jelben frekvenciák vannak, és a jelfeldolgozás szempontjából miért érdekes ez nekünk? Nos, a kérdés második felére a válasz, hogy az analóg jelek mindig zajjal terheltek, s a jelfeldolgozás egyik legfontosabb feladata a zajoktól történő megszabadulás, vagy annak hatásainak csökkentése. A kérdés első felére pedig a válasz a következő:

1822-ben Fourier francia matematikus, fizikus bebizonyította, hogy minden periodikus függvény egyértelműen felírható megfelelő amplitúdókkal és fázisállandókkal bíró harmonikus rezgések összegeként. Matematikai formában

ahol a rezgés körfrekvenciája. Emiatt tudjuk mondani azt, hogy a periodikus jeleket frekvencia alapon is feldolgozhatjuk. Az  és  együtthatókat az adott jel Fourier- együtthatóinak nevezzük, melyek az alábbi formulával számolhatok ki:

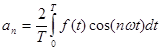
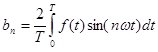
Az  a jel stacionárius egyenáramú komponense, melynek értéke a jel egy periódusra átlagolt középértéke. Matematikai formában:

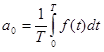
A jel Fourier sorában alapharmonikusoknak nevezzük a  és a  tagokat, a  és a  tagokat pedig felharmonikusoknak.

Feladat.

Határozzuk meg a Fourier sorát az f(t)=2t függvénynek a  intervallumon.

Megoldás.

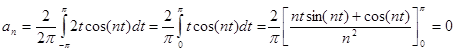
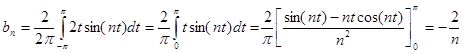
Ennek alapján:

Ezért az  függvény Fourier sora a  intervallumon:

A téma részletesebb tárgyalására nem térünk ki, de a Fourier-sorfejtés témakörében a mélyebben érdeklődők számára alábbi magyar nyelvű oldalon további gyakorló feladatok találhatóak. A Fourier együtthatók szimbolikus kiszámítására kiválóan alkalmas például a Wolfram Mathematica Online Integrator.

A Fourier-sor előbb megadott felírási módja a Fourier-sorokkal végzett műveletek során a terjengőssége miatt nem mindig célszerű. Megjegyezzük, hogy a komplex számok használatával a felírási mód jelentősen egyszerűsíthető. Bizonyítás nélkül közöljük a Fourier sor komplex számokkal felírt alakját:

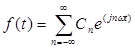
ahol j a képzetes egység, és

jelöli a komplex amplitúdót.

Ha egy  periodikus jel Fourier sorában a szinusz függvények amplitúdóit ábrázoljuk a szinuszok frekvenciáinak függvényében, akkor megkapjuk az illető periodikus jel színképét, más szóval spektrumát. Periodikus jelek spektruma vonalas, azaz csak diszkrét frekvenciaértékeken létezik nem zéró frekvencia komponens. A valós életben a jeleknek csak viszonylag kis része periodikus. A Fourier sorfejtés viszont csak periodikus jelekre teszi lehetővé az átalakítást az időtartományból a frekvenciatartományba és viszont. A kérdés az, hogy ki lehet e a módszert terjeszteni nem periodikus jelekre is. Mivel a nem periódusos jel felfogható úgy is, mint olyan periodikus jel melynek periódus ideje , ezért a válasz igen. Nem periodikus jeleknél a  határátmenet alkalmazása miatt a spektrum vonalak távolsága , ezért a spektrum folytonos. Bizonyítás nélkül kimondjuk, hogy ekkor a Fourier sorban az összegzés integrállá alakul, mert az integrál nem más, mint a végtelen kicsi  tartományokra vett függvényértékek összege.

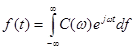
ahol  a komplex értékű folytonos amplitúdó függvény, melyet az  függvény Fourier-transzformáltjának nevezünk. Matematikai alakban:

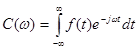
Komplex írásmód alkalmazásakor a jel spektrumát a  komplex amplitúdó függvény értékei adják meg. Ebben az esetben lehetőség van a komplex amplitúdók valós és képzetes részeinek elkülönítésére. A gyakorlatban a spektrumot a  függvény együtthatóinak abszolút értékeiből ábrázolják, és ezt teljesítmény spektrumnak nevezik.

Fourier 1807-ben publikált dolgozatában a hőmérséklet eloszlást közelítette szinusz függvényekkel. J.L. Lagrange véleménye szerint a „sarkot” nem lehet szinuszokkal közelíteni, ezért a dolgozatot visszautasították. Amint az alábbi példa mutatja Lagrange-nak egyáltalán nem volt igaza.

A négyszög jel Fourier sora

Az alábbi, 22. ábrán a négyszögjel és annak spektruma, az animáció linkre kattintva pedig a sorfejtés folyamata látható.

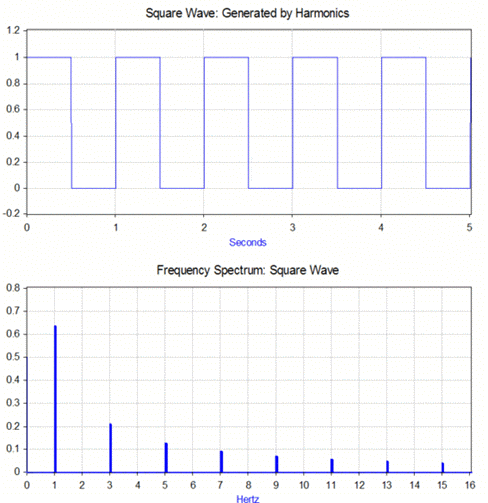
1. ábra Animáció a négyszögjel előállításához [6].

További animációkat az alábbi angol nyelvű oldalon találhat az olvasó.

Az elméletet azóta kiterjesztették nem periodikus függvényekre, valamint diszkrét idejű és értékkészletű és függvényekre is.

Fouriernek ez a felfedezése hatalmas jelentőséggel bír a jelfeldolgozásban, ugyanis lehetővé teszi, hogy bármilyen jelet a nagyon jól ismert szinusz és koszinusz függvényekkel közelítsünk. Ráadásul a jelfeldolgozás szempontjából további előny, hogy a szinuszos jelet egy lineáris rendszeren átengedve a kapott jel is szinuszos lesz, csak a fázisában, illetve amplitúdójában különbözhet, frekvenciájában nem.