A termelési függvény
A termelési függvény a felhasznált erőforrások (input) és a velük – maximálisan, azaz legtermelékenyebb felhasználásuk mellett – előállítható termékmennyiség (output) közötti kapcsolatot írja le. A termelési tényezőknek általában négy csoportját különböztetjük meg. Ezek: a) munkaerő (L), b) a termelésbe bevont természeti erőforrások (A), például a föld vagy egy művelés alatt álló bánya, c) az ún. tőkejavak (K), amelyek termelt termelési tényezők (eszközök, gépek, ingatlanok stb.), s végül d) a vállalkozói készség (E), maga a vállalkozó, aki nem közvetlenül vesz részt a termelésben, hanem a többi termelési tényező koordinálását látja el. A termelési függvényt általánosan a következő formában írhatjuk fel:
q = f(L, A, K, E), ahol L stb. az egyes tényezőfajták lehetséges mennyiségeit, q pedig az elképzelhető tényezőkombinációkkal előállítható maximális kibocsátásokat jelöli. Legyen most a termelési függvény algebrai alakja:
![]()
ahol L a felhasznált munka mennyiségét jelöli. Az egyéb tényezőket, például gépek, anyagok, energia és más termelési tényezők, változatlannak vesszük. Más néven ez egy rövid távú termelési függvény, s ezzel arra utalunk, hogy bár van olyan termelési tényező – jelen esetben a munka (L) –, aminek változtatásával a vállalat képes alkalmazkodni a piaci helyzet változásaihoz, de van vagy vannak olyan input-elemek is (jellemzően a tőkejavak), amelyek ilyen időtávon belül nem változtathatók meg. Hosszú távon – definíció szerint – minden felhasznált tényező mennyisége változhat.
Ez a függvény egy olyan termelési technológiát reprezentál, ahol a termelés megegyezik a felhasznált munkamennyiség (mondjuk: fő) négyzetgyökének százszorosával. A kibocsátást (q, egészre kerekítve) a felhasznált munkamennyiség (létszám) néhány értékére az alábbi táblázat második oszlopában találjuk.
2.1 táblázat: Termelési és költségfüggvények
| a dolgozók száma (L) | kibocsátás (q) | a munka határterméke | állandó költség | munkaköltség | összköltség |
| 0 | 0 | -- | 1000 | 0 | 1000 |
| 2 | 141 | 41 | 1000 | 200 | 1200 |
| 3 | 173 | 32 | 1000 | 300 | 1300 |
| 4 | 200 | 27 | 1000 | 400 | 1400 |
| 5 | 224 | 24 | 1000 | 500 | 1500 |
| 6 | 245 | 21 | 1000 | 600 | 1600 |
| 7 | 264 | 19 | 1000 | 700 | 1700 |
A harmadik oszlop a munka határtermékét tartalmazza. A közgazdaságtan egyik alapelve szerint a racionális emberek marginális változásokban gondolkoznak. A termelési tényezők, jelen esetben a munka határterméke (Marginal Product – MPL) egy ilyen „marginális változás”. Azt mutatja meg, hogy mennyivel nő a termelés, ha – ceteris paribus – egységnyivel növeljük a munkafelhasználást.
Képletben:

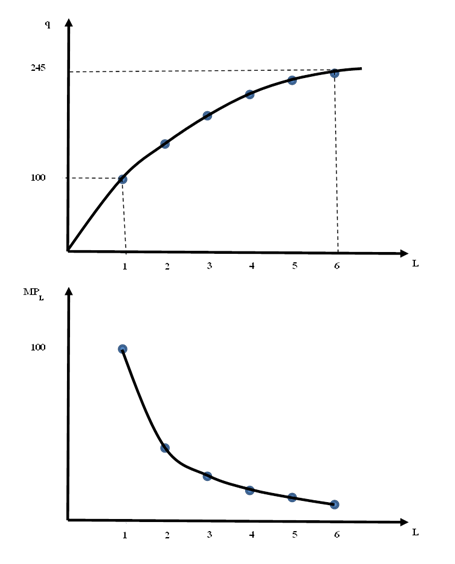
Látjuk, hogy ha a dolgozók száma példánkban egyről kettőre nő, a termelés 41-gyel, ha kettőről háromra, akkor 32-vel, ha háromról négyre, akkor 27-tel lesz több. Ez egy hihető tulajdonsága termelési függvényünknek (a termelési technológiának). Ezek szerint, ha a munka újabb és újabb egységeit rendeljük a többi – változatlan mennyiségű – termelési tényezőhöz, akkor a munka termelésnövelő hatása (a határtermék) egyre kisebb. A közgazdászok ezt a jelenséget a csökkenő hozadék elvének nevezik. A határtermék nem más, mint a termelési függvény meredeksége. Nézzük meg ezt grafikonokon is! A felső ábráról azt olvashatjuk le, hogy a munka-tényező (L) különböző mennyiségeit változatlan mennyiségű egyéb tényezővel kombinálva mekkora termelési szintek (q) érhetők el. Az alsó ábra a munka újabb és újabb egységeinek termelésnövelő képességét, a határterméket jeleníti meg.
2.1. ábra: Teljes termelés és a munka határterméke
A 2.1. táblázat további oszlopai a többi tényező költségeit (állandó költség – Fixed Cost), a változó tényező (itt: munka) költségeit (változó költség – Variable Cost), illetve a termelés teljes költségét tartalmazzák. Ezek az adatok azonban még nem igazítják el a vállalakozót, amikor arról kell döntenie például, hogy hány munkást alkalmazzon. Nézzük a következő táblázatot!
2.2. táblázat: Költségfüggvények
| kibocsátás (q) | összköltség (TC) | állandó költség (FC) | munka-költség (VC) | átlagos változó költség (AVC) | átlagos fix költség (AFC) | átlag-költség (AC) | határ-költség (MC) |
| 0 | 1000 | 1000 | 0 | - | - | - | |
| 100 | 1100 | 1000 | 100 | 1,000 | 10,000 | 11,000 | 1,000 |
| 141 | 1200 | 1000 | 200 | 1,418 | 7,092 | 8,511 | 2,439 |
| 173 | 1300 | 1000 | 300 | 1,734 | 5,780 | 7,514 | 3,125 |
| 200 | 1400 | 1000 | 400 | 2,000 | 5,000 | 7,000 | 3,704 |
| 224 | 1500 | 1000 | 500 | 2,232 | 4,464 | 6,696 | 4,167 |
| 245 | 1600 | 1000 | 600 | 2,449 | 4,082 | 6,531 | 4,762 |
| 264 | 1700 | 1000 | 700 | 2,652 | 3,788 | 6,440 | 5,263 |
Az utolsó előtti oszlop adatai (átlagköltség – Average Cost) azt mutatják meg, hogy átlagosan mennyibe kerül elkészíteni egy-egy terméket, az utolsó oszlopban pedig azt látjuk, hogy egy újabb termék elkészítése mennyivel növeli a költségeket (határköltség – Marginal Cost). Bár első pillanatra úgy tűnhet, hogy ezekre a kérdésekre ugyanaz a válasz, valójában ez nem így van. Az átlagköltségnek egyfelől része a – kibocsátás növekedésével egyre csökkenő – átlagos fix költség (AFC), ami a határköltségre nincs hatással, másrészt az átlagköltség tükrözi a korábbi határköltségeket is, míg a határköltség csak az utoljára előállított termékegység költségvonzatát mutatja. Képletben:

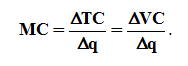
A termelési döntésekben mindkét költségkategóriának fontos szerepe van, de – mint látni fogjuk – a szerepük eltérő. A határköltség példánkban minden kibocsátási szinten növekvő a csökkenő határtermék miatt, az átlagköltség változásában azonban előbb a csökkenő átlagos fix költség dominál, ekkor AC csökken, s csak később válik a növekvő átlagos változó költség hatása meghatározóvá. Az MC- és az AVC-görbe így mindenütt emelkedő, az AC-görbe viszont U-alakú. Az AC minimumát eredményező q* kibocsátást technikailag hatékony kibocsátási szintnek nevezzük, a termelés egy egységére jutó költség ekkor a legkisebb. Ez azonban nem jelenti azt, hogy a vállalatnak ezt a termelési szintet célszerű választania, hiszen a vállalat célja nem az átlagköltség minimalizálása, hanem a profit maximalizálása.
A költségfüggvények tipikus „együttállását” a 2.2. ábra mutatja. Matematikailag itt nem bizonyítjuk, bár anélkül is könnyen belátható – hiszen amíg a határköltség kisebb, mint az átlagos költség, addig utóbbi csökken, ellenkező esetben nő –, hogy a határköltség-görbe mind az AVC-t, mind az AC-t azok minimumában metszi (példánkban az AVC-t nem metszi MC, de a közös pontjuk az AVC minimumában van).
2.2. ábra: Tipikus költségfüggvények
