Az epipoláris geometria a fényképek alapján történő térbeli rekonstrukció és távolságmérés matematikai eszköze. Az epipoláris geometria sztereó képpárok közötti kapocslatot ír le.

Tekintsünk egy térbeli pontot és két képsíkot, a bal és a jobb kamera képsíkjait. Az  pont képe a bal kamera képsíkján , a jobb kamera képsíkján . Jelölje bal és a jobb kamera középpontját rendre  és .
A kamera középpontokat összekötő egyenes a bázisegyenes (angolul baseline). Az térbeli pont és a két kamera középpont által meghatározott sík az epipoláris sík. A képsíkok és az epilpoláris sík metszetei az epipoláris egyenesek. Az alábbi ábrán látható ezek ábrázolása.

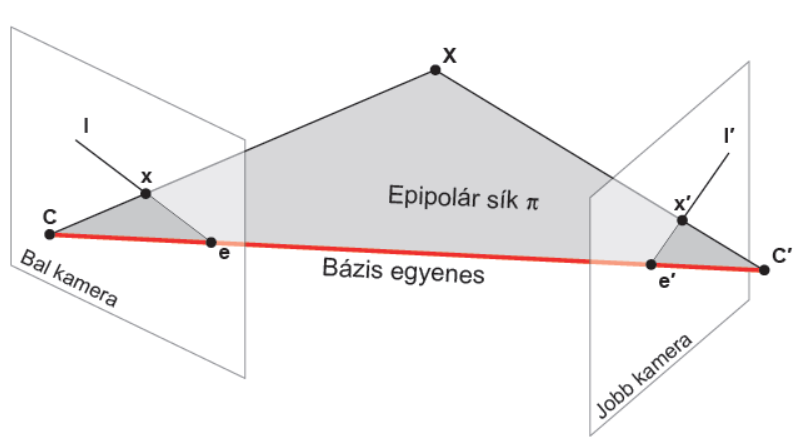
A célunk az, hogy kapcsolatot keressünk a két kamera képe között. A bal kamera  középpontját és az térbeli pontot összekötő vetítősugár képe a jobb kamera síkjában az egyenesként látszik, amelyet epipoláris egyenesnek hívunk. Mindegyik vetítősugár képe a másik kamerában egy egyenesként látszódnak, és ezek az epipoláris egyenesek egy pontban, az epipolban metszik egymást (a fenti ábrán ezeket és jelöli). Másrészről pedig az epipolok a bázisegyenes és képsíkok metszéspontjai is. Tehát a bal kamera képsíkjának minden pontjázhoz a jobb kamera képsíkján egy epipoláris egyenes tartozik, amelyek egyetlen pontban, az  epipolban metszik egymást. Ezt a kapcsolat az  fundamentális mátrixszal írható le az alábbi módon:

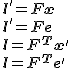
A fundamentális mátrix mérete 3×3, rangja 2. Az is igaz továbbá, hogy minden  rajta van az egyenesen, ezért vagyis  . A fenti egyenlőségek minden pontpár esetén fennálnak, ezért egy pontpárra az kiszámolható az alábbi módon:

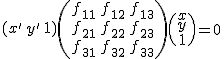
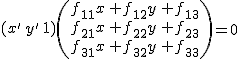
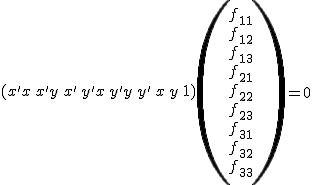
Ha n pontpárunk van, akkor a következő egyenletrendszert kell megoldani:

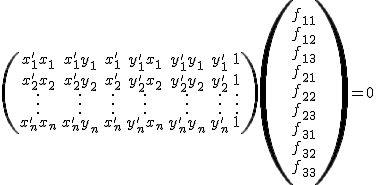
Legalább 8 pontmegfeleltetés szükséges. Ha rangja nagyobb mint 8, akkor túlhatározott egyenletrendszert kapunk, amelynél a legkisebb négyzetes hiba meghatározásával lehet megkapni a megoldást.  kiszámításához a normalizált 8 pontos algoritmust használjuk (lásd előadásanyag).

Epipólusok meghatározása

Mivel az epipólus valamennyi epipoláris egyenesen rajta van, ezért

Az epipólusokat az fundamentális mátrix SVD felbontásával kapjuk

• az  epipólus a 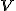nullla szinguláris értékének megfelelő oszlopvektora lesz
• az 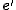 epipólus az 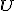nullla szinguláris értékének megfelelő oszlopvektora lesz

Esszenciális mátrix

Amennyiben ismerjük a kalibrációs mátrixot, akkor

• inverzével megszorozva a képpontokat normalizált koordinátákat kapunk:
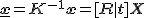
• inverzével megszorozva a kamera mátrixot, normalizált kameramátrixot kapunk:

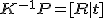
Tekintsünk egy normalizált kamera párt

A kamera párnak megfelelő fundamentális mátrixot esszenciális mátrixnak nevezzük:

Továbbra is teljesül:

Az és között a kapcsolat:

Négy megoldás lehetséges, de csak egy lesz jó, ahol a két kamera egy irányba néz.

Rektifikáció

A képek rektifikációja az epipoláris geometrián alapszik. A rektifikáció során azt a transzformációt (vagy transzformációkat) keressük, amely a képsíkokat egy síkba transzformálja. A rektifikáció után a bal és jobb kamera képe egy síkba kerül, továbbá a két képen az egymásnak megfelelő pontok ugyanazon pixelsorba kerülnek. A rektifikáció során felhasználjuk a pontpárokat, valamint a fundamanetális mátrixot. Mivel a rektifikáció során az egymásnak megfelelő képpontok egy pixelsorra kerülnek, így gyakorlatilag az epipoláris egyenesek párhuzamosak lesznek mindkét képen.