A mechanikai hullámok jellemzői

A hullámokat több szempont szerint osztályozhatjuk. Ha a közegben mechanikai állapotváltozások terjednek, akkor mechanikai hullámról, ha pedig elektromágneses természetű zavar terjed, akkor elektromágneses hullámról  beszélünk. A mechanikai hullámok terjedéséhez valamilyen rugalmas közegre van szükség, szemben az elektromágneses hullámokkal, amelyek vákuumban is képesek terjedni.

Aszerint, hogy a tér hány dimenziója mentén terjed a hullám, megkülönböztethetünk egydimenziós hullámokat (pl. rezgő gumikötél), kétdimenziós hullámokat (pl. a levegőben terjedő vízhullámok) és háromdimenziós hullámokat (pl. a levegőben terjedő lökéshullámok egy robbanás körül). A rezgés iránya szerint különbséget teszünk transzverzális és longitudinális hullámok között. A transzverzális hullámok terjedési iránya a rezgési irányra merőleges (ilyenek például a húron terjedő hullámok vagy az elektromágneses hullámok). A longitudinális hullámok terjedési iránya ezzel szemben párhuzamos a rezgési iránnyal (ilyen például a legtöbb hanghullám). Bizonyos transzverzális hullámok a terjedés irányára merőlegesen egyetlen kiválasztott síkban rezegnek, az ilyen hullámokat polarizált hullámoknak nevezzük.

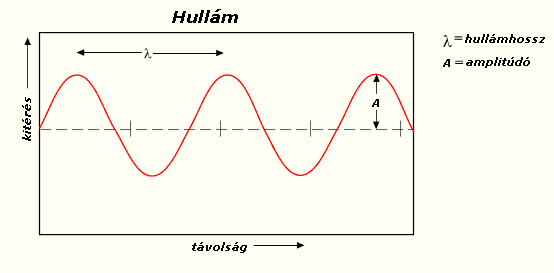
A harmonikus hullámok terjedéséül szolgáló közeg egyes pontjaiban a részecskék – mechanikai hullám esetén – harmonikus rezgőmozgást végeznek. Mivel ezáltal szoros kapcsolat van a harmonikus rezgések és hullámok között, a harmonikus hullámok jellemzéséhez is használjuk a harmonikus rezgések témaköréből ismert alapmennyiségeket (amplitúdó, periódusidő, frekvencia, körfrekvencia, kezdőfázis stb.). Ezt egészíti ki egy további, a térbeli periodicitást jellemző mennyiség, a hullámhossz. A hullámhossz a hullám két azonos fázisú szomszédos pontja (például két szomszédos maximuma vagy minimuma) közötti távolság valamely rögzített időpillanatban. A hullámhossz jele a λ, SI-mértékegysége a m (méter). Különösen a spektroszkópia területén gyakran alkalmazzák a k hullámszámot, amely a hullámhossz reciprokának 2π-szerese:

\[k \equiv 2\pi /\lambda\]

(A hullámszám más definíció szerint közvetlenül a hullámhossz reciproka, és megkülönböztetésképp az előző mennyiséget körhullámszámnak nevezik.) A hullámszám 1/hosszúság dimenziójú, SI-mértékegysége az 1/méter.

A mechanikai hullámok terjedési sebességét a közeg mechanikai tulajdonságai (sűrűség, rugalmassági jellemzők), az elektromágneses hullámok terjedési sebességét pedig a közeg törésmutatója határozza meg. A hullám adott közegbeli c terjedési sebessége, λ hullámhossza, k hullámszáma, f frekvenciája, T periódusideje és ω körfrekvenciája között a következő összefüggések vannak érvényben:

\[c=\lambda \cdot f = \frac{\lambda}{T}=\frac{\lambda \cdot \omega}{2 \pi}=\frac{\omega}{k}\]

A fenti gondolatmenet alapján egy A amplitúdójú, ω körfrekvenciájú és φ_o kezdőfázisú harmonikus rezgés hatására kialakuló, a közegben c sebességgel terjedő (egydimenziós) harmonikus hullám rezgésállapotát („kitérését”) a

\[\Psi \left ( x, t \right )=A \cdot \sin \left [ \omega \left ( t-\frac{x}{c} \right ) + \varphi_0 \right ]\]

hullámegyenlet írja le.

A hullám I intenzitását a hullámban egységnyi idő alatt, egységnyi felületen keresztül szállított energiával definiáljuk:

\[I=\frac{E}{A \cdot t}=\frac{P}{A}.\]

ahol E a hullámnyaláb energiája, amely az A felületen halad át t idő alatt, és P a teljesítmény. Az intenzitás teljesítmény/felület dimenziójú, SI-mértékegysége a W/m². A hullámnyaláb intenzitása egyenesen arányos a hullám amplitúdójának és frekvenciájának négyzetével, és amint arra a fenti egyenlet rámutat, a hullámnyaláb átlagos intenzitása a nyaláb teljes teljesítményének és keresztmetszetének hányadosaként számolható ki.