A hullámterjedés során fellépő jelenségek

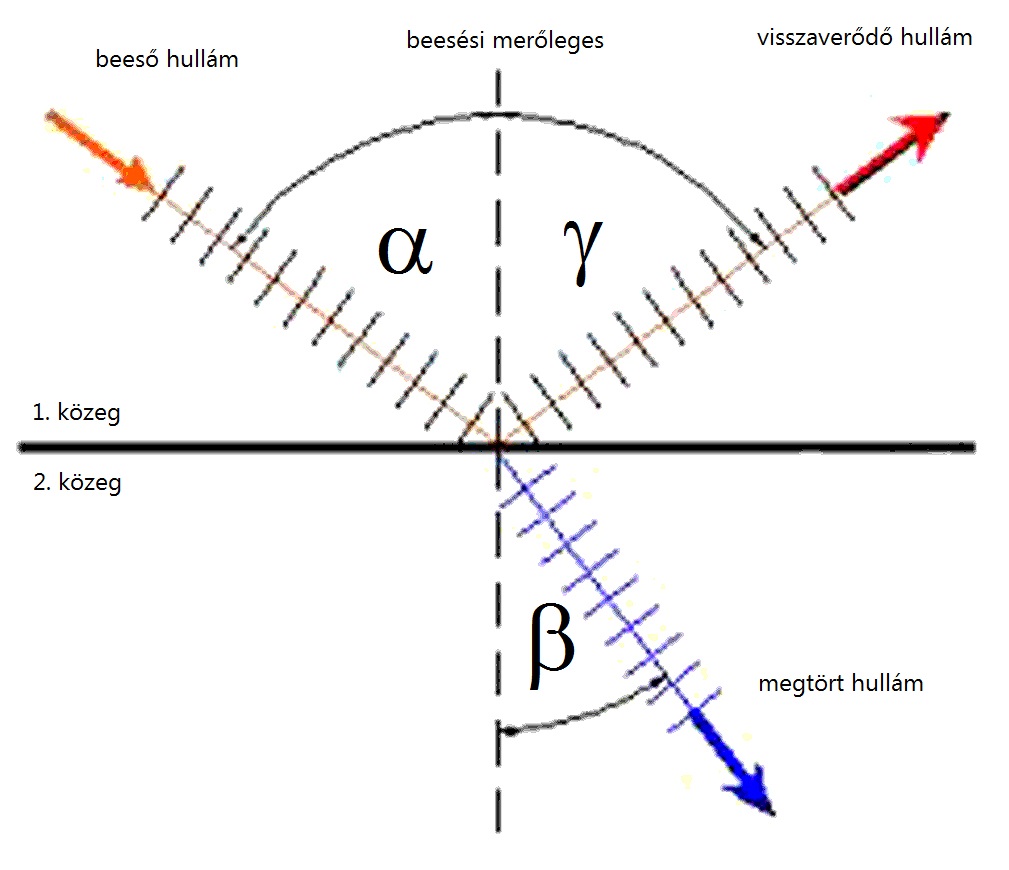
Ha egy hullám terjedés közben olyan közegek határfelületéhez érkezik, amelyekben a hullámterjedési sebesség különböző, a közeghatárról a hullám egy része visszaverődik, a visszamaradó rész pedig megtörve folytatja útját a második közegben (a szóródástól itt és a továbbiakban eltekintünk).

Visszaverődés során a közeghatárt elérő hullám nem hatol be a közeghatár túloldalán lévő közegbe, hanem a következő törvényszerűségek szerint változtatja meg a terjedési irányát:

• a visszaverődő hullám a beeső hullám és a beesési merőleges (a határfelületre a hullám beérkezési pontjában állított merőleges) síkjában halad tovább;
• a γ visszaverődési szög egyenlő az α beesési szöggel: α = γ.

Beesési szögnek a beeső hullám terjedési iránya és a beesési merőleges által bezárt szöget, visszaverődési szögnek pedig a visszaverődött hullám terjedési iránya és a beesési merőleges által bezárt szöget nevezzük.

Törés esetén a hullám belép a közeghatár túloldalán lévő közegbe, miközben a terjedési iránya az alábbiak szerint változik meg:

• a megtört hullám a beeső hullám és a beesési merőleges síkjában halad tovább;
• az α beesési szög szinuszának és a β törési szög szinuszának hányadosa a két közegre jellemző állandó, az ún. n_2,1 (relatív) törésmutató:

\[\frac{\sin \alpha }{\sin \beta }=n_{2,1}\equiv \frac{c_1}{c_2}.\]

A fenti egyenletet Snellius–Descartes-törvénynek nevezik. A törési szög a megtört hullám terjedési iránya és a beesési merőleges által bezárt szög, a törésmutató pedig az adott hullám első és második közegben mérhető c₁ és c₂ terjedési sebességeinek hányadosa. A törésmutató különösen az optikában bír nagy jelentőséggel.

Hullámok találkozásakor az amplitúdók a hullámtér minden pontjában előjelesen összeadódnak, így a hullámok erősíthetik, illetve gyengíthetik (sőt, akár ki is olthatják) egymást. Ezt a jelenséget interferenciának nevezzük. Két azonos polarizációjú és frekvenciájú hullám interferenciája matematikailag a találkozó hullámok által keltett rezgések pontonkénti összetevésével írható le. Interferencia során az interferáló hullámok eredő amplitúdóját vagy intenzitását észleljük. Amennyiben a lenti megjegyzésben definiált interferenciatag pozitív, akkor erősítésről, ellenkező esetben gyengítésről beszélünk. Az interferenciára képes forrásokat koherens forrásoknak nevezzük. Az interferencia szép példája a vízfelszínen találkozó hullámok által kialakított mintázat.

Diffrakcióról (elhajlásról) akkor beszélünk, amikor a hullámok a hullámhosszal összemérhető nagyságú akadályba vagy nyílásba ütköznek, és – az interferencia törvényszerűségeit követve – eredeti terjedési irányuktól eltérve haladnak tovább, „elhajlanak”. A diffrakció a Huygens–Fresnel-elv alapján tárgyalható, amelynek tézisei a következőképp fogalmazhatók meg:

1. A hullámfelület minden pontja elemi gömbhullámok kiindulópontja.
2. Egy adott pontban tapasztalható hatást az elemi hullámok interferenciája alakítja ki.

A polarizáció a transzverzális hullámok rezgési síkjának rendezetlenségét írja le. Ha ez a sík gyorsan és rendezetlenül változik, akkor polarizálatlan hullámról beszélünk. Amennyiben a polarizáció síkja térben állandó, a hullámot lineáris polarizáltnak nevezzük, ha pedig ez a sík állandó szögsebességgel mozog, akkor a hullámot elliptikusan vagy cirkulárisan polarizáltként írjuk le.