Az adatmodellezes és a relációs algebra

Az adatmodell


Egy adatmodell célja a való világról szerzett és feldolgozott tapasztalataink számítógépek segítségével azok eltárolásához megfelelő kerettel tudjon szolgálni, biztosítsa az eltárolt adatokra való rákereshetőség lehetőségét. Minden adatmodellhez társítunk egy sémát, ami az adatmodell formai és tartalmi leírását adja. Attól függően, hogy az adatmodell elemeiből milyen módon hozzuk létre az adatmodell szerkezetét, az alábbi modellekről beszélhetünk:

  • Relációs

  • Objektumorientál

  • Hálós

  • Hiearchikus

Az adatmodellezés


Az adatmodellezés definíció szerint az adatbázis szerkezetének megtervezését jelenti, melynek menetei a következőek: a koncepcionális, a logikai, és a fizikai adatmodell elkészítése a kapcsolódó leírásokkal, illetve adatmodell diagramokkal:

  • Koncepcionális adatmodell (EK modell): olyan adatmodell, mely a valóságban megtalálható objektumok egyedi tulajdonságait, továbbá az egymáshoz való viszonyaikat oly módon képezi le fogalmi szintre (a megfelelő lényeges elemeket kiemelve), hogy a lehető legjobban tükrüzze vissza a valódi objektumokat és az egymáshoz való viszonyukat. Ezen modell tartalmazza az egyedeket, azok tulajdonságait, továbbá az kapcsolatait. Az adatok modelljét, és azok egymáshoz viszonyított relációját vizuálisan az Egyed-kapcsolat diagram mutatja meg.

  • Logikai adatmodell (ETK modell): olyan adatmodell, melyet a meglévő koncepcionális adatmodell leképzésével állítunk elő különböző szempontokat figyelembe véve (az adatbázis tervezési követelményei, az adatbáziskezelő rendszer típusa).

  • Fizikai adatmodell: olyan adatmodell, melyet a meglévő leképzésével állítunk elő különböző szempontokat figyelembe véve (a teljes fizikai megvalósítás terve).

Jelen tananyagban a továbbiakban a relációs adatmodellekkel fogunk foglalkozni.

A relációs adatmodell


A relációs adatmodell egyik legfontosabb koncepciója a matematikai reláció fogalma. Jegyezzünk meg, hogy a relációs adatmodell és a relációs adatbázis egymás szinonimái. Mint minden adatmodell, ez is egyrészt definiálja azokat a jellemző adatszerkezeteket, amelyeken dolgozik, illetve azokat a műveleteket, amelyek rajta értelmezettek. Ekkor az adatmodellt teljesnek nevezzük. Amíg az azonos tulajdonságtípusokkal rendelkező egyedeket egyedtípusokba soroljuk, addig az azonos jellemzőket leíró tulajdonságokat tulajdonságtípusokba csoportosítjuk. Minden egyes egyedet egy táblázat reprezentál, melynek oszlopai a tulajdonságok (attribútumok). A relációs adatmodell esetén az egyedek és az őket összekötő kapcsolataik helyett a tulajdonságokra helyeződik a hangsúly. Az egyed leírása a tulajdonságaival (attribútumaival) történik, továbbá a kapcsolatot az egyedek sémánál definiált, kulcs- illetve kapcsoló jellegű tulajdonságai megfelelő értékeinek megegyezésével hozható létre. A relációs adatmodell az alábbi elemekből épül fel:

  • Tábla: egy kétdimenziós táblázatnak felel meg, mely sorokból (rekordokból) és oszlopokból (mezőkből) állnak.

  • Rekord: A rekord a tábla egy sora, amely egy egyed összetartozó mezőértékek sorozatából áll.

  • Mező: A mező (attribútum) a tábla egy oszlopa, amelyben az egyedek tulajdonság értékek sorozatából áll.

  • Mezőérték: A tábla egy cellájában elhelyezkedő érték, amely az egyed tulajdonság-előfordulása.

A tábla egyedeinek azonosíthatóságát az elsődleges kulcs, a különböző egyedtípusok egyedei közötti kapcsolatok tárolását pedig az idegen kulcs valósítja meg.

A táblázatos leírással szemben támasztott követelmények


  • Minden tábla rendelkezzen egy egyedi azonosítóval (relációnév), melynek segítségével egyértelműen beazonosítható.

  • Minden oszlop (attribútum) rendelkezzen egy egyedi azonosítóval (attribútumnév), melynek segítségével egyértelműen beazonosítható.

  • Az adott oszlophoz tartozó mezőértékek kizárólag elemi szerkezetűek lehetnek, melyek formátuma és értéktartománya meghatározott.

A relációs algebra és alapfogalmai


A táblázatos leírás és az adatmanipulációkban leírt összefüggések alkotják az adatbáziskezelés adatmodelljét. Ahhoz, hogy magunkat (mint felhasználó) megérthessük a relációs adatbáziskezelővel (RDMS), szükséges feltétele egy szabványos adatlekérdező nyelv, egy adatdefiníciós nyelv, egy adatmanipulációs nyelv, és egy adatvezérlő nyelv. Szinte az összes relációs adatbáziskezelő nyelv a relációs algebrára épül. A relációs algebra az a fajta algebra, menyben az operandusok relációk (táblák) vagy változók, melyek relációkat képviselik. Az operátorok a relációs algebrában úgy vannak konstruálva, hogy képesek legyenek végrehajtani a legtöbb szükséges művelete a relációkon.

Definíció

Az operandusok olyan változók vagy értékek, melyekből új értékeket lehet generálni.

Definíció

Az operátorok olyan szimbólumok, melyek eljárásokat jelölnek új értékek generálására adott régi értékekből.

Ezzel a fajta algebrával kereső nyelvként tudjuk használni az adatbázisokban. Az egyik ilyen (az eddig felsorolt feltételeket teljesítő) szabványosított nyelv az SQL (Structured Query Language), melyet 1970-ben E.F. Codd foglalta össze a "A Relational Model of Data for Large Shared Data Banks" című tanulmányába [15]. A relációs algebrai műveletek mindegyike minden esetben relációkon értelmezett. Általában az algebrai (lekérdező-jellegű) műveletek nem változtatják meg az operandusként megadott relációkat (csupán olvassák azokat). Az eredmény egy teljesen új, önálló reláció lesz. Ezeket tehát tehát reláció transzformációnak nevezzük, melyek paraméter-relációkat leképezik egy eredmény relációba. Ez azt jelenti, hogy a bemenő operandusai relációk lehetnek, melyekkel az alábbi műveletek végezhetőek az adatokon: lekérdezés, módosítás, felvétel, törlés. Azokat az műveleteket, melyek egy paraméter-relációt tartalmaznak unárisnak, amelyek kettőt, azokat binárisnak nevezzük. A műveleteket elemi operátorokból (unió ,különbség, átnevezés, vetítés, kiválasztás, Descartes-szorzat) származtatjuk. Ezek közül bármelyiket elhagyva az összetett műveletek (metszet, kapcsolás) nem fejezhető ki. A művelek az alábbi négy típusba csoportosíthatóak:

  • Az első típusú műveletek a relációkon (mint halmazokon) végeznek halmazalgebrai műveleteket.

  • A második típusú műveletek a reláción (mint táblán) hajtanak végre valamilyen (oszlop, sor) transzformációt.

  • A harmadik típusú műveletek az előző két típus tulajdonságait ötvözik.

  • A negyedik típusú műveletek osztályozó szerepet töltenek be, melyek a paraméter-reláció valamely tulajdonságú sorait helyettesítik egyetlen sorral. Jelen tananyagban ezen műveletek nem kerülnek kifejtésre.

Ezek után következzen néhány alafogalom matematikai megfogalmazása a relációs adatmodellel kapcsoltban:

Definíció

Az adatbázis egy halmaz, melynek elemei az attribútumok és rendelkezik egy egyedi azonosítóval (séma név). Jelölése a következő: , ahol a séma neve, az adatbázis n-dik attribútuma.

Definíció

Az attribútum egy halmaz, melynek elemei a mezőértékek és rendelkezik egy egyedi azonosítóval (attribútum név). Az attribútum j-edik elemét -vel jelöljük.

Definíció

Az halmazok Descartes-szorzata az a halmaz, melynek elemei az olyan rendezett "n-esek", ahol az , az , ... , az halmaznak az eleme, s mely az összes ily módon létrehozható rendezett "n-est" tartalmazza.

Definíció

Relációsémának nevezünk egy attribútumhalmazt, amelyhez név tartozik: formálisan , ahol a relációséma neve, , pedig az attribútumhalmaza. Minden egyes attribútumhoz tartozik egy olyan értékkészlet, melyből felveheti az értékeit. Itt az i-edik attribútum értékkészletét jelöli. Az séma feletti tábla az alábbi módon írható le: . Röviden összefoglalva ez nem más, mint az értékkészletek Descates-szorzatainak részhalmaza (reláció). A reláció már egy konkrét (a sémára illeszkedő), kitöltött tábla, mely rendelkezik függésekkel.

Sématartó műveletek


Az ebbe a csoportba tartozó műveletek a paraméter-relációk sémáját egyáltalán nem változtatják meg. A bináris műveletek esetén viszont kompatibilitási követelményeknek kell megfelelni.

Reláció és attribútum átnevezés


Definíció

Legyen és két tetszőleges paraméter-reláció séma. Abban az esetben, ha a két séma neve megegyezik (netán előfordulnak olyan attribútumok, melynek nevei megegyeznek), akkor érdemes megkülönböztetni őket. A relációkat ekkor alias-névvel (másodlagos névvel) látjuk el. Ez nem jelenti azt, hogy az eredeti reláció nevét a szó szoros értelemben megváltoztatjuk, csupán elősegítjük az egy műveletben szereplő relációk megkülönböztetését. A relációkhoz hasonlóan a hozzájuk tartozó attribútumneveket elláthatjuk másodlagos attribútumnevekkel, elősegítve az egy műveletben szereplő attribútumok megkülönböztetését. Jelölése a következő: , ahol a b attribútum át lesz nevezve a-ra. Az attribútumok átnevezése helyett alternatíva az objektumorientáltság-elvéből kölcsönzött "dot-notation" szintaxissal egy paraméter-reláció séma egy tetszőleges attribútuma is elérhető (sémanév.attribútumnév). 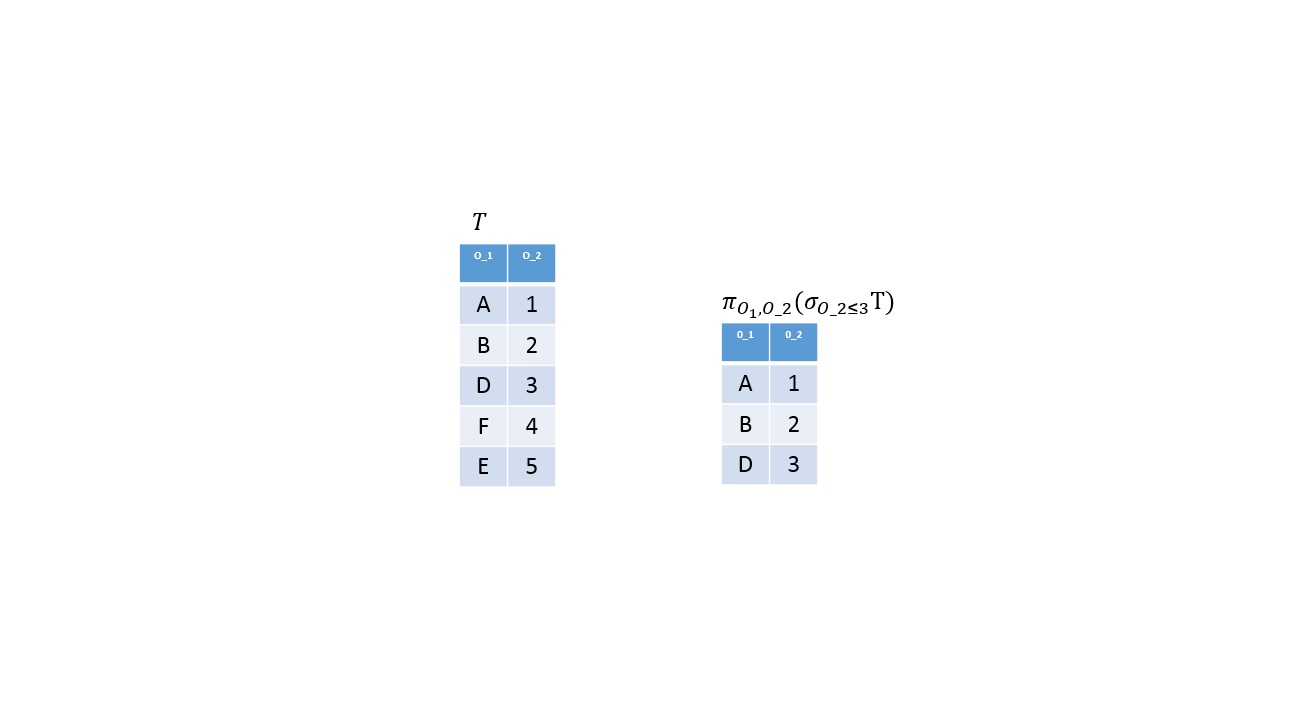Jelölése a következő: , ahol az a meghivatkozott attribútumai.

Kiválasztás


Definíció

Legyen egy tetszőleges paraméter-reláció séma és az feletti paraméter-reláció. A kiválasztás egy olyan egyoperandusú relációs algebrai művelet, mely kiválasztja a azon sorait, amelyek eleget tesznek egy feltételnek. Ahhoz, hogy meg tudjuk jeleníteni az eredmény-relációban, a vetítő operátort kell használnunk. Jelölése a következő: , ahol jelöli a feltételt ami meghatározza a kiválasztott rekordokat. Ha nem adunk meg konkrét attribútum nevet a vetítő operátornak, akkor alapértelmezetten az összes attribútumot levetíti. Jelölése a következő: .

Legyen paraméter-reláció séma és az feletti paraméter-reláció. Válasszuk ki (és vetítsük ki az összes attribútummal) azon rekordokat egy eredmény-relációba, melyek teljesítenek egy megadott feltételt: .

Kiválasztás

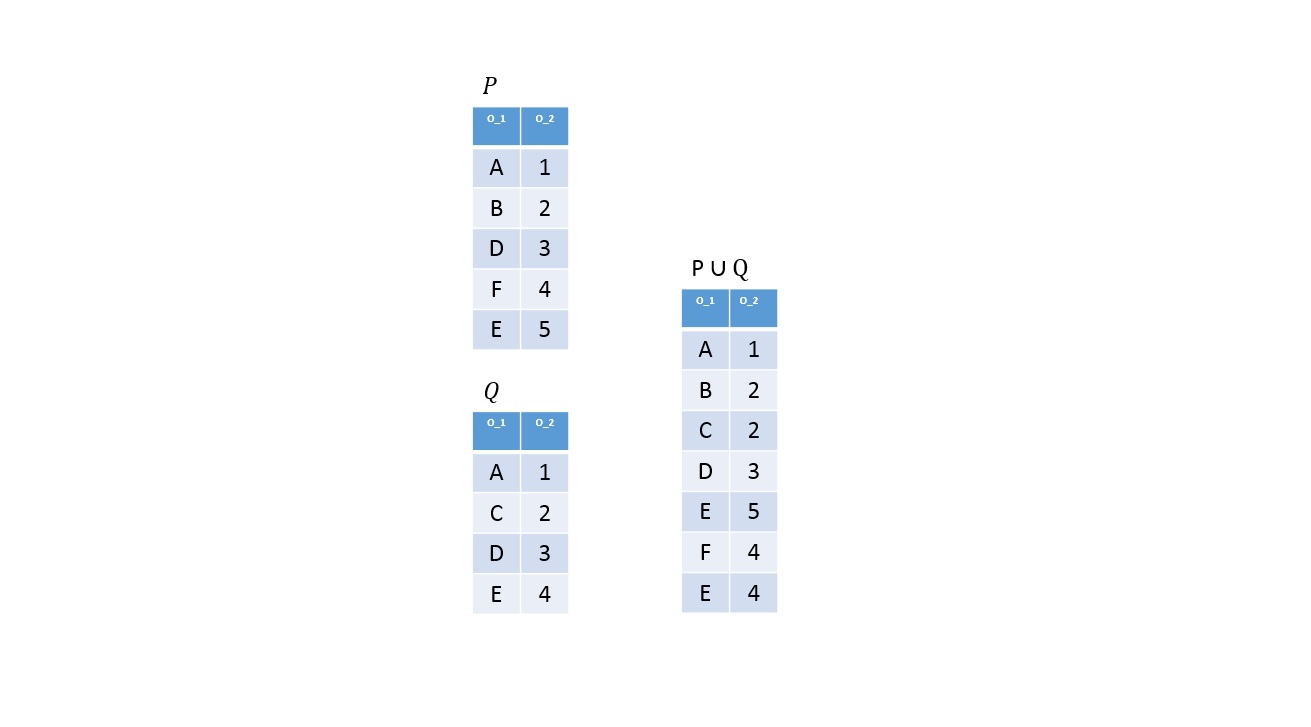
Unió


Definíció

Legyen és két tetszőleges paraméter-reláció séma, és az és feletti paraméter-relációk. Az unió egy olyan kétoperandusú halmaz és egyben relációs algebrai művelet, mely két vagy több azonos sémájú paraméter-reláció között végezhető el. Az eredmény-reláció tartalmazza azokat a sorokat, melyek a műveletbe bevont paraméter-relációk közül legalább egyben szerepelnek. Amennyiben ugyanaz a sor az egyesítendő relációk közül többen is szerepelne, akkor is csak egyszer szerepel az eredmény relációban. Jelölése a következő: .

Legyen és paraméter-reláció sémák, és az és feletti paraméter-relációk. Képezzük a két reláció unióját egy eredmény-relációba: .

Unió

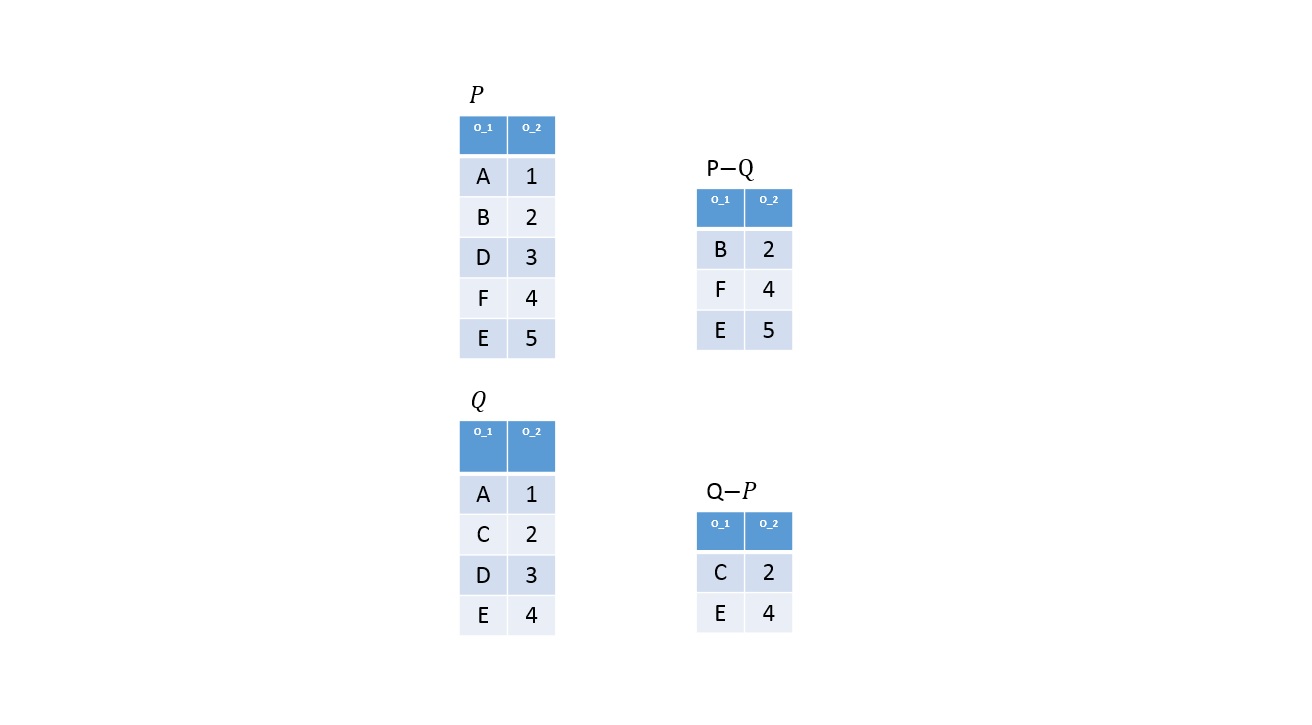
Különbség


Definíció

Legyen és két tetszőleges paraméter-reláció séma, és az és feletti paraméter-relációk. A különbség egy olyan kétoperandusú halmaz és egyben relációs algebrai művelet, mely két azonos sémájú paraméter-reláció között végezhető el. Az eredmény reláció csak azokat a sorokat tartalmazza, melyek a első relációban megtalálhatóak, viszont a másodikban nem. Jelölése a következő: . A különbség nem kommutatív művelet.

Legyen paraméter-reláció sémák, és az és feletti paraméter-relációk. Képezzük a két reláció különbségét egy eredmény-relációba: és .

Különbség

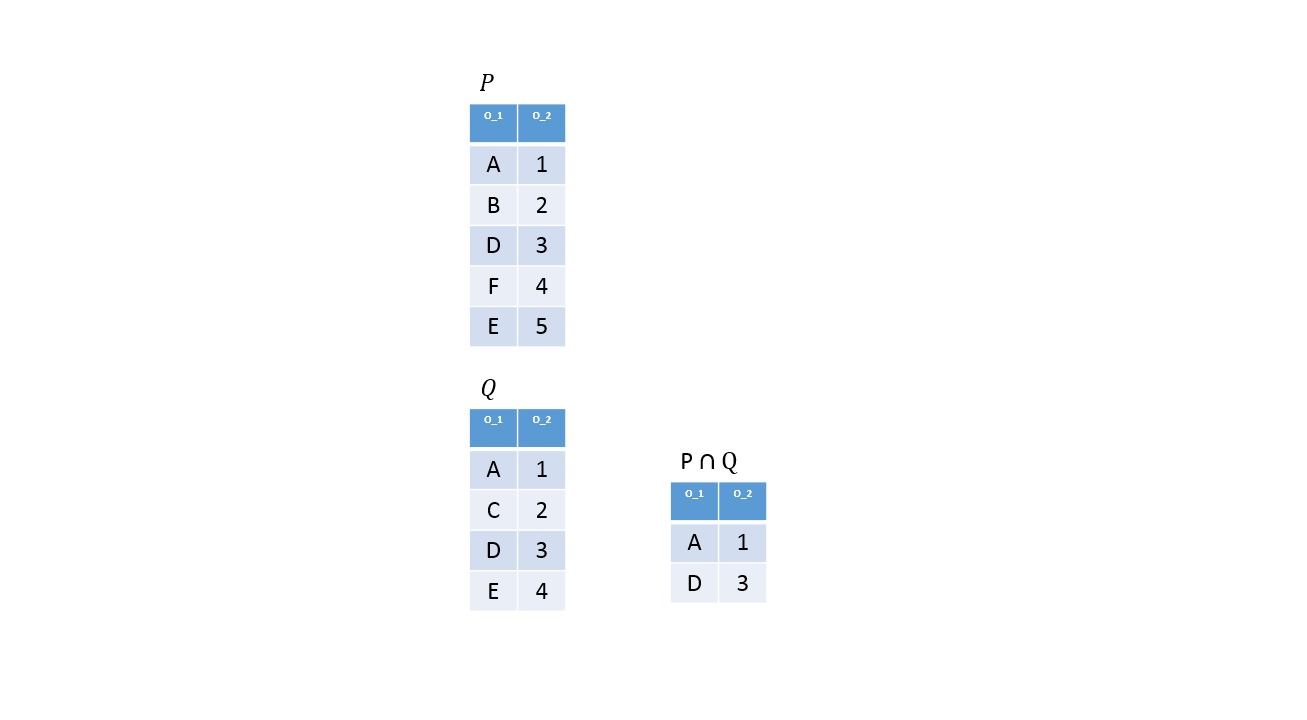
Metszet


Definíció

Legyen és két tetszőleges paraméter-reláció séma, és az és feletti paraméter-relációk. A metszet egy olyan kétoperandusú halmaz és egyben relációs algebrai művelet, mely vagy több azonos sémájú paraméter-reláció között végezhető el. Az eredmény reláció csak azokat a sorokat tartalmazza, melyek a műveletbe bevont relációk közül mindegyikben szerepelnek. Jelölése a következő: . A metszet műveletet származtatjuk: .

Legyen paraméter-reláció sémák, és az és feletti paraméter-relációk. Képezzük a két reláció metszetét egy eredmény-relációba: .

Metszet

Sémamódosító műveletek


Az ebbe a csoportba tartozó műveletek a paraméter-reláció sémákra való hattatásával az a eredmény-reláció sémája el fog térni.

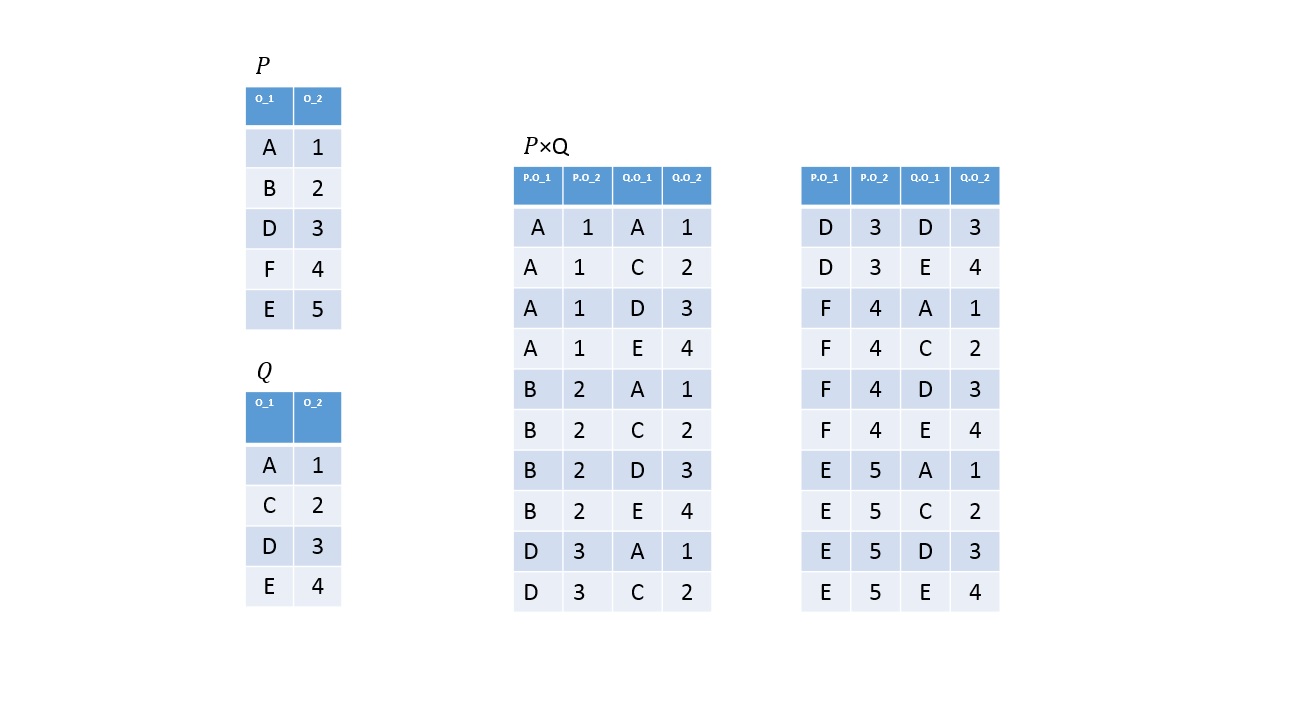
Descartes-szorzat


Definíció

Legyen és két tetszőleges paraméter-reláció séma és táblák , felett, ahol és az m-edik és n-edik attribútum értékkészletek. A Descartes-szorzat egy olyan kétoperandusú relációs algebrai művelet, mely olyan táblát eredményez, ahol minden sorát párosítunk minden sorával. Ha és paraméter-relációkban előfordulnak azonos nevű attribútumok, akkor meg kell különböztetni őket egy korábbi alfejezetben ismertetett techmikák valamelyikével (attribútum átnevezés, objektum-orientált hivatkozás).

Legyen paraméter-reláció sémák, és az és feletti paraméter-relációk. Képezzük a két reláció Descartes-szorzatát egy eredmény-relációba: .

Descartes szorzat

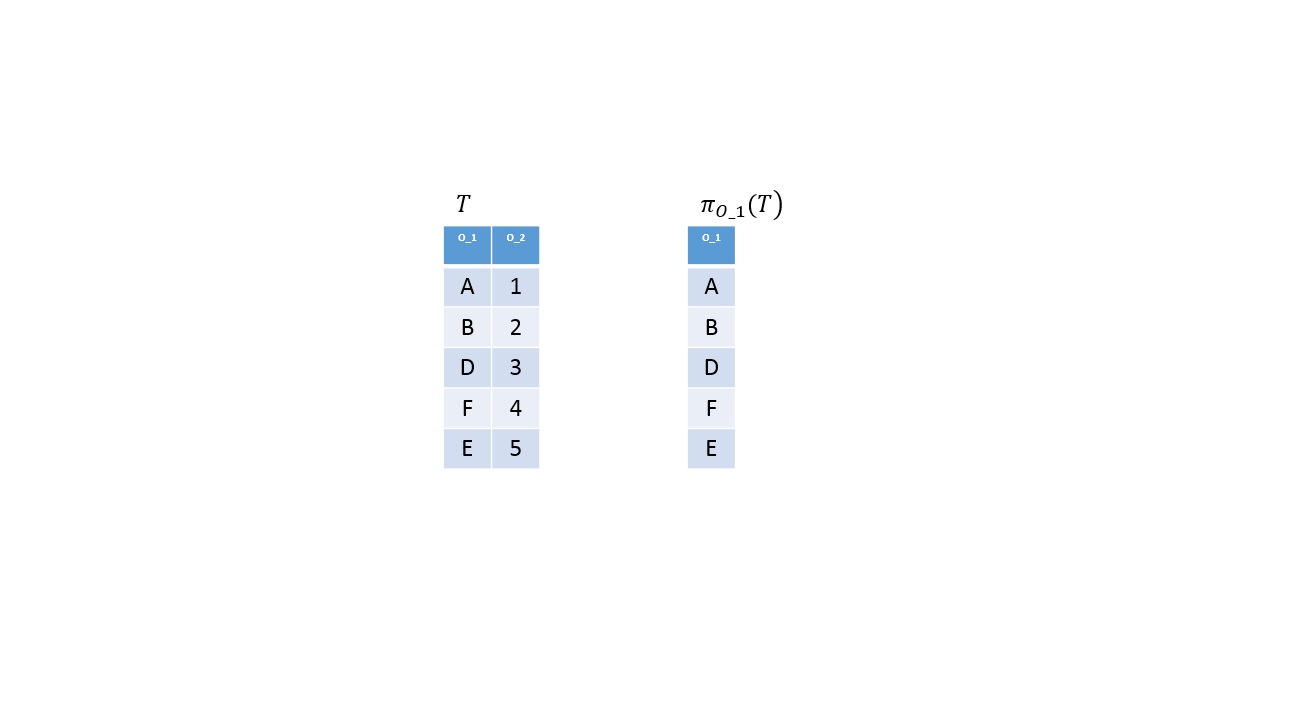
Vetítés


Definíció

Legyen egy tetszőleges paraméter-reláció séma, az feletti paraméter-reláció. A vetítés egy olyan egyoperandusú relációs algebrai művelet, mely egy adott paraméter-relációt vetít le egy megadott attribútum listára (melyből lesz az eredmény-reláció). Ha az paraméter-relációban előfordulnak azonos nevű attribútumok, akkor meg kell különböztetni őket egy korábbi alfejezetben ismertetett techmikák valamelyikével (attribútum átnevezés, objektum-orientált hivatkozás). .

Legyen paraméter-reláció séma, az feletti paraméter-reláció. Képezzük a vetített "változatát" egy eredmény-relációba: .

Projekció

Kapcsolás


A kapcsolás egy olyan kétoperandusú relációs algebrai művelet, mely két vagy több paraméter-relációt kapcsol össze (egy-egy attributum érték összehasonlításával). Megkülönböztetjük egymástól az alábbi kapcsolásokat.

  • Belső kapcsolás.

  • Külső kapcsolás.

Belső kapcsolás

A belső kapcsolás egy olyan kapcsolás, melynél azon sorok lesznek kiválasztva a paraméter-relációkból (és fognak képezni egy eredmény-relációt), melyek teljesítenek egy kívánt feltételt. Megkülönböztetjük egymástól az alábbi belső kapcsolásokat

  • Természetes kapcsolás.

  • Theta (általános) kapcsolás.

  • Egyenlő kapcsolás.

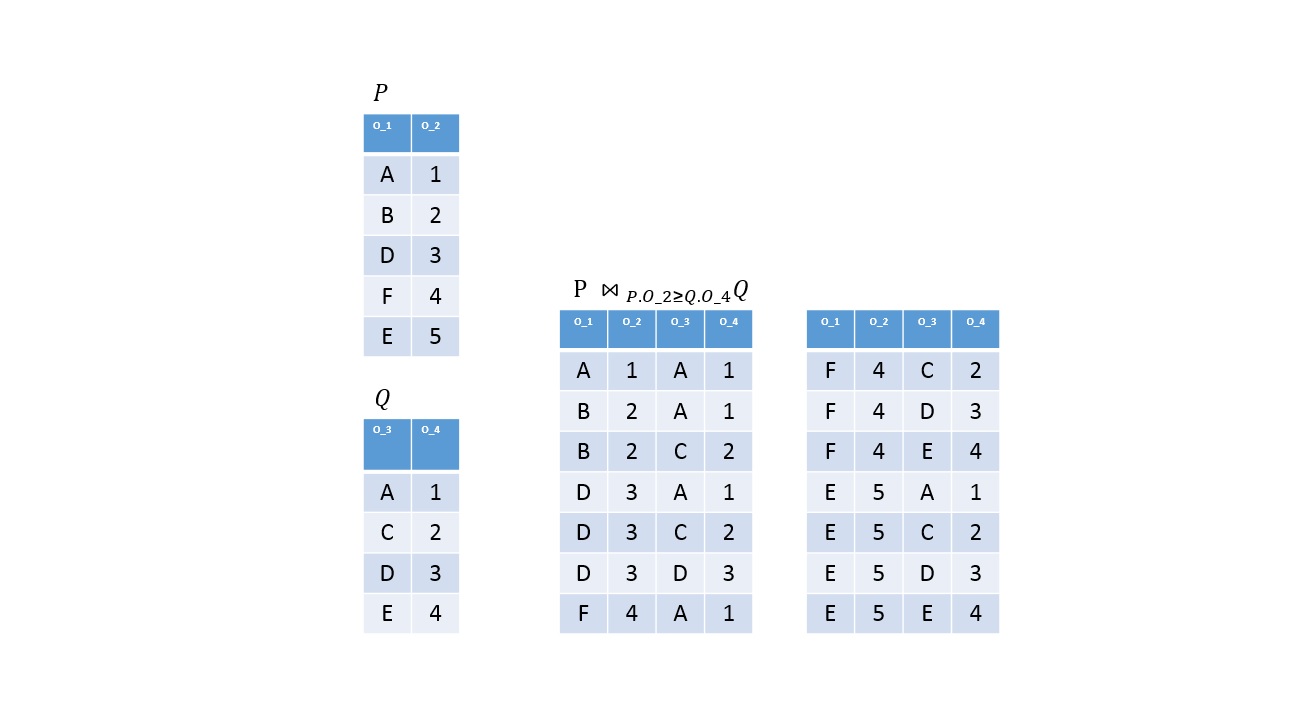
Theta kapcsolás

Definíció

Legyen és két tetszőleges paraméter-reláció séma, és az és relációsémák feletti paraméter-relációk. A theta kapcsolás egy olyan kétoperandusú relációs algebrai művelet, mely a két reláció Descartes-szorzatának azon sorait választja ki, melyben az adott oszlopok relációban vannak és eleget tesznek egy megadott feltételnek. Jelölése a következő: . A kapcsolás származtatott művelet: .

Legyen és két tetszőleges paraméter-reláció séma, és az és relációsémák feletti paraméter-relációk. Képezzük a két reláció theta kapcsolását egy eredmény-relációba egy megadott () feltétel mellett: .

Theta kapcsolás

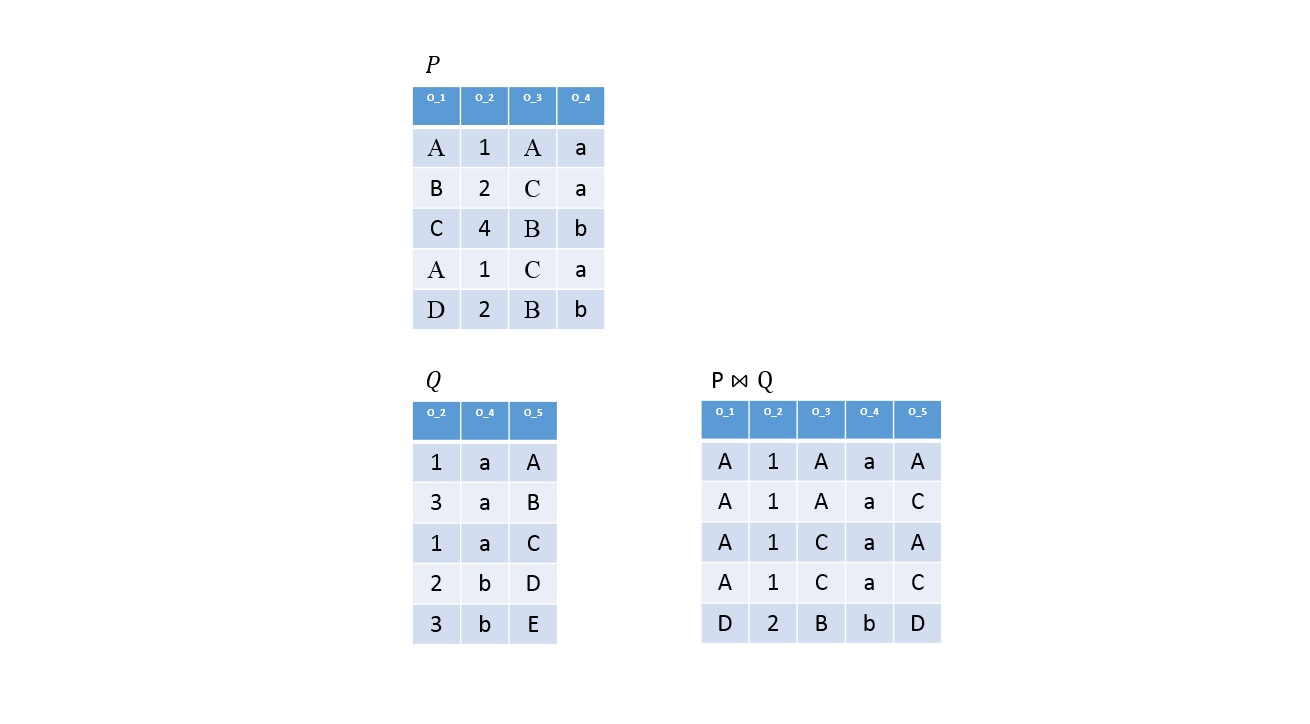
Természetes kapcsolás

Definíció

Legyen és két tetszőleges paraméter-reláció séma, és az és relációsémák feletti paraméter-relációk. Legyen és úgy, hogy: , , ahol és az attribútum halmazok. A természetes kapcsolás egy olyan kétoperandusú relációs algebrai művelet, mely az egyesítési feltétel a két paraméter-reláció azonos elnevezésű attribútumaira követeli meg az értékegyezőséget. Legyen egy egyesítési feltétel a következő: . Ahhoz, hogy eredmény-reláció a redundancia elkerülése végett a kapcsoló attribútumot csak egyszer tartalmazza, a vetítő operátort kell használnunk az alábbi módon: . A természetes kapcsolás jelölése a következő: . A természetes kapcsolás származtatott művelet: .

Legyen és paraméter-reláció sémák, és az és feletti paraméter-relációk. Képezzük a két reláció természetes kapcsolását egy eredmény-relációba: .

Természetes kapcsolás

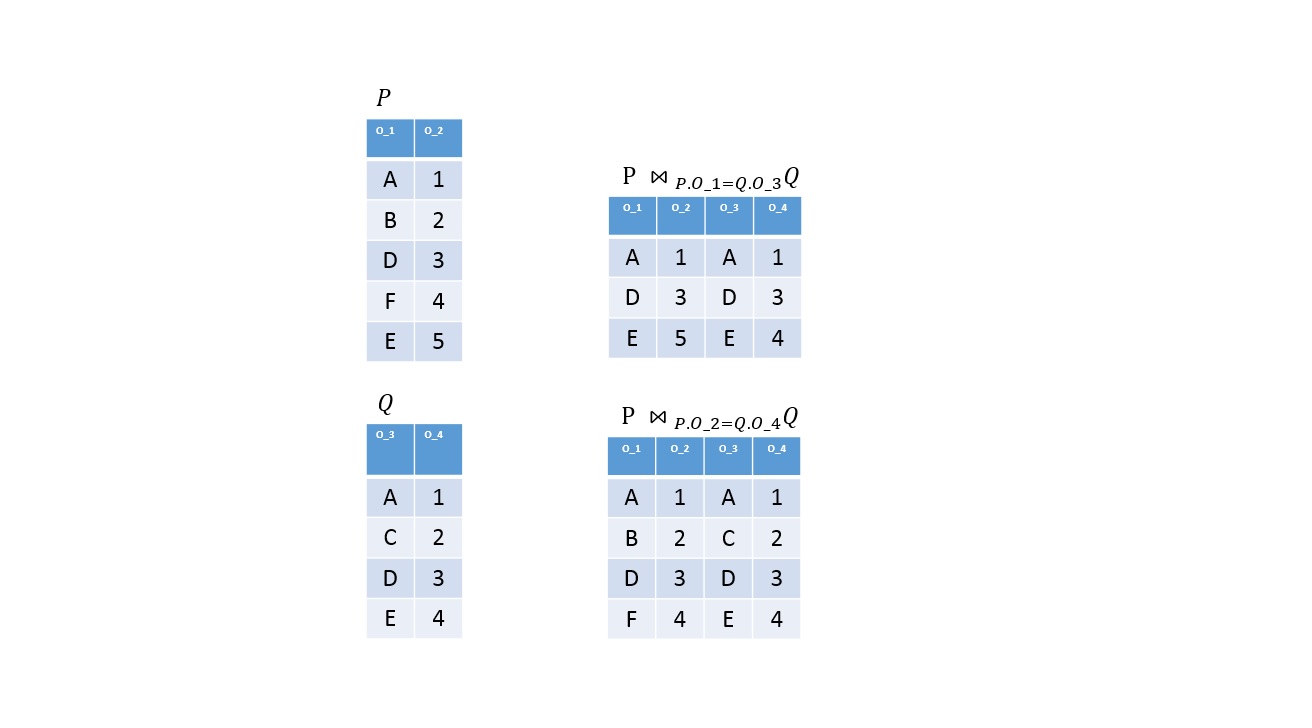
Egyenlő kapcsolás

Definíció

Legyen és két tetszőleges paraméter-reláció séma, és az és relációsémák feletti paraméter-relációk. Az egyenlő kapcsolás egy olyan kétoperandusú relációs algebrai művelet, mely a theta kapcsolás speciális esete abban az értelemben, hogy az feltételben a helyén kizárólag egyenlőség állhat. Jelölése a következő: . Az egyenlő kapcsolás származtatott művelet: .

Legyen és paraméter-reláció sémák, és az és feletti paraméter-relációk. Képezzük a két reláció egyenlő kapcsolását egy eredmény-relációba egy megadott () () feltételek mellett: .

Egyenlő kapcsolás

Külső kapcsolás

A korábbi alfejezetekben már megismertük, hogy a belső kapcsolás során az egyező rekordokal visszatérünk, a többi kimarad. Ezzel ellentétben a külső kapcsolásnál nemcsak azon rekordokat vesszük be az eredmény-relációba, hanem azokat is, melyek nem teljesítik a megadott feltételt. A külső kapcsolás kétoperandusú művelet. Az eredmény-reláció magába foglalja a bal, illetvbe a jobb oldali paraméter-relációkat is (az operandusok), amelyek nem felelnek meg a megadott feltételeknek. Vegyük figyelembe azt a tényt, amennyiben két paraméter-relációra (belső) kapcsolást hattatunk, az adatok egy része "el fog veszni". Egyes esetekben ezek az elvesztett adatok hasznos információkat tartalmazhatnak. A külső kapcsolás megőrzi azokat az információkat, amelyek egyébként elvesztek volna a (belső) kapcsolás alkalmazásával, a hiányzó adatokat NULL értékekkel helyettesítve. Attól függően, hogy mely adatokat kívánjuk megőrizni, három formáját ismerjük a külső kapcsolásnak:

  • Bal oldali külső kapcsolás - az eredmény-relációban a bal oldali paraméter-reláció azon sorai is szerepelnek, amelyek a jobb oldali paraméter-reláció egyetlen sorával sem párosítható. Ezen rekordokban a jobb oldali paraméter-relációból származó attribútumok értéke NULL.

  • Jobb oldali külső kapcsolás - az eredmény-relációban a jobb oldali paraméter-reláció azon sorai is szerepelnek, amelyek a bal oldali paraméter-reláció egyetlen sorával sem párosítható. Ezen rekordokban a bal oldali paraméter-relációból származó attribútumok értéke NULL.

  • Teljes külső kapcsolás - az eredmény-reláció mind a két paraméter-reláció párosítatlan sorait tartalmazza.

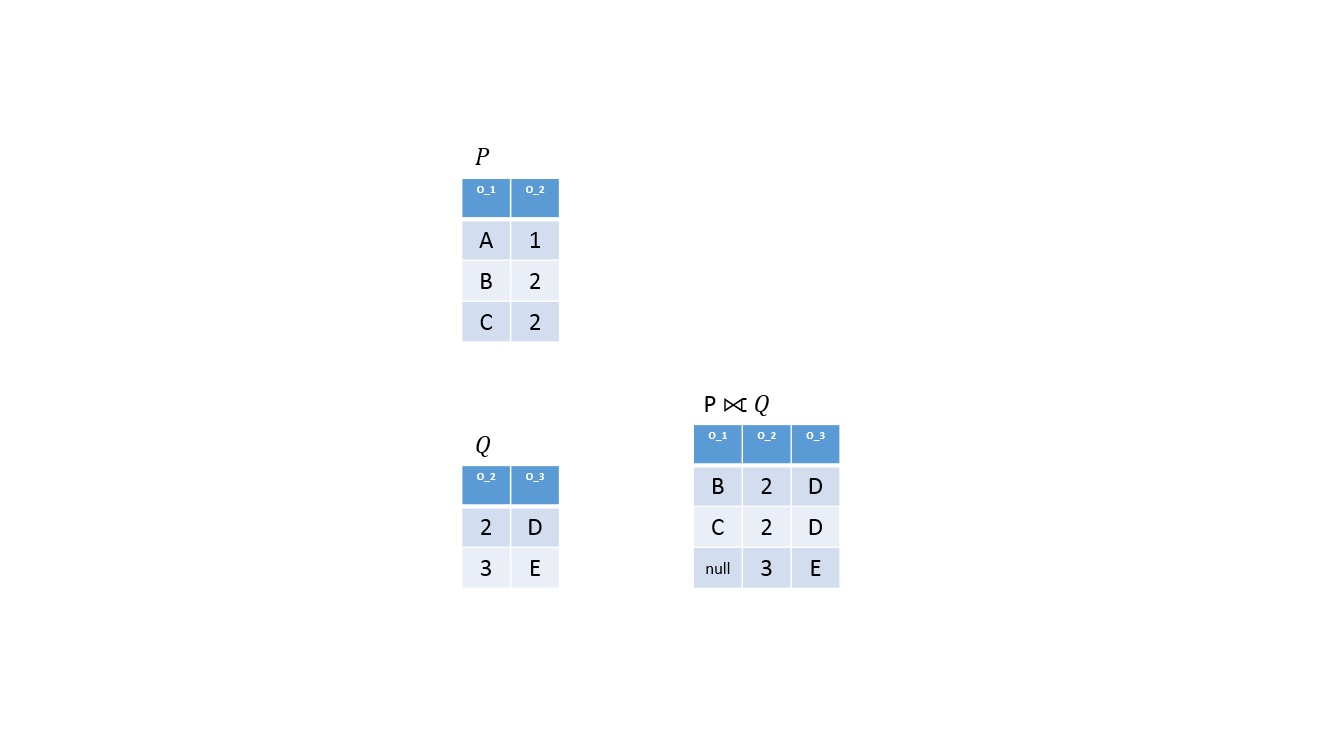
Jobb oldali külső kapcsolás

Definíció

Legyen és két tetszőleges paraméter-reláció séma, és az és relációsémák feletti paraméter-relációk. A jobb oldali külső kapcsolás egy olyan kétoperandusú halmazalgebrai művelet, melynél az eredmény-reláció séma megegyezik a természetes kapcsolásuk sémájával. Jelölése a következő: ⟖ . A jobb oldali külső kapcsolás nem kommutatív. A jobb oldali külső kapcsolás származtatott művelet: ⟖ = .

Az eredmény reláció az alábbi sorokat tartalmazza: paraméter-relációk természetes kapcsolásukból adódó sorok; a jobb oldali paraméter-reláció minden olyan sora, melyeknek a természetes kapcsolásnál a bal oldali paraméter-relációban nincs párja. Az eredmény-reláció jobb oldali paraméter-relációból az adott sor megfelelő mezőértékei, a bal oldali paraméter-reláció attribútumaihoz pedig NULL értékek kerülnek [35. oldal 16].

Legyen és paraméter-reláció sémák, és az és feletti paraméter-relációk. Képezzük a két reláció jobb oldali külső kapcsolását egy eredmény-relációba: ⟖ .

Jobb oldali külső kapcsolás

Bal oldali külső kapcsolás

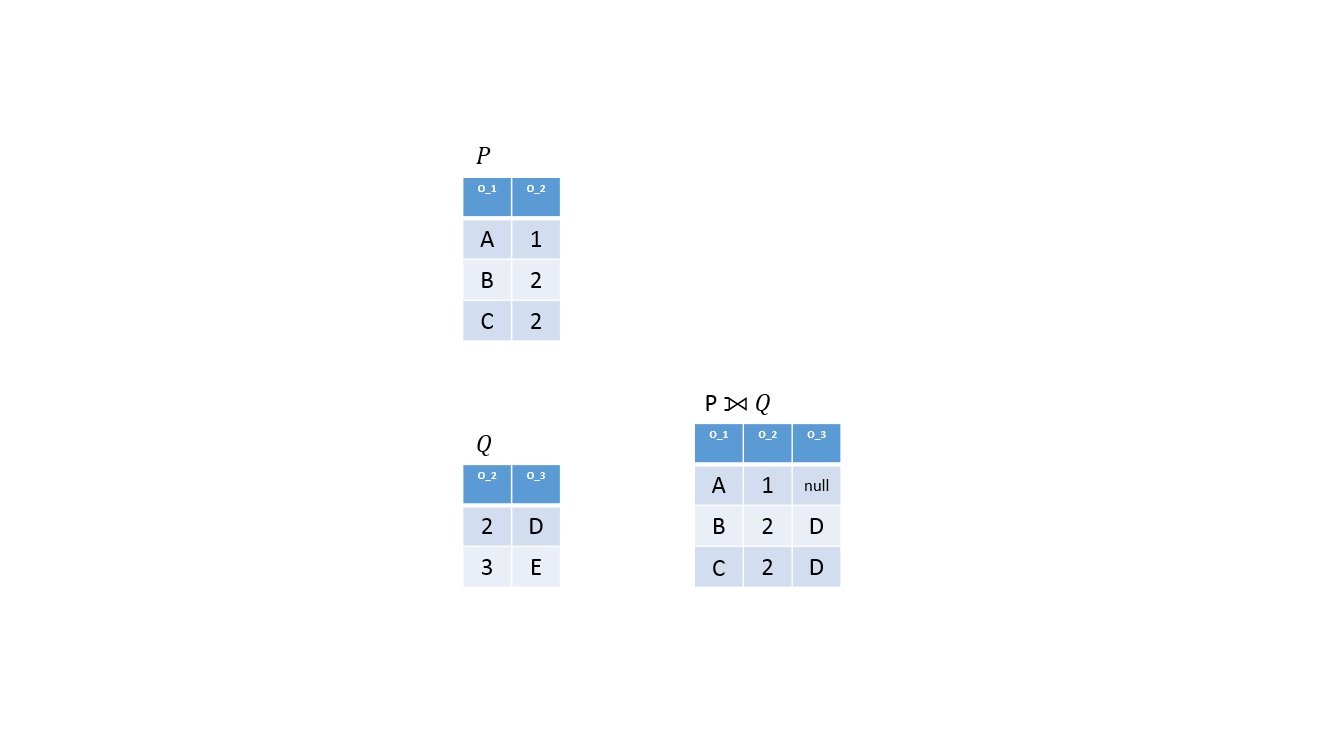
Definíció

Legyen és két tetszőleges paraméter-reláció séma, és az és relációsémák feletti paraméter-relációk. A bal oldali külső kapcsolás egy olyan kétoperandusú halmazalgebrai művelet, melynél az eredmény-reláció séma megegyezik a természetes kapcsolásuk sémájával. Jelölése a következő: ⟕ . A bal oldali külső kapcsolás nem kommutatív. A bal oldali külső kapcsolás származtatott művelet: ⟕ = .

Az eredmény reláció az alábbi sorokat tartalmazza: paraméter-relációk természetes kapcsolásukból adódó sorok; a bal oldali paraméter-reláció minden olyan sora, melyeknek a természetes kapcsolásnál a jobb oldali paraméter-relációban nincs párja. Az eredmény-reláció bal oldali paraméter-relációból az adott sor megfelelő mezőértékei, a jobb oldali paraméter-reláció attribútumaihoz pedig NULL értékek kerülnek [34. oldal 16].

Legyen és paraméter-reláció sémák, és az és feletti paraméter-relációk. Képezzük a két reláció bal oldali külső kapcsolását egy eredmény-relációba: ⟕ .

Bal oldali külső kapcsolás

Teljes külső kapcsolás

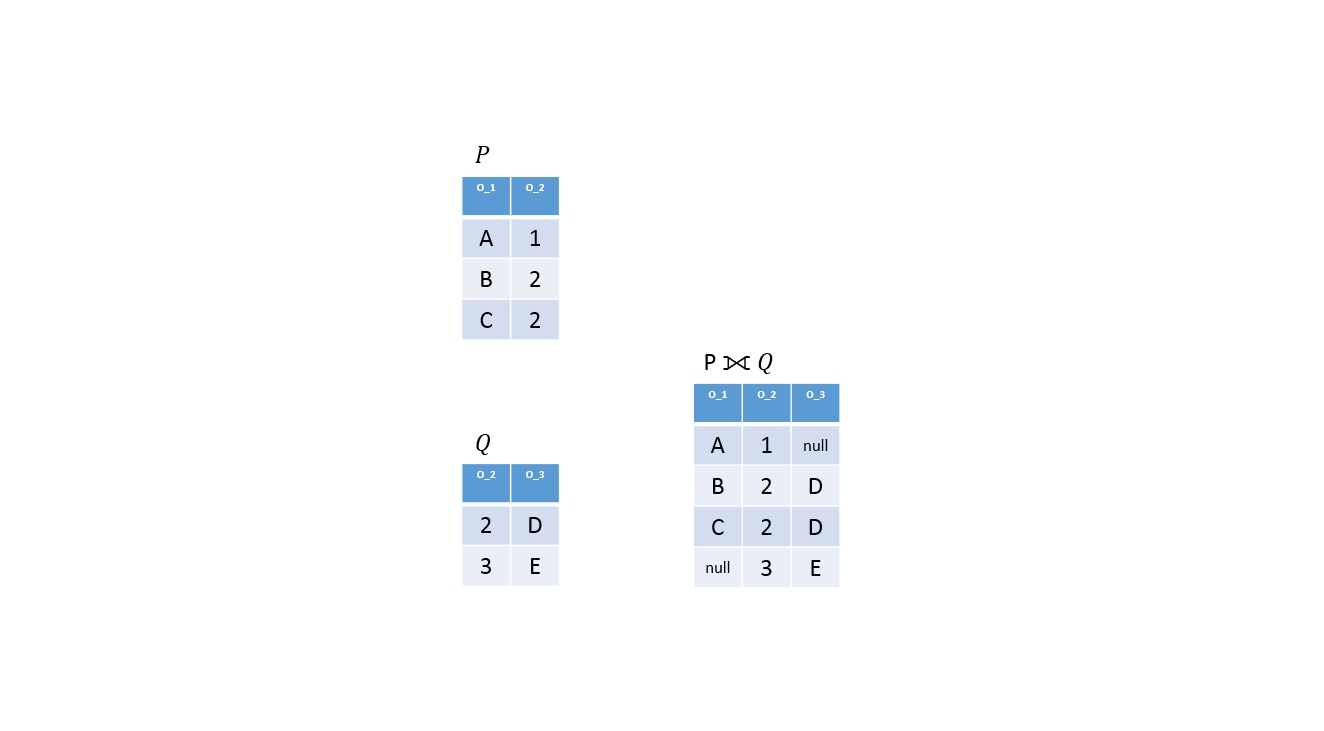
Definíció

Legyen és két tetszőleges paraméter-reláció séma, és az és relációsémák feletti paraméter-relációk. A teljes külső kapcsolás egy olyan kétoperandusú halmazalgebrai művelet, melynél az eredmény-reláció séma megegyezik a természetes kapcsolásuk sémájával. Jelölése a következő: ⟗ . A teljes külső kapcsolás nem kommutatív. A teljes külső kapcsolás származtatott művelet: ⟗ = ( ⟕ ) ( ⟖ ).

Az eredmény reláció az alábbi sorokat tartalmazza: paraméter-relációk természetes kapcsolásukból adódó sorok; minden olyan sor, melyek a paraméter-relációk természetes kapcsolással nem párosított sorai. Az eredmény-reláció bal oldali paraméter-relációból az adott sorattribútumaihoz a megfelelő mezőértékek, a másik paraméter-reláció attribútumihoz pedig NULL értékek kerülnek [34. oldal 16].

Legyen és paraméter-reláció sémák, és az és feletti paraméter-relációk. Képezzük a két reláció teljes külső kapcsolását egy eredmény-relációba: ⟗ .

Teljes külső kapcsolás

Irodalomjegyzék

[1]
 Vue.js core team. Vue.js: The Progressive JavaScript Framework. https://vuejs.org, Legutóbb megtekintve: 2019. április 22.
[2]
 Vue.js core team. API, Global Config, directive. https://vuex.vuejs.org/vuex.png, Legutóbb megtekintve: 2019. április 22.
[3]
 Vue.js core team. API, Global Config, computed. https://vuejs.org/v2/api/#computed, Legutóbb megtekintve: 2019. április 22.
[4]
 Vue.js core team. API, Global Config, components. https://vuejs.org/v2/api/#components, Legutóbb megtekintve: 2019. április 22.
[5]
 Vue.js core team. Vue-CLI. https://cli.vuejs.org/guide/creating-a-project.html#vue-create, Legutóbb megtekintve: 2019. április 22.
[6]
 Vue.js core team. Vue-router. https://router.vuejs.org/guide/#html, Legutóbb megtekintve: 2019. április 22.
[7]
 Vue.js core team. Render Functions and JSX. https://vuejs.org/v2/guide/render-function.html, Legutóbb megtekintve: 2019. április 22.
[8]
 w3schools core team. JavaScript RegExp Reference. https://www.w3schools.com/jsref/jsref_obj_regexp.asp, Legutóbb megtekintve: 2019. április 22.
[9]
 Google Chrome DevTools core team. Chrome DevTools. https://developers.google.com/web/tools/chrome-devtools, Legutóbb megtekintve: 2019. április 22.
[10]
 Node.js core team. Node.js® is a JavaScript runtime built on Chrome's V8 JavaScript engine. https://nodejs.org/en/, Legutóbb megtekintve: 2019. április 22.
[11]
 NPMJS core team. NPMJS. https://www.npmjs.com, Legutóbb megtekintve: 2019. április 22.
[12]
 ExpressJS core team. Express Fast, unopinionated, minimalist web framework for Node.js. https://expressjs.com, Legutóbb megtekintve: 2019. április 22.
[13]
 EJS core team. EJS: Embedded JavaScript templating. https://ejs.co, Legutóbb megtekintve: 2019. április 22.
[14]
 Olga Filipova. Learning Vue.js 2. Packt Publishing Ltd., Livery Place, 35 Livery Street, Birmingham, B3 2PB, UK, 3, 2016.
[15]
 E.F. Codd. A relational Model of Data for Large Shared Data Banks. Communications of the ACM, 13 (6) 1970.
[16]
 Papp Edit. Adatbáziskezelés. Booklands 2000 Könyvkiadó Kft., 5600 Békéscsaba, Dr. Becsey Oszkár u. 42., 1, 2004.
[17]
 Nemzeti Szakképzési és Felnőttképzési hivatal. Szoftverfejlesztő tanfolyam. https://www.nive.hu, Legutóbb megtekintve: 2019. április 22.
[18]
 JavaScript.info core team. JavaScript.info. https://javascript.info/promise-basics, Legutóbb megtekintve: 2019. április 22.
[19]
 Craig Buckler. Sitepoint (JavaScript) - Understanding ES6 Modules. https://www.sitepoint.com/understanding-es6-modules/, Legutóbb megtekintve: 2019. április 22.

← 3. MySQL→