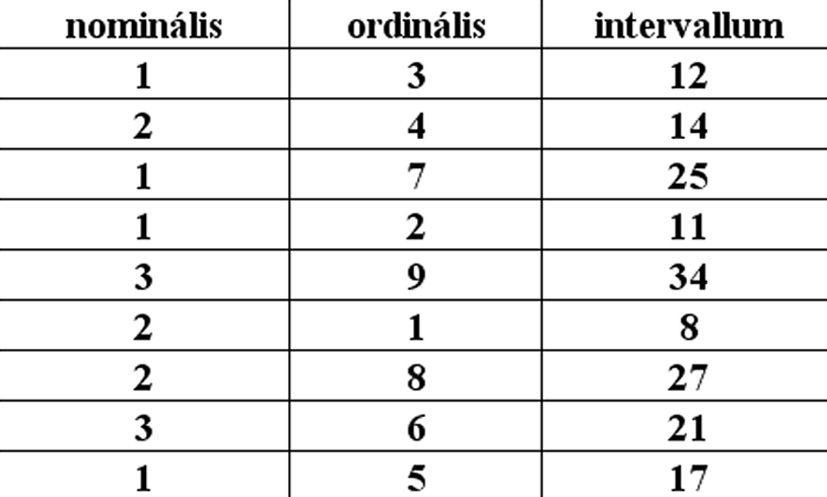
A mintavételezést úgy kell megtervezni, hogy a valóságnak megfelelő állapotokat ábrázolja, valamint a jelenlévő változásokat is reprezentálja. Ez gyakorlati szempontból a megfelelő tér- és időbeli felbontást jelenti, vagyis a minták minden jellemző helyet érintsenek, és a változás minden lehetséges idejét tartalmazzák. Hiba lenne a 30 m-es geometriai felbontású műholdképpel 5-10 méteres változásokat keresnünk, mint ahogy hiba az is ha egy 4 óránként mért meteorológiai paraméter alapján 30 perces változásokat regisztrálunk. Ellenben felesleges 5 méteres felbontású műholdképet beszerezni, ha tudjuk, hogy csak 1:100.000-es térképre van szükségünk (lásd. 4-4. ábra). A jelenségek megfelelő ábrázolásához szükséges méretarányt elsősorban a mintavétel száma, eloszlása, sűrűsége határozza meg. A később elemzendő mintákat gyűjthetjük véletlenszerűen, módszeresen, vagy súlyozottan. Az első esetben a mintákat minden helyen vagy időben azonos valószínűséggel vesszük, míg a második esetben egy adott szabálynak megfelelően választunk; pl. 100 m-ként felvételezünk (lásd. 4.7. ábra). Ha egy terület déli részén sokkal tagoltabb a domborzat, mint máshol, akkor ennek a megfelelő bemutatásához ott sokkal sűrűbb mintavétel szükséges, vagyis súlyozottan gondolkodunk. A valóság különböző részhalmazokat tartalmaz és a mintákat úgy kell venni, hogy megfelelően jellemezzék azokat. Fel kell ismernünk a felvett numerikus értékek skáláját, mivel ez meghatározza az adatokkal kapcsolatos matematikai műveleteket (4-16. ábra): - a nominális skálán a számok csupán az azonosítás megállapítására valók. Területhasználati térképen: 1: beépített terület, 2: mezőgazdasági terület, 3: természetközeli terület, 4: vizes terület. - Az ordinális skála, sorrendi skála. Ha a jelenségek 1, 2, 3… értékeket kapnak, akkor annak jelentősége van. Azért lehetett az egyik mintaterület (vagy pont) 1-es kód értékű, mert vagy nagyobb, vagy jelentősebb, vagy valamiért előrébb való, mint a 2-es terület. Ilyen lehet egy közúthálózat térkép, ahol a kódértékek szerint: 1: autópálya, 2: autóút, 3: I. rendű főút, 4: II. rendű főút. A sorrendiségből azonban nem derül ki, hogy mennyivel jelentősebb az 1-es kód, mint a többi. - Az intervallum skálán a számok közötti eltérés (intervallum) a lényeges. A különbséget tudjuk számolni az egyes értékek között. Meg tudjuk mondani, hogy két meteorológiai állomás között mekkora hőmérsékleti különbség van. - Az arányskálán – az intervallum skálával ellentétben – a mérésnek már van egy abszolút „0” értéke, aminek köszönhetően nem csak a különbségnek, hanem az osztásnak is van értelme. Amikor egy 2000 m magas hegyet vizsgálunk, akkor elmondhatjuk, hogy ez kétszer olyan magas, mint egy 1000 m-es csúcs, mert a 0 m tengerszint feletti magasságból nézzük és nem egy 500 m magasságú völgypontból. Ezt felismerve a területhasználati térképen 3-as kódértékből (erdőterület) nem vonjuk ki értelmetlenül az 1-es kódot (beépített terület), viszont ha kíváncsiak vagyunk a hidrogeográfiai viszonyokra, akkor érdemes kivonnunk a Tisza tavaszi vízállásából a nyári értéket.