Az egyik fő feladatunk tehát a jelenségek, illetve térbeliségük, időbeli változásuk ábrázolása. Két különböző modell terjedt el erre a célra, a raszter-, és a vektor alapú rendszerek, illetve ide vehetjük kettejük keverékét is, az un. hibrid rendszereket. Raszter, vagy cella alapú információs rendszerek, és a vektoros alapú rendszerek különbözőképpen vizsgálják a térbeli jelenségeket. A raszteres rendszerek a térben található jelenségeket, míg a vektoros rendszerek a jelenségek térbeli elhelyezkedését vizsgálják. Míg a vektoros modellben a "hol van?", addig a raszteres modellben a "mi van ott?" kérdésekre kaphatunk könnyebben választ. A vektoros rendszerek az objektumokat, és azok jellemzőit tárolja. Ezen jellemzők között találhatjuk az adott jelenség térbeli elhelyezkedését mutató adatokat (x,y koordináta, kiterjedés, z koordináta, stb.). A raszter alapú rendszerek ezzel szemben a teret osztják fel szabályos, különálló részterületekre. Ezeket a részterületeket celláknak hívjuk. Minden cella a vizsgált terület egy jól definiált részlete. A modellben a cellák területén található jelenségek vizsgált jellegzetességét tároljuk.
A digitális képfeldolgozás során használt képek alatt olyan digitális állományokat értünk, melyek valamilyen képkezelő, képfeldolgozó szoftver segítségével bemutatnak egy tárgyat, vagy a földfelszín egy részét. A digitális képek adatállományokban, más néven képfile-okban találhatók, s valamilyen adathordozón, mágnesszalagon, CD-n, mágneslemezen, stb. tárolják őket.
A háló alapú képfeldolgozó rendszerekben a kép legkisebb önálló eleme a pixel, vagy raszter, melynek helye és értéke van. A helyet az oszlop és sor koordináták, descartesi x, y koordináták, vagy földrajzi koordináták is meghatározhatják, míg a pixel értéke egy szám, mely valamilyen módon reprezentálja az adott terület egy tulajdonságát, vagy a mérés eredményét (pl. reflektancia, tengerszint feletti magasság, stb.). A különböző tulajdonságok mérési eredményeit önálló sávokban tároljuk, így pl. a különböző spektrális tartományokban mért reflektancia értékek általában egy képfileban, de más-más sávban találhatók.
A képfeldolgozó rendszerekben gyakran párhuzamosan használják a sáv és a réteg fogalmát. Mindkét fogalom használható azzal a megjegyzéssel, hogy a digitális kép egy sávja és egy űrfelvétel egy adott spektrális tartományra (sávra) vonatkozó adatai közötti kapcsolatot pontosan meg kell határozni , másrészt ha a digitális, többsávú képek sávjait egy térinformatikai rendszerben (GIS) használjuk fel, akkor ott már csak rétegekről beszélhetünk. A képfeldolgozás során új képek készülnek, melyek lehetnek raszter vagy vektor alapúak, ezért érdemes az eredeti kép sávjaitól megkülönböztetve ezeket már csak rétegeknek nevezni, pl. annotációs réteg.
A numerikus adatok feldolgozása során nem közömbös, hogy a pixelértékek milyen típusúak, valamint milyen formátumban tároljuk azokat. A pixelértékek egy raszterfileban lehetnek nominális, rend, intervallum és arány típusúak. Az első két típust tartalmazó rétegeket tematikus állományoknak nevezik. Az intervallum vagy arány típusú változókkal többnyire folyamatosan változó jelenségeket írunk le, pl. domborzat magassága, hőmérséklet, stb., ezért az ilyen adattípusokat tartalmazó rétegeket folyamatos rétegeknek nevezzük.
A cellák alaprajza sokféle lehet, négyzet, téglalap, hatszög, háromszög, stb. A gyakorlatban az egyszerű kezelhetősége miatt a négyzet alakú cellákat használják, a továbbiakban mi is ezt fogjuk tenni.
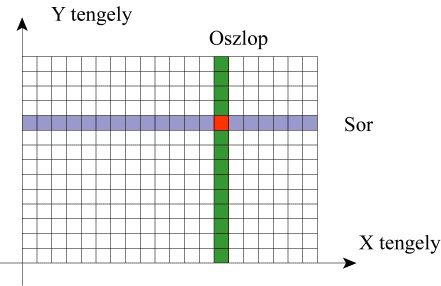
Az egybevágó cellákat oszlopokból és sorokból álló mátrixba rendezzük, úgy hogy azok területünket hézag nélkül lefedjék. Ez a mátrix gyakorlatilag egy szabályos rácsháló, amelyet a vizsgált területre helyezünk. Minden cellát a sor és oszlopsorszáma azonosít.
A modellünket két fő részre oszthatjuk: a cellák értékeinek halmaza, és a hozzájuk tartozó kísérő információk, úgy mint sor, oszlopszám, felbontás, cellaméret, földrajzi elhelyezés. Bizonyos esetekben még egy harmadik fő csoportot is találhatunk, a leíró, vagy attribútum adatok összességét.
A felbontás a cellamérettől, illetve a sor és oszlopszámtól függ. A cellaméretet a feldolgozás céljának megfelelően kell megválasztani, de természetesen a forrás adatok információsűrűsége (pl. térkép méretaránya) is jelentősen befolyásolja azt. Figyelembe kell vennünk, hogy a cellák alakja (négyzet) csak nagyon speciális esetekben követi az ábrázolni kívánt jelenségek alakját illetve határait. Túl nagy cellaméretet választva a jelenségek körvonalai torzulnak, jelenségek veszhetnek el. Kis cellaméret esetén a jelenségeket pontosabban ábrázolhatjuk, nincs szükségünk nagy fokú generalizálásra, viszont a tároláshoz szükséges hely és a feldolgozás ideje jelentősen megnövekedhet a tárolt információ nagyfokú redundanciája miatt. Gondoljunk bele, hogyha a cellaméretet felére csökken, akkor ugyanazon terület ábrázolásához négyszeres mennyiségű cella szükséges, és ez (nem számítva az adattömörítési módszerek használatát, lásd később) négyszeres tárolókapacitás és szintén négyszeres feldolgozási idő növekedést jelent.
۩ A geometriai felbontás hatása a raszteres adatok megjelenítésére
۩ Méretarány változtatása a raszteres adatok megjelenítésére - video 1:14p
Ahhoz, hogy tudjuk, melyik cellánk a valóság melyik részletét ábrázolja, minden cellánk földrajzi koordinátáit ismernünk kell. Mivel a cellák szabályosak, elegendő tárolnunk a modellben egy fix pont, ami a cartesian koordinátarendszerünk kezdőpontja (pl. a raszterháló bal alsó, vagy bal felső sarka), földrajzi koordinátáit. Ismernünk kell továbbá a cellák méreteit a megadott mértékegységben (pl. egy cella 30x30 méter, vagy 1° x 1° kiterjedésű). Ezen ismeretek birtokában már ki tudjuk számítani bármely sor és bármely oszlop koordinátáit. A földrajzi koordináták ismeretében tudjuk a raszterben tárolt jelenségeinket más ugyanarra a területre vonatkozó jelenségekkel összehasonlítani, és közöttük műveleteket végezni.
A cellaérték jelöli, hogy az adott cella által lefedett területen milyen jelenség a jellemző. Ez a jellemző egy szám, ami a jelenségre utal. Ez lehet egy a jelenséghez rendelt kód, de lehet tényleges mérési érték is (pl. tengerszint feletti magasság). A cellaértékek jelentése a már tárgyalt négy típust képviselheti, az arány, a intervallum, rang, és osztály típust.
Feloszthatjuk az értéktípusokat a tárolási módjuk alapján is. Ez tulajdonképpen a számítástechnika világából már ismert változótípusokat jelenti. Tárolhatjuk az egész értékeinket egyenként 8,16,32,64 biten előjellel, illetve előjel nélküli pozitív számokként. A nem egész számok tárolása általában 32 vagy 64 biten történik. Tudnunk kell, hogy az éppen felhasznált típus milyen korlátokkal rendelkezik, úgy mint értékhatárok (min, max) vagy a nem egész számok pontossága. Mindig az adott feladat dönti el, hogy milyen lehetséges értékek fordulhatnak elő, illetve milyen pontosságot akarunk elérni. Célszerű a lehető legkisebb tárigényű de a feladatnak még megfelelő típust használni, hiszen így a tároláshoz kevesebb helyre van szükségünk, és a feldolgozás is gyorsabb lehet. A kiválasztásnál további fontos szempont az értékek jelentésének figyelembevétele. Pl. osztály (nominális) típusú értékek kódolásához egész számokat használunk.
Sokszor előfordul, hogy a vizsgált terület nem téglalap alakú és a terület valamint a köré írható legkisebb téglalap közötti részeket nem akarjuk modellünkben ábrázolni, vagy a jelenségeink nem fedik le a vizsgált területet, és a köztük található tér nem tartalmaz a modellünk számára fontos információkat, esetleg a terület egyes részeiről nem áll rendelkezésünkre információ. Ekkor azok a cellák, amelyek ezekre területekre esnek, egy speciális értéket kapnak, amely az értékelhető információ hiányát jelöli. Ezt az értéket úgy kell megválasztani, hogy ez jelenségeink értékkészletétől eltérő szám legyen. Egyes rendszerek a FIR műveletek során az ilyen un. nodata mezőket automatikusan kezelik. Pl. az ARC/Info rendszerben ez az érték mindig -9999, a TNT rendszerben ez az érték változhat, lehet pl. nulla, -32768, stb. az adattípustól és az adat jelentésétől függően. Mindkét módszernek megvan a saját előnye, az előbbi esetben ez a nodata kezelésének egységessége, míg a másodikban a feladathoz igazodó rugalmasság.
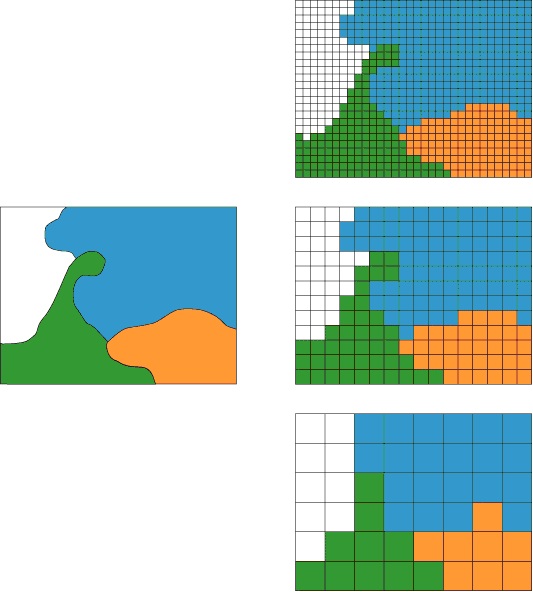
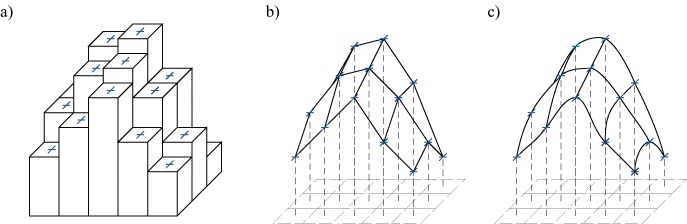
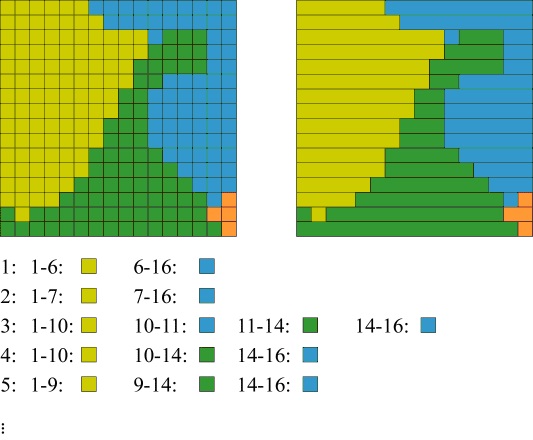
A cellák értékeinek megállapításánál (raszterizálás) egy szabályos rácshálót helyezünk a vizsgált területre. Minden cellához hozzárendelünk egy értéket (cella érték), amely jellemzi az adott cellát. Egy cellán belül több különböző jelenség is előfordulhat, ilyenkor a cellaérték megállapítása különböző módszerekkel történhet. A cellaérték jelentheti a cella középpontjában található jelenséget, a cella legnagyobb részét betöltő jelenséget, vagy egy speciális jelenséget, ami megtalálható a cellán belül. Így ugyanannak a cellának különböző értékeket is adhatunk a használt módszer függvényében. Arra a kérdésre, hogy melyik érték-megállapítási módszer adja a legjobb eredményt, az adott feladat és a forrás adatok ismeretében kaphatunk választ. Nézzük tehát a három legfontosabb cellaérték-megállapítási módszert, amelyek: középponti jelenség választása (centroid), uralkodó jelenség választása (predominant) és a legfontosabb jelenség választása (most important).
A cellaérték meghatározása a cellát kitöltő jelenségek cellán belüli kiterjedésének nagysága alapján történik. Ez területi jelenségeket vizsgálva az egyes jelenségek cellából elfoglalt területének vizsgálatát jelenti. Pl. területhasznosítást vizsgálva az adott cellának 25%-a szántó, 10%-a közút, 65%-a gyümölcsös, akkor a cella a gyümölcsösnek megfelelő kódot fogja kapni értékül. Ez a módszer legjobban a tematikus, nem folytonos (diszkrét) jelenségek ábrázolásakor használható jól, ahol a jelenségek határai jól elkülöníthetőek. Ilyenek, pl. a már említett területhasznosítási térképek, talajtérképek, de ide tartoznak a vonalas objektumokból, vagy pontokból álló jelenségek is, pl. folyóhálózat, közúthálózat, stb.
Ennél a módszernél a cella a cella középpontjában található jelenségnek megfelelő értéket kapja. Ez a módszer legjobban a folyamatos jelenségek modellezésénél alkalmazható, mint pl. magassági értékek, légszennyezés, stb.
A cella területén előforduló jelenségek közül a modellünk számára legfontosabb jelenséget választjuk ki. A rangsorolás a vizsgálatunk céljától és a forrás adatoktól függ, pl. ha a előfordulnak kis területű de a vizsgálat szempontjából fontos területek, az előző két módszernél ezek esetleg nem kerülnének bele a modellbe ( nem esik a cella középpontjába, és nem is foglalja el egy cella legnagyobb részét sem). A módszer szintén jól használható vonalas, és pontszerű jelenségek esetén is.

ábra Ugyazon jelenségeket ábrázoló raszteres modell különböző cellaértékekkel, a különböző cellaérték megállapítási módszerektől függően
A jelenségek kombinációjának választása
A cella területén található jelenségek valamilyen aggregátumának készítését jelenti. Legáltalánosabban a távérzékelésben használják, ahola cellaértékek a cella területén található jelenségek reflektanciájának átlagos értékét jelentik. Az átlagképzésen kívül azonban használhatunk más matematikai módszereket is a cellaérték megállapításához, pl. minimum, maximum, szórás, súlyozott átlag, stb.
Leíró (attribútum) adatok
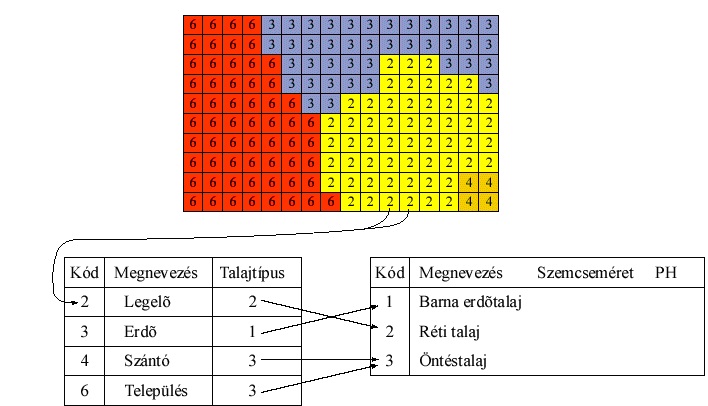
Sokszor előfordul, hogy egy-egy diszkrét jelenség nem csak egy jellemzőjét vizsgáljuk a feldolgozás során. Pl. egy talajtérkép foltjainak PH-értékét és átlagos szemcseméretét egyaránt ismernünk kell. Egyes FIR-ekben (főleg a korábbi időkben) ilyen esetben minden vizsgált tulajdonság rögzítéséhez külön raszterhálóra volt szükség.
Egy másik lehetőség, hogy a jelenségek jellemzőit egy relációs adatbázisban tároljuk, és a jelenségek foltjainak azonosítóit használjuk a cellaértékek és a leíró adatok közötti reláció létrehozására. Természetesen a leíró adatok további relációkat is tartalmazhatnak.
Földrajzi jelenségek és ábrázolásuk raszteres modellben
Diszkrét jelenségek (Discrete features) és ábrázolásuk
Az egyes jelenségek elhelyezkedése jól definiált, de ezt közvetlenül nem rögzítjük, csak a cellaértékeket vizsgálva tudunk következtetni a forrás-jelenségre. Így a modell alapján az eredeti jelenségek alakja nehezen, és kérdéses pontossággal (függ a jelenség alakjától, környezetétől, valamint a felbontástól) állítható vissza. A határvonal erősen lépcsős, csak generalizálással, vagy speciális illesztőalgoritmusokkal simítható el. Hasonlóképpen a vektoros rendszereknél ismert topológiát sem használhatjuk, a szomszédságot csak a cellaértékek alapján tudjuk megállapítani, pl. két jelenségnek közös határa van, ha két jelenségre utaló érték két egymás melletti cellában található meg. Egy cellának nyolc szomszédja van, amelyek helyét a hálóban egyszerűen megkaphatjuk, pl. a balfelső szomszéd helyzetét a sor és oszlopszámból egyet kivonva kapjuk.
Pontszerű jelenségek
A pont jelenségek a raszteres adatmodellben egy cellával ábrázolhatóak, amely a legkisebb területi egység. Mivel a celláknak van területük, az ábrázolás pontossága a cella átlójának felének adódik. További problémát jelenthet, ha egy cella területére egynél több pontszerű jelenség esik. A pontszerű jelenségek nem fedik le a vizsgált területet, így a modellünkben szükséges nodata érték használata.
Vonalas jelenségek
A jelenséget kapcsolódó cellák sorozatával írhatjuk le. Nem elégséges felbontás esetén a különböző vonalak nem különíthetőek el egymástól. A teljes vizsgált területet, hasonlóan a pontszerű jelenségekhez, itt sem fedik le a jelenségek.
Területi vagy poligon jelenségek
A jelenségeink az adott felbontás mellett több irányú kiterjedéssel rendelkeznek, ábrázolásuk egymással kapcsolódó cellákkal történik, ahol a cellahalmaz körvonalai a poligonunk körvonalait közelítik. Ezek a körvonalak azonban lépcsősek, és előfordulhat, hogy a valóságban egymással nem érintkező területek a modellben egymás mellé kerülnek. Ezeken a problémákon a felbontás javításával javíthatunk. Itt már a poligonok lefedhetik az egész vizsgált területet, de bizonyos esetekben a jelenségek között találunk nodata értékkel jelölt területeket.
3.6. ábra - Különböző típusú nem folytonos jelenségek ábrázolás raszteres modellben (pont, vonal, terület)

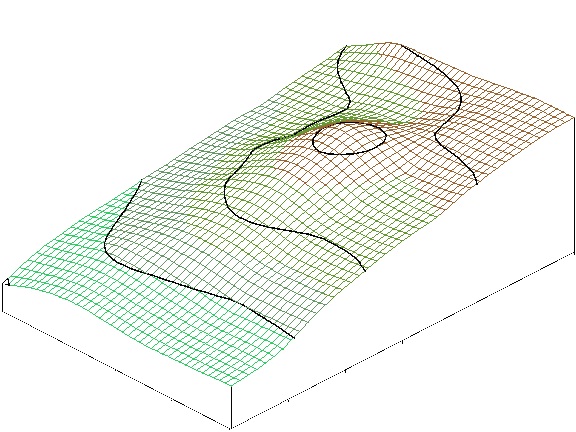
Folytonos jelenségek (Continuous features) és ábrázolásuk A folytonos jelenségek modellezésénél az un. középponti jelenség választása elv alapján adunk értékeket a raszterháló celláinak, azaz minden cella értéke a jelenségnek a cella középpontjában mért értékét mutatja.
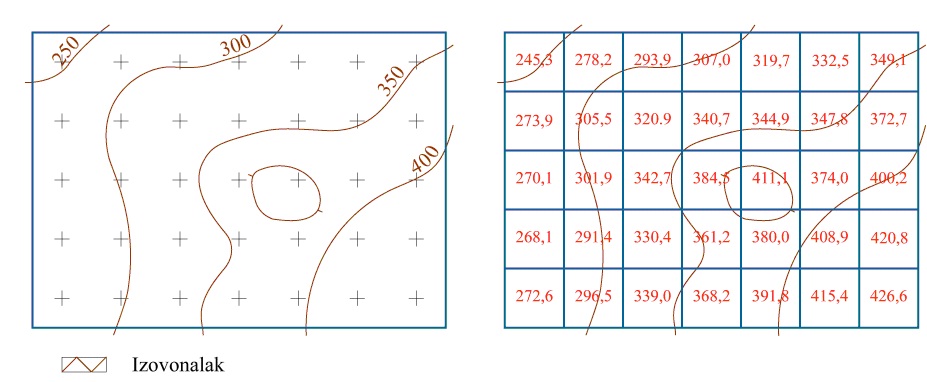
Mivel folytonos jelenségeknél a modellünkben az egyes cellaértékek a cellák középpontjának értékét képviselik, így szükségünk van különböző interpolálási módszerekre, ahhoz hogy a modellezett terület bármely pontjára (ami nem cellaközéppont) tudjunk értéket adni. Ha ismert a jelenség értékeinek eloszlástípusa, akkor a köztes érték kiszámításához felhasználhatjuk jellemző eloszlásfüggvényt. Nehézséget jelent, hogy a jelenségek a természetben általában nem mutatnak szabályos eloszlást, így a köztes értékek mindig csak közelítők. Az interpolálási módszereknek alapvető követelménye a gyors kiértékelhetőség, hiszen esetenként rengeteg magassági értéket kell számítani. A leggyakrabban használt interpolálási módszerek a keresett magassági értékű pont környezetében található ismert z értékek alapján határoz meg z értéket. A felszín finomságát javíthatjuk azzal, hogy növeljük a keresett értékű pont vizsgált környezetét. Felhasználhatjuk a legközelebbi egy, négy, tizenhat, stb. cellaközéppont z értékeit, de a finomsággal együtt a feldolgozási idő is nő. A szomszédok száma szerint az interpolációs módszerek a következők:
Legközelebbi szomszéd interpoláció (nearest neighbor)
Ennél az interpolálási módszernél a pontunk z értékét a legközelebbi cellaközéppont értékének vesszük. Ez gyakorlatilag azt jelenti, hogy a cella értékét kiterjesztjük az egész cellára. A módszer pontossága legtöbbször nem kielégítő, lépcsős felszínt eredményez.
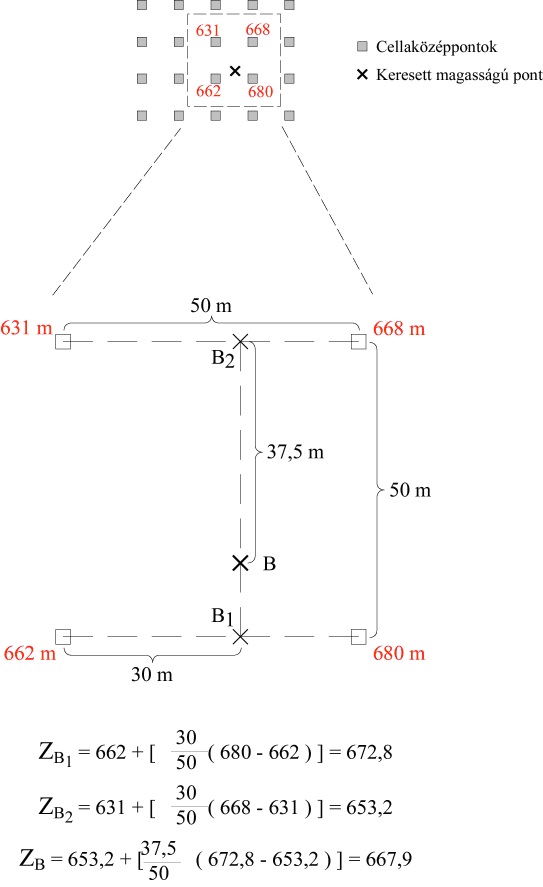
Bilineáris interpoláció (bilinear)
A keresett z értéket a pontunk legközelebbi négy szomszédjának értékéből számítjuk a súlyozott távolságok alapján. A módszer az ábrán követhető nyomon. Először kiszámítjuk a felső és az alsó köztes pont (Z1 és Z2) z értékét, majd ezekből hasonlóképpen a keresett értéket. Geometria megközelítésben a keresett z érték a pontunkon átmenő függőleges egyenes, és ponthoz legközelebb eső négy ismert z értékű pont (cellaközéppontok a térben) által meghatározott négyszög metszéspontjának z koordinátája.
Ezt az interpolációs eljárást kiterjeszthetjük a tizenhat legközelebbi szomszédra is, így még finomabb felszínt kapunk. (cubic convolution)
A raszteres adatmodell egyik sajátossága - diszkrét jelenségtípusok esetén - az adatok nagyfokú redundanciája, de a felbontást már nem csökkenthetjük Pl. egy modellben nagy foltokat is találunk azonos értékekkel, de a felbontás csökkentése a foltok határain, illetve a kisebb foltok esetében adatvesztéssel járna. Ilyen esetekben hasznosak az adattömörítési technikák. Bizonyos technikák bizonyos adattípusoknál jó eredménnyel használhatóak, míg másoknál használatuk nem jár helymegtakarítással. A megfelelő tömörítés kiválasztásánál azt is figyelembe kell venni, hogy későbbi feldolgozások során milyen műveleteket tudunk elvégezni az adatok kitömörítése nélkül, hiszen ha minden művelet előtt ki kell tömöríteni, illetve művelet után vissza kell állítani a tömörített adatstruktúrát, akkor a feldolgozási idő jelentősen megnövekedhet. Ezeknek a szempontoknak a figyelembevételével vizsgálunk meg néhány tárolási, tömörítési technika alapelvét.
Cella alapú tárolás (Cell by cell)
Ha minden cellánk különböző értékekkel rendelkezik, akkor a legcélszerűbb minden cellánk értékét külön-külön tárolni. Ez fordul elő folytonos jelenségek esetén. A tárolás történhet sor vagy oszlopfolytonosan, a gyakorlatban azonban legtöbbször a sorfolytonos megoldást alkalmazzák. Ez azt jelenti hogy a cellaértékek tárolása a bal felső cella értékével kezdődik, majd jobbra haladva a sor végéig tart, ezután folyamatosan következik a második sor első eleme, és így tovább sorra az összes elem. Az n. sor m. elemének pozíciója a sorozatban egyszerű szorzással és összeadással megkapható.
A jelenség alakját leíró kód a lánc-kód (chain code)
A vonalas jelenségek leírására szolgál a lánc-kód (chain code). Itt minden egyes jelenséget a kezdőpontjából induló cellaméret nagyságú egységvektor-sorozattal írunk le. Az egységvektorokat az égtájaknak megfelelően pl. a következőképpen kódolhatjuk: Észak=0, Kelet=1, Dél=2, Nyugat=3, de létezik nyolc irányú kódolás is. Alkalmazható a módszer területek ábrázolására is a kerület vonalának kódolásával. A fent leírt módszer nem terjedt el igazán, mivel alkalmazása nehézkes, a vektoros szemléletet próbálja raszteres modellbe átültetni.
Legnagyobb négyzetek tárolása (medial axis transformation)
E módszer szerint a jelenségeket a benne található legnagyobb négyzetekre osztjuk, és az így kapott négyzetek kezdőpontját és nagyságát tároljuk.
Sorkifejtő tárolás (Run-length code)
Ha a sorokban az egymás melletti cellák több esetben azonos értékekkel rendelkeznek, akkor használható ez a tömörítési módszer. Az azonos cellaértékeket csak egyszer tároljuk, megadva a sor számát, illetve azt, hogy hányadiktól hányadik oszlopig találhatjuk ezt az értéket. Elve az ábrán látható.
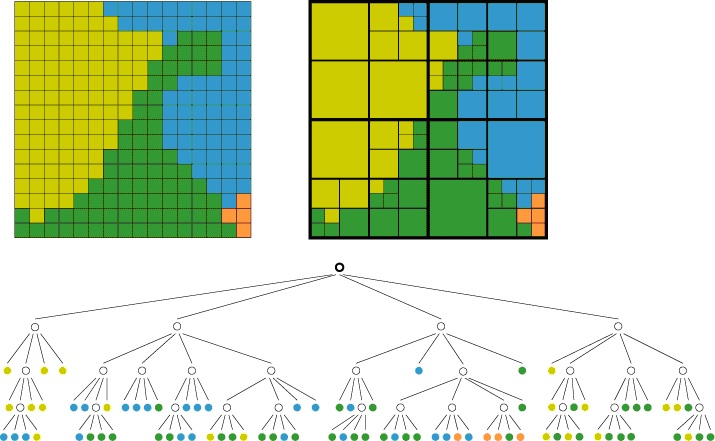
Négy-fa (Quad-tree)
A ma legelterjedtebb raszteres tömörítési eljárás. Ennél a módszernél már nem csak a soronkénti egyezőségeket tudjuk kihasználni a tárolásnál. A területet felosztjuk négy részre, majd az így kapott részeket addig osztjuk tovább, amíg az egyes részek homogén értékeket nem tartalmaznak. A kapott struktúrát egy kvadrális fában tároljuk (minden csomópontból további négy ág indulhat tovább), úgy hogy a cellaértékek a fa levelein találhatóak az ábrán látható módon. Az egyes csomópontok ágai az adott egység bontását az ÉNy-i saroktól az óramutató járásával egyező irányba adják meg.
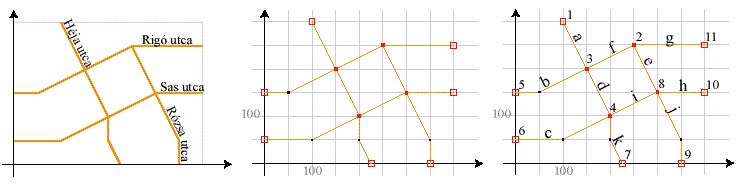
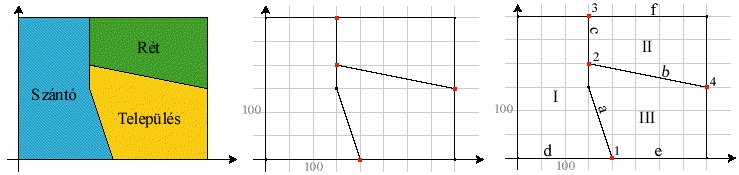
A vektoros alapú FIR-ek közös jellemzője, hogy a jelenségek térbeli elhelyezkedését pontok (pontszerű jelenségek), pontsorozatok (vonalas jelenségek), illetve záródó pontsorozatok (területi jelenségek) segítségével írjuk le. A pontok koordinátái mindig az aktuális leképezésnek megfelelően adjuk meg. A modell nem tartalmaz köríveket, és egyéb geometriai primitíveket ellentétben pl. a CAD rendszerekkel, hanem a méretaránynak megfelelő sűrűségű pontsorozatokkal közelíti azokat. A modellben minden ábrázolt jelenséghez tartozik egy egyedi azonosító, amely segítségével hivatkozhatunk a jelenségekre. Attól függően, hogy modellünk tartalmaz-e a jelenségek térbeli kapcsolatára utaló információkat, megkülönböztetünk, un. "spagetti" és topológikus modelleket. Előbbinél két jelenség térbeli kapcsolatáról csak koordinátáik vizsgálatával kaphatunk információkat, míg a topológikus modellek esetén a kapcsolatok nagy része leírt. Először vizsgáljuk meg a jóval egyszerűbb felépítésű spagetti modellt, de a későbbiekben általában feltételezzük a topológikus modell meglétét. A két modell összehasonlítását az azonos jelenségekre vonatkozó példák segítik.
Ebben a modellben nem foglalkozunk a jelenségek térbeli kapcsolataival, azaz nem tároljuk, hogy két terület határos-e, két vonal találkozik-e, stb. Ennélfogva a modell felépítése egyszerű, viszont a közös határokat, vonalakat többször kell tárolnunk, esetleges módosítás során előfordulhat, hogy több helyen ugyanazt a módosítást kell elvégezni. Ezt az adatmodellt használja, pl. a Mapinfo nevű FIR.
Pontszerű jelenségek ábrázolása spagetti modellben
Ha a jelenségeinket pontként ábrázoljuk, akkor úgy járunk el, hogy egy táblázatban tároljuk a jelenségek azonosítója mellett annak térbeli x és y koordinátáit.
Vonalas jelenségeket x;y koordinátapárok sorozatával írhatjuk le. A vonalak keresztezhetik egymást, innen a spagetti elnevezés. Az egész egy nagy tál spagettire (vagy makarónira - ízlés szerint) emlékeztet, amelyben a tészták egymáson keresztül-kasul tekeregnek.
Területi jelenségek ábrázolása spagetti modellben
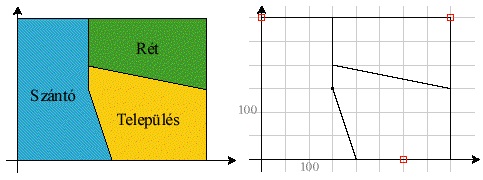
A területi jelenségek ábrázolása sokban hasonlít a vonalas jelenségek ábrázolására, azzal a különbséggel, hogy a leírt vonal záródik, az első, illetve az utolsó koordinátája megegyezik. Megfigyelhetjük a modell egyik hiányosságát, hogy a közös határvonalakat több helyen is tárolni kell. Így ha pl. két terület közös határvonala változik, nem elég egy helyen módosítani a koordinátákat.
Topológikus modell
Ebben a modellben a térbeli kapcsolatok leírása is igen nagy hangsúlyt kap. A topológia létrehozása, és karbantartása bonyolult feladat, az adatok geometriai minőségével szemben magasak az igények (pl. vonalak pontos csatlakozása). Cserébe viszont a tárolási költségek radikálisan lecsökkenhetnek, és a FIR műveletek sokkal bővebb tárháza áll rendelkezésünkre, mint a spagetti modellben. Ezt a modellt használják. pl. Arc/Info, TNT Mips.
Pontszerű jelenségek ábrázolása topológikus modellben
A pontszerű jelenségek tárolás hasonlóképpen történik, mint a spagetti modellben. Minden pont x;y koordinátáját tároljuk egy táblázatban.
Vonalas jelenségek ábrázolása topológikus modellben
A vonalak ábrázolásánál a legfontosabb kikötés, hogy két vonal nem keresztezheti egymást. A vonalak csomópontokban (node) végződnek. Attól függően, hogy egy csomópontból hány vonal indul ki megkülönböztetünk lógó csomópontokat (1 vonal indul), pszeudo csomópontokat (2 vonal indul), illetve normál csomópontokat.(3 vagy annál több vonal indul). A lógó csomópont előfordulhat pl. utcahálózat zsákutcájának végpontján. A pszeudo-csomópont az önmagukba záródó vonalak esetén fordul elõ pl. záródó szintvonalaknál, de jelenlétének lehetnek technikai okai is (pl. az ARC/Info egy vonalon csak 500 töréspontot engedélyez, és ezt túllépve automatikusan egy pszeudo csomópontot helyez el a vonalon). Megjelenik egy topológiákat tartalmazó táblázat, az un. vonal-csomópont topológia (arc-node topology). Ez tartalmazza, hogy melyik csomópontban melyik vonalak találkoznak. (pl. egy utcahálózatnál a kereszteződésekből kiinduló utcákat. Így pl. könnyen megmondhatjuk, hogy melyik utca melyiket keresztezi.)
Területi jelenségek ábrázolása topológikus modellben
A topológikus modellben minden vonalakkal határolt zárt területet poligonként értelmezünk. Két új topológiát tartalmazó táblázatot alkalmazunk: poligon-vonal topológiát (polygon-arc topology) és a szomszédsági topológiát. Ez előbbi tartalmazza, hogy melyik poligont melyik vonalak határolják, utóbbi pedig, hogy a vonalak jobb illetve bal oldalán mely poligonok találhatóak.