Superposition and interference
| What happens when two (or more) waves meet? As you can see in the image to the left, they will create a complex pattern in space and time depending on the phase difference between them. This pattern can be quantified using the principle of superposition. |
Principle of superposition
If two or more waves are moving through a medium, the resultant value of the wave function at any point is the algebraic sum of the values of the wave functions of the individual waves. \[y\left(x, t\right) = y_1\left(x, t\right) + y_2\left(x, t\right) + \ldots = \sum\limits_i{y_i\left(x, t\right)}\]
Interference and coherence
If waves that meet have similar waveforms and the phase difference between them is constant everywhere and at any time, their superposition will result in a constant pattern. We call this process interference. The capacity of waves to produce interference is called coherence. For instance, when we poke the surface of the water with two fingers, there will be interference if we poke in sync with the two fingers; in this case, the resultant waves are coherent. If the two fingers poke randomly and independently of each other, there will be no interference and the waves are not coherent.
Interference as a function of phase difference
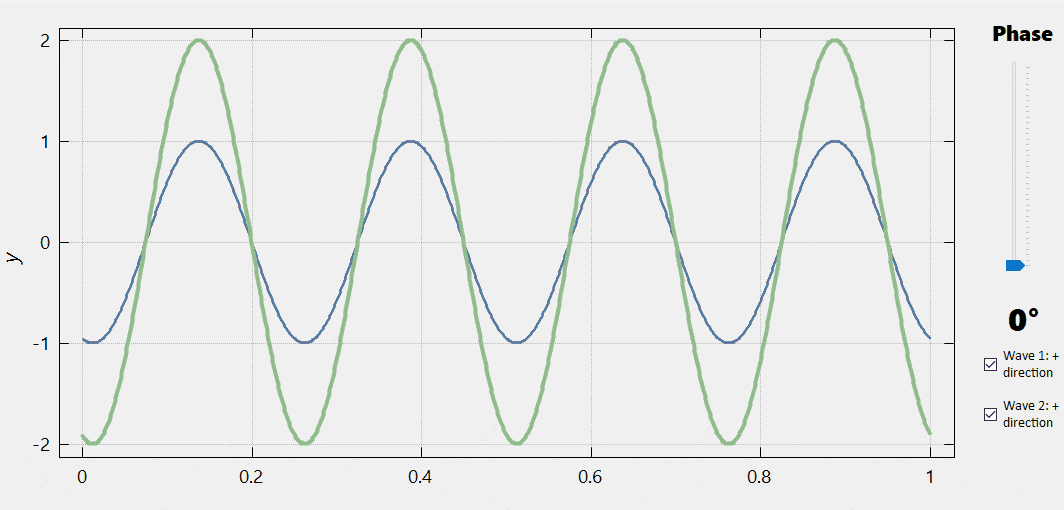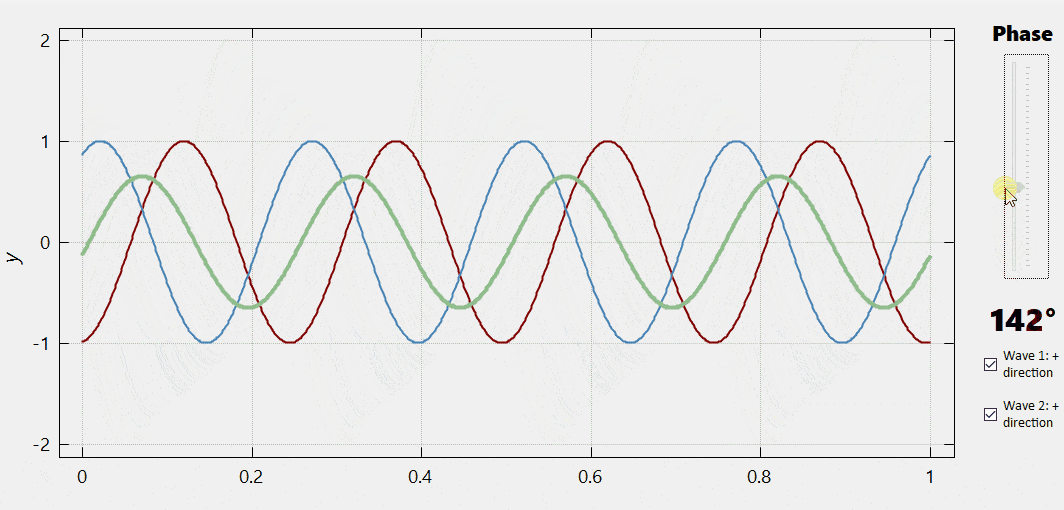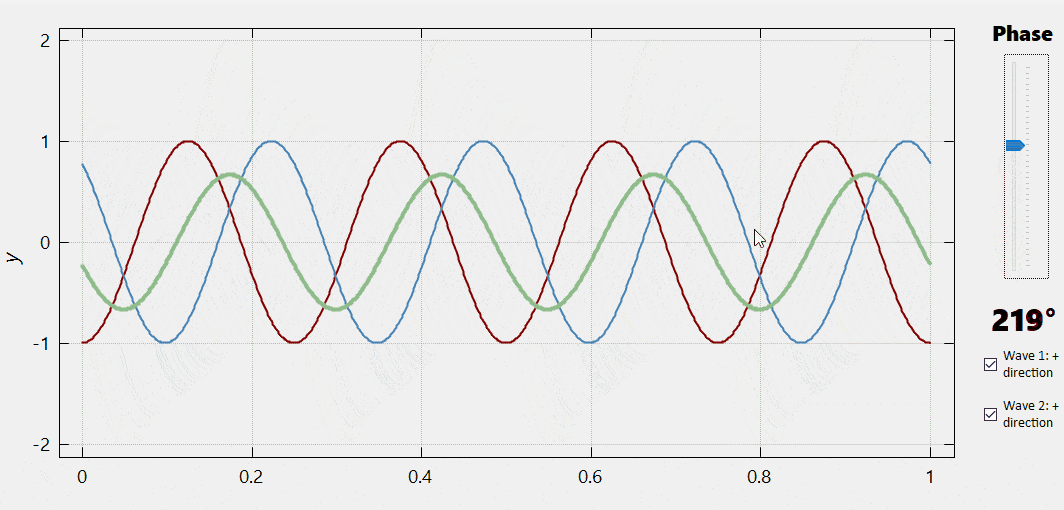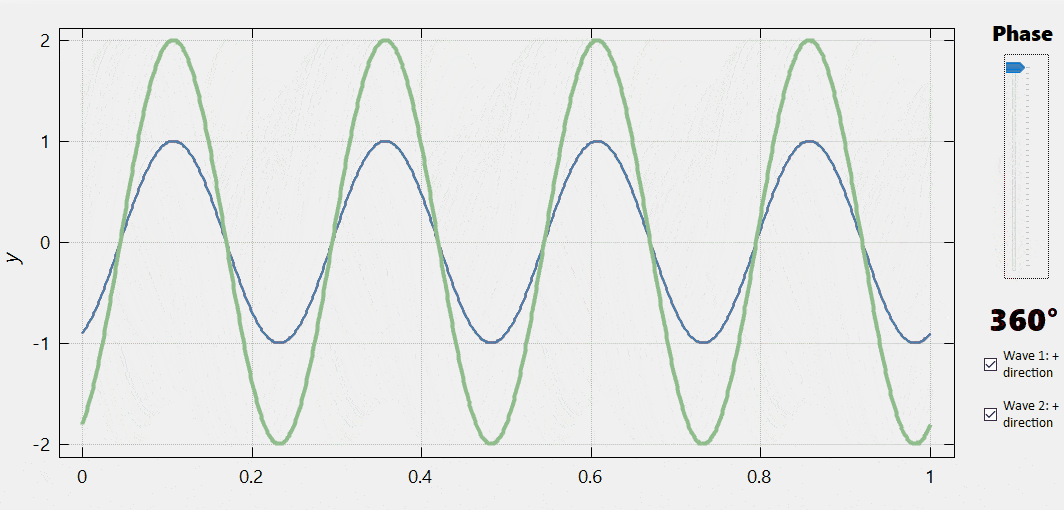 |
In the figure in the left, we can observe the interference between two identical waves for different values of the phase difference between them (varied using the slider). As we can see, one extreme case is when the phase difference is zero. Here the two waves produce a new wave whose amplitude is the sum of those of the interfering waves. By contrast, when the phase difference is \(\pi\,\mathrm{rad} = 180°,\) the two waves cancel each other. In between, the amplitude of the resultant wave changes continuously depending on the phase difference. |
Constructive and destructive interference
Constructive interference
Constructive interference occurs when the waves superposing produce a resultant wave with the greatest possible amplitude. The requirement for constructive interference is that the two waves should meet in phase (crest to crest, trough to trough), the phase difference between them should be an even multiple of \(\pi\): \(\phi = 2i \cdot \pi,\) where \(i\) is an arbitrary integer.
Destructive interference
Destructive interference occurs when the waves superposing produce a resultant wave with the least possible amplitude. The requirement for destructive interference is that the two waves should meet in opposite phase (crest to trough), the phase difference between them should be an odd multiple of \(\pi\): \(\phi = (2i + 1) \cdot \pi,\) where \(i\) is an arbitrary integer.
Proof: phase differences for constructive or destructive interference
Take two sinusoidal waves with the same amplitude \(A\) and angular frequency \(\omega\) which travel in the same direction and assume that the phase difference between them is constant for all positions and time instants: \(\phi.\)
The wave functions of the two waves:
\[y_1\left(x, t\right) = A \sin\left(k x - \omega t\right),\]
\[y_2\left(x, t\right) = A \sin\left(k x - \omega t + \phi\right).\]
According to the principle of superposition, the two waves will add up to a wave with the wave function
\[y\left(x, t\right) = y_1\left(x, t\right) + y_2\left(x, t\right),\]
\[y\left(x, t\right) = A \cdot \left[\sin\left(k x - \omega t\right) + \sin\left(k x - \omega t+ \phi\right)\right].\]
Let us use the following property of the sine function:
\[\sin\left(\alpha + \beta\right) = \sin\alpha\cos\beta + \cos\alpha\sin\beta.\]
When applied to our wave function, this will yield
\[y\left(x, t\right) = A \cdot \left[\sin\left(k x - \omega t\right) + \sin\left(k x - \omega t\right)\cos\phi +\cos\left(k x - \omega t\right)\sin\phi\right].\]
When the phase difference \(\phi\) is 0 (or an integer multiple of \(2\pi\)), \(\sin\phi = 0\) and \(\cos\phi = 1,\) and thus the expression will simplify to
\[y\left(x, t\right) = A \cdot \left[\sin\left(k x - \omega t\right) + \sin\left(k x - \omega t\right) \cdot 1 +\cos\left(k x - \omega t\right) \cdot 0 = 2A \sin\left(k x - \omega t\right)\right],\]
which corresponds to the greatest possible amplitude, that is, constructive interference.
When the phase difference \(\phi\) is \(\pi\) (give or take an integer multiple of \(2\pi\)), \(\sin\phi = 0\) and \(\cos\phi = -1,\) and thus the expression will simplify to
\[y\left(x, t\right) = A \cdot \left[\sin\left(k x - \omega t\right) + \sin\left(k x - \omega t\right) \cdot (-1) +\cos\left(k x - \omega t\right) \cdot 0\right] = 0,\]
which corresponds to the least possible amplitude, that is, destructive interference.
Interference as a function of path difference
|
In the figure, one can see two coherent, point-like wave sources and the resultant interference pattern. We expect sites of constructive interference where crest meets crest or trough meets trough, and destructive interference where crest meets trough. Picking one location with constructive interference, we can see that the crimson wave travelled a distance \(9\lambda / 4\) to reach this point, whilst the green one only \(5\lambda / 4.\) The path difference between them is exactly one wavelength. To reach the location with destructive interference marked in the figure, the crimson wave travelled \(5\lambda / 4,\) whilst the green one \(7\lambda / 4.\) The path difference between them is half the wavelength. |
We can generalise this observation and express the phase difference between waves in terms of path difference:
\[y_1\left(x, t\right) = A \sin\left(k x - \omega t\right),\]
\[y_2\left(x, t\right) = A \sin\left(k x - \omega t + \phi\right) = A \sin\left(k x + k \frac{\phi}{k} - \omega t\right) = A \sin\left(k \left[x + \frac{\phi}{k}\right] - \omega t\right).\]
This way, phase difference can be expressed as a path difference \(\Delta x = \frac{\phi}{k}\):
\[y_2\left(x, t\right) = A \sin\left(k \left[x + \Delta x\right] - \omega t\right).\]
Constructive interference will take place when the phase difference is an even multiple of \(\pi\):
\[\phi = 2i \cdot \pi \quad\Rightarrow\quad \Delta x = \frac{\phi}{k} = \frac{2 i \pi}{2\pi / \lambda} = 2 i \cdot \frac{\lambda}{2}.\]
Destructive interference will take place when the phase difference is an odd multiple of \(\pi\):
\[\phi = (2i + 1) \cdot \pi \quad\Rightarrow\quad \Delta x = \frac{\phi}{k} = \frac{(2 i + 1) \pi}{2\pi / \lambda} = (2 i + 1) \cdot \frac{\lambda}{2}.\]
Constructive interference v destructive interference: summary
Constructive interference
There are two ways to decide whether the interference between two waves will be constructive:- the phase difference between the two waves is an even multiple of \(\pi\);
- the path difference between the two waves is an even multiple of the half wavelength \(\frac{\lambda}{2}\).
Destructive interference
There are two ways to decide whether the interference between two waves will be destructive:- the phase difference between the two waves is an odd multiple of \(\pi\);
- the path difference between the two waves is an odd multiple of the half wavelength \(\frac{\lambda}{2}\).
