Standing waves
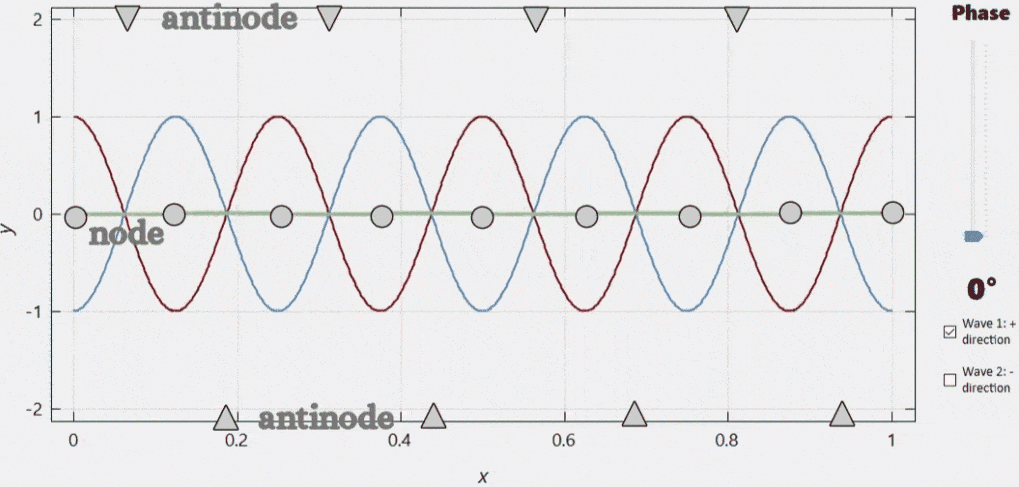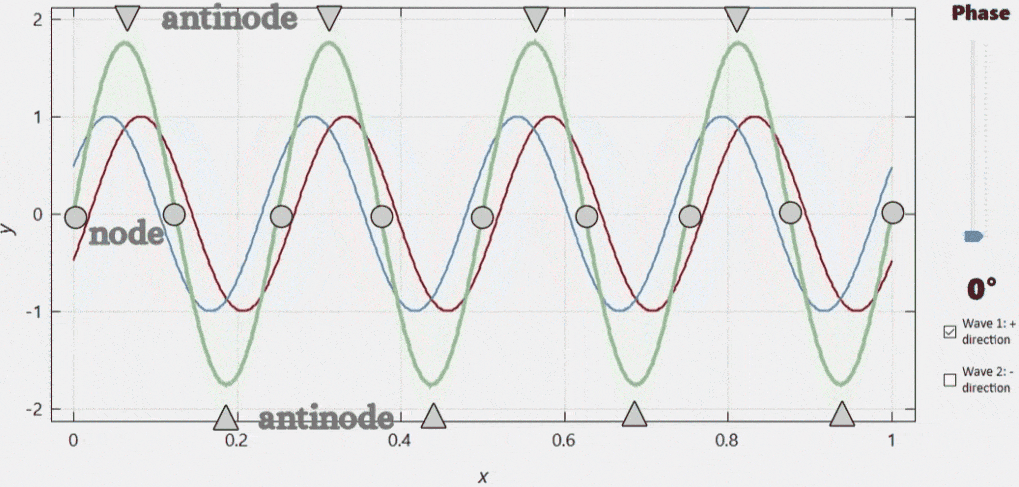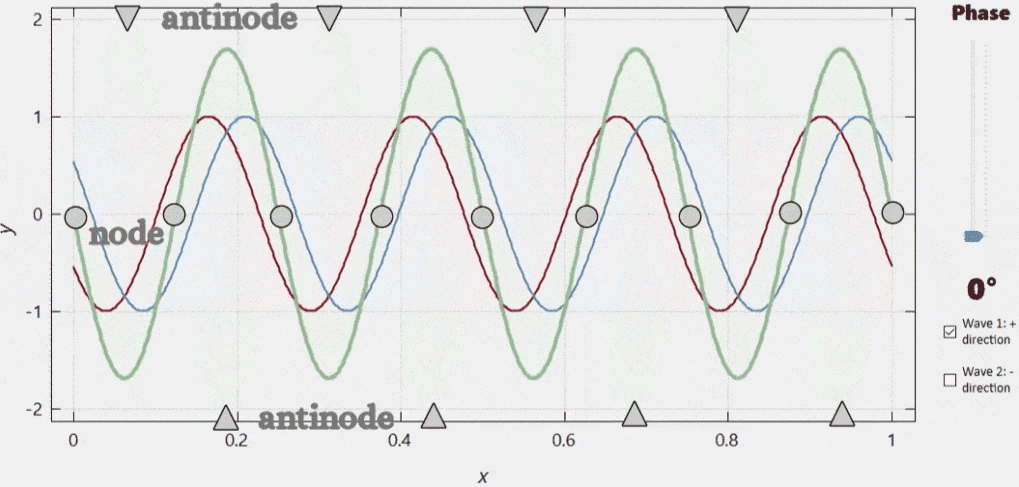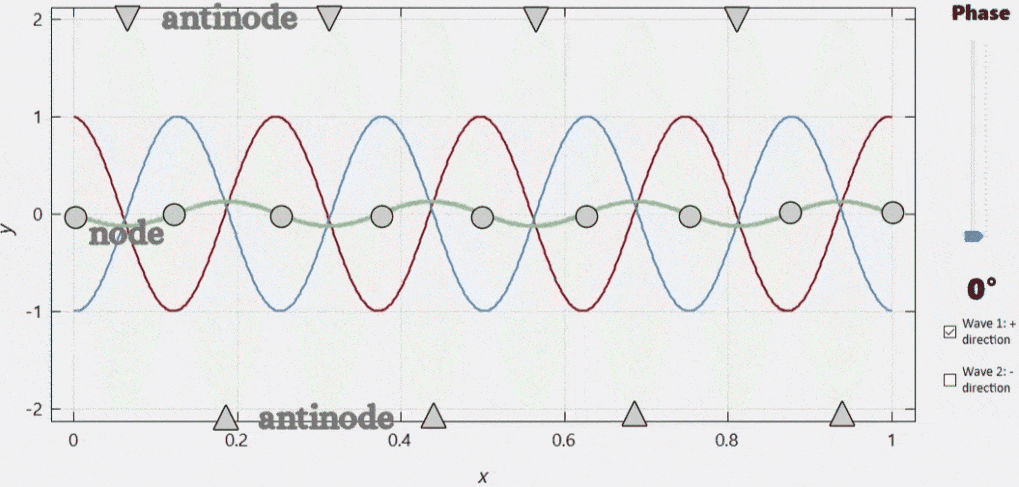 |
When two similar waves travelling in opposite directions are superposed, the result will be a wave that does not travel at all but oscillates in place. Such waves are called standing waves. Where the standing wave has a maximum at any given moment, there will always be a maximum or a minimum at any other time. We call these locations antinodes. Conversely, there are locations where the displacement is zero at any given moment. These sites are called nodes. |
Nodes occur at positions which meet the condition \[x = i \cdot \frac{\lambda}{2}.\]
The distance between adjacent nodes is \(\frac{\lambda}{2}.\)
Antinodes are found at positions \[x = (2 i + 1) \cdot \frac{\lambda}{4}.\]
The distance between adjacent antinodes is \(\frac{\lambda}{2},\) whilst a node and an adjacent antinode are separated by a distance \(\frac{\lambda}{4}.\)
Quantitative description of the formation of standing waves
Consider two waves with the same amplitude and frequency, travelling in the same medium in opposite directions:
\[y_1\left(x, t\right) = A \sin\left(k x - \omega t\right),\]
\[y_2\left(x, t\right) = A \sin\left(k x + \omega t\right).\]
The superposition of these waves will result in a wave function
\[y\left(x, t\right) = y_1\left(x, t\right) + y_2\left(x, t\right),\]
\begin{eqnarray*} y\left(x, t\right) & = & A \sin\left(k x - \omega t\right) + A \sin\left(k x + \omega t\right) =\\ & = & A \left[\sin\left(kx\right)\cos\left(\omega t\right) - \cos\left(kx\right)\sin\left(\omega t\right)\right. +\\ & + & \left.\sin\left(kx\right)\cos\left(\omega t\right) + \cos\left(kx\right)\sin\left(\omega t\right)\right] = \\ & = & 2 A \sin\left(kx\right)\cos\left(\omega t\right).\\ \end{eqnarray*}
This formula reflects that the resulting wave will not travel, but will oscillate in place with an amplitude depending on the position: \[y\left(x, t\right) = A(x) \cos\left(\omega t\right),\] where the position-dependent amplitude \(A(x)\) is \[A(x) = 2 A \sin\left(kx\right).\] Standing waves can form when a wave meets its own reflexion.
Nodes are, by definition, are locations where the displacement is always zero: \[A(x) = 2 A \sin\left(kx\right) = 0.\]
This happens when \[\sin\left(kx\right) = 0,\]
\[k x = i \pi,\ \mathrm{where}\ i \in \left\{0, 1, 2, 3, \ldots\right\},\] \[\frac{2 \pi}{\lambda} x = i \pi.\]
So nodes occur at positions which meet the condition \[x = i \cdot \frac{\lambda}{2}.\]
Antinodes are locations with maximum amplitude: \[A(x) = 2 A \sin\left(kx\right) = \pm 2 A.\]
This occurs at \[\sin\left(kx\right) = \pm 1,\] \[k x = (2 i + 1) \frac{\pi}{2},\ \mathrm{where}\ i \in \left\{0, 1, 2, 3, \ldots\right\},\]
\[\frac{2 \pi}{\lambda} x = (2 i + 1) \frac{\pi}{2}.\]
So antinodes occur at positions which meet the condition \[x = (2 i + 1) \cdot \frac{\lambda}{4}.\]
Standing waves on a string
|
When a string is plucked, a wave will form, and will eventually be reflected from a fixed end of the string. The original wave and the reflected wave will create standing waves. Since several reflexions are possible, several standing waves with different wavelength may arise and combine along the string. We call these the normal modes of the string. One condition that all these standing waves must meet is that the ends of the strings are fixed, so these must be nodes. The longest-wavelength standing wave must have two nodes, those at the fixed ends, and a single antinode in between (see panel 1 of the figure). In view of the considerations on nodes and antinodes above, this means that \[\frac{\lambda_0}{2} = L, \Rightarrow \lambda_0 = 2 L.\] The longest wavelength \(\lambda_0\) corresponds to the lowest frequency \(f_0\) (see the formula for wave speed): \[f_0 = \frac{v}{\lambda_0} = \frac{v}{2L}.\] We call this lowest frequency the fundamental frequency. |
The next normal mode is one with an additional node between the endpoints (see panel 2). For this one,
\[\lambda_1 = L, \Rightarrow f_1 = \frac{v}{L}.\]
The third has two additional nodes between the endpoinds (see panel 3):
\[\frac{3\lambda_2}{2} = L, \Rightarrow \lambda_2 = \frac{2 L}{3},\]
and
\[f_2 = \frac{v}{\lambda_2} = \frac{3v}{2L}.\]
We can generalise these findings and say that if a mode has \(n\) additional nodes besides the obligatory nodes at the endpoints, its wavelength will be
\[\lambda_n = \frac{2 L}{n + 1},\]
and the associated frequency will be
\[f_n = \frac{(n + 1)v}{2L} = (n + 1)f_0.\]
We can see that all the higher frequencies (which we call overtones) are integer multiples of the fundamental frequency \(f_0.\)
Standing waves in pipes
|
In air columns within pipes, similar standing waves may form. Here the conditions on endpoints may vary depending on whether they are open or closed. At closed ends, the air cannot move longitudinally, so closed ends must be displacement nodes. By contrast, open ends allow the air move freely, so they are bound to be displacement antinodes. Using a similar logic to the one above, we can arrive at similar formulae for any combination of open and closed ends. In all these, the frequencies of the overtones remain integer multiples of the fundamental frequency. |