Szerzők
Lektorálta: Orosz László, Budapesti Műszaki és Gazadaságtudományi Egyetem, TTK, Fizika Tanszék
Tartalom
- Előszó
- 1. Mechanika
- Kinematika
- A vektorszkóp
- Egyenes vonalú egyenletes mozgás
- Egyenes vonalú egyenletesen változó mozgás
- Harmonikus rezgőmozgás
- Két egyirányú és egyenlő frekvenciájú harmonikus rezgés összetevése
- Két egyirányú, közel egyenlő frekvenciájú harmonikus rezgés összetevése
- Ferde hajítás
- Egyenletes körmozgás
- Kapcsolat a körmozgás és a rezgőmozgás között
- Két egymásra merőleges harmonikus rezgés összetevése
- Pontszerű testek dinamikája
- Pontrendszerek dinamikája
- Merev test dinamikája
- Mechanikai jelenségek egymáshoz képest mozgó vonatkoztatási rendszerekben
- Nyugvó folyadékok mechanikája
- Rezgéstan
- A Pohl-féle készülék
- Harmonikus forgási rezgések vizsgálata Pohl-féle készülékkel
- Csillapított forgási rezgések vizsgálata Pohl-féle készülékkel
- Kényszerrezgés vizsgálata Pohl-féle készülékkel
- A rezgések kialakulásának feltételei, anharmonikus rezgések vizsgálata Pohl-féle készülékkel
- Kényszerrezgés ingákkal
- Hullámtani kísérletek vízhullámokkal
- Vízhullámok visszaverődése síkfelületről
- Vízhullámok visszaverődése görbült felületről
- Vízhullámok törése síkfelületen
- Vízhullámok törése görbült felületen, lencsék
- Hullámok interferenciája
- Vízhullámok elhajlása
- Vízhullámok szórása
- Felbontóképesség szemléltetése vízhullámokkal
- Vízhullámok diszperziója
- 2. Optika
- Kísérletek a fizikai fénytan témaköréből
- Fény-anyag kölcsönhatás
- A fény hullámtermészetű, kölcsönhatásra képes energiaáramlás
- Diszperzió (összetett és monokromatikus fény)
- Tyndall jelenség, a koherens fényszórás függése különböző paraméterektől
- A koherens fényszóródás típusai, fényszóródási jelenségek környezetünkben
- Színes oldatok, színszűrők fényelnyelése
- Környezetünk színei
- 3. Hat egyszerű eszközökkel elvégezhető mérési feladat
Az egyetemeken és főiskolákon folyó természettudományi illetve műszaki alapszakok bevezető fizika kurzusainak fontos részét képezik az előadásokon bemutatott kísérletek, melyek egyrészt megkönnyítik a hallgatók számára a fizikai törvények megértését, másrészt az előadást is színesebbé, érdekesebbé teszik. Sajnos az előadásokon rendszerint nincs lehetőség a kísérletek többszöri ismétlésére, pedig tapasztalataink szerint a hallgatóság egy jelentős része igényelné. A levelező tagozaton folyó képzés esetében az előadások óraszáma a nappali tagozatos képzés óraszámának fele, harmada. Ebből következően a nappali tagozat előadásain bemutatott kísérletek töredékét láthatják csak a levelező tagozatos hallgatók.
Ebben a helyzetben úgy gondoltuk, hogy az előadásokon látható kísérletek egy részét filmre vesszük, magyarázattal, animációkkal látjuk el, és a hallgatóság számára hozzáférhetővé tesszük az interneten. Reméljük, hogy az alább olvasható, nézhető digitális tananyag a fenti célok elérését segíti. Mivel ez a digitális tananyag a bevezető egyetemi fizika kurzusokhoz készült, így a bemutatott kísérletek jelentős része kapcsolódik a középiskolai fizika órák témáihoz is. Ennél fogva a középiskolai fizikatanárok és a fizika iránt érdeklődő diákok is találhatnak a tananyagban számukra hasznos, érdekes információkat.
A kísérletek megtekintése:
A kísérleteket bemutató filmeket általában a Kísérlet feliratra kattintással nézhetjük meg, melyhez a Windows Media Player 11 használatát javasoljuk. Ha a jelenséget lassítva is szeretnénk megnézni, akkor a program Lejátszás menüpontjában a Lejátszási sebesség-nél a Lassú opciót állítsuk be. Sok esetben tanulságos, ha kockánként nézzük végig a film egy részét. Ekkor a Nézet menüpontban a Bővítmények-re kattintva a Lejátszási sebesség beállításai opciót választjuk. Indítsuk el a filmet, és annál a résznél, ahol kockánként szeretnénk megnézni, a Pillanat-állj gombbal állítsuk meg. Ezután a Következő képkocka gombra kattintva tudjuk kockánként nézni a filmet. Az Előző képkocka gombra kattintva visszafelé is meg tudjuk nézni a kísérletet.
Abban az esetben, ha egy kísérlet egynél több részből áll, akkor a kísérlet leírásában egy-egy aláhúzással megjelölt szóra kattintva indulnak a kísérleteket bemutató filmek.
Az animációk megtekintése:
Az animációkat általában a szövegben szereplő, aláhúzással is megjelölt animácó szóra való kattintással indíthatjuk. Ahol több animáció is kapcsolódik egy jelenséghez, ott az aláhúzott szavakra kell kattintani. Ebben az esetben is a Windows Media Player11 használatát javasoljuk.
A szerzők
Jelen digitális tananyag a Tananyagfejlesztés és tartalomfejlesztés különös tekintettel a matematikai, természettudományi, műszaki és informatikai (MTMI) képzésekre című projekt (TÁMOP 4.1.2-08/1/A) keretében készült.

A projekt az Európai Unió támogatásával, az Európai Szociális Alap társfinanszírozásával valósult meg.
Tartalom
- Kinematika
- A vektorszkóp
- Egyenes vonalú egyenletes mozgás
- Egyenes vonalú egyenletesen változó mozgás
- Harmonikus rezgőmozgás
- Két egyirányú és egyenlő frekvenciájú harmonikus rezgés összetevése
- Két egyirányú, közel egyenlő frekvenciájú harmonikus rezgés összetevése
- Ferde hajítás
- Egyenletes körmozgás
- Kapcsolat a körmozgás és a rezgőmozgás között
- Két egymásra merőleges harmonikus rezgés összetevése
- Pontszerű testek dinamikája
- Pontrendszerek dinamikája
- Merev test dinamikája
- Mechanikai jelenségek egymáshoz képest mozgó vonatkoztatási rendszerekben
- Nyugvó folyadékok mechanikája
- Rezgéstan
- A Pohl-féle készülék
- Harmonikus forgási rezgések vizsgálata Pohl-féle készülékkel
- Csillapított forgási rezgések vizsgálata Pohl-féle készülékkel
- Kényszerrezgés vizsgálata Pohl-féle készülékkel
- A rezgések kialakulásának feltételei, anharmonikus rezgések vizsgálata Pohl-féle készülékkel
- Kényszerrezgés ingákkal
- Hullámtani kísérletek vízhullámokkal
- Vízhullámok visszaverődése síkfelületről
- Vízhullámok visszaverődése görbült felületről
- Vízhullámok törése síkfelületen
- Vízhullámok törése görbült felületen, lencsék
- Hullámok interferenciája
- Vízhullámok elhajlása
- Vízhullámok szórása
- Felbontóképesség szemléltetése vízhullámokkal
- Vízhullámok diszperziója
A Kinematika, a Pontszerű testek dinamikája és a Pontrendszerek dinamikája című fejezetekben bemutatott kísérleteknél fontos, hogy ne csak kvalitatívan tudjuk vizsgálni a testek mozgását, hanem rendelkezzünk minél pontosabb információval a testek helyzetéről, sebességéről, gyorsulásáról a kísérlet időtartama alatt. Ezt a lehetőséget biztosítja számunkra a vektorszkóp.
A vektorszkóp egy számítógép által vezérelt mérőeszköz, mellyel mozgó testek pályáját lehet nyomon követni. A rendszer az alább ismertetendő módon meghatározza a testek koordinátáit egymást követő időpillanatokban, és így megkapjuk a mozgás pályáját, azaz az r(t)=[x(t), y(t), z(t)] helyvektort az idő függvényében. Innen származik az eszköz elnevezése is. A mérőrendszerhez tartozó számítógép monitorján a méréssel egy időben nemcsak a test helyvektorának, hanem sebességvektorának és gyorsulásvektorának pillanatnyi értékei is kirajzoltathatók. Tekintettel arra, hogy a következőkben csak egydimenziós mozgásokat fogunk vizsgálni, így a vektorszkóp működését is erre az esetre vonatkozóan ismertetjük.
A vektorszkóp négy fő egységből áll: egy nyugalomban lévő, infravörös jelet kisugárzó és ultrahangot vevő toronyból (1.1.1.a ábra), a mozgó testre felhelyezett, infravörös jelet vevő és ultrahangot kisugárzó gombból (1.1.1.b ábra), a toronnyal összekötött adatgyűjtő egységből, melyet egy számítógép vezérel a V-scope program segítségével.
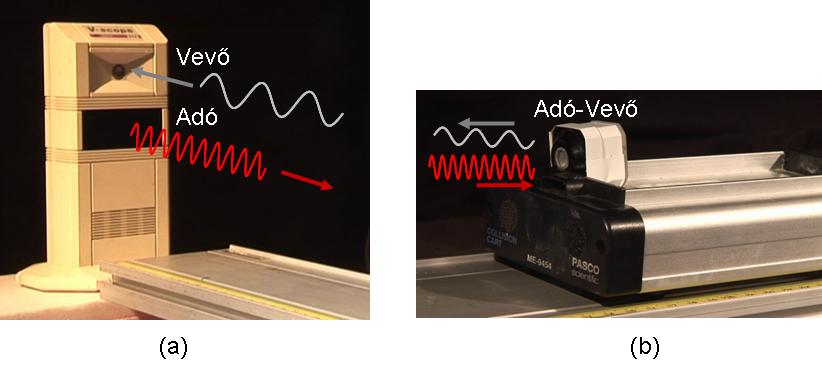
1.1.1. ábra A vektorszkóp adó- és vevőegységeinek elhelyezése
A mérés kezdetén a számítógép aktiválja a tornyot, melynek eredményeképp a torony egy rövid időtartamú infravörös jelet bocsát ki. Amikor ez a jel eléri a gomb vevőegységét, az adóegysége ultrahanghullámot bocsát ki. A torony érzékeli a gomb válaszjelét, és elektromos impulzusokká átalakítva továbbítja az adatgyűjtő egységnek, ahonnan az adatok a számítógépre kerülnek. Ekkor mérésre kész állapotba került az eszköz.

1.1.2. ábra A vektorszkóp helymeghatározási módszere
A mérést elindítva, a torony adott időközönként infravörös jeleket bocsát ki, amire a mozgó testen lévő gomb ultrahanghullámú jelekkel válaszol. A torony által kibocsátott infravörös hullámok a mozgó testhez rögzített gombot τ1 idő alatt érik el (1.1.2. ábra). A gomb válaszjele, az ultrahanghullám a torony vevőegységéhez τ2 idő alatt ér el. Míg az infravörös hullámok fénysebességgel, addig az ultrahanghullámok ehhez képest jelentősen kisebb sebességgel terjednek a levegőben, így a toronyból az infravörös jel kibocsátása és a gombtól hozzá visszaérkezett válaszjel detektálása között eltelt idő: τ ≈ τ2. Ezen idő megmérésével a program kiszámolja az x = vUH τ összefüggés alapján, hogy a toronytól adott időpillanatban a gomb milyen távolságra van, ahol vUH az ultrahanghullám terjedési sebessége levegőben. A toronyban elhelyezett hőmérő lehetővé teszi az ultrahang sebességének hőmérsékleti korrekcióját is.
A test két egymás utáni, t1 és t2 = t1+ Δt mérési időpont közötti átlagsebességét a program az egymást követő x1 és x2 értékek közti különbség és a két mérés között eltelt idő hányadosából határozza meg, azaz vátl = (x2 - x1)/Δt. Mennél rövidebbek a Δt időközök, annál jobban közelítik a mért átlagsebesség értékek a testnek a mérések pillanatában elért sebességét. Ha ismerjük a pillanatnyi sebességet az egymást követő időpontokban, akkor hasonló módon a gyorsulás is meghatározható. A mintavételek közötti Δt időtartamot 10-100 ms között állíthatjuk be.
Kísérlet:Egy kiskocsit egy egyenes és vízszintes alumínium sínen meglökünk. A kocsi fém kerekei és a sín között fellépő súrlódás gyakorlatilag elhanyagolható. A mozgás során a kocsi helyzetét és sebességét vektorszkóp segítségével határozzuk meg. A vektorszkóp tornyát az 1.1.2. ábrán látható módon a sín végéhez tesszük, míg a gombot a kiskocsira helyezzük.
Megfigyelés: A mérés kezdetekor a sínen a kocsi az x0=1,8 m pozíciónál van, a kezdősebessége 0 m/s (1.1.3. ábra). t = 0,8 s-kor meglökjük a kocsit, és a lökés hatására a sebessége -0,7 m/s-ra változik. Mivel a vektorszkóp számára a mozgásirány akkor pozitív, ha a toronytól távolodik a kocsi (1.1.2. ábra), így a sebességérték negatív előjele arra utal, hogy a kocsi a torony felé közeledik a mérés közben. A kocsit magára hagyva a sebessége állandó értékű marad, azaz a v(t) sebesség-idő grafikon egy vízszintes egyenes. A kocsi helyzetét leíró x(t) grafikon a lökés utáni időponttól egy -0,7 m/s meredekségű egyenes.
Ha jobban megnézzük az 1.1.3. ábrát, akkor úgy tűnik, mintha a kocsi sebessége a kezdeti nyugalmi állapotot jellemző 0 m/s-ról előbb kezdene el nőni, minthogy a kocsi megmozdulna. Ennek az oka, hogy amikor meglökjük a kocsit, akkor kezdetben kicsit változik a helykoordinátája az egymást követő mérési időpontokban a későbbi értékekhez képest, így a grafikonon nem igazán látható ez a változás. Ezzel szemben a kocsinak a lökés utáni sebességértékei a végsebességéhez képest nem olyan kicsi értékűek, ezért jól látható a sebesség növekedése már a kocsi meglökésének első pillanataiban is.
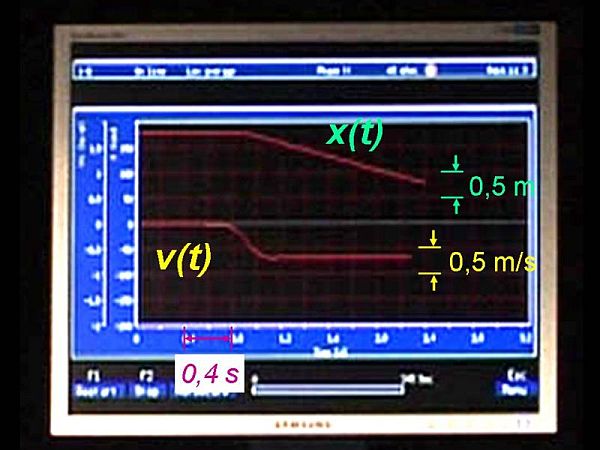
1.1.3. ábra A kocsi helyzetének és sebességének a vektorszkóp által mért értékei az idő függvényében
Példák egyenes vonalú egyenletes mozgásokra animációkkal
Ahhoz hogy a mozgó test helyzetének, sebességének és gyorsulásának időfüggését ábrázoló grafikonok alapján minél könnyebben el tudjuk képzelni a test mozgását, tekintsünk néhány animációt az egyenes vonalú egyenletes mozgásokkal kapcsolatban. A test vagy testek pályájához rögzítsük az x-tengelyt!
a) Animáció: Egy test az x 0 = 200 m helyzetből indul, és v 0 = 10 m/s egyenletes sebességgel mozog
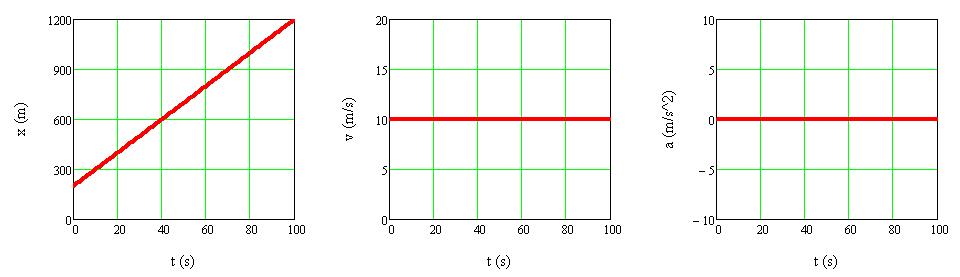
1.1.4. ábra A test helyzetének, sebességének és gyorsulásának időfüggését ábrázoló grafikonok
Egyenes vonalú egyenletes mozgás során a test helyzetét megadó x koordináta időfüggését az x(t) = v 0 t + x 0 függvény írja le, míg a sebességet egy állandó, de nem zérusértékű függvény, azaz v(t) = v 0 (1.1.4. ábra). Mivel a test sebessége időben nem változik, így a gyorsulás értéke végig zérus, azaz a(t) = 0.
b) Animáció: Két test azonos pontból (x 0P = x 0K = 0 m) indul, és azonos irányban mozognak egyenletes, de eltérő sebességgel (v 0K = 5 m/s, v 0P = 10 m/s )
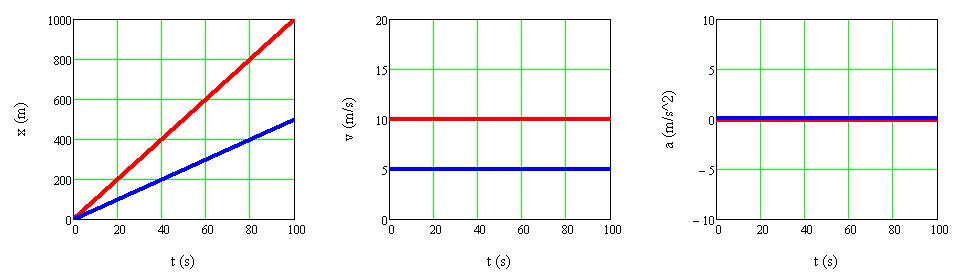
1.1.5. ábra A két test helyzetének, sebességének és gyorsulásának időfüggését ábrázoló grafikonok
Vegyük észre, hogy a kék testhez képest kétszer nagyobb sebességgel mozgó piros test helyzetét megadó x P (t) függvény meredeksége is kétszer nagyobb a kék test x K (t) függvényénél (1.1.5. ábra). Bár a testek sebessége eltérő, de időben nem változik, így mindkét test gyorsulása 0 m/s2.
c) Animáció: Két test különböző helyről (x 0P = 0 m, x 0K = 400 m) indul, és egyenletes, de eltérő sebességgel mozognak azonos irányban (v 0K = 5 m/s, v 0P = 10 m/s )
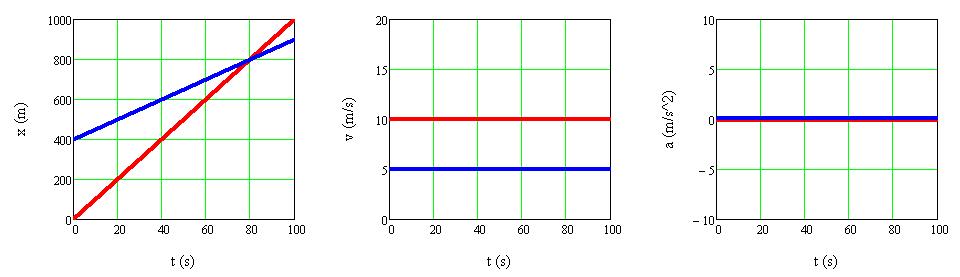
1.1.6. ábra A két test helyzetének, sebességének és gyorsulásának időfüggését ábrázoló grafikonok
A piros test a kék test mögül indul és nagyobb a sebessége a kék testénél, így a helyzetét megadó x P (t) függvény meredekebb az x K (t) függvénynél (1.1.6. ábra). t = 80 s-nál a piros test utoléri a kék testet, ekkor a két görbe metszi egymást, de ez nem jelenti azt, hogy ütköznek a testek. A sebesség és gyorsulás időfüggését mutató grafikonok megegyeznek a b) esetnél az 1.1.5. ábrán láthatóakkal.
d) Animáció: Két test különböző helyről (x 0P = 0 m, x 0K = 800 m) indul, és egyenletes, eltérő nagyságú és ellentétes irányú sebességgel mozognak (v 0K = -5 m/s, v 0P = 10 m/s )
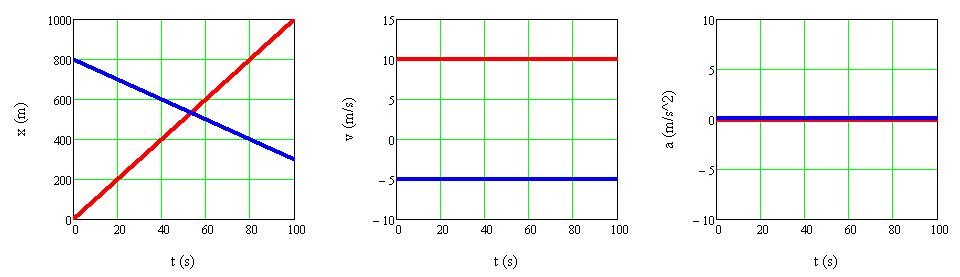
1.1.7. ábra A két test helyzetének, sebességének és gyorsulásának időfüggését ábrázoló grafikonok
Mivel a kék test a piros testtel szemben halad, és az x-tengely irányát úgy választottuk meg, hogy az a piros test mozgásának irányába mutasson, ezért a kék test sebessége negatív előjelű, és a helyzetét megadó x K (t) függvény meredeksége negatív (1.1.7. ábra). A két test x(t) függvénye t=53,3 s-nál metszi egymást, azaz ekkor találkoznak a testek, de ez nem jelenti azt, hogy ütköznek is. A gyorsulása mindkét testnek 0 m/s2, mivel a sebességük időben nem változik.
Kísérlet:Egy kiskocsit egy egyenes és vízszintes alumínium sínre helyezünk. A kiskocsihoz egy fonalat kötünk, melyet átvetünk a sín végén lévő csigán. A fonal másik végére 50 g tömegű nehezéket erősítünk. A mozgás során a kocsi sebességét és gyorsulását vektorszkóp segítségével határozzuk meg. A vektorszkóp tornyát a sínnek a csigával átellenes végéhez tesszük, míg a gombot a kiskocsira helyezzük.
Megfigyelés: Kezdetben a kocsit kézzel fogjuk, ekkor a sebessége és a gyorsulása is zérus. t = 0,4 s-kor elengedjük a kocsit. t = 0,8 s-tól a gyorsulás-idő grafikon egy vízszintes egyenes, azaz a kocsi gyorsulása állandó 0,8 m/s2 értékű (1.1.8. ábra). A kocsi sebessége az idővel lineárisan változik. A v(t) függvény meredeksége 0,8 m/s2, azaz megegyezik a gyorsulás értékével. Nyilvánvaló módon a valóságban pillanatszerűen nem nőhet meg a gyorsulás értéke, ezért a 0,4-0,8 s között látható egy átmeneti szakasz, ahol a gyorsulás folyamatosan változva vette fel végül az állandó értéket.
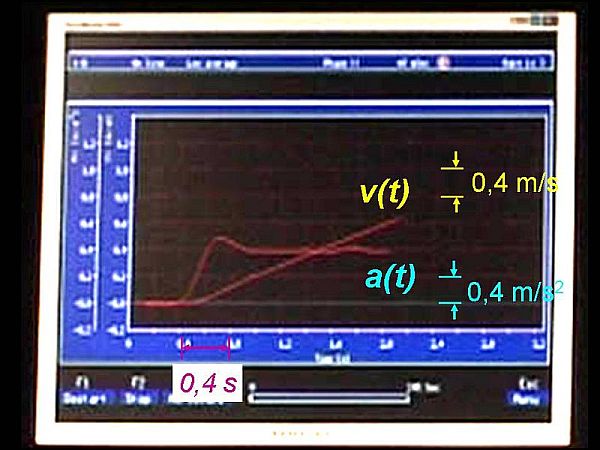
1.1.8. ábra A kocsi helyzetének és sebességének a vektorszkóp által mért értékei az idő függvényében
Példák egyenes vonalú egyenletesen gyorsuló mozgásokra animációkkal
A test pályájához rögzítsük az y-tengelyt úgy, hogy az origó a talajon van, és függőlegesen felfelé mutat a tengely!
a) Animáció: Egy testet 500 m magasból elejtünk
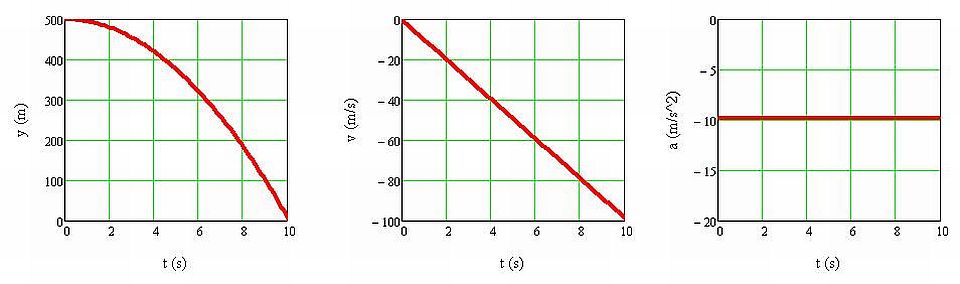
1.1.9. ábra 500 m magasból szabadon eső test helyzetének, sebességének és gyorsulásának időfüggését ábrázoló grafikonok
Látható, hogy a test helyzetét megadó y(t) függvény az egyenes vonalú egyenletes mozgással szemben most nem egy egyenes, hanem egy fél parabola, melynek az alakját az y(t) = -gt 2 /2 + y 0 egyenlet írja le (1.1.9. ábra), ahol g a nehézségi gyorsulás értéke (g = 9,81 m/s2). Fontos megjegyeznünk, hogy az y(t) grafikon nem a test által megtett utat, hanem a test helyzetét adja meg az idő függvényében. A test sebességének időfüggését ábrázoló v(t) függvény egy negatív meredekségű egyenes, mivel a mozgás iránya ellentétes az y-tengely irányával, azaz v(t) = -gt. A gyorsulás egy állandó érték, jelen esetben g. Az előjele negatív, mivel az y-tengely irányával ellentétes.
b) Animáció: Egy testet v 0 = 50 m/s sebességgel függőlegesen felfelé kilövünk
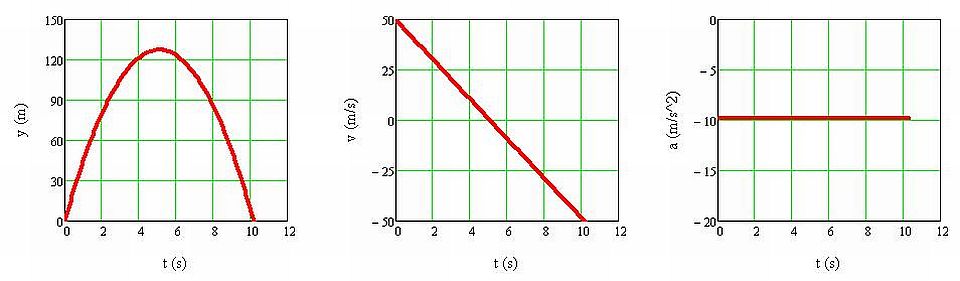
1.1.10. ábra Egy 50 m/s sebességgel függőlegesen felfelé kilőtt test helyzetének, sebességének és gyorsulásának időfüggését ábrázoló grafikonok
Ebben az esetben a test y(t) függvénye egy teljes parabola (1.1.10. ábra). Vegyük észre, hogy a test akkor éri el a pályájának csúcspontját, amikor a sebessége a kezdeti 50 m/s-ról 0 m/s-ra csökken le. Ezután a test zuhanni kezd, így az a) esethez hasonlóan a sebességének nagysága nő, és negatív előjelű lesz, mivel az y-tengellyel ellentétes irányban mozog. A gyorsulás végéig állandó értékű és negatív előjelű.
Az utolsó animációnál a test az előbbi esetektől eltérően vízszintes síkban, az x-tengely mentén mozog.
c) Animáció: Egy test 40 s-ig 10 m/s 2 gyorsulással mozog, majd a következő 40 s alatt a sebessége állandó. Végül mozgásának utolsó 20 másodpercében 20 m/s 2 -tel lassul
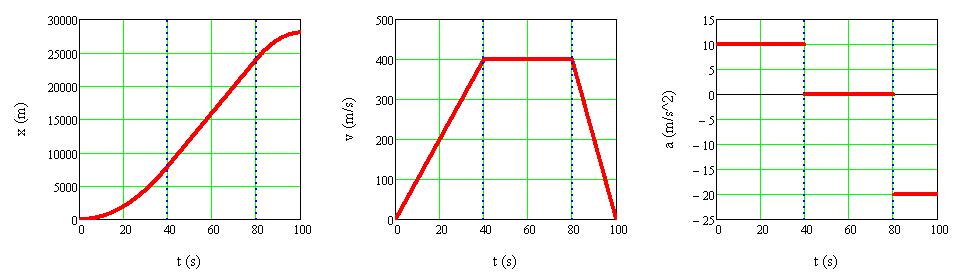
1.1.11. ábra A test helyzetének, sebességének és gyorsulásának időfüggését ábrázoló grafikonok
Az első 40 s alatt a testnek állandó a gyorsulása, ezért a sebesség-idő grafikonjának ezen része egy egyenes, amelynek a meredeksége éppen a gyorsulás értéke, azaz 10 m/s2 (1.1.11. ábra). A test helyzetét megadó x(t) függvény ebben az időtartományban pedig egy felfelé néző parabola, melynek a csúcsa a (0,0) pontban van.
A 40-80 s közötti tartományban a gyorsulás 0 m/s2, azaz a test sebessége állandó. A mozgás ezen szakaszában az x(t) függvény egy egyenes, melynek a meredeksége éppen a sebesség értéke, azaz 400 m/s.
Az utolsó 20 másodpercben fékezni kezd a test. A fékezés miatt a gyorsulás a mozgás irányával, az x-tengellyel ellentétes irányú, ezért negatív előjelű. A fékezés hatására a test sebessége csökken. Mivel fékezéskor a gyorsulás nagysága kétszer akkora, mint amekkora a gyorsításkor volt, ezért a sebesség-idő grafikon ebben a tartományban egy kétszer akkora meredekségű egyenes, mint amilyen a gyorsítási szakaszban volt. A test helyzetét megadó x(t) függvény pedig egy lefelé néző parabola.
Kísérlet: Egy rugóra felakasztunk egy testet és megvárjuk, amíg nyugalomba kerül. Ezután a testet függőleges irányban kitérítjük a nyugalmi helyzetéből és magára hagyjuk. Vizsgáljuk meg egy animáció segítségével, hogy hogyan mozog a test!
Megfigyelés: A test a függőleges tengely (y-tengely) mentén rezeg, két szélső helyzet között periodikusan ismétlődő mozgást végez (1.1.12. ábra). A test sebessége és gyorsulása is a kitéréshez hasonlóan szintén az időnek harmonikus függvénye, csak eltérő amplitúdóval és fázissal.
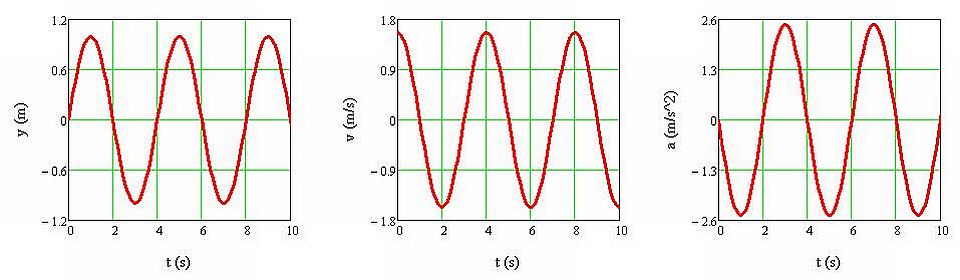
1.1.12. ábra A test helyzetének, sebességének és gyorsulásának időfüggését ábrázoló grafikonok. Paraméterek: A = 1 m, T = 4 s, φ = 0 rad
Magyarázat: Harmonikus rezgőmozgás esetében a kitérés az időnek harmonikus függvénye, azaz y(t) = Asin(ωt+φ), ahol A a maximális kitérés vagy más néven amplitúdó, ω a körfrekvencia és φ a kezdőfázis. A ω körfrekvencia és a rezgés T periódusideje közötti kapcsolat: ω=2π/T. Ha a φ értéke 0 radián, akkor a fenti y(t) kitérés-idő függvény esetében a t = 0 időpillanatban a test kitérése zérus, és a t = 0 után egy ideig a test felfelé mozog (1.1.12. ábra).
Harmonikus rezgés esetén a sebesség és a gyorsulás is az időnek harmonikus függvénye: v(t)=Aωcos(ωt+φ) és a(t)= -Aω 2 sin(ωt+φ).
Kísérlet: Vizsgáljuk meg animáció segítségével két egyirányú, azonos frekvenciájú és azonos amplitúdójú harmonikus rezgés összegét, melyek között nincs fáziskülönbség!
Megfigyelés: Az eredő rezgés frekvenciája és fázisa megegyezik az összeadandó rezgések frekvenciájával és fázisával, viszont az amplitúdója kétszer akkora (1.1.13. ábra).
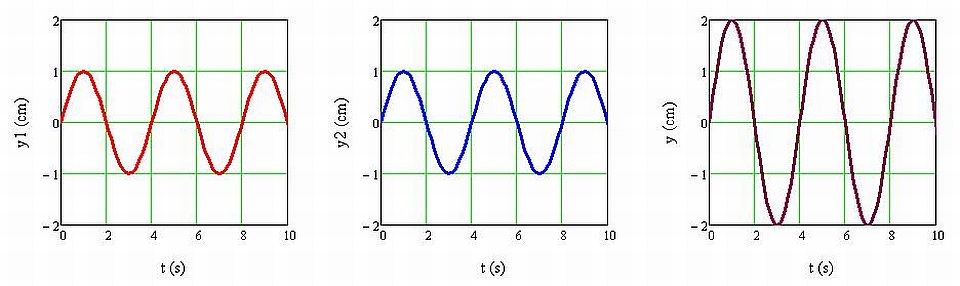
1.1.13. ábra Két egyirányú, azonos frekvenciájú, azonos amplitúdójú és azonos fázisú harmonikus rezgés (y1(t) és y2(t)), valamint az eredő rezgés (y(t)) kitérés-idő függvénye
Magyarázat: Általános esetben két egyirányú, azonos frekvenciájú rezgés kitérés-idő függvénye: y 1 (t) = A 1 sin(ωt+φ 1 ) és y 2 (t) = A 2 sin(ωt+φ 2 ).
Az eredő rezgés kitérés-idő függvénye: y(t) = y 1 (t)+y 2 (t) = Asin(ωt+φ), ahol A 2 =A 1 2 +A 2 2 +2A 1 A 2 cos(φ 2 -φ 1 ) és tgφ =(A 1 sinφ 1 + A 2 sinφ 2 )/( A 1 cosφ 1 + A 2 cosφ 2 ).
Jelen esetben A1 = A2 = 1 cm és φ2 = φ1 = 0 rad. Ekkor a fenti összefüggések alapján A = 2 cm és φ = 0 rad. Az összeadandó rezgések és az eredő rezgés periódusideje: T1=T2=T=4s.
Kísérlet: Vizsgáljuk meg animáció segítségével két egyirányú, azonos frekvenciájú és azonos amplitúdójú harmonikus rezgés összegét, melyek között a fáziskülönbség π!
Megfigyelés: Az eredő rezgés amplitúdója zérus (1.1.14. ábra).
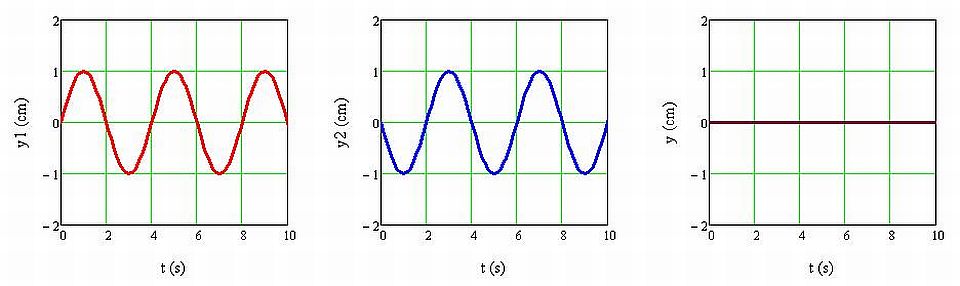
1.1.14. ábra Két egyirányú, azonos frekvenciájú, azonos amplitúdójú és ellentétes fázisú harmonikus rezgés (y1(t) és y2(t)), valamint az eredő rezgés (y(t)) kitérés-idő függvénye
Magyarázat: A fenti összefüggés alapján az eredő rezgés amplitúdója ebben az esetben A = 0 cm, tehát a két rezgés egymás hatását kioltja.
Kísérlet: Vizsgáljuk meg animáció segítségével két egyirányú, azonos frekvenciájú és eltérő amplitúdójú harmonikus rezgés összegét, melyek között a fáziskülönbség π!
Megfigyelés: Az előző esettel összevetve, most nincs kioltás, csak gyengítés. Az eredő rezgés amplitúdója a két rezgés amplitúdójának különbségével egyezik meg (1.1.15. ábra).
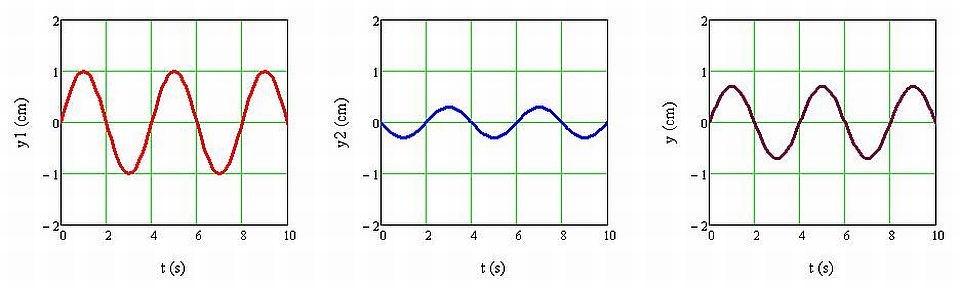
1.1.15. ábra Két egyirányú, azonos frekvenciájú, eltérő amplitúdójú és ellentétes fázisú harmonikus rezgés (y1(t) és y2(t)), valamint az eredő rezgés (y(t)) kitérés-idő függvénye
Magyarázat: A fenti összefüggések alapján és figyelembe véve, hogy A1 = 1 cm és A2 = 0,3 cm, valamint φ1 = 0 rad, φ2 = π rad, adódik, hogy A = A2-A1 = 0,7 cm és φ = 0 rad.
Kísérlet: Vizsgáljuk meg animáció segítségével két egyirányú, azonos amplitúdójú, de kissé eltérő frekvenciájú harmonikus rezgés összegét!
Megfigyelés: Amikor a két rezgés közel azonos (ellentétes) fázisban van, akkor az eredő rezgés amplitúdója nagyobb (kisebb) a két összetevő rezgés amplitúdójánál (1.1.16. ábra). Az eredő rezgés amplitúdója tehát időben periodikusan változik. Két maximumhely közötti időtartam 0,5 s, ami 2 Hz frekvenciának felel meg. Ez éppen a két rezgés frekvenciájának különbsége.
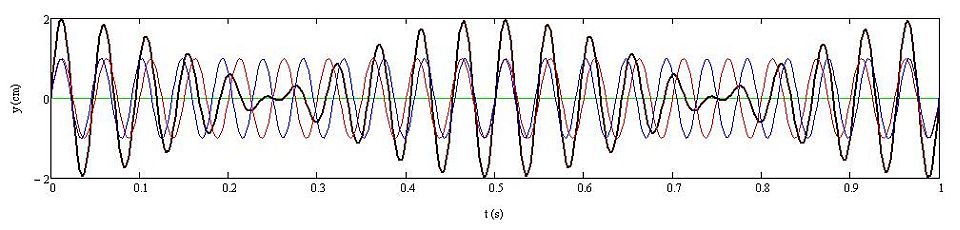
1.1.16. ábra Két egyirányú, azonos amplitúdójú, de kissé eltérő frekvenciájú harmonikus rezgés (y1(t) és y2(t)), valamint az eredő rezgés (y(t)) kitérés-idő függvénye. Paraméterek: A1= A2 = 1 cm, ν1 = 20 Hz, ν2 = 22 Hz, φ1 =φ2 = 0 rad
Magyarázat: A két rezgés kezdőfázisa a fenti animációnak megfelelően zérus, így a kitérés-idő függvényeik: y 1 (t) = Asin(ω 1 t) és y 2 (t) = Asin(ω 2 t). A két rezgés ω 1 és ω 2 körfrekvenciája csak kismértékben különbözik egymástól. Jelen esetben ω 2 >ω 1 . Az eredő rezgés kitérés-idő függvénye: y(t) = y 1 (t)+y 2 (t) = Asin(ω 1 t)+ Asin(ω 2 t), mely egyszerű átalakítás után az y(t) = 2Acos((ω1-ω2)t/2)sin((ω1+ω2)t/2) alakra hozható.
Vegyük észre, hogy a koszinusz-függvény argumentuma időben sokkal lassabban változik a szinusz-függvény argumentumához képest amiatt, hogy a két rezgés körfrekvenciájának értéke között kicsi a különbség. Így az eredő rezgést egy olyan színuszrezgésnek foghatjuk fel, melynek a körfrekvenciája a két rezgés körfrekvenciájának számtani közepe, az amplitúdója pedig időben viszonylag lassan ingadozik a 0 és a 2A érték között. Ezt a jelenséget lebegésnek nevezzük. A lebegés frekvenciája: νl= |ν2 - ν1|. A fenti paraméterekkel νl = 22- 20 Hz = 2 Hz.
Kísérlet: Vizsgáljuk meg animáció segítségével két egyirányú, kissé eltérő frekvenciájú és különböző amplitúdójú harmonikus rezgés összegét!
Megfigyelés: Az előző esethez hasonló megfigyeléseket tehetünk. A különbség annyi, hogy most az eredő rezgés amplitúdója nem csökken le zérusra sosem (1.1.17. ábra).
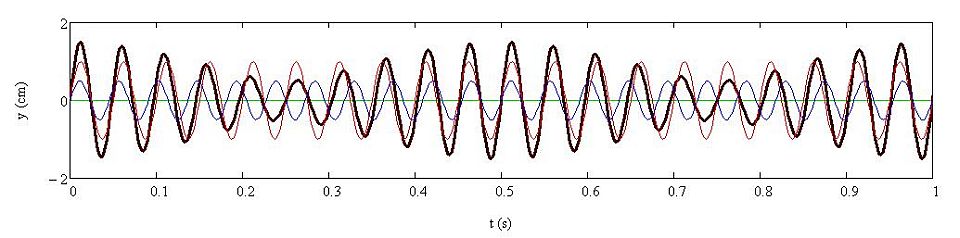
1.1.17. ábra Két egyirányú, kissé eltérő frekvenciájú és különböző amplitúdójú harmonikus rezgés (y1(t) és y2(t)), valamint az eredő rezgés (y(t)) kitérés-idő függvénye. Paraméterek: A1= 1 cm, A2 = 0,5 cm, ν1 = 20 Hz, ν2 = 22 Hz, φ1 = φ2 =0 rad
Magyarázat: Mivel a két rezgés amplitúdója különbözik, ezért az 1.1.5. fejezetben bemutatott azonos frekvenciájú, de különböző amplitúdójú rezgések összeadásához hasonlóan, most sem lesz kioltás, csak gyengítés, ezért az eredő rezgés amplitúdója sosem csökken le zérusra.
Kísérlet : Egy kiskocsit egy vízszintes alumínium sínre helyezünk. A kiskocsira rászerelünk egy rugós kilövőegységet, ami a belehelyezett műanyag golyót a kocsi talapzatára merőlegesen, azaz jelen esetben függőlegesen felfelé lövi ki. A kiskocsit meglökjük, és amikor elér a sín mellett elhelyezett kapcsolóig, az aktiválja a kilövő szerkezetet, és kirepül a golyó.
Megfigyelés:
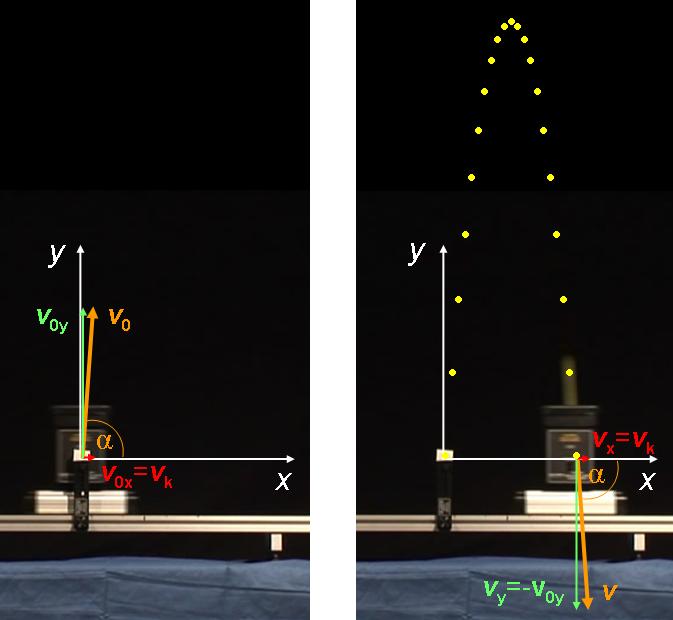
1.1.18. ábra A kocsiról kilőtt műanyag golyó parabola alakú pályán repül, és végül visszaesik az egyenletes sebességgel haladó kocsira. A sárga szimbólumok a golyónak a kilövéstől számítva egyenlő időközönként mért helyzetét jelölik.
Magyarázat: A jelenség matematikai leírásához a koordináta-rendszer origóját rögzítsük a tér azon pontjához, mely egybeesik a kilövő szerkezetben lévő golyó közepével a kilövés pillanatában, azaz t=0-ban (1.1.18. ábra). A koordináta-rendszer x-tengelye mutasson a kocsi mozgásának irányába, az y-tengely pedig függőlegesen felfelé. Az ily módon megválasztott koordináta-rendszer tehát a jelenség lefolyása alatt végig a teremhez képest nyugalomban van. A kocsin elhelyezett kilövőszerkezet a golyót függőlegesen felfelé lövi ki v 0y kezdősebességgel. A golyó v 0 sebességvektora ebben a koordináta-rendszerben mégsem függőlegesen felfelé mutat, hanem kissé ferdén felfelé előre. Ennek oka, hogy a kilövő szerkezet a kocsival együtt mozog egyenletes v k sebességgel balról jobbra, így a golyónak van egy, a kocsi sebességével megegyező vízszintes irányú v ox = v k sebességkomponense is. Ezért a golyó mozgása egy ferde hajításnak felel meg.
Egy korábbi kísérletnél már láttuk, hogy a vízszintes sínen ellökött kocsi egyenletes sebességgel mozog (elhanyagolható súrlódás esetén). Mivel a golyó visszaesik a kocsira, ez azt jelenti, hogy a vízszintes sebességkomponense nem változott a repülés során. A golyó pályájának tetőpontjától lefelé nézve láthatjuk, hogy egyenlő időközönként a golyó egyre nagyobb utakat tesz meg, hasonlóan a szabadeséshez. Ha pontosan megmérnénk a golyónak a síntől mért magasságát, akkor valóban azt kapnánk, hogy adott időpillanatokban éppen olyan magasan van, mint ahol egy szabadon eső test is lenne. Így tehát azt kaptuk, hogy a ferde hajítás felbontható egy vízszintes irányú egyenes vonalú egyenletes mozgásra és egy függőleges irányú egyenletesen változó mozgásra, ahol a testnek a gyorsulása egyenlő a nehézségi gyorsulással: x(t) = v 0 cos(α)t és y(t) = v 0 sin(α)t-gt 2 /2. Ha e két egyenletből kiszámoljuk a test pályáját, akkor valóban egy parabolát kapunk, és adódik, hogy a golyónak a kocsiba való visszaesésekor a sebessége megegyezik az indulási sebességével, azaz v=v0.
Kísérlet: Egy animáció segítségével vizsgáljuk meg, hogy egy egyenletes körmozgást végző test egyenlő időközök alatt mekkora ívhosszakat fut be! A körmozgás periódusideje 30 s. 5 másodpercenként a körpálya középpontját a testtel összekötő piros vonal jelenik meg. Egy másik animáción pedig figyeljük meg, hogy a mozgás során milyen irányba mutat a test sebességvektora (zöld nyíl) és gyorsulásvektora (piros nyíl)!
Megfigyelés:
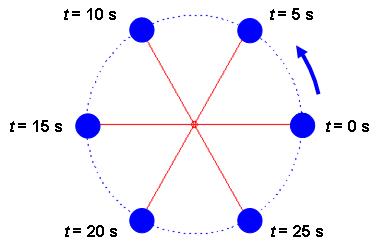
1.1.19. ábra A körpályán mozgó test 5 másodpercenként, azaz egyenlő időtartamok alatt egyenlő íveket és középponti szögeket fut be
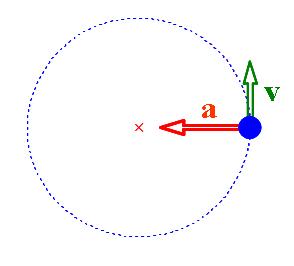
1.1.20. ábra A körpályán mozgó test sebességvektora mindig a pálya érintőjének, míg a gyorsulásvektora a kör középpontjának irányába mutat
Magyarázat: Egyenletes körmozgást végző test esetén bármekkora Δt időtartam esetén is érvényes, hogy azonos Δt időtartamok alatt azonos Δs ívhosszakat fut be és a Δφ szögelfordulás is azonos. Ebből következően Δs/Δt= állandó és Δφ/Δt= állandó. Az első összefüggéssel definiáljuk a körmozgás kerületi sebességének nagyságát: v = Δs/Δt, míg a második összefüggéssel a szögsebességet: ω= Δφ/Δt.
A körmozgás periódusideje alatt azt a T időtartamot értjük, amely alatt a test egy teljes kört tesz meg, azaz ekkor Δt = T és Δs=2Rπ, ahol R a körpálya sugara. Ebből következően a kerületi sebesség nagysága: v = 2Rπ/T . A szögsebességre vonatkozóan pedig mivel Δφ = 2π, így ω = 2π/T. A két összefüggésből a kerületi sebesség és a szögsebesség közötti kapcsolatra kapjuk, hogy v = Rω.
A kerületi sebesség irányának meghatározásához tekintsük azt az esetet, amikor egy adott t időpontban a test a körpálya P pontjában van, majd Δt idő múlva pedig a P' pontban (1.1.21. ábra). A test Δr = r(t+Δt)-r(t) elmozdulás vektorának iránya a vektorok kivonására tanultak szerint az ábrán látható, mely egyben a PP' vektor iránya is. Ez utóbbi a hosszát tekintve pedig nem más, mint a kör egy húrja. A Δr/Δt vektor iránya megegyezik a Δr vektor irányával. Mivel a sebességvektor a helyvektor idő szerinti differenciálhányadosa, így ha a Δt időtartamot egyre csökkentjük, azaz Δt tart zérushoz, akkor a Δr/Δt vektor határértékben éppen a sebességvektort adja, és az iránya pedig az érintő irányával egyezik meg.
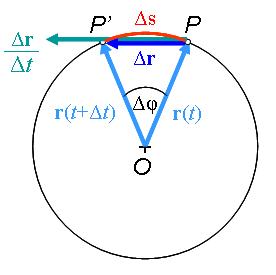
1.1.21. ábra A körpályán mozgó test sebességvektorának meghatározása
Bár a test sebességvektorának a nagysága nem változik a mozgás során, azonban az iránya igen. Mivel definíció szerint a gyorsulásvektor a sebességvektor idő szerinti első differenciálhányadosa, ezért a testnek az egyenletes körmozgás során a gyorsulásvektora nem zérus. A gyorsulásvektor irányának meghatározásához egy adott t időpillanatban legyen a test a pálya P pontjában, majd Δt idővel később a P' pontban (1.1.22. ábra). Az APB szög egyenlő Δφ-vel, mert a v(t) vektor a P, míg a v(t+Δt) vektor a P' ponthoz tartozó érintővel párhuzamos. A sebesség nagysága nem változik, azaz a v(t) és a v(t+Δt) vektorok hossza ugyanakkora, ezért a PAB háromszög egy egyenlő szárú háromszög. Ebből következik, hogy az A csúcsnál lévő szög 90°-Δφ/2, azaz a Δv vektor és így a Δv/Δt vektor is ekkora szöget zár be a P- beli érintővel. Ha a Δt és ezzel együtt a Δφ zérushoz tart, akkor határesetben a Δv/Δt vektor a gyorsulásvektort adja, mely merőleges lesz a P-beli érintőre, vagyis a kör középpontja felé mutat.
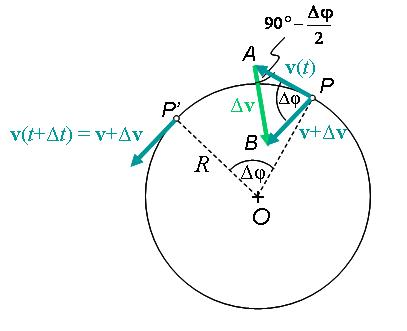
1.1.22. ábra A körpályán mozgó test gyorsulásvektorának meghatározása
Ami a gyorsulás nagyságát illeti, az APB háromszög AB = Δv oldala kicsiny Δφ esetén Δv=vΔφ=vΔs/R, azaz Δv/Δt=(v/R)(Δs/Δt), ahol R a körpálya sugara. Ha Δt tart zérushoz, akkor kapjuk, hogy a gyorsulás nagysága: a=v2/R. Ez az állandó nagyságú, de folytonosan változó irányú, mindig a kör középpontja felé mutató gyorsulás az ún. centripetális gyorsulás.
Kísérlet: Vizsgáljuk meg a körmozgás és a harmonikus rezgőmozgás kapcsolatát egy animácó segítségével! Az egyik test egy egyenletes körmozgást, míg a másik test harmonikus rezgőmozgást végez ugyanabban a síkban. A körmozgás periódusideje megegyezik a rezgés periódusidejével, és a körpálya sugara egyenlő a rezgés amplitúdójával.
Megfigyelés:
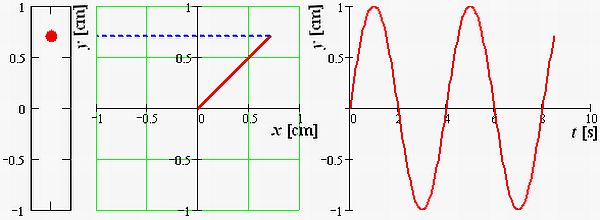
1.1.23. ábra A körmozgást végző test függőleges tengely menti kitérése (helyvektorának a függőleges tengelyre eső vetülete) mindig megegyezik a harmonikus rezgőmozgást végző test kitérésével
Magyarázat: A körmozgást végző test helyvektorának a függőleges tengelyre eső vetülete y(t) = r sin(Ωt), ahol Ω a körmozgás szögsebessége. A harmonikus rezgőmozgást végző test kitérés-idő függvénye y(t) = Asin(ωt), ahol ω a rezgés körfrekvenciája. Ha Ω=ω és A = r, akkor a körmozgást végző test y koordinátája ugyanúgy változik időben, mint a harmonikus rezgőmozgást végző testé.
Kísérlet: Vizsgáljuk meg animáció segítségével két egymásra merőleges, azonos frekvenciájú és azonos amplitúdójú harmonikus rezgés összegét, ha a rezgések közötti fáziskülönbség δ= 0 rad!
Megfigyelés: Az eredő rezgést végző pont pályája egy egyenes, azaz lineáris rezgés (más néven lineárisan poláros rezgés) jön létre (1.1.24. ábra). Az egyenes 45 fokban dől az x-tengelyhez képest, azaz a meredeksége 1.
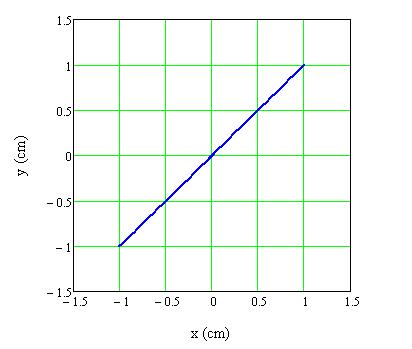
1.1.24. ábra Két egymásra merőleges, azonos frekvenciájú és azonos amplitúdójú harmonikus rezgés összege, ha a rezgések közötti fáziskülönbség δ= 0 rad
Magyarázat: A két rezgés kitérés-idő függvénye x(t) = A x sin(ωt) és y(t) = A y sin(ωt+δ).
Az eredő rezgést végző pont pályájának egyenlete: x 2 /A x 2 +y 2 /A y 2 -2xycosδ/A x A y =sin 2 δ.
Mivel ebben az esetben Ax=Ay és δ= 0 rad, így a pálya egyenlete: y = x.
Kísérlet: Vizsgáljuk meg animáció segítségével két egymásra merőleges, azonos frekvenciájú és azonos amplitúdójú harmonikus rezgés összegét, ha a rezgések közötti fáziskülönbség δ=π/4 rad!
Megfigyelés: Az eredő rezgést végző pont pályája ellipszis alakú, azaz elliptikus rezgés (elliptikusan poláros rezgés) alakul ki (1.1.25. ábra). A rezgő pont az óramutató járásával megegyező irányban halad végig a pályáján.
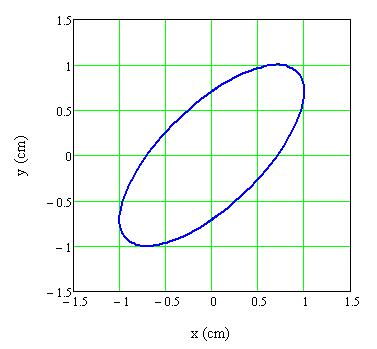
1.1.25. ábra Két egymásra merőleges, azonos frekvenciájú és azonos amplitúdójú harmonikus rezgés összege, ha a rezgések közötti fáziskülönbség δ= π/4 rad
Magyarázat: A fenti paraméterekkel kiszámítható, hogy ebben az esetben a pálya egyenlete egy ellipszis, amely az x-tengellyel 45 fokot zár be. Bár a szimuláción is jól látszik, hogy a rezgő pont miért az óramutató járásával megegyező irányban halad végig a pályáján, de nézzük meg, hogy az x(t) és az y(t) kitérés-idő függvényekből ez hogyan adódik. Jelen esetben x(t) = A x sin(ωt) és y(t) = A y sin(ωt+π/4). Vegyük a t=0 időpontot, ekkor x(0)=0 és y(0) pedig pozitív értékű, azaz az eredő rezgést végző pont az y-tengelyen, az x-tengely felett van. Egy kicsiny idővel később az x(t) értéke zérusról pozitív értékre változik, míg az y(t) értéke tovább nő, azaz a rezgő pont valóban az óramutató járásával megegyező irányban indul el az ellipszis alakú pálya mentén.
Kísérlet: Vizsgáljuk meg animáció segítségével két egymásra merőleges, azonos frekvenciájú és azonos amplitúdójú harmonikus rezgés összegét, ha a rezgések közötti fáziskülönbség δ=π/2 rad!
Megfigyelés: Az eredő rezgést végző pont pályája kör alakú, azaz cirkuláris rezgés (körben poláros rezgés) jön létre (1.1.26. ábra). A rezgő pont az óramutató járásával megegyező irányban halad végig a pályáján.
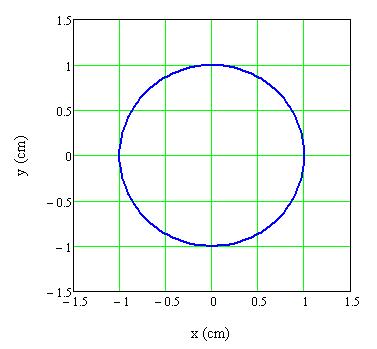
1.1.26. ábra Két egymásra merőleges, azonos frekvenciájú és azonos amplitúdójú harmonikus rezgés összege, ha a rezgések közötti fáziskülönbség δ= π/2 rad
Magyarázat: A fenti paraméterekkel kapjuk, hogy ebben az esetben a pálya egyenlete: x 2 +y 2 =1, azaz egy 1 cm sugarú körpálya.
Kísérlet: Vizsgáljuk meg animáció segítségével két egymásra merőleges, azonos frekvenciájú és azonos amplitúdójú harmonikus rezgés összegét, ha a rezgések közötti fáziskülönbség δ=3π/4 rad!
Megfigyelés: Az eredő rezgést végző pont pályája ellipszis alakú, azaz elliptikus rezgés keletkezik (1.1.27. ábra). A rezgő pont az óramutató járásával megegyező irányban halad végig a pályáján. Ebben az esetben az ellipszis nagytengelye az x-tengellyel 135 fokot zár be.
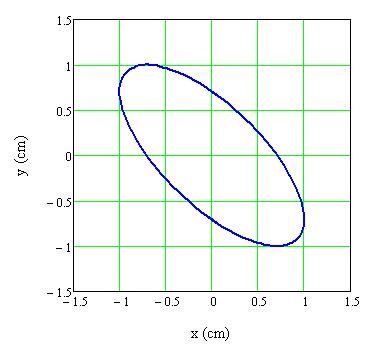
1.1.27. ábra Két egymásra merőleges, azonos frekvenciájú és azonos amplitúdójú harmonikus rezgés összege, ha a rezgések közötti fáziskülönbség δ= 3π/4 rad
Magyarázat: A fenti paraméterekkel kapjuk, hogy ebben az esetben a pálya egyenlete egy ellipszis, amely az x-tengellyel 135 fokot zár be.
Kísérlet: Vizsgáljuk meg animáció segítségével két egymásra merőleges, azonos frekvenciájú és azonos amplitúdójú harmonikus rezgés összegét, ha a rezgések közötti fáziskülönbség δ = π rad!
Megfigyelés: Az eredő rezgést végző pont pályája egyenes, azaz lineáris rezgés alakul ki. Az egyenes meredeksége -1 (1.1.28. ábra).
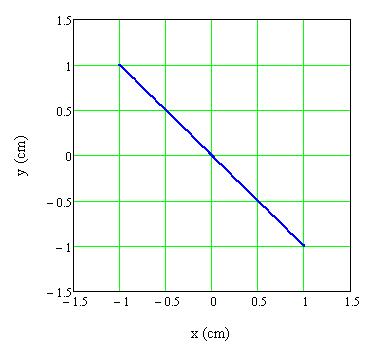
1.1.28. ábra Két egymásra merőleges, azonos frekvenciájú és azonos amplitúdójú harmonikus rezgés összege, ha a rezgések közötti fáziskülönbség δ= π rad
Magyarázat: A fenti paraméterekkel kapjuk, hogy ebben az esetben a pálya egyenlete: y=-x.
Kísérlet: Vizsgáljuk meg animáció segítségével két egymásra merőleges, különböző frekvenciájú (νy= 2νx) és azonos amplitúdójú harmonikus rezgés összegét, ha a rezgések közötti fáziskülönbség δ= 0 rad!
Megfigyelés: Az eredő rezgést végző pont pályájának alakja egy fektetett nyolcasra emlékeztet (1.1.29. ábra).
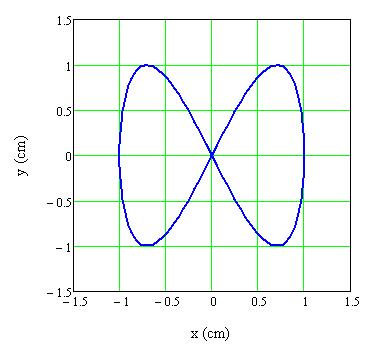
1.1.29. ábra Két egymásra merőleges, különböző frekvenciájú (νy= 2νx) és azonos amplitúdójú harmonikus rezgés összege, ha a rezgések közötti fáziskülönbség δ= 0 rad
Magyarázat: A két rezgés egyenletéből kiszámolható a fent látható pálya. Amikor a két rezgés frekvenciája nem egyezik meg, akkor bonyolultabb pályák alakulnak ki, az ún. Lissajous-görbék. Ha a két rezgés frekvenciájának hányadosa racionális szám, akkor a pálya zárt görbe, mint jelen esetben is látható.
Kísérlet:Egy kiskocsit egy egyenes és vízszintes alumínium sínen meglökünk. A kocsi fém kerekei és a sín között fellépő súrlódás gyakorlatilag elhanyagolható. A mozgás során a kocsi helyzetét és sebességét vektorszkóp segítségével határozzuk meg. A vektorszkóp tornyát a sín végéhez tesszük, míg a gombot a kiskocsira helyezzük.
Megfigyelés: A kocsi egészen addig nyugalomban volt, míg meg nem löktük. A lökés után egyenletes sebességgel haladt végig a sínen.
Magyarázat: A tehetetlenség törvénye szerint van olyan vonatkoztatási rendszer, az ún. inerciarendszer, melyben minden test mindaddig megtartja mozgásállapotát, azaz nyugalmi állapotát, vagy egyenes vonalú egyenletes mozgását, amíg más testekkel való kölcsönhatása annak megváltoztatására nem kényszeríti.
A kísérlet folyamán a Földnek és a sínnek a kocsira gyakorolt hatása egymást kompenzálja, így a kocsi mozgásállapotát nem befolyásolják. A kocsi egészen addig nyugalmi állapotban volt a sínhez rögzített vonatkoztatási rendszerben, amíg meg nem löktük, azaz nem lépett fel kölcsönhatás a kocsi és a kezünk között. A lökés időtartama alatt a kocsi sebessége folyamatosan nőtt. Miután magára hagytuk a kocsit, attól kezdve ismét csak a Föld és sín hatott a kocsira, mely hatások viszont egymást kompenzálják. Így a továbbiakban a kocsi a mozgásállapotát ismét őrzi, azaz a lökés során elért sebességgel haladt végig a sínen.
A kísérleti eredményéből, azaz abból, hogy csak akkor változott a kocsi mozgásállapota, amikor a kezünkkel hatottunk rá, arra következtethetünk, hogy a sínhez rögzített vonatkoztatási rendszer inerciarendszer.
Kísérlet:Egy kiskocsit egy egyenes és vízszintes alumínium sínre helyezünk. Az 520 g tömegű kiskocsihoz egy fonalat kötünk, melyet egy a sín végén lévő csigán átvetünk. A kísérlet első felében a fonal másik végére 12,5g, 25g illetve 50g tömegű nehezéket erősítünk. A kísérlet második felében a nehezék tömege mindig 50g, a kocsira viszont előbb 300g, majd 600g terhet teszünk. A mozgás során a kocsi sebességét és gyorsulását vektorszkóp segítségével határozzuk meg. A vektorszkóp tornyát a sínnek a csigával átellenes végéhez tesszük, míg a gombot a kocsira helyezzük.
Megfigyelés: A kísérlet első felében, amikor a kocsit különböző tömegű nehezékekkel gyorsítjuk, azt látjuk, hogy kétszer nagyobb tömegű nehezék nagyjából kétszer akkora gyorsulást okoz (1.2.1. ábra). Ha jobban megnézzük a grafikonokat, akkor észrevehetjük, hogy nem pont kétszer akkorák a gyorsulás értékei. A legkisebb tömegű nehezék esetében különösen feltűnő az eltérés, melynek okára a magyarázatban később kitérünk.
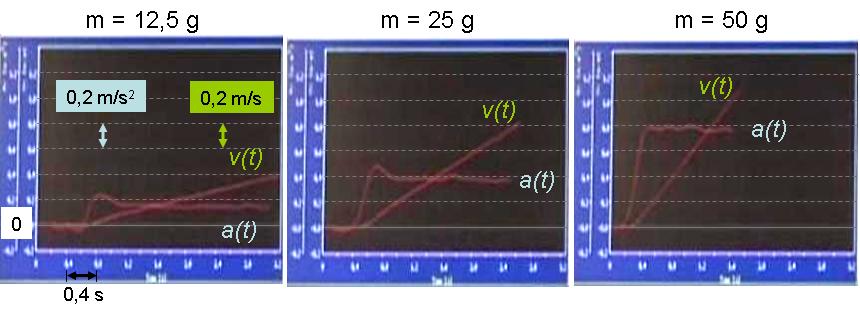
1.2.1. ábra A kocsi sebessége és gyorsulása az idő függvényében különböző nehezékekkel való gyorsítás esetén
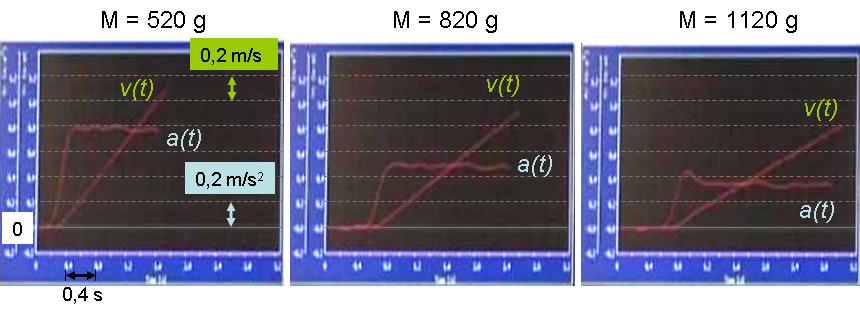
A kísérlet második felében, amikor a gyorsító tömeg ugyanakkora, viszont a kocsi tömege egyre nagyobb, azt látjuk, hogy a kocsi gyorsulása egyre kisebb (1.2.2. ábra). Miközben a kocsi össztömege a ráhelyezett teherrel együtt a 8/5-ére illetve 11/5-re nőtt a kezdeti értékhez képest, a gyorsulás értéke nagyjából 5/8-ára illetve 5/11-ére csökkent.
Magyarázat: Ezzel a kísérlettel az F=ma összefüggés érvényességét demonstrálhatjuk. Arra fel kell hívni a figyelmet, hogy Newton II. axiómája egy adott testre ható erő és a test gyorsulása közötti kapcsolatra vonatkozik. Ha csak a kocsi mozgására koncentrálunk, és figyelembe vesszük, hogy a kocsira ható nehézségi erő és a sín által a kocsira gyakorolt nyomóerő egymás hatását kompenzálja, akkor a kocsi mozgását, gyorsulását a fonálerő okozza, feltéve, ha a súrlódástól eltekintünk. Ekkor a kocsit gyorsító fonálerő F=mMg/(m+M), azaz Newton II. axiómája szerint a kocsi gyorsulása: a=F/M=mg/(m+M), ahol m a nehezék és M a kocsi tömege. Ha m << M, akkor a nevezőben a nehezék tömege elhagyható a kocsi tömege mellől, és így a kocsit gyorsító fonálerő nagysága mg, a gyorsulás pedig a=mg/M. Eszerint, ha a nehezék tömege kétszeresére változik, akkor a kocsi gyorsulásának is kétszeresére kell változni. Nagyjából ezt is tapasztaltuk a kísérlet során, de éppen a legkisebb tömegű nehezéknél, ahol egyébként a jobb egyezést várnánk, látható leginkább az eltérés.
Ha a gyorsulásra vonatkozó képlet nevezőjében nem hanyagoljuk el a nehezék tömegét, akkor a gyorsulásra az m= 50, 25 és 12,5 g tömegű nehezékeknél 0,86, 0,45 és 0,23 m/s2 adódik, azaz a leolvasás pontosságán belül teljesülni kellett volna, hogy a gyorsulás értéke megkétszereződik. Ezzel szemben a mért értékek 0,78, 0,36 és 0,14 m/s2, melyek egymásnak nem teljesen a kétszeresei, és kisebbek a képletből adódónál. Ez azt jelenti, hogy a súrlódást mégiscsak figyelembe kell vennünk a jelenség pontos leírásához. Ekkor a gyorsulás értékére vonatkozó képlet az alábbi alakú lesz: a= (m-μM)g/(m+M), ahol μ a súrlódási együttható. Jelen esetben a mért gyorsulásokból kiszámolva μ=0,0095 adódik. Vegyük észre, hogy súrlódási erő nemcsak a kerekek és a sín között, hanem a kocsitengely csapágyazásánál is fellép. Így a kísérlet során e két súrlódási erő együttes hatást mértük meg. A képletből látható, hogy mennél kisebb a nehezék tömege, annál jelentősebb a súrlódás hatása a gyorsulás értékére, ahogy ez a fenti grafikonokon is látszik.
Ezután vizsgáljuk meg azt az esetet, amikor a gyorsító erő állandó, és a gyorsítandó tömeg változik. Induljunk ki megint a legegyszerűbb összefüggésből, azaz a=mg/M. Eszerint, ha a kocsi tömege 520 grammról 820 illetve 1120 grammra növekszik, a kocsi gyorsulásának 5/8-ra illetve 5/11-re kell csökkennie. Az 1.2.2. ábrán nagyjából ilyen mértékű a gyorsulások csökkenése. Ha a gyorsulások mért értékeit nézzük, akkor azok ismét nem egyeznek meg a fenti egyszerű képletből adódó értékekkel, hanem a kísérlet első feléhez hasonlóan, figyelembe kellene venni a súrlódási erőnek a kocsi gyorsulására gyakorolt hatását is.
Kísérlet:Függesszünk fel egy kb. egy méter hosszú fonálra egy fémből vagy műanyagból készült golyót. Fontos, hogy a fonál minél kisebb, a golyó pedig minél nagyobb tömegű legyen. A golyót fogjuk meg és mozdítsuk ki az egyensúlyi helyzetéből úgy, hogy a fonál feszes legyen. Ezután lökjük meg úgy a golyót, hogy vízszintes síkú körmozgást végezzen!
Megfigyelés: Megfelelően mozgásba hozva a golyót, a golyó körpályán mozog, mégpedig úgy, hogy egyenletes körmozgásnak látjuk. A fonál egy 2φ nyílásszögű kúp palástját járja be. Ezt nevezzük kúpingának.
Magyarázat: A kísérlettel a körmozgás dinamikájának megértéséhez kerülhetünk közelebb. A mozgást ebben az esetben is az inerciarendszernek tekintett teremhez viszonyítva, pontosabban szólva egy ehhez képest nyugvó megfigyelő (jelen esetben a nyugvó helyzetben lévő kamera) szempontjából írjuk le. Az 1.1.8. fejezetben már láttuk, hogy az állandó ω szögsebességgel egyenletes körmozgást végző tömegpont gyorsulása az állandó nagyságú és mindig a kör középpontja felé mutató centripetális gyorsulás, azaz acp=-ω2r, ahol r a kör középpontjából a tömegponthoz húzott rádiuszvektor.
Az F=ma dinamikai alapegyenlet szerint az acp gyorsulásnak megfelelő erő, a centripetális erő Fcp=-mω2r, mely nem más, mint a tömegpontra ható összes erő eredője. Ez az állandó nagyságú, és a kör középpontja felé mutató erő mindig merőleges a tömegpont v sebességére, és ily módon a sebességnek csak az iránya változik, a nagysága nem. A centripetális erő nagysága többféle alakban is megadható: Fcp= mv 2 /r illetve Fcp= mrω2, ahol r a körpálya sugara, v a kerületi sebesség, ω pedig a szögsebesség.
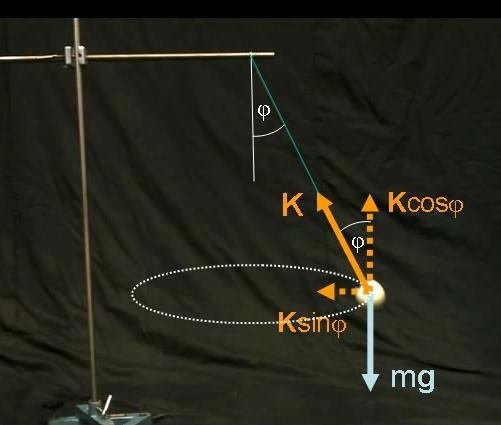
1.2.3. ábra A kúpinga esetében a körmozgáshoz szükséges erőt a kötélerő vízszintes irányú komponense biztosítja
Jelen esetben az m tömegű golyóra két erő hat. Az egyik a saját tömegéből adódó mg nehézségi erő, a másik pedig a fonál által kifejtett K fonálerő. Így a dinamika alapegyenlete a testre vonatkozóan: mg+K=ma. Az mg függőlegesen lefelé mutat, míg a K pedig értelemszerűen a fonál irányában a felfüggesztési pont felé. Bontsuk fel a K fonálerőt egy függőleges (Kcosφ) és egy vízszintes (Ksinφ) irányú komponensre. Mivel a fonál végén lévő test vízszintes síkban mozog, ezért függőleges irányban nincs gyorsulása, tehát az erők eredőjének függőleges irányban zérusnak kell lenni: mg=Kcosφ. Vízszintes irányban csak a Ksinφ erő hat, azaz a dinamika alapegyenletéből adódik, hogy Ksinφ=macp. Ez azt jelenti, hogy a kúpinga esetében a körmozgáshoz szükséges centripetális erő szerepét a tömegpontra ható erők eredője, a fonálerő vízszintes irányú komponense tölti be.
Kísérlet: Egy vízszintes alumínium sínre két azonos tömegű kiskocsit helyezünk, egyiket a sín közepére, a másikat a sín egyik végére. A két kocsit úgy helyezzük el, hogy az egymás felé néző végükön lévő mágnesek ellentétes pólusúak legyenek, azaz ütközéskor vonzzák egymást. A sín szélén lévő kocsit meglökjük, és a kocsik sebességét vektorszkóppal mérjük. A sín szabad végéhez tesszük a vektorszkóp tornyát, a kocsikra pedig egy-egy gombot helyezünk.
Megfigyelés: A sín szélén lévő kocsi a meglökése után egyenletes v1 sebességgel haladt (1.3.1 ábra), majd nekiütközött a nyugalmi állapotban lévő kocsinak. Ekkor a két kocsi összetapadt és a meglökött kocsi ütközés előtti sebességének felével haladtak tovább.
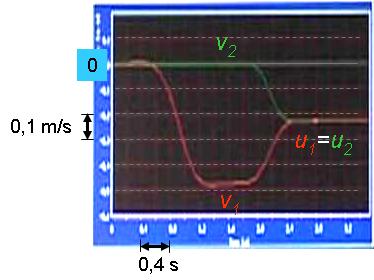
1.3.1. ábra Rugalmatlan ütközéskor a két kocsi összetapad és az ütközés utáni sebességeik megegyeznek
Magyarázat: Jelen esetben a jelenség szempontjából a kocsik mérete elhanyagolható, azaz pontszerűeknek tekinthetők. Így a két kocsira, mint pontrendszerre ható külső erők a Föld nehézségi ereje és a sín nyomóereje (a súrlódási erőt elhanyagoljuk). Ezen erők eredője kocsinként zérus, azaz a pontrendszerre ható külső erők eredője zérus, így érvényes a pontrendszerekre vonatkozó impulzusmegmaradás-tétele. Jelöljük a két kocsi tömegét m 1 -gyel és m 2 -vel. Mivel a kocsik sebességvektora egy egyenesbe esik, ezért a vektoros jelölés helyett használhatunk skalár jelölést azzal a megkötéssel, hogy a sebesség értéke pozitív, ha a vektorszkóp tornyától távolodik a kocsi, és negatív, ha közeledik hozzá. A kocsik ütközés előtti sebessége legyen v1 és v2. Mivel tökéletesen rugalmatlan az ütközés, ez azt jelenti, hogy a két kocsi ütközés után együtt halad. A közös sebességüket jelöljük u-val (u=u 1 =u 2 ). Az impulzusmegmaradás-tétele alapján: u=(m 1 v 1 +m 2 v 2 )/(m 1 +m 2 ). Esetünkben m 1 =m 2 ,v 1 =v és v 2 =0, így a kocsik ütközés utáni sebessége: u=v/2.
Az 1.3.1. ábrán az ütközés előtt a mozgó kocsi sebessége v1= -0,47 m/s. A negatív előjel arra utal, hogy a kocsi a vektorszkóp tornya felé haladt az ütközés előtt. Ütközés után a két kocsi közös sebessége -0,23 m/s, azaz a mérés pontosságán belül (5 %) egyezik az elmélet alapján várt értékkel. A negatív előjel pedig azt mutatja, hogy az ütközés után az összetapadt kocsik a torony felé mozogtak.
Kísérlet: Egy vízszintes alumínium sínre két kiskocsit helyezünk, egyiket a sín közepére, a másikat a sín egyik végére. A két kocsit úgy helyezzük el, hogy az egymás felé néző végükön lévő mágnesek azonos pólusúak legyenek, azaz ütközéskor taszítsák egymást. A sín szélén lévő kocsit meglökjük, és a kocsik pillanatnyi sebességét vektorszkóppal mérjük. A sín szabad végéhez tesszük a vektorszkóp tornyát, a kocsikra pedig egy-egy gombot helyezünk.
Megfigyelés: A sín szélén lévő kocsi a meglökése után egyenletes v1 sebességgel haladt. Miután nekiütközött a nyugalmi állapotban lévő kocsinak, a két kocsi sebességet cserélt, ahogy az 1.3.2. ábrán is látható. Az eddig mozgó kocsi nyugalomba került, a nyugalomban lévő kocsi viszont a másik kocsi sebességével haladt tovább. Lehet látni, hogy a mozgó kocsik sebessége folyamatosan csökken, ami azt mutatja, hogy némi súrlódás fellép a mozgás során.
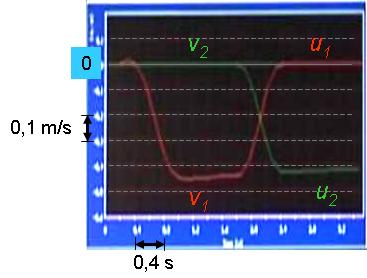
1.3.2. ábra Azonos tömegű kocsik a rugalmas ütközéskor sebességet cserélnek
Magyarázat: A rugalmatlan ütközésnél ismertetett okok miatt itt is érvényes a pontrendszerekre vonatkozó impulzusmegmaradás-tétele. Jelöljük a két kocsi tömegét m 1 -gyel és m 2 -vel. Mivel a kocsik sebességvektora egy egyenesbe esik, ezért a vektoros jelölés helyett használhatunk skalár jelölést azzal a megkötéssel, hogy a sebesség értéke pozitív, ha a vektorszkóp tornyától távolodik a kocsi, és negatív, ha közeledik hozzá. A kocsik ütközés előtti sebessége legyen v1 és v2. Mivel tökéletesen rugalmas az ütközés, ezért a kocsiknak az ütközés előtti mozgási energiájuk összege megegyezik az ütközés utáni mozgási energiájuk összegével. E két törvény alapján az ütközés utáni sebességek: u 1 =((m 1 -m 2 )v 1 +2m 2 v 2 )/(m 1 +m 2 ),u2-re hasonló az összefüggés, csak az 1 és 2 indexeket fel kell cserélni.
Esetünkben m 1 =m 2 és v 2 =0, így az ütközés utáni sebességek: u 1 =v 2 =0 és u 2 =v 1 . Az 1.3.2. ábrán az ütközés előtti pillanatokban a mozgó kocsi sebessége v1= -0,44 m/s, azaz a vektorszkóp tornya felé közeledett, majd az ütközés után megállt (u1=0 m/s). Az ütközésig nyugalomban lévő kocsi sebessége u2=-0,42 m/s lett, azaz a mérés pontosságán belül (5 %) egyezik az elmélet alapján várt értékkel, és ugyanabban az irányban haladt tovább, mint a nekiütköző kocsi.
Vegyük észre, hogy az ütközés nem feltétlenül jelenti azt, hogy fizikailag össze is érnek a kocsik, mert a kocsik szélén lévő mágnesek között fellépő taszító erők közvetítik a kölcsönhatást. Ha a tökéletesen rugalmas ütközést akarjuk vizsgálni, akkor ügyelnünk is kell arra, hogy a kocsik az ütközés folyamán fizikailag ne érjenek össze, mert ez energiaveszteséget okoz (pl. a hanghatás létrejötte is energiát igényel.)
Kísérlet: A kísérlet az előbbihez hasonló, csak az ütközés előtt nyugalomban lévő kocsira 300 g tömegű terhet teszünk.
Megfigyelés: A sín szélén lévő kocsi a meglökése után egyenletes sebességgel haladt a torony felé -0,47 m/s sebességgel (1.3.3. ábra). Miután nekiütközött a nyugalmi állapotban lévő kocsinak, visszapattant róla, és a toronytól 0,09 m/s sebességgel távolodott. A sebessége jelentősen csökkent a mozgás során. A nagyobb tömegű kocsi az ütközés után a torony felé kezdett mozogni -0,35 m/s-os sebességgel, és a sebessége lényegében nem változott.
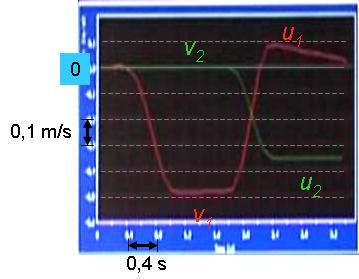
1.3.3. ábra A rugalmas ütközésben résztvevő kocsik sebesség-idő grafikonja. A nagyobb tömegű kocsi az ütközés előtt nyugalomban van
Magyarázat: A fentiek alapján, figyelembe véve, hogy m 1 =520 g, m 2 =820 g, és az ütközés előtti mért sebességek v1=-0,47 m/s és v 2 =0 m/s, az összefüggésekből az ütközés utáni sebességekre u1= 0,11 m/s, u 2 = -0,37 m/s adódik. Megállapíthatjuk, hogy a mérés pontosságán belül (5 %) egyeznek a mért értékekkel.
Az a tapasztalat, hogy a torony felé közeledő kocsi sebessége alig csökken, míg a toronytól távolodó kocsi sebessége viszont jobban csökken, arra enged következetni, hogy a sín nem volt teljesen vízszintes. Így a torony felé haladva a nehézségi erő sín irányú komponense a súrlódási erő hatását lényegében kompenzálja, míg ellenkező irányban hozzáadódik a súrlódási erőhöz.
Kísérlet: A kísérlet az előbbihez hasonló, csak az ütközés előtt nyugalomban lévő kocsira 600 g tömegű terhet tettünk.
Megfigyelés: Az 1.3.4. ábrán látható sebesség-idő grafikonokat kaptuk. Az ütközés előtt v1=-0,40 m/s sebességgel mozgó kocsi az előbbi kísérlethez hasonlóan, visszapattant a nyugalomban lévő kocsiról, és u1= 0,13 m/s sebességgel távolodni kezdett a toronytól. A korábban nyugalomban lévő kocsi viszont elindult a torony felé u2= -0,25 m/s sebességgel.
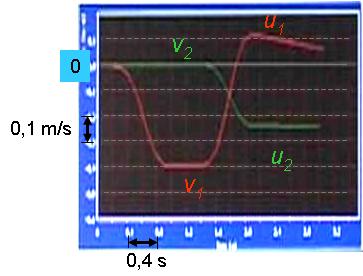
1.3.4. ábra A rugalmas ütközésben résztvevő kocsik sebesség-idő grafikonja. A nagyobb tömegű kocsi az ütközés előtt nyugalomban van
Magyarázat: Az elmélet alapján, felhasználva az ütközés előtti mért sebességeket, az ütközés utáni sebességekre u1=0,15 m/s és u2=-0,25 m/s értékeket kapjuk, azaz a mérés pontosságán belül egyeznek a mért értékekkel.
Kísérlet: A kísérlet az előbbihez hasonló, csak ebben az esetben a sínhez rögzített akadálynak (végtelen nagy tömegnek) ütközik a kocsi.
Megfigyelés: A kocsi nekiütközve az akadálynak, arról visszapattant. Az ütközés utáni sebessége (u1=0,23 m/s) egy kicsivel kisebb az ütközés előtti sebességénél (v1= -0,27 m/s).
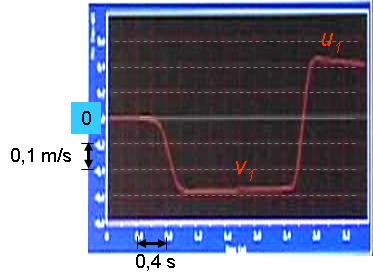
1.3.5. ábra A kocsi sebesség-idő grafikonja, amikor végtelen nagy tömeggel rugalmasan ütközött
Magyarázat: A fejezet elején megadott képletek alapján u1=-v1. Esetünkben némileg kisebb az ütközés utáni sebesség nagysága az ütközés nem tökéletesen rugalmas volta miatt.
Kísérlet: A kísérlet a korábbi ütközési kísérletekhez hasonló. Egyik kocsi nyugalomban van, a másik kocsira 300 g tömegű terhet teszünk, és meglökjük.
Megfigyelés: Az ütközés előtt mozgó kocsi sebessége v1=-0,44 m/s-ról lecsökken u1= -0,10 m/s-ra az ütközés hatására, de továbbra is a torony felé halad (1.3.6. ábra). Az ütközés előtt nyugalomban lévő kocsi sebessége u2= -0,52 m/s-re változik, azaz nagyobb lett az ütközés előtt mozgó kocsi sebességénél.
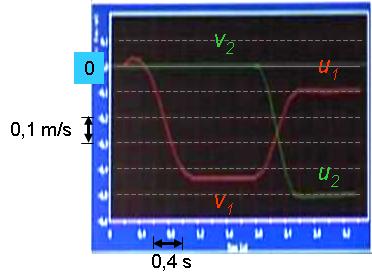
1.3.6. ábra A rugalmas ütközésben résztvevő kocsik sebesség-idő grafikonja. A kisebb tömegű kocsi az ütközés előtt nyugalomban van.
Magyarázat: Az elmélet alapján, felhasználva az ütközés előtti mért sebességeket, u1=-0,10 m/s és u2=-0,54 m/s értékeket kapjuk az ütközés utáni sebességekre, azaz a mérés pontosságán belül egyeznek az ütközés utáni sebességek mért értékeivel.
Kísérlet: A kísérlet az előbbi ütközési kísérlethez hasonló. Az egyik kocsi nyugalomban van, a másik kocsira 600 g tömegű terhet teszünk és meglökjük.
Megfigyelés: Az ütközés előtt mozgó kocsi sebessége v1=-0,40 m/s-ról u1=-0,16 m/s-ra csökkent az ütközés hatására, de továbbra is a torony felé haladt (1.3.7. ábra). A nyugalomban lévő kocsi sebessége u2=-0,52 m/s-ra nőtt, ami nagyobb az ütközés előtt mozgó kocsi sebességénél.
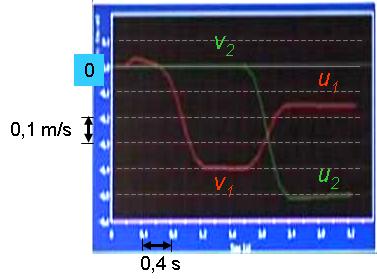
1.3.7. ábra A rugalmas ütközésben résztvevő kocsik sebesség-idő grafikonja. A kisebb tömegű kocsi az ütközés előtt nyugalomban van.
Magyarázat: Az elmélet alapján, felhasználva az ütközés előtti mért sebességeket, u1=-0,15 m/s és u2=-0,55 m/s értékeket kapjuk, azaz a mérés pontosságán belül egyeznek az ütközés utáni sebességek mért értékeivel.
Az impulzusmomentum megmaradásával kapcsolatban a következőkben több kísérletet is bemutatunk, melyekben közös, hogy a kísérletező személy egy forgózsámolyon ül. A forgózsámoly (1.3.8. ábra) egy olyan szék, ami csapágyazott úgy, hogy a függőleges tengely körül nagyon kismértékű súrlódással tud forogni.

1.3.8. ábra A kísérletekhez használt forgózsámoly
Kísérlet: A kísérletező személy a forgózsámolyra ül, és a kezébe súlyzókat adunk. A kísérletező ezután forgásba hozza magát úgy, hogy a lábával a padlótól ellöki magát, miközben a kezében lévő súlyzókat kinyújtott karral tartja. Forgás közben a súlyzókat közelebb húzza magához az 1.3.9. ábra szerint, majd újra kinyújtva a kezét eltávolítja a súlyzókat (1.3.10. ábra). Ezt a műveletsort néhányszor megismétli.

1.3.9. ábra A kísérletező személy a karját behúzva a súlyzókat közelíti a forgástengelyhez, ezzel megnöveli a tengelykörüli forgásának szögsebességét
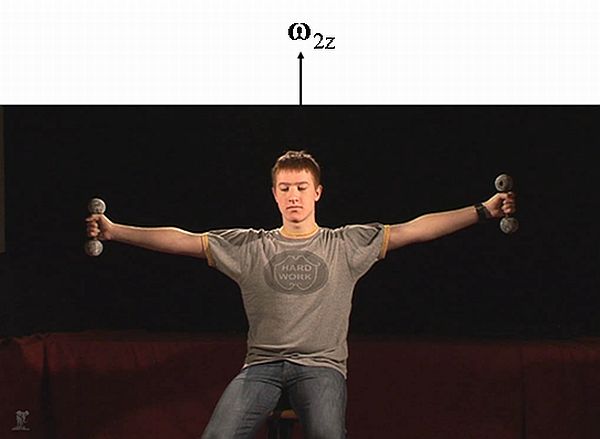
1.3.10. ábra A kísérletező személy a karját kinyújtva a súlyzókat távolítja a forgástengelytől, ezzel lecsökkentve a tengelykörüli forgásának szögsebességét
Megfigyelés: A forgózsámolyon ülő, kezében súlyzókat tartó személy a forgásának szögsebességét változtatni tudja a súlyzóknak a forgástengelytől mért távolságának változtatásával. Ha behúzza a kezét, és így a súlyzók közelebb kerülnek a forgástengelyhez, akkor megnő a forgás szögsebessége. Ha pedig ezután újra kinyújtja a kezét a súlyzókkal, akkor ismét lassul a forgás.
Magyarázat: A pontrendszerekre vonatkozó impulzusmomentum-tétele kimondja, hogy a rendszer teljes impulzusmomentumának (N) időszerinti deriváltja egyenlő a rendszerre ható külső erők forgatónyomatékainak összegével (M), azaz dN/dt = M.
Amikor a kísérletező személy forgásba hozza magát, ezzel a forgózsámolyból, a kísérletező személyből és a súlyzókból álló rendszernek lesz egy a zsámoly forgástengelyére (z-tengelyre) vonatkozó impulzusmomentuma. Mivel a külső erők forgatónyomatéka erre a tengelyre nézve zérus (Mz=0), ezért a fenti tételből következik, hogy a rendszer impulzusmomentumának z irányúkomponense, Nz időben állandó. Nz felírható az Nz=Θωz alakban, ahol Θ a rendszernek a z-tengelyre vonatkozó tehetetlenségi nyomatéka. A fentiek szerint tehát a Θωz szorzatnak állandónak kell lenni.
Amikor a kísérletező személy közelebb húzza magához a kezében lévő súlyzókat, a rendszer Θ tehetetlenségi nyomatékát lecsökkenti. Szükségképpen a fentiek miatt a forgás ωz szögsebességének nőnie kell. Ezért látjuk, hogy távol tartott súlyzókkal a rendszer kisebb szögsebességgel (ω2z), közel tartott súlyzókkal pedig nagyobb szögsebességgel (ω1z) forog, azaz valóban Θ1ω1z=Θ2ω2z.
Kísérlet:A kísérletező személy egy forgózsámolyra ül, és a kezébe adunk egy speciális bicikli abroncsot, melynek a tengelye függőleges irányba mutat. Az abroncs annyiban speciális, hogy az abroncs külső keretéhez előzőleg egy ólomkarikát erősítettünk azért, hogy megnöveljük a tengelyére vonatkozó tehetetlenségi nyomatékát. A kísérletező személy forgásba hozza a kezében tartott, jól csapágyazott abroncsot, majd maga előtt a forgó abroncs tengelyének állását előbb 90 fokkal, majd még további 90 fokkal elfordítja. Ezután többször megismétli az utóbbi mozdulatokat.
Megfigyelés: Amint a kísérletező személy elkezdte forgatni az abroncsot az óramutató járásával ellentétes irányban egy függőleges tengely körül, ő maga is el kezdett forogni a forgózsámolyon ülve, de ellenkező irányban, azaz az óramutató járásával megegyező irányban. Mennél nagyobb sebességgel forgatta meg az abroncsot, annál gyorsabban forgott a zsámolyon ő maga is (1.3.11. ábra).
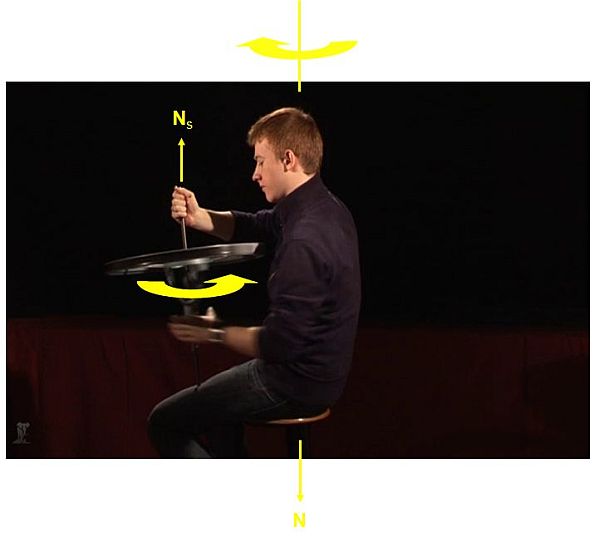
1.3.11. ábra
Amikor a forgó abroncs tengelyét 90 fokkal elfordította, az abroncs forgott tovább, a kísérletező személy forgása viszont megállt. Ha még tovább forgatatta az abroncs tengelyét 90 fokkal, akkor újra el kezdett forogni a kísérletező személy is, de ekkor az óramutató járásával ellentétes irányban (1.3.12. ábra).
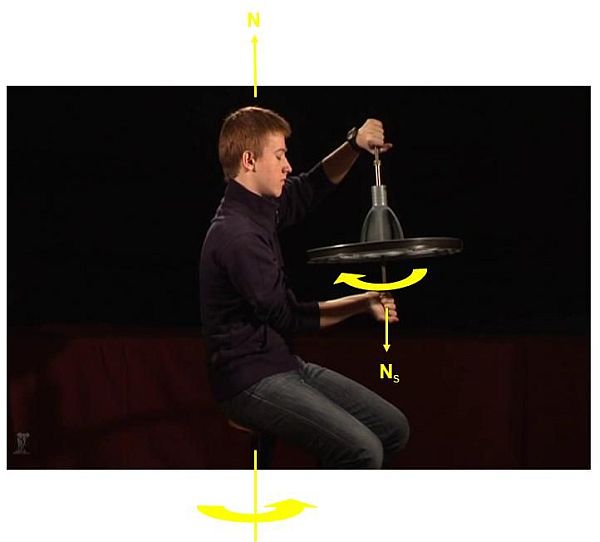
1.3.12. ábra
Magyarázat: Kezdetben nem forog sem az abroncs, sem a kísérletező. Ezért az abroncs, a kísérletező személy és a zsámoly alkotta mechanikai rendszernek a z-tengelyre (a zsámoly forgástengelyén átmenő tengelyre) vonatkozó impulzusmomentuma zérus. Mivel a külső erőknek a z-tengelyre vonatkozó forgatónyomatéka zérus, ezért a rendszer z-tengelyre vonatkozó impulzusmomentumának meg kell maradni az előző kísérletben leírtak miatt, azaz a kísérlet folyamán végig zérusnak kell lennie.
Amikor a kísérletező személy az óramutató járásával ellentétes irányban forgásba hozza az abroncsot, az abroncsnak a saját tengelyére vonatkozó (saját) impulzusmomentum vektorának (N S ) nagysága már nem zérus, és a vektor függőlegesen felfelé mutat. Azért, hogy az abroncs-kísérletező-zsámoly alkotta rendszer eredő impulzusmomentum vektora továbbra is zérus maradjon, elkezd forogni a kísérletező is a zsámollyal és az abronccsal együtt az óramutató járásával egyező irányban. Ez a forgás egy lefelé mutató impulzusmomentum vektort (N) eredményez. Méghozzá éppen olyan szögsebességgel forognak, hogy az eredő impulzusmomentum vektor továbbra is zérus maradjon. Vegyük észre, hogy az N vektor tartalmazza az abroncs z-tengely körüli forgásból származó pályaimpulzusmomentumot.
Abban az esetben, ha a kísérletező személy az abroncsot a kezdeti pozícióhoz képest 180 fokkal elfordítja, azzal az abroncs forgásából származó impulzusmomentum vektorát is elfordítja ugyanekkora szöggel (1.3.12. ábra). Mégpedig az impulzusmomentum vektor változása a nagyságát tekintve 2NS, mivel NS-ről -NS-re változott. Ezért a teljes rendszer (kivéve az abroncs saját tengely körüli forgását) impulzusmomentum vektorának is fordulnia kell. Ezért forog az előzőhöz képest ellentétes irányban a zsámoly.
Amikor 90 fokkal forgatta el a kísérletező a forgó abroncs tengelyét, akkor az abroncs impulzusmomentum vektorának z-irányú komponense zérussá vált. Ezért meg kellett állnia a kísérletező forgásának is, mert csak így teljesülhet, hogy a rendszer z-irányú impulzusmonetum vektora zérus maradjon.
Kísérlet: A kísérletező személy a forgózsámolyra ül. Kezébe adjuk az előbbi kísérletben is használt abroncsot, amit előzőleg kézzel felpörgetünk. A felpörgetést először az óramutató járásával megegyező irányban, majd azzal ellentétesen végezzük el. A kísérlet második részében egy kis villanymotor segítségével a kézi pörgetésnél elért sebességnél jóval nagyobb sebességre pörgetjük fel az abroncsot. A filmen sárga nyíl jelzi a kerék forgási irányát. A kísérletező személy a forgó abroncs tengelyét elforgatja különböző mértékben maga előtt.
Megfigyelés: A forgózsámoly valamint a rajta ülő személy a kezében tartott abronccsal együtt forgásba jön, amikor az abroncsot a kísérletező elforgatja. A zsámoly szögsebessége attól függ, mekkora mértékben és milyen irányba fordította el az abroncsot maga előtt.
Magyarázat: Azzal, hogy előre felpörgetett abroncsot adtunk a kísérletező személy kezébe, a zsámolyból, a kísérletező személyből és az abroncsból álló rendszernek a kezdeti impulzusmomentuma már nem nulla. Ennek az értéknek ebben az esetben is meg kell maradnia az előző kísérletekben leírtak miatt.
Amikor a kísérletező személy elforgatja az abroncsot, azzal az abroncs impulzusmomentum vektora is elfordul. Ezért a zsámoly annak megfelelően jön forgásba, hogy az eredő impulzusmomentum a kezdeti érték legyen.
Kísérlet: Egy játék mozdonyt egy kör alakú kereten lévő sínre helyezünk. A keret a függőleges tengelye körül gyakorlatilag elhanyagolgató súrlódással tud forogni. A mozdonyban lévő rugót felhúzzuk. Ezután ügyelve arra, hogy ne lökjük meg a mozdonyt, elfordítjuk a rugót rögzítő kallantyút, és ekkor a mozdony elindul a sínen.
Megfigyelés: A mozdony az óramutatóval egyező irányba elindul. Láthatjuk, hogy ugyanekkor a sín viszont ellentétes irányú forgásba kezd.
Magyarázat: A jelenséget ismét az impulzusmomentum-tételét használva magyarázzuk meg.Ebben a kísérletben is a külső erők forgatónyomatéka zérus a keret függőleges forgástengelyére nézve, így az impulzusmomentum-tétele alapján a mozdony és a sín alkotta mechanikai rendszer impulzusmomentumának állandónak kell lenni.
Mivel kezdetben a mozdony és a sín is nyugalomban volt, így a teljes rendszer impulzusmomentuma zérus. Azzal, hogy a mozdony az óramutató járásával egyező irányba elindult, a mozdonynak a keret forgástengelyére vonatkozóan lett impulzusmomentuma. Ez vektori jellegét tekintve a mozgásirány miatt függőlegesen lefelé mutat. Ahhoz, hogy a mozdony és a keret alkotta rendszer impulzusmomentuma továbbra is zérus maradjon, a sínnek az óramutató járásával ellentétes irányba kell forognia. Ekkor a sín impulzusmomentum vektora függőlegesen felfelé mutat. Így teljesülhet, hogy az eredő impulzusmomentum zérus marad.
Kísérlet: A filmen egy olyan pörgettyű mozgását figyelhetjük meg, amit speciális körülmények között rögzítettek, foglaltak keretbe. Ezt nevezik Cardano-féle felfüggesztésnek. Ekkor a pörgettyű tömegközéppontja éppen a felfüggesztés centrumában van. Így lesz ez ún. erőmentes pörgettyű. A pörgettyű gyors forgásba hozható egy tengely körül. Ez a tengely egy olyan keretbe van foglalva, ami a pörgettyű tengelyére merőleges tengely körül tud szabadon forogni. Ezzel a kerettel is meg van ismételve az előző megoldás a harmadik merőleges tengelyt tekintve. Egy nagy fordulatszámú villanymotor segítségével gyors forgásba hozzuk a pörgettyűt.
Megfigyelés: A legkülső keretet a tér bármely irányába elforgatva azt tapasztaljuk, hogy a pörgettyű a tanteremhez képest megtartja azt a helyzetét, amiben gyors forgásba hoztuk.
Magyarázat: A pörgettyű impulzusmomentuma, amint forgásba hoztuk, zérustól különbözik (1.4.1. ábra). A Cardano-féle felfüggesztés garantálja, hogy külső erővel nem tudunk forgatónyomatékot előidézni akárhogyan is forgatjuk el a legkülső keretet. Emiatt az impulzusmomentumnak meg kell maradnia. Ezt láthatjuk is a filmen, hogy mindvégig egy irányba mutat a pörgettyű forgástengelye. A jelenségnek nagyon fontos szerepe volt illetve van pl. a repülésben, hajózásban.

1.4.1. ábra Pörgettyű Cardano-féle felfüggesztésben
Kísérlet:Először felpörgetünk nagy fordulatszámra egy szimmetrikus pörgettyűt villanymotor segítségével. A forgó pörgettyűt letesszük az asztalra, gondosan ügyelve arra, hogy a szimmetriatengelye függőlegesen álljon. Ezután egy másik szimmetrikus pörgettyűvel is ugyanígy járunk el, csak őt az előző forgásban lévő pörgettyű tetejére helyezzük. Mind a két pörgettyűt az óramutatóval ellentétes irányba hoztuk forgásba.
Megfigyelés: A két pörgettyű látszólag elég stabilan egymáson forog. Ahogy az idő múlik, a szimmetriatengelyük kezd egyre jobban látható módon a függőlegestől eltérni, és a mozgásuk kezd imbolygóvá válni.
Magyarázat: Mindkét pörgettyű szimmetria- és forgástengelye valamint az impulzusmomentum vektorának tengelye is jó közelítéssel függőleges (1.4.2. és 1.4.3. ábra). Ebből következően a pörgettyűkre ható külső erők forgatónyomatéka zérus, ezért az N1 és N2impulzusmomentum vektoruk nagyságának és irányának állandónak kell lenni.

1.4.2. ábra

1.4.3. ábra
Az idő múlásával a pörgettyűk szimmetriatengelye eltér a függőlegestől. Ekkor már nem érvényes az impulzusmomentum-megmaradás törvénye, mivel az alátámasztási pontra vonatkozóan a rájuk ható nehézségi erő forgatónyomatéka nem zérus. Ekkor a súlyos szimmetrikus pörgettyűkre jellemző mozgást kezdik végezni.
Kísérlet:Egy szimmetrikuspörgettyű tengelyének egyik végét zsinórra felfüggesztjük. Nyugalmi állapotban a pörgettyű ezen a zsinóron lóg. Ezután a pörgettyűt gyors forgásba hozzuk úgy, hogy a forgástengelye merőleges legyen a függőleges tengelyre. Ezután a pörgettyűt magára hagyjuk.
Megfigyelés: A gyors forgásba hozott pörgettyű forgástengelye megtartja vízszintes helyzetét, noha tudjuk, ha nem lenne forgásban, akkor továbbra is csak lógna a zsinóron. Ezen túlmenően a pörgettyű a függőleges tengely körül körbe is jár, és eközben a zsinór nem teljesen függőleges, hanem egy kúp palástján mozog.
Magyarázat: A vízszintes tengely körül felpörgetett pörgettyű szögsebesség vektora és impulzusmomentum vektora (N) is vízszintes irányú. Mivel a forgástengelye egyik végénél függesztettük fel a pörgettyűt, ezért az mg nehézségi erő M forgatónyomaték vektora merőleges a pörgettyű szimmetriatengelyére. Az 1.4.4. ábrán látható esetben az M éppen a kép síkjára merőlegesen kifelé mutat. Az impulzusmomentum-tétele szerint kicsi Δt idő alatt az impulzusmomentum vektor megváltozása: ΔN = MΔt. Ez azt jelenti, hogy a pörgettyű forgástengelye a vízszintes síkban elfordul egy kicsit. De a forgatónyomaték vektora ekkor ismét merőleges a forgástengelyre, így tovább fordul. Végül ez egy ωp szögsebességű precessziós mozgást eredményez. Eközben a felfüggesztő zsineg nem függőleges, hanem azzal bizonyos szöget zár be. Ennek oka az, hogy a fonálerőnek a vízszintes komponense kell, hogy biztosítsa a pörgettyű tömegközéppontjának egyenletes körmozgását.
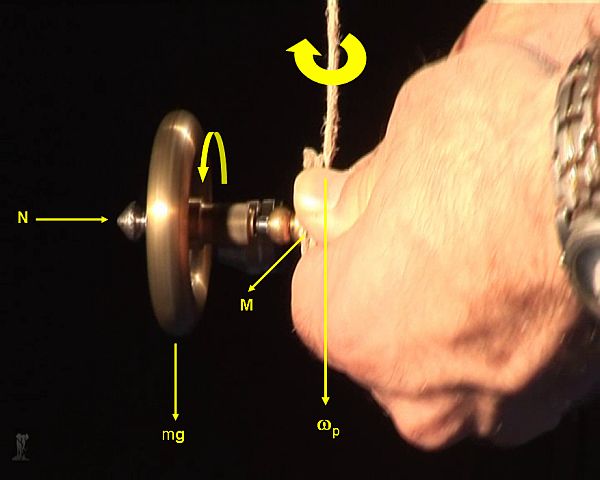
1.4.4. ábra
Kísérlet: A kísérlet megegyezik a ferde hajításnál ismertetett kísérlettel.
Megfigyelés: Azt látjuk, hogy a kocsiról kilőtt műanyag golyó parabola alakú pályán repül, és végül visszaesik a kocsira.
Magyarázat: A megfigyelt jelenség dinamikai leírásához először is koordináta-rendszert kell választanunk. A ferde hajítás korábban ismertetett leírásánál a koordináta-rendszer origóját a térnek a sín fölött lévő azon pontjához rögzítettük gondolatban, amely egybeesett a kilövő szerkezetben lévő golyó középpontjával a kilövés pillanatában. A koordináta-rendszer x-tengelye a sínnel párhuzamos, a kocsi mozgásának irányába mutat, az y-tengely pedig függőlegesen felfelé irányul. Ezt a koordináta-rendszert a továbbiakban laboratóriumi rendszernek nevezzük, és K betűvel jelöljük. Ez a vonatkoztatási rendszer jelen esetben inerciarendszernek tekinthető. A golyóra a repülés során csak a Föld mg nehézségi ereje hat (a levegő ellenállásától eltekintünk), így ebben a koordináta-rendszerben a kísérletre vonatkozóan a dinamika alapegyenlete: ma=mg.
Ahhoz, hogy meghatározzuk a golyó pályáját, az egyenletet meg kell oldanunk megfelelő kezdőfeltételekkel. Jelen esetben t=0-ban x0=0, y0=0, v0x=vk, v0y=vl., ahol vk a kocsi sebessége, v l a kilövő szerkezet által a golyónak y-irányban adott kezdősebessége. Az egyenlet megoldásából a kísérletben is látható parabola pálya adódik. Mivel a golyó helyzetét megadó x koordináta időfüggésére az egyenletből az x=v k t megoldást kapjuk, ez azt jelenti, hogy a golyó x-irányban éppen a kocsi sebességével mozog, ezért végül nyilvánvalóan visszaesik a kocsiba (1.5.1. ábra).
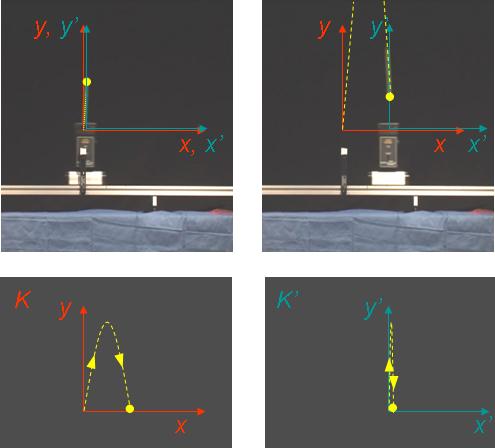
1.5.1. ábra Bár a golyó pályája a K koordináta-rendszerben és a hozzá képest egyenes vonalú egyenletes transzlációt végző K' koordináta-rendszerben különbözik, a kísérlet végeredménye mégis ugyanaz, a kiskocsiba visszaesik a golyó.
A jelenség leírásához választhatunk másik koordináta-rendszert is. Például a K' koordináta-rendszert, melynek az origóját rögzítsük a kocsin lévő kilövő szerkezet közepéhez, ami együtt fog mozogni a kocsival v k sebességgel. Vegyük észre, hogy a kilövés pillanatában K és a K' origója egybeesik. A K' koordináta-rendszer x'- és y'-tengelyének irányítását válasszuk úgy meg, hogy az x'-tengely essen egybe az x-tengellyel, míg az y'-tengely legyen párhuzamos az y-tengellyel. A koordináta-rendszerek ezen választása azt eredményezi, hogy a K' rendszer a K-hoz viszonyítva egyenes vonalú, egyenletes transzlációt végez x-irányban vk sebességgel.
A Galilei-féle relativitási elv szerint az egymáshoz képest egyenes vonalú egyenletes transzlációt végző koordináta-rendszerek a mechanikai jelenségek leírása szempontjából teljesen egyenértékűek, azaz, ha az egyik rendszer inerciarendszer, akkor a másik is az.
A K' rendszerben, mivel a fentiek szerint inerciarendszer, a dinamika alapegyenlete alakilag hasonló a K-belihez képest, és továbbra is csak a Föld nehézségi ereje hat a golyóra: ma' = mg.
A két egyenlet megoldását tekintve a különbség a kezdőfeltételekben van. A K-rendszerben a golyó kezdősebességének vektora az x-tengellyel α szöget zár be, míg a K'-rendszerben függőlegesen felfelé irányul, azaz v' 0x =0 és v' 0y =v l . A többi feltétel ugyanaz, azaz x'0=0 és y'0=0. Megoldva az egyenletet ezekkel a kezdőfeltételekkel, a pálya alakja más lesz K'-ben. A golyó függőlegesen felemelkedik, majd visszaesik a kocsira (1.5.1. ábra). Ezt kísérletileg úgy mutathatnánk be, ha a kocsihoz rögzített kamerával filmeztük volna a golyó mozgását.
Összefoglalva, a kísérlet végeredménye, azaz, hogy az egyenletes sebességgel egyenes vonalban haladó kocsiról kilőtt golyó a repülés után visszaesik a kocsiba, független a koordináta-rendszer választásától. Azonban a golyó pályájának alakja már függ attól, hogy milyen koordináta-rendszerben vizsgáljuk a jelenséget.
Kísérlet: A kísérlet hasonló az 1.5.1. fejezetben ismertetett kísérlethez azzal a különbséggel, hogy a kocsit egy fonálra kötött nehezékkel gyorsítjuk, ahogy azt tettük az egyenletesen változó mozgás vizsgálatánál is.
Megfigyelés: A golyó pályája egy parabola, ahogy az 1.5.1. fejezetben is láttuk, azonban most a golyó a kocsi mögé esik. Mennél nagyobb a gyorsulása a kocsinak, annál nagyobb az útkülönbség a golyó becsapódási helye és a kocsinak a golyó becsapódásának pillanatában elfoglalt helyzete között.
Magyarázat: A jelenséget ismét két koordináta-rendszerben írjuk le. A két koordináta-rendszer origójának és tengelyének rögzítése egyezzen meg az 1.5.1. fejezetben alkalmazottakkal. Ily módon most is K jelöli a teremhez képest nyugvó koordináta-rendszert, melyet laboratóriumi koordináta-rendszernek is hívunk. Ezt a koordináta-rendszert inerciarendszernek tekinthetjük. A kocsihoz rögzített K'-rendszer a K-hoz képest az 1.5.1. fejezethez hasonlóan egyenes vonalú mozgást végez, de most nem egyenletes sebességgel, hanem egyenletesen gyorsulva halad (1.5.2. ábra). Ez azt eredményezi, hogy a K' koordináta-rendszer nem inerciarendszer.
Míg a K rendszerben a golyó mozgását meghatározó dinamika alapegyenlete ma = mg alakú, addig a K' rendszerben, mely nem inerciarendszer, ma = mg + Fteh alakú, azaz a nehézségi erő mellett fellép az Fteh=-mak tehetetlenségi erő is, ahol ak a kocsi és ennél fogva a K' rendszer gyorsulása a K-hoz viszonyítva.
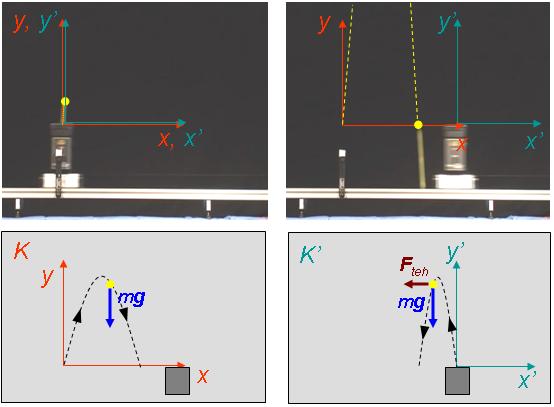
1.5.2. ábra Az egyenletesen gyorsuló mozgást végző kocsiból kilőtt golyó parabola alakú pályán repül, és a becsapódásakor a kocsi mögé esik. Míg a kísérlet eredménye független a koordináta-rendszer választásától, addig a golyó pályája illetve a ráható erők viszont függenek tőle.
A K rendszerbeli megfigyelő szerint a dinamika alapegyenletének megoldásából adódik, hogy a golyó parabola pályán repül. Továbbá a golyó helyzetét megadó x-koordináta időfüggésére x=v k0 t összefüggést kapjuk, ahol v k0 a kocsi sebessége a golyó kilövésekor, azaz a t=0-ban. Mivel a kocsi gyorsul, azaz sebessége időben folyamatosan nő, így nyilvánvaló, hogy a kocsi mögé esik a golyó.
A K'-beli megfigyelő viszont úgy magyarázza a jelenséget, hogy a golyó függőlegesen felfelé repül ki a kilövő szerkezetből, de rá nemcsak az mg nehézségi erő, hanem egy az x-tengellyel ellentétes irányba mutató erő is hat, ami a golyót a -x-irányba gyorsítja, és ezért esik a golyó a kocsi mögé.
Összefoglalva, a kísérlet végeredménye, azaz, hogy az egyenes vonalú egyenletesen gyorsuló mozgást végző kocsiról kilőtt golyó a repülése végén a kocsi mögé esik, a koordináta-rendszer választásától függetlenül ugyanaz. Azonban a golyó pályája illetve a jelenség magyarázata már függ attól, hogy milyen koordináta-rendszerben vizsgáljuk.
Kísérlet: Hajtsuk végre most úgy az előbbi kísérletet, hogy a sín a vízszintessel néhány fokos szöget zár be, azaz egy lejtőn gurul lefelé a kocsi! A lejtő dőlésszögét nagyjából akkorának válasszuk, hogy mire a kocsi a lejtő aljára ér, addigra a golyó is visszaeshessen a kocsira!
Megfigyelés: A golyó a kilövés után parabola pályán repül, és bár a kocsi egyenletesen gyorsuló mozgást végez, mégis az előbbi kísérlettel ellentétben visszaesik a golyó a kocsiba.
Magyarázat: Azáltal, hogy a sínt egy kis szögben megdöntöttük, biztosítottuk azt, hogy a kocsi egyenletesen gyorsuló mozgást végezzen. Az előbbi kísérlet alapján azt vártuk volna, hogy a kocsiról kilőtt golyó ismét nem esik vissza a kocsiba. Azonban ennek az ellenkezőjét tapasztaltuk. A jelenséget ismét két koordináta-rendszerben írjuk le. Az egyik legyen a laboratóriumi, azaz a teremhez képest nyugvó, koordináta-rendszer (K), a másik pedig a kocsihoz rögzített, a K-hoz képest egyenes vonalú egyenletesen gyorsuló mozgást végző K' rendszer (1.5.3. ábra). A K rendszer megválasztásánál a koordináta-rendszer origóját a térnek a sín fölött lévő azon pontjához rögzítjük gondolatban, amely egybeesik a kilövő szerkezetben lévő golyó középpontjával a kilövés pillanatában. A koordináta-rendszer x-tengelye a sínnel párhuzamos, a kocsi mozgásának irányába mutat, az y-tengelye pedig a sínre merőleges, és felfelé néz. Ez a vonatkoztatási rendszer inerciarendszernek tekinthető.
A K' koordináta-rendszer megválasztásánál is a korábbiakhoz hasonló módon járunk el, azaz a mérés kezdetekor a K és a K' origója essen egybe, és a K' origója a kocsival együtt mozog. Az x- illetve az x'-tengely a kísérlet során végig egybeesik, míg az y- és az y'-tengely csak a mérés kezdetekor esik egybe, utána már csak az mondható el róluk, hogy egymással párhuzamosak.
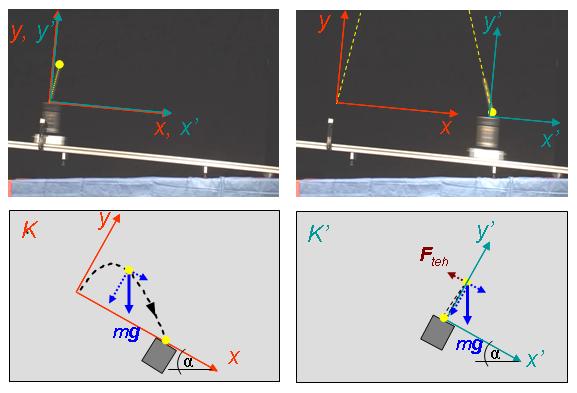
1.5.3. ábra A lejtőn leguruló, egyenletesen gyorsuló mozgást végző kocsiból kilőtt golyó a becsapódásakor a kocsiba esik vissza Míg a kísérlet eredménye független a koordináta-rendszer választásától, addig a golyó pályája illetve a ráható erők viszont függenek tőle.
A K rendszerben a golyóra vonatkozóan a dinamika alapegyenlete ma=mg alakú, ha a közegellenállási erő elhanyagolható. A K-rendszerbeli megfigyelő szerint a dinamika alapegyenletének megoldásából adódik, hogy a golyó parabola pályán repül. Az előbbi kísérlettel összevetve, most a K koordináta-rendszer 1.5.3. ábra szerinti megválasztása miatt, a nehézségi erőnek van az x-tengely irányába eső vetülete (mgsin(α)). Így x-irányban is gyorsul a test, méghozzá a x =gsin(α) -val. Ez a gyorsulás viszont éppen megegyezik a kocsi gyorsulásával, ha a kocsi kerekei és a sín közötti súrlódás, valamint a kocsi kerekeinek tömege a kocsi teljes tömegéhez képest elhanyagolható. Mivel a kocsi sebessége és a golyó x-irányú (lejtő irányú) kezdősebessége, valamint az x-irányú gyorsulásuk is megegyezik, így a golyó visszaesik a kocsira.
A K' rendszerben vizsgálva a jelenséget, a nehézségi erő mellett fellép az Fteh=-mak tehetetlenségi erő is, ahol ak a kocsi és ennél fogva a K' rendszer gyorsulása a K-hoz viszonyítva. Így a dinamika alapegyenlete a golyóra vonatkozóan ebben a koordináta-rendszerben ma = mg + Fteh alakú. A K'-beli megfigyelő ezért úgy magyarázza a jelenséget, hogy a golyó az y'-tengely irányában felfelé repül ki a kilövőszerkezetből. A golyó x'-tengely menti mozgását két erő határozza meg. Egyrészt hat rá a nehézségi erő x'-tengely irányú, mgsin(α) nagyságú komponense. Másrészt hat vele ellentétes irányban az Fteh tehetetlenségi erő, aminek a nagysága szintén mgsin(α). Mivel a két erő eredője így 0, és a golyó v'x0 kezdősebessége 0, így a mozgás során x'-irányban a golyó nem mozdul el. Ezért esik vissza végül a golyó a kocsiba.
Összefoglalva, a kísérlet végeredménye, azaz, hogy a lejtőn lefelé guruló kocsiról kilőtt golyó a repülése végén a kocsiba visszaesik, a koordináta-rendszer választásától függetlenül ugyanaz. Azonban a golyó pályája, illetve a jelenség magyarázata már függ attól, hogy milyen koordináta-rendszerben vizsgáljuk.
Kísérlet: A kísérlet megegyezik az 1.2.3. fejezetben a körmozgás dinamikája kapcsán már ismertetett kísérlettel. Ahhoz, hogy lássuk, hogy a kúpingával együttforgó megfigyelő mit látna, egy kamerát kellene elhelyezni az inga fölé, ami együtt forogna vele. Ez technikailag nehezen megoldható. Ezért egy animáción mutatjuk be, hogy mit látna az inga felett a teremhez képest nyugvó helyzetben lévő megfigyelő illetve az ingával együtt forgó megfigyelő. Az animáción a fekete vonalak a teremhez rögzített K koordináta-rendszernek a tengelyeit jelölik, melyeket képzeletben az inga alatt a padlóra rajzoltunk.
Megfigyelés: A teremhez képest nyugvó megfigyelő azt látja, hogy a fonál végén lévő golyó, miután meglöktük, egyenletes körmozgást végez. Az ingával együtt forgó megfigyelő viszont úgy látja, hogy a golyó végig nyugalomban van, és alatta a K koordináta-rendszer tengelyei fordulnak el.
Magyarázat: Az 1.2.3. fejezetben már tárgyaltuk a kúpinga mozgásnak dinamikai leírását inerciarendszerben, azaz a teremhez rögzített K koordináta-rendszerben. Ebben a fejezetben viszont az ingával együttforgó rendszerből, azaz egy nem-inerciarendszerből írjuk le a mozgást, kiemelve a különbséget a két leírási mód között. Ha egy inerciarendszerhez képest ω szögsebességgel forgó koordináta-rendszerben akarjuk alkalmazni a dinamika alapegyenletét egy m tömegű test mozgásának leírására, akkor az inerciarendszerben fellépő erőkhöz hozzá kell adnunk egy radiálisan kifelé irányuló Fcf=mω2r tehetetlenségi erőt, az ún. centrifugális erőt, ahol r a koordináta-rendszer origójából a testhez húzott helyvektor.
Ennek alapján az ingával együtt forgó koordináta-rendszerben a golyóra az inerciarendszerbeli két erőn, az mg nehézségi erőn és a K kötélerőn kívül hat egy harmadik erő, a Fcf centrifugális erő is (1.5.4. ábra). Az erők irányát tekintve az mg függőlegesen lefelé, a K értelemszerűen a kötél irányában a felfüggesztési pont felé, míg az Fcf centrifugális erő vízszintesen sugárirányban kifelé mutat. Az 1.2.3. fejezetben leírtak szerint itt is bontsuk fel a kötélerőt vízszintes és függőleges irányú összetevőkre. Mivel a fonál végén lévő test függőleges irányban nem gyorsul, így az erők eredőjének függőleges irányban zérusnak kell lenni: mg=Kcosφ. Vízszintes irányra vonatkozóan a dinamika alapegyenlete az inerciarendszerben felírt alaktól eltér, mivel a kötélerő Ksinφ komponensén kívül a forgó vonatkoztatási rendszerben fellép az előzőekben említett centrifugális erő is. Az 1.2.3. fejezetben láttuk, hogy a kötélerő vízszintes irányú összetevőjének nagysága Ksinφ =mrω2, azaz megegyezik a centrifugális erő nagyságával. Ebből következően az eredőjük, mivel ellentétes irányúak, zérus, azaz a testnek nincs vízszintes irányban sem gyorsulása. Tekintettel arra, hogy a kísérlet kezdetén a forgó rendszerből nézve a test nyugalomban volt, így ahogy az animációban is látható, végig nyugalomban is marad.
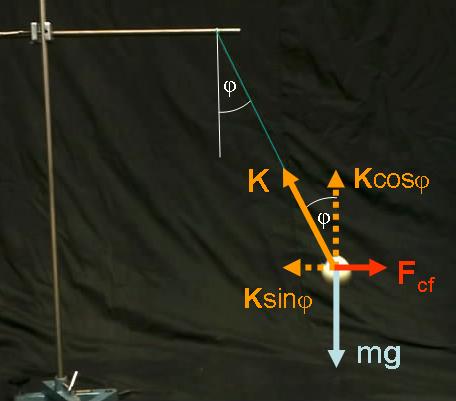
1.5.4. ábra A fonál végén lévő m tömegű golyóra ható erők az ingával együttforgó vonatkoztatási rendszerben
Kísérlet:Egy korongra ráerősítünk egy gumicsövet, melyen vizet áramoltatunk keresztül állandó sebességgel (1.5.5. ábra). A korongot egy villanymotor forgatja egy vízszintes tengely körül, azaz a korong síkja függőleges. (Természetesen a kísérlet vízszintes síkban forgó koronggal is ugyanígy elvégezhető lenne.) A korongon van egy lyuk, melyen egy kis teljesítményű diódalézerrel átvilágítunk. A divergens lézernyaláb egy síktükörről a korong közepére verődik vissza. Így jól láthatóvá válik majd a cső közepének elmozdulása, mivel a kísérletet a jó láthatóság miatt gyenge laboratóriumi megvilágítás mellett végezzük, csaknem sötétben. Ily módon csak akkor kap fényt a korong közepe, azaz akkor válik láthatóvá a kamera számára illetve számunkra, amikor a lyuk a lézernyaláb elé kerül. Ezzel a módszerrel elérjük azt, hogy csak akkor látszódik a cső alakja a filmen, amikor a cső befolyónyílása (A) felül van és a kifolyónyílása (B) pedig alul úgy, hogy a be- és kifolyó nyílást összekötő egyenes függőleges (1.5.5.b ábra). Megjegyezzük, hogy a kísérleti eszköz olyan kiképzésű , hogy a teljes kísérlet alatt a koronggal együtt forgó A pontból a szintén a koronggal együtt forgó B pont felé folyik a víz. Az előzőekben leírt stroboszkópikus hatás miatt fogjuk csak látni a csövet mindig függőleges helyzetben.
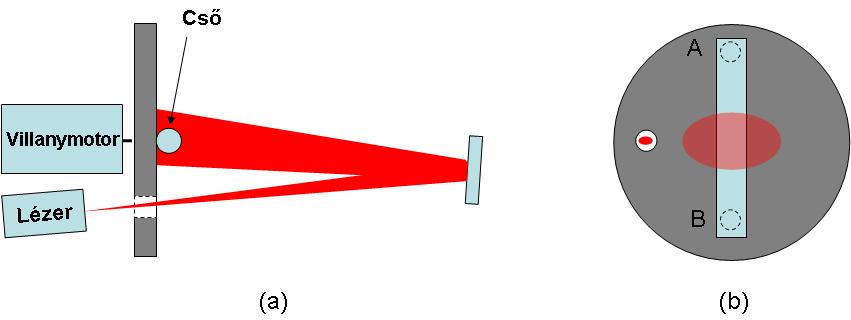
1.5.5. ábra A kísérleti elrendezés (a) felülnézetben és (b) szemből. Ez utóbbi esetben a tükröt nem mutatjuk
Megfigyelés:

1.5.6. ábra (a) Amikor a korong nem forgott, akkor az áramló vízzel teli cső a korongnak az ábra síkjára merőleges irányú forgástengelye felett volt. (b) Amikor a korong az óramutató járásával megegyező irányban forgott, az áramló vízzel teli csőnek a korong középső részén lévő szakasza a megvilágítás pillanatában a forgástengelytől jobbra, (c) míg a korong forgásirányának megváltoztatása után balra tolódott el.
Magyarázat: Egy inerciarendszerhez képest ω szögsebességgel forgó rendszerben az m tömegű, a forgó rendszerhez viszonyítva v sebességgel mozgó testre a centrifugális erőn kívül egy másik tehetetlenségi erő is hat, amely merőleges a test sebességére és a forgástengelyre: FC = 2mvxω. Ezt az erőt Coriolis-erőnek nevezzük. Vegyük észre, hogy ennek az erőnek a kifejezésében a v és az ω vektori szorzata szerepel.
Amikor nem forog a korong, akkor a koronghoz rögzített vonatkoztatási rendszer is inerciarendszernek tekinthető, így a csövön átfolyó vízre nem hatnak tehetetlenségi erők, melyek a vizet oldalirányba eltéríteni akarnák. Ezért a cső a korong forgástengelye felett halad át akkor, amikor éppen a be- és kifolyónyílás egymás felett van (1.5.7. ábra). Ekkor a vízre illetve a csőre ható nehézségi erő is függőleges irányú, így nem deformálják a cső alakját. Továbbá a víz nyomásából származó nyomóerők a cső keresztmetszetében mindenhol egyenlő mértékben hatnak a cső falára, így nem okoznak a csövön a függőleges iránytól való egyoldalú eltérést.

1.5.7. ábra Amikor nem forog a korong, a cső a korong forgástengelye felett halad át
Ha el kezdjük forgatni a korongot ω szögsebességgel, akkor a koronghoz rögzített koordináta-rendszer ω szögsebességgel forog a teremhez rögzített, inerciarendszernek tekinthető koordinátarendszerhez képest. A fentiek szerint ekkor a korongra erősített csőben áramló vízrészecskékre az inerciarendszerben fellépő erőkön kívül nemcsak a centrifugális, hanem a Coriolis-erő is hat. A jelenség magyarázata a cső teljes hosszúságára túlmutat jelen tananyag keretein, ezért csak a forgástengely magasságában lévő kicsiny csőhossz torzulásáért felelős erőket ábrázoljuk az 1.5.8. és 1.5.9. ábrákon. Természetesen a csőben áramló minden részecskére hatnak ezek az erők, nem csak azokra, akik a képen látható középpontban vannak éppen. Ezek együttes hatására veszi fel az egész cső az adott görbe alakot. Felhívjuk a figyelmet, hogy a centrifugális erő kifejezésében szereplő sebesség, a tömegpontnak a kerületi sebessége, míg az ábrán jelölt v vektor viszont a vízrészecskéknek a forgó rendszerbeli sebességét jelöli.

1.5.8. ábra Ha a korong az óramutató járásával megegyező irányban forog, akkor az ω szögsebesség vektor az ábra síkjára merőlegesen befelé mutat. Mivel a vízrészecskék a megvilágítás pillanatában éppen függőlegesen lefelé haladnak, így a rájuk ható Coriolis-erő jobbra mutat. A forgástengely magasságában a vízrészecskékre ható centrifugális erő is vízszintes irányú. Ezért a cső középső szakasza a korong forgástengelyétől jobbra tolódik el egészen addig, míg a cső anyagában ébredő deformációs erők ki nem egyenlítik a Coriolis-erő és a centrifugális erő hatását.
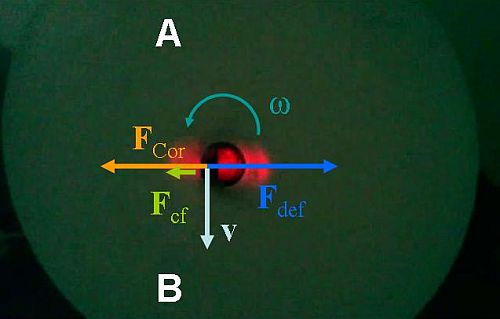
1.5.9. ábra Ha a korong az óramutató járásával ellenkező irányban forog, akkor az ω szögsebesség vektor az ábra síkjára merőlegesen kifelé mutat. A vízrészecskék a megvilágítás pillanatában függőlegesen lefelé haladnak, így a rájuk ható Coriolis-erő balra mutat. A forgástengely magasságában a vízrészecskékre ható centrifugális erő is vízszintes irányú. Ezért a cső középső szakasza a korong forgástengelyétől balra tolódik el egészen addig, míg a cső anyagában ébredő deformációs erők ki nem egyenlítik a Coriolis-erő és a centrifugális erő hatását.
Kísérlet:A kísérleti eszköz egy csapágyazott függőleges tengely körül, vízszintes síkban forgatható korongból áll, amelyhez fémkeretet erősítettünk (1.5.10. ábra). A keretről lóg le az inga, melynek a nehezéke egy kis fém tégely az alján egy pici lyukkal.A kísérlet előtt a tégelybe homokot teszünk. Az ingát oldalra kitérítjük, majd elengedjük. Néhány lengés után a keretet meglökjük úgy, hogy az óramutató járásával megegyező irányban forog. Figyeljük meg, hogy milyen mintázatot rajzol le a tégelyből kiszóródó homok a korongon!
Ha rászerelnénk egy kamerát a keret tetejére, akkor bemutathatnánk azt is, hogy a forgó rendszerbeli megfigyelő hogyan látja az inga mozgását. Ezt most egy animációval helyettesítjük. Az animáció bal oldalán a korongra felülről ránéző, a teremhez képest nyugvó megfigyelő által látottakat mutatjuk, míg a jobb oldalon a keretről lenéző megfigyelő szemszögéből látható mozgást mutatjuk be.

1.5.10. ábra A kísérleti eszköz
Megfigyelés: A kísérlet elején, amikor a keret még nem forgott, csak az inga lengett, akkor a tégelyből a homok egy egyenes mentén szóródott ki. Amikor elkezdett forogni a keret, akkor a kiszóródó homok egy rozettamintázatot kezdett kirajzolni. A tengely csapágyazásánál fellépő súrlódás miatt néhány forgás után láthatóan csökkent a keret szögsebessége, és ekkor a rozetta ún. levelei vékonyodni kezdtek.

1.5.11. ábra Az inga lengése során a tégelyéből kiszóródó homokkal a forgó korongra egy rozettamintázatot rajzol
A teremhez képest nyugvó megfigyelő úgy látja, hogy az inga végig ugyanabban a síkban leng, és a korong fordul el alatta, míg a keretről lenéző megfigyelő viszont azt látja, hogy a korong áll, és az inga végez fura, rozettaszerű mozgást.
Magyarázat: Írjuk le a jelenséget először a teremhez rögzített K koordináta-rendszerben, mely inerciarendszernek tekinthető. Ebben a rendszerben az inga tégelyére ható erők az mg nehézségi erő és az Ff fonálerő (1.5.12. ábra). A nehézségi erőt bontsuk fel fonálirányú (mgcosφ) és a fonálra merőleges (mgsinφ) komponensekre. A fonálra merőleges irányra, azaz a pálya érintőjének irányára vonatkozóan a dinamika alapegyenlete: -mgsinφ=mat, ahol at a tangenciális gyorsulás. A negatív előjel arra utal, hogy az ingára ható erők eredője mindig a kitéréssel ellentétes irányú. Ha kicsi a φ szögkitérés, akkor ezen egyenlet megfelelő átalakításával megmutatható, hogy az inga harmonikus rezgőmozgást végez egy adott síkban. Ezért a kísérlet elején, amikor nem forgott a korong, a tégelyből kiszóródó homok egy egyenest rajzolt. Ez az egyenes nem más, mint ahol az inga lengési síkja elmetszi a korong síkját. Amikor a korongot megforgattuk, akkor azért kaptuk a rozetta mintázatot, mert az ingára továbbra is ugyanaz a két erő hatott csak, így a lengési síkja nem változott, viszont a korong elfordult alatta.
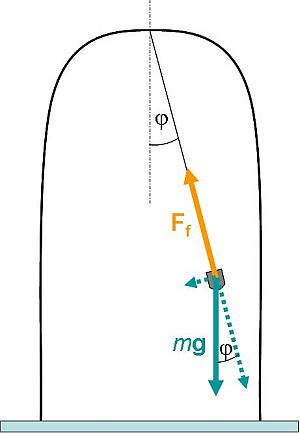
1.5.12. ábra Az inga homokkal teli tégelyére ható erők a K koordináta-rendszerben
Ezután írjuk le a jelenséget a koronggal együttforgó megfigyelő szemszögéből, azaz a forgó koronghoz rögzített K' koordináta-rendszerből. Mivel a K' rendszer a K-hoz képest ω szögsebességgel forog, és a K' rendszerben is leng az inga, így ahogy az előbbi fejezetben is már szó volt róla, az inerciarendszerbeli erőkön kívül az inga tégelyére két tehetetlenségi erő is hat, a centrifugális erő és a Coriolis-erő (1.5.13. ábra), melyek közül a Coriolis-erő a meghatározó.
A K' rendszerbeli megfigyelő tehát úgy értelmezi a jelenséget, hogy az inga két szélső helyzet között leng, amit a fonálerő és a nehézségi erő (azaz az inerciarendszerben is fellépő erők) okoznak. Azonban a K' rendszerben az inga tégelyére hat még két tehetetlenségi erő, a centrifugális erő és a Coriolis-erő. Ezen erők eredője, figyelembe véve a Coriolis- és a cetrifugális erők irányáról tanultakat, jelen esetben közel merőleges az inga sebességvektorára, és balra mutat. Ebből következően az inga miközben halad előre, közben balra is elmozdul, és így aztán kialakul a rozettamintázat. Azért, hogy jobban lássuk a különbséget, amelyet a két megfigyelő lát, nézzük meg egy animáción a K és a K'-beli megfigyelő szemszögéből a jelenséget egyidejűleg.
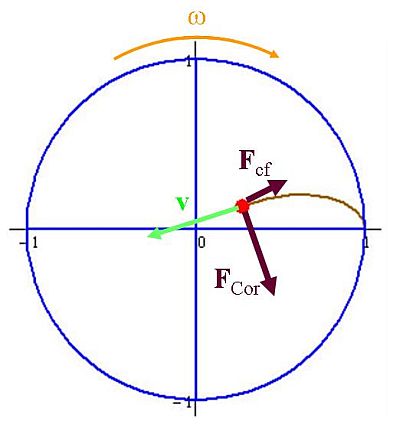
1.5.13. ábra A K' rendszerben az inga homokkal teli tégelyére ható tehetetlenségi erők, ha ω állandó
Ahogy a megfigyeléseknél is már utaltunk rá, a korong néhány forgás után láthatóan lassult, és a rozettamintázat torzulni kezdett. Mivel mindkét tehetetlenségi erő függ a K' rendszer ω szögsebességétől, így ha lassul a rendszer forgása, akkor csökken a nagyságuk. Azonban a számítások szerint ilyenkor még egy harmadik tehetetlenségi erő is fellép (Fβ = mrxβ), ahol β a forgó rendszer szöggyorsulása (1.5.14. ábra). Azért, hogy jobban lássuk a különbséget, amelyet a két megfigyelő lát, nézzük meg ismét egy animáción a K és a K'-beli megfigyelő szemszögéből a jelenséget egyidejűleg, és hasonlítsuk össze a kísérlettel!
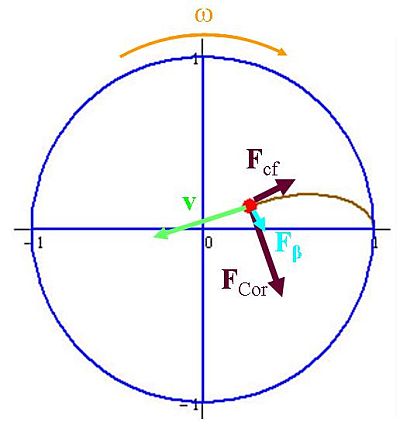
1.5.14. ábra Ha a forgó koordináta-rendszer β szöggyorsulása nem zérus, akkor a K' rendszerben az inga homokkal teli tégelyére nemcsak a Coriolis-erő és a centifugális erő hat, hanem egy harmadik tehetetlenségi erő (Fβ) is
Kísérlet:Borotvapengét, varrótűt helyezünk a víz felszínére óvatosan úgy, hogy nehogy átszúrjuk a rugalmas felületi réteget. A kísérletet könnyebb elvégezni, ha vékony zsírréteg is van a fémtárgyak felületén.
Megfigyelés:

1.6.1. ábra A víz felszínére helyezett borotvapenge, varrótű nem merül el, pedig sűrűsége nagyobb, mint a vízé. Úgy fekszenek a kissé benyomódott felszínen a tárgyak, mint egy kifeszített rugalmas hártyán. A hidrosztatika törvényeinek ellentmond ez a tapasztalat.
Magyarázat: A folyadék szabad felszíne másként viselkedik, mint azt a hidrosztatikai törvények alapján várni lehetne. A folyadékot alkotó molekulák között rövid hatótávolságú vonzó erő hat. Azonos molekulák közötti erőt kohéziós erőnek, különböző molekulák között fellépőt adhéziós erőnek nevezzük. A folyadék belsejében lévő molekulánál a körülötte lévő molekulák hatása kiegyenlítődik, míg a felületen lévő molekula köré rajzolt gömbnek csak egy részét (felét) töltik ki folyadékmolekulák, a szabad felszín felől sokkal kevesebb molekula hat rá. Ezzel magyarázható a rugalmas hártyaként viselkedő felületi réteg kialakulása. A molekuláris erők eredője függ a bemerülő testet határoló görbe hosszától és a folyadék benyomódásától.
Kísérlet:Egy kör alakú alumínium lemezt helyezünk a víz felszínére óvatosan. Ezután fém anyacsavarokat, mint nehezéket pakolunk rá.
Megfigyelés:

1.6.2. ábra A 14 cm átmérőjű korong az elsüllyedése előtt 15 darab 2 g-os anyacsavart is elbírt.
Magyarázat: Számoljon utána, mekkora alumínium korongot érdemes kiszabni egy 0,8 mm vastag lemezből, hogy a vízmolekulák között ébredő erő megtartsa azt a víz felületén. A számolásból alig több mint 1 cm adódik a korong átmérőjére. A filmen látható kísérletben a felületi rétegben ébredő, függőlegesen felfele mutató, a korong kerületével arányos, Ffel=α2rπ≈0,032 N nagyságú eredő erő lényegesen kisebb, mint a korongra és az anyacsavarokra ható Fn=mösszg≈0,61 N nehézségi erő. Az értelmezéshez nézzük meg jobban a kialakuló folyadékfelszínt, és keressünk még egy erőt, melyet eddig figyelmen kívül hagytunk!
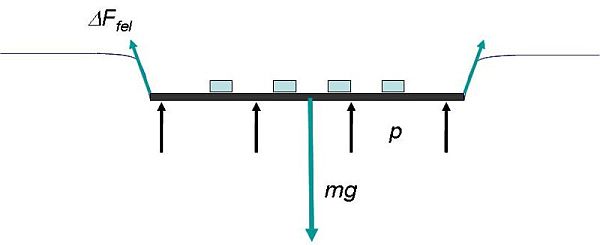
1.6.3. ábra A kísérlet modellje, a lemezre ható erőkkel.
Kísérlet:Egy dinamóméterre egy korongot függesztünk, majd a korongot óvatosan ráhelyezzük a víz felszínére. Ezután el kezdjük a dinamómétert felfelé emelni, és megnézzük, hogy mekkora erő kell ahhoz, hogy a korong elszakadjon a víztől. A kísérletet megismételjük mosószeres vízzel is.
Megfigyelés: Ha a víz felszínére helyezett korongot el akarjuk emelni a felületről, akkor a zsíroktól megtisztított korong vizes marad a kiemelés után is. A kiemeléshez erőre van szükség. A kiemeléshez szükséges erőt a dinamométerről olvashatjuk le. Itt nem történt pontos mérés, de azt jól láthatjuk, hogy a mosogatószeres vízből a korong kiemeléséhez kisebb erőre van szükség. A mosószer csökkenti a felületi feszültséget.

1.6.4. ábra A korong kiemeléséhez erőre van szükség.
Magyarázat: A mosószeres vízben a molekulák között ható erő kisebb, mint a tiszta vízben.
Kísérlet:Egy kör alakú drótkeretet, melyhez egy cérnahurkot is kötöttünk, belemártunk folyadékba, majd kiemeljük belőle. A drótkarikán vékony folyadékhártya képződik úgy, hogy a cérnahurok alakja szabálytalan.
Megfigyelés:

1.6.5. ábra A hurok kör alakra feszül ki. A hártyában lévő cérnakarika belsejét kitöltő hártya kilyukasztásakor a cérnahurkot a folyadék megmaradt része kifeszíti.
Magyarázat: A megfigyelésből arra következtetünk, hogy a hártyában olyan összehúzó erők működnek, melyek a határoló görbére merőlegesek.
Kísérlet:Két pálcát kössünk össze azonos hosszúságú fonállal! Készítsünk folyadékhártyát*, a fonalak körívben határolják a hártyát, ezzel kicsit megemelik az alsó pálcát.
Megfigyelés:

1.6.6. ábra Ha kilyukasztjuk a hártyát, az alsó pálca kicsit lejjebb kerül. A kísérlet közben megfigyelhetők az egyre vékonyodó folyadékhártyán az egyenlő vastagság görbéi is.
Magyarázat: A folyadék felületét csak úgy növelhetjük meg, ha a folyadék belsejéből újabb és újabb molekulákat juttatunk a felületre. A molekula kiemelése közben a felületi rétegben munkát kell végezni a folyadék belsejébe mutató erő ellen. A végzett munka árán növekszik a felület, és nő a folyadék energiája. Megmutatható, hogy a folyadékhártya energiája arányos a hártya felületével. Gondoljuk el, hogy az alsó pálcát addig húzzuk lefele, amíg a fonalak is egyenesek lesznek. Majd engedjük el az alsó pálcát. Ha összehúzódik a folyadék felülete, csökken a felületi energia, ezzel párhuzamosan felemeli az alsó pálcát, aminek nő a magassági energiája. Lesz egy egyensúlyi helyzet, amikor a két energia összege minimális. Ha a hártyát kilyukasztjuk, a pálca lejjebb süllyed.
A kísérlet elvégzése közben egy optikai jelenséget is megfigyelhetünk. A folyadékhártya egyre vékonyodik, és amikor már csak néhány hullámhossznyi a vastagsága, akkor az első és a hátsó felületéről visszaverődő fény interferenciára képes. Az így keletkező mintázatot egyenlő vastagság görbéinek nevezzük.
Kísérlet: Készítsünk folyadékhártyát* a drótkereten, a benne lévő fonal lazán, feszítetlenül helyezkedik el.
Megfigyelés:

1.6.7. ábra Ha az egyik oldalán kilyukasztjuk a folyadékhártyát, akkor a másik oldalon a hártya összehúzódik és a fonal kör alakúra feszül ki.
Magyarázat: Ekkor a legkisebb a megmaradt hártya területe. A fonal súlya elhanyagolható, a magassági energiája kicsi. Ezért a rendszer energiájának jelentős részét a felületi energia adja.
Kísérlet: A keret belsejében van egy oldal, amely elmozdítható. Kezdetben készítünk egy szappanhártyát a teljes kereten. Ekkor a belsejében lévő, elmozdítható oldal nem mozog. A keret helyzete miatt a nehézségi erő és a külső keretben ébredő tartóerő kiegyenlítik egymást.
Megfigyelés:

1.6.8. ábra Ha kilyukasztjuk az egyik oldalon lévő hártyát, akkor a megmaradt hártya összehúzódik nagyon kicsi felületűre.
Magyarázat: Kezdetben a hártya által kifejtett összehúzó erő nem mozdítja el ezt az oldalt, mert mindkét oldalán folyadékhártya van. Ha az egyik oldalon kiszúrjuk a hártyát, akkor az elmozdítható oldal egyik oldalára hat csak a felülettől erő, amely arányos az elmozdítható oldal hosszával. A gumirugalmasságtól eltérően ez az erő független a hártya területétől. Ha a keret síkját elforgatjuk, akkor meg tudjuk növelni a hártya nagyságát. Ugyanis ebben a helyzetben már a nehézségi erőt nem egyenlíti ki a keretben ébredő tartóerő.
Kísérlet:Egy drótból készült kockát a folyadékba merítünk, majd óvatosan kiemeljük belőle.
Megfigyelés:

1.6.9. ábra A folyadékból* kiemelt kockán rövid idő alatt kialakul egy felület, mely a továbbiakban stabilan megmarad.
Magyarázat: Megmutatható, hogy a kezdeti alakból a drótkeret által meghatározott határokkal bíró minimális felület jön létre.
Kísérlet:Egy kettős ívből álló drótkeretet bemártunk a folyadékba*, majd óvatosan kiemeljük belőle.
Megfigyelés:

1.6.10. ábra Drótkerettel határolt hártya keletkezik.
Magyarázat: Ez egy minimál felület.
Kísérlet: A rézdrótból készült szitán a víz átfolyik. Tegyük óvatosan a víz felszínére, a nagy sűrűségű anyagból készült szita úszik.
Megfigyelés:

(a)

(b)
1.6.11. ábra A szitán egy bizonyos mennyiség ráöntése után átfolyik a víz (a), míg a vízfelületre helyezve úszik a szita (b).
Magyarázat: Ha a szitára vizet öntünk, annak egy része a szita alá kerül. Ha ez a mennyiség növekszik, egyszer eléri azt a méretet, melyet a felületi erők már nem tudnak megtartani, és elkezd folyni a víz a szitán át. Egyenletes utántöltéssel ez a folyamatos áramlás fenntartható. Ha ráhelyezzük a szitát a víz felületére, akkor az rugalmas hártyaként viselkedik, mint pl. a borotvapenge esetén.
Kísérlet: Egy szívószál egyik végét szappanoldatba merítjük, és fújunk egy szappanbuborékot! Ezután a szívószál másik végét egy gyertya lángjához közel tesszük.
Megfigyelés: Már a fújás kifejezés is azt mutatja, hogy a buborékban nagyobb lehet a nyomás, mint a légnyomás. Van némi hasonlóság a léggömb felfújásához. Ha a szívószálat közelítjük a gyertya lángjához, csaknem elfújja azt.

1.6.12. ábra A szappanbuborékból kiáramló levegő elfújja a gyertya lángját.
Magyarázat: A buborék belsejében uralkodó túlnyomás miatt kiáramló levegő okozza a láng lobogását. A buborék belsejében azért kell túlnyomásnak lenni, hogy a hártya görbültsége miatt a felület görbültségéből eredő, a homorú felület fele mutató erővel szemben a hártya egyensúlyát biztosítsa (1.6.13. ábra). Kisebb görbület esetén az erő kisebb, ezért a görbületi nyomás is kisebb. Megmutatható, hogy a görbületi nyomás fordítva arányos a buborék sugarával.
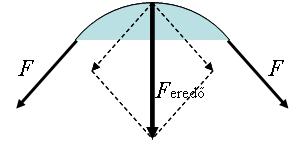
1.6.13. ábra A görbületi nyomást ellensúlyozó befele mutató erő
Kísérlet: Megfestett vízzel feltöltjük az un. kapilláris csősorozatot.
Megfigyelés: A közlekedő edényeknél tanultak szerint az edényhez csatlakozó függőleges csövekben azonos magasságúnak kellene lenni a vízszintnek. A nagy keresztmetszetű, szélső csőtől távolodva, egyre csökken a csövek átmérője, ugyanakkor a vízszint egyre magasabb áll bennük (lásd 1.6.14. ábra). A jobb megfigyelést a vízben oldott fluoreszcein segíti, mely ultraibolya fénnyel megvilágítva zöldes fényt bocsát ki.

1.6.14. ábra A nagy keresztmetszetű, szélső csőtől távolodva egyre csökken a csövek átmérője, ugyanakkor a vízszint egyre magasabb áll bennük.
Magyarázat: Ha nedvesítő folyadékot tartalmazó edénybe kis keresztmetszetű kapilláris csöveket teszünk, akkor a csövekben a külső folyadékszinthez képest a csőben magasabbra emelkedik a folyadék az 1.6.15. ábra szerint. Az emelkedés magassága fordítottan arányos a kapilláris sugarával: Δh=2α/r.A jelenséget kapilláris emelkedésnek nevezzük. A külső nagy átmérőjű tartályban lévő vízszinthez képest mérjük az emelkedést, amely a kapilláris sugarával fordítottan arányosan nő. Tiszta vízzel is elvégezhető a kísérlet, ekkor a folyadékszint nehezebben figyelhető meg.
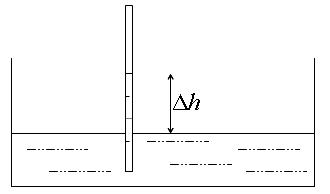
1.6.15. ábra Kapilláris emelkedés
Kísérlet: Egy szokatlan alakú edénybe öntött folyadék felszínét figyeljük meg. Az edény alaplapja egyenlő szárú háromszög és a szárszöge nagyon kicsi.
Megfigyelés: Ahol a határoló lapok távolsága nagyon kicsi, a folyadék nagyon felemelkedik, és a szabad vízfelület messze nem lesz vízszintes (1.6.16. ábra). A jobb megfigyelést a vízben oldott fluoreszcein segíti, mely ultraibolya fénnyel megvilágítva zöldes fényt bocsát ki.

1.6.16. ábra Az ék alakú edényben annál magasabban van a folyadékszint, minél vékonyabb az edény.
Magyarázat: A folyadék felületét gondolatban feloszthatjuk rövid darabokra, melyek jól közelíthetők kicsi fél hengerpalásttal. Megmutatható, hogy az emelkedés magassága az éltől mért távolsággal fordítva arányos. A folyadékfelszín üveg melletti görbéje hiperbola alakú.
*Megjegyzés: A tankönyvek a felületi feszültség tanulmányozásakor gyakran arról írnak, hogy szappanhártyákat kell készíteni. A hártyák előállításához ma már nem használunk szappant, de az elnevezést megőrizzük. A gyermek buborékfúvókhoz tartozó folyadékot használtuk a kísérleteink során, ezekből elég tartós, jó minőségű hártyákat tudtunk készíteni.
Függőleges tárcsa rögzített, jól csapágyazott, vízszintes tengely körül foroghat. A tárcsához egy spirálrugót erősítettek úgy, hogy a másik vége egy rúdhoz van erősítve, melyet egy motor segítségével harmonikusan rezgő mozgásba hozhatunk.

1.7.1. ábra A Pohl-féle készülék tápegységgel és mérőműszerekkel
Ha a rúd áll (vagyis a motor nem forog), akkor a spirálrúgó a tárcsa - egyensúlyi helyzettől mért - elfordulási szögével arányos és vele ellentétes irányú forgatónyomatékot gyakorol. Ennek következtében a tárcsa (a súrlódás hatását elhanyagolva) harmonikus forgási rezgéseket végez.
A tárcsa egy elektromágnes sarkai között forog. Amennyiben az elektromágnesen áram folyik keresztül, akkor a tárcsában örvényáram indukálódik, amely a Lenz-törvény értelmében fékezi a tárcsa mozgását. A fékező forgatónyomaték arányos a tárcsa szögsebességével, továbbá az arányossági tényező (és így a csillapodást létrehozó nyomaték) az áram erősségével szabályozható. Az áramerősségét az ábrán a szürke műszer méri.
Ha a rudat a villanymotor forgatásával harmonikus forgási rezgésbe hozzuk, akkor a spirálrúgó közvetítésével a tárcsára a motor fordulatszámával azonos frekvenciájú harmonikusan rezgő forgatónyomaték hat, amely gerjesztő hatásként kényszerített rezgésre készteti a tárcsát. A motor fordulatszáma, és így a gerjesztés frekvenciája a motor kapocsfeszültségével szabályozható. A kapocsfeszültséget a sárga mérőműszer méri a képen.
A Pohl-féle készülékkel tehát tanulmányozhatjuk a harmonikus és csillapodó forgási rezgéseket, továbbá a motor bekapcsolásával a kényszerített forgási rezgéseket is. Sőt kis módosítással anharmonikus rezgések és a rezgések kialakulásának feltételei is jól tanulmányozhatók a későbbiekben részletezett módon.
Kísérlet:A tárcsát az egyensúlyi helyzetéhez képest kitérítjük és elengedjük. Látható, hogy a tárcsa forgási rezgéseket végez az egyensúlyi helyzete körül. A kísérletet különböző nagyságú kezdeti kitérésekkel végezzük el. A kísérletek során a motor álló helyzetben van, és a tekercsen nem folyik áram, azaz a tárcsa csillapítatlan sajátrezgését vizsgáljuk.
Megfigyelés: Ha megmérjük a különböző kezdeti kitéréshez tartozó rezgések periódus idejét, akkor azt tapasztaljuk, hogy a periódus nem függ a kezdeti kitéréstől. Ez az izokronizmus a harmonikus rezgés egyik jellemző tulajdonsága. Ha megmérjük a szögelfordulás időfüggését, akkor azt tapasztaljuk, hogy a tárcsa harmonikus forgási rezgést végez.
Magyarázat: A spirálrúgó a tárcsa - egyensúlyi helyzettől mért - elfordulási szögével arányos és vele ellentétes irányú forgatónyomatékot gyakorol a tárcsára. Ennek következtében a tárcsa (a tengelynél megjelenő és a légellenállás következtében fellépő súrlódás hatását elhanyagolva) harmonikus forgási rezgéseket végez.
Kísérlet:A tárcsát az egyensúlyi helyzetéhez képest maximálisan kitérítjük és elengedjük, a tekercsen átfolyó áram erősségének különböző értékei mellett. Az áramerősségét a filmen a szürke műszer méri. Látható, hogy a tárcsa forgási rezgésének maximális kitérései idővel csökkennek, azaz a tárcsa rezgése csillapodik. A csillapodás mértéke az áram erősségégével növekszik. A kísérletek során a motor áll.
Megfigyelés: A tárcsa maximális kitérései csökkenő sorozatot alkotnak. Ha azt tapasztaljuk, hogy ez a sorozat egy mértani sorozat, akkor az arra utal, hogy a csillapodást okozó forgatónyomaték arányos a szögsebességgel.
Magyarázat: A tárcsa tekercsén átfolyó áram mágneses teret hoz létre, amelynek az erővonalait a forgó tárcsa metszi. Ennek következtében a tárcsában örvényáram indukálódik, amely a Lenz-törvény értelmében fékezi a tárcsa mozgását. A fékező forgatónyomaték arányos a tárcsa szögsebességével, továbbá az arányossági tényező (és így a csillapodást létrehozó nyomaték) az áram erősségével szabályozható. A spirálrugó által létrehozott kitéréssel arányos visszatérítő forgatónyomaték, és az örvényáramok miatti szögsebességgel arányos fékező forgatónyomaték együttesen exponenciálisan csillapodó forgási rezgést hoz létre. Ennek az exponenciális csillapodásnak köszönhető a maximális kitérések mértani sorozat szerinti csökkenése.
Kísérlet: A Pohl-féle készüléken a tekercsén átfolyó áram erősségének 0,2 A-re való beállításával mérsékelt csillapító hatást állítunk be, valamint a villanymotor kapcsaira elektromos feszültséget kapacsolva a motor a feszültségtől függő fordulatszámmal forog. A filmen az áramerősséget a szürke, míg a kapocsfeszültséget a sárga műszer mutatja. Jól látható, hogy a motor forgásának következtében a spirálrugónak a fekete forgó rúdhoz rögzített vége rezgő mozgást végez. A kísérlet során a motor fordulatszámát változtatjuk, a csillapítást eredményező áram erősségét állandó értéken hagyjuk.
Megfigyelés: Bizonyos idő elteltével - a tranziens (vagy átmeneti) jelenségek elmúltával - a tárcsa a motor fordulatszámával pontosan megegyező harmonikus forgási rezgést végez. Figyeljük meg, hogy ha a motort lassan forgatjuk, akkor a tárcsa rezgése is lassú, míg ha gyorsan forgatjuk, akkor a rezgése is gyors. Érdekes, hogy a tárcsa nem a rá jellemző sajátfrekvenciájának megfelelő rezgésszámú rezgést végez, hanem a motor (illetve a vele azonos rezgésszámú rezgést végző fekete rúd) frekvenciájával rezeg. Vagyis a motor - a gerjesztő rendszer - rákényszeríti a rezgésszámát a tárcsára, a gerjesztett vagy kényszerített rendszerre. Ezért nevezik a kialakuló rezgést kényszerrezgésnek. A kialakult kényszerrezgés amplitúdója és fáziskésése a gerjesztéshez viszonyítva a gerjesztési frekvenciától függ. A gerjesztett rendszer sajátfrekvenciájánál sokkal kisebb gerjesztési frekvencia esetén a kényszerrezgés amplitúdója kicsi, míg a fázisa a gerjesztéssel azonos fázisú. Ekkor a filmen a fekete és a fehér csúcs azonos irányba mozog. Növelve a gerjesztés frekvenciáját az amplitúdó növekszik, a sajátfrekvenciánál eléri a maximumát. Ez a jelenség a rezonancia. Rezonancia esetén a kényszerrezgés negyed periódussal késik a gerjesztéshez képest. Tovább növelve a gerjesztés frekvenciáját, a kényszerrezgés amplitúdója ismét csökken. A rezonanciafrekvenciától távol a kényszerrezgés fázisa ellentétes a gerjesztés fázisával. Ekkor a kísérletben a fekete és a fehér csúcs ellentétesen mozog.
Magyarázat: A villanymotor forgatásával a fekete rudat és vele együtt a hozzárögzített spirálrugót harmonikus forgási rezgésbe hozzuk, Ennek következtében a spirálrúgó a tárcsára a motor fordulatszámával azonos frekvenciájú harmonikusan rezgő forgatónyomatékkal hat, amely gerjesztő hatásként, a kitéréssel arányos visszatérítő, valamint a szögsebességgel arányos fékező forgatónyomatékokkal együttesen - a csillapodó rezgéssel kapcsolatos átmeneti jelenségek elmúltával - a gerjesztéssel megegyező harmonikus forgási rezgésre, úgy nevezett kényszerített rezgésre készteti a tárcsát. A kényszerrezgés amplitúdója a gerjesztés frekvenciájától függ. A sajátfrekvenciánál sokkal kisebb, vagy sokkal nagyobb gerjesztési frekvenciáknál az amplitúdó kicsi. Kicsi csillapítás esetén az amplitúdó a sajátfrekvenciával megegyező gerjesztési frekvencián éri el a maximumát, ez a rezonancia esete. Rezonancia esetén igen kicsi gerjesztő hatások is igen nagy amplitúdójú rezgéseket képesek létrehozni! Ezt az épültek tervezésénél nem árt figyelembe venni. A nem megfelelő tervezés katasztrófához is vezethet! Jó példa erre az Egyesült Államokban lévő Tacoma folyón átívelő híd leszakadása 1940. nov. 7-én.
Kísérlet:A Pohl-féle készülék tárcsájára - a fehér nyílhoz - egy kis póttömeget erősítünk. Ezzel egy olyan mechanikai rendszerhez jutunk, melyen az anharmonikus rezgések és a rezgések kialakulásának feltételei jól szemléltethetők. A kísérletben látható, hogy a rendszer két stabil és egy instabil egyensúlyi helyzettel rendelkezik. Kezdősebesség nélkül a stabil egyensúlyi helyzetbe helyezve a rendszert, a rendszer egyensúlyban marad. A tárcsa balra illetve jobbra való elforgatásával két ilyen helyzetet találhatunk. A stabil egyensúlyi helyzetből kicsit kitérítve a tárcsát az egyensúlyi helyzet körüli periodikus mozgás, azaz rezgés alakul ki. Az instabil egyensúlyi helyzet a két stabil egyensúlyi helyzet között középen található. Innen kicsit kitérítve a tárcsát (kicsiny zavaró hatásra) a tárcsa eltávolodik az egyensúlyi helyzetétől.

1.7.2. ábra Nehezékkel ellátott Pohl-féle készülék anharmonikus rezgések szemléltetésére. Bal és jobb oldalon a két stabil egyensúlyi helyzet látható.
Megfigyelés: Figyeljük meg és jegyezzük meg a stabil egyensúlyi helyzetet megadó számokat a tárcsa melletti skálán! Az egyensúlyi helyzet közelében történő (azaz kis amplitúdójú) rezgések közel harmonikusak, míg az anharmonikus jelleg annál szembeötlőbb, minél inkább eltávolodik a rendszer az egyensúlyi helyzettől. A kialakuló rezgés tartománya kezdeti feltételektől (kezdeti szögelfordulástól és szögsebességtől) függ. Elegendően távolról (elegendően nagy kezdeti energiával) indítva a rendszert olyan rezgés alakul ki, amely magába foglalja mind a három egyensúlyi helyzetet. Ekkor a rezgés anharmonikus volta igen szembeötlő. A tengelynél fellépő kicsi súrlódás miatt a rezgés csillapodik. Egy idő után a rendszer nem jut át az instabil egyensúlyi helyzetnél (középen) lévő potenciál hegyen, ezután az egyik stabil egyensúlyi helyzet körül kezd (csillapodó) rezgést végezni.
Magyarázat: A Pohl-féle készülék tárcsájára egy kis póttömeget erősítve, két stabil és egy instabil egyensúlyi helyzettel rendelkező mechanikai rendszert kapunk. A stabil egyensúlyi helyzetek ott találhatók, ahol a póttömeg súlyából származó forgatónyomaték megegyezik a tárcsa elfordulásával a spirál rugó által létrehozott forgatónyomatékkal. Ismeretes, hogy rezgések a stabil egyensúlyi helyzetek körül alakulhatnak ki, hiszen ekkor a tárcsára ható nyomaték az egyensúlyi helyzetbe igyekszik visszaforgatni a tárcsát.
Jól ismert egy tömegpont egyenes vonalú mozgása és egy rögzített tengely körül forgó merev test forgó mozgása közti analógia. A kísérletünk tömegpontra vonatkozó megfelelője - a mechanika egy fontos problémája - a potenciálgödörben mozgó részecske mozgása. A következő három animáció egy olyan esetet szemléltet, amikor a részecske helyzeti energiájának két (lokális) minimuma és egy lokális maximuma van a két minimum között. A filmeken felül láthatjuk a részecske helyzetét az idő függvényében, míg alul a helyzeti energiát a helyzet függvényében. A helyzeti energia minimumhelyeinél találjuk a stabil egyensúlyi helyzeteket, míg a maximumhelynél instabil egyensúlyi helyzet van. Rezgések a stabil egyensúlyi helyzet körül alakulnak ki. A kialakult (anharmonikus) rezgés tartományát a kezdeti feltételek által meghatározott (a kék vízszintes vonallal jelölt) teljes mechanikai energia jelöli ki. A rezgés fordulópontjai (a zérus sebességű pontok) ott lesznek, ahol a potenciális energia egyenlő a teljes energiával, ugyanis itt a mozgási energia (és így a sebesség is) zérus. Amennyiben a teljes energia kisebb, mint a közbülső potenciálhegy magassága, akkor csak az egyik (a kezdeti feltételektől függően a bal vagy a jobb oldali) stabil egyensúlyi helyzet körül alakul ki rezgés. Azonban, ha a teljes energia nagyobb, mint a potenciálhegy magassága, akkor a rezgés tartománya tartalmazza mindkét stabil egyensúlyi helyzetet.
Kísérlet:Egy nagy tömegű és öt sokkal kisebb tömegű, különböző hosszúságú ingát egy közös kifeszített fonálra erősítünk, majd a nagy tömegű ingát kitérítve elengedjük. A gerjesztő rezgés az adott hosszúságú, nagy tömegű inga lengése. A kényszerített rezgő rendszer az öt különböző hosszúságú inga, melyek hosszát úgy választottuk meg, hogy a középső inga hossza megegyezik a gerjesztő inga hosszával, míg két inga rövidebb, kettő pedig hosszabb.

1.7.3. ábra Kényszerrezgést ingákkal szemléltető elrendezés
Megfigyelés: Figyeljük meg, hogy az ingák nem a rájuk jellemző sajátfrekvenciával, hanem a gerjesztési (azaz a nagy tömegű inga rezgésének megfelelő) frekvenciával végeznek rezgő mozgást. A rezonancia (a legnagyobb amplitúdójú rezgés) annál az ingánál figyelhető meg, amelynek a sajátfrekvenciája (hossza) megegyezik a gerjesztési frekvenciájával (gerjesztő inga hosszával). Az is jól látható, hogy rezonancia esetén a kényszerített rendszer negyed periódussal (π/2 fázissal) késik a gerjesztéshez képest.

1.7.4. ábra Rezonancia esetén a kényszerrezgés negyed periódussal késik a gerjesztéshez képest
Magyarázat: Az ingák egy közös kifeszített fonálra vannak felerősítve, amely a nagy tömegű gerjesztő ingát lengésbe hozva, a gerjesztő ingával együtt mozog. Így az öt kis tömegű inga felfüggesztése a gerjesztő ingával együtt rezgő mozgásba jön, amely egy harmonikusan változó gerjesztő erőként jelenik meg a kis tömegű ingák mozgásánál. A gerjesztő rendszer tömegét azért kell nagynak választani, hogy a többi inga mozgása ne befolyásolja jelentősen a gerjesztést. Ellenkező esetben nem kényszer-, hanem csatolt rezgéssel lenne dolgunk.
Kísérlet: Hullámkádban egy egyenes lemez rezgetésével egyenes hullámfrontú vízhullámot keltünk és a hullám útjába egy egyenes - a vízből kiálló, a hullámhossznál jóval nagyobb méretű - alumínium lemezt teszünk. A hullám terjedési iránya és a visszaverő lemezre merőleges egyenes (a beesési merőleges) által bezárt szöget, a beesési szöget (a nulla foknak megfelelő) merőleges beeséstől a lemez forgatásával növeljük.
Megfigyelés: Figyeljük meg, hogy a visszavert hullám terjedési iránya és a beesési merőleges által bezárt szög, a visszaverődési szög változik a beesési szög változtatásával. A pontos vizsgálat azt mutatja, hogy ez a két szög egyenlő egymással. Jól látható, hogy hosszabb hullámvonulatok esetén a beeső és a visszavert hullám találkozik egymással. Ez hozza létre a kísérletben látható rácsozott mintázatot. Ez a jelenség már a hullámok interferenciájával kapcsolatos.
Magyarázat: A hullámok visszaverődése a Huygens-féle elvvel magyarázható, amely szerint a tér egy adott pontja egy elemi gömbhullám kiinduló pontjává válik abban az időpontban amikor a beeső hullámfront eléri a pontot. Egy későbbi időpontban megfigyelhető hullámfelületet az elemi hullámok hullámfelületeinek a burkoló felülete adja meg. Ennek megfelelően a visszaverő felület pontjai elemi körhullámokat sugároznak ki, amikor a beeső hullámfront eléri őket. Megmutatható, hogy az elemi hullámok burkolója egy olyan egyenes hullámfrontú hullámot eredményez, melyre a visszaverődés szöge egyenlő a beesés szögével. A két szög a beesési merőleges átellenes oldalán van.

1.8.1. ábra A visszaverődés szemléltetése. Kék vonal a beesési merőlegest, piros vonal a hullámok terjedési irányát mutatja. A beesési szög α, a visszaverődési szög β. A kísérletekből azt a következtetést vonhatjuk le, hogy a visszaverődési szög egyenlő a beesési szöggel (β = α).
Kísérlet : Hullámkádban egy kispálcával körhullámot keltünk, és a hullám útjába a hullámhossznál jóval nagyobb méretű, a vízből kiálló egyenes alumínium lemezt teszünk. A lemezről a beeső körhullám visszaverődik, és a visszavert hullám szintén körhullám.
Megfigyelés: Figyeljük meg, hogy a visszavert hullámfront megegyezik egy olyan körhullámnak a frontjával, melynek a forrása a lemez mögött, a beeső hullám forrásának a geometriai tükörképében van.
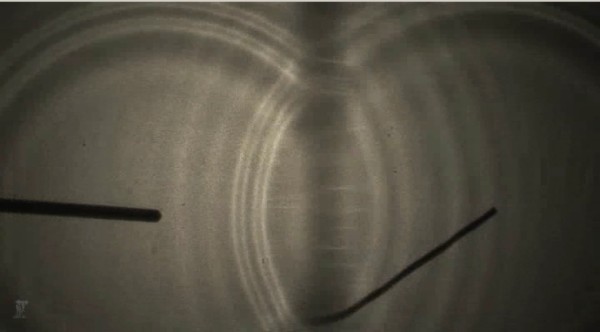
1.8.2. ábra A visszaverő felület mindkét oldalán egyszerre indítunk egy körhullámot. A kép már a visszaverődés utáni helyzetet mutatja. Ez a kísérlet az szemlélteti, hogy egy pontszerű forrásból kiinduló hullám síkfelületről úgy verődik vissza, mintha a forrás geometriai tükörképéből indult volna ki.
Magyarázat: A jelenség szintén a Huygens-féle elvvel értelmezhető. Ez a kísérlet segít megérteni az optikai síktükör képalkotását. A tükör előtti tárgy mindenegyes pontjából gömbhullámok indulnak ki, majd a tükörről úgy verődnek vissza, mintha a pont geometriai tükörképéből indultak volna ki. A látás szempontjából csak a szemünkbe jutó hullámnak (esetünkben a visszavert hullámnak) közvetlenül a szemünk előtti frontja számít, függetlenül attól, hogy az egy visszavert hullámból vagy egy valóban a tükör mögött lévő forrásból származik-e.
Kísérlet : Kör alakúra hajlított, a vízből kiálló alumínium lemezre egyenes hullámot ejtünk.
Megfigyelés: A hullám a lemezről visszaverődve egy adott pont (a fókuszpont) felé tartó körhullámmá alakul át. A kísérlet megfordítható, vagyis ha a fókuszban keltünk egy körhullámot, akkor az a körfelületről visszaverődve egyenes hullámmá alakul át.
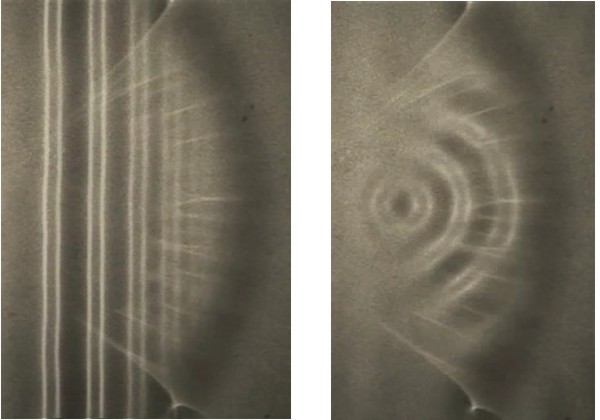
1.8.3. ábra Kör alakú akadályra beeső hullám közvetlenül az akadály előtt (bal oldali kép), majd a visszaverődés után (jobb oldali kép).
Magyarázat: A jelenség az előző kísérletekben megismert visszaverődés törvényének segítségével magyarázható. Teljesen hasonlóan elven gyűjti össze a fényt a fókuszpontjába egy homorú tükör, csak fény esetén a hullámfrontokat közvetlenül nem látjuk. Ugyancsak ezt a fókuszáló hatást használják fel a műholdról sugárzott TV adások vételére használatos parabola antennák. A fordított jelenségen (vagyis a fókuszból indított hullám visszaverődésén) alapul például az autók reflektorának működése.
Kísérlet : Kör alakúra hajlított, a vízből kiálló alumínium lemezre kör hullámot ejtünk.
Megfigyelés: A hullám a lemezről visszaverődve egy adott pont (a képpont) felé tartó körhullámmá alakul át. Ha a forrás (tárgypont) a kör alakú lemez görbületi középpontján kívülről indul, akkor a képpont a görbületi középpont és fókuszpont között található. Minél távolabb van a forrás a lemeztől, annál közelebb van a képpont a fókuszhoz. Az előző kísérletbeli beeső egyenes hullám olyan határesetnek tekinthető mikor a forrás nagyon messze van a lemeztől. Ha a forrást a görbületi középpont és fókuszpont között van, akkor visszaverődés után a hullámok a görbületi középponton kívül gyűlnek össze. Ha forrást a fókuszon belülre tesszük, akkor a lemezről egy olyan körhullám verődik vissza, amely mintha a lemez mögötti pontból indult volna ki.

1.8.4. ábra Kör alakú akadályra beeső a görbületi középponton kívüli pontból induló körhullám a visszaverődés előtt (bal oldali kép), majd a visszaverődés után (jobb oldali kép).
Magyarázat: A jelenség az előző kísérletekben megismert visszaverődés törvényének segítségével magyarázható. Ugyanez a jelenség játszódik le a gömbtükrök képalkotásánál fény esetén. A fényhullám (közvetlenül nem megfigyelhető) hullámfelülete teljesen hasonlóan változik meg a visszaverődés során.
Kísérlet : Ellipszis alakúra hajlított, a vízből kiálló alumínium lemezre kör hullámot ejtünk úgy, hogy a hullámok kiindulási pontja (a forrás) az ellipszisen belül van. A kísérlet során a forrás helyét változtatjuk.
Megfigyelés: Ha a hullámot az ellipszis egyik fókuszpontjából indítjuk, akkor a visszavert hullám a másik fókuszpont felé tartó körhullám lesz. Más pontokból kiinduló hullámra ez az állítás nem igaz.

1.8.5. ábra Az ellipszis baloldali fókuszából kiinduló hullámból (bal oldali kép) a visszaverődés után a másik fókusz felé tartó körhullám lesz (jobb oldali kép). A piros vonal az ellipszis egy adott pontjához tartozó beeső és visszavert hullámok terjedési irányait, a kék vonal az adott ponthoz tartozó beesési merőlegest mutatja. Az ellipszis geometriai tulajdonsága miatt a beesési merőleges a terjedési irányokkal pontosan azonos szöget zár be. Ez pedig pontosan azt jelenti, hogy a baloldali fókuszból érkező hullámfront a visszaverődés után a jobboldali fókuszpont irányába verődik vissza!
Magyarázat: A jelenség a visszaverődés törvényével és a kúpszeletek geometriai tulajdonságával magyarázható. A fókuszból induló körhullám frontja a forrástól az ellipszis másik fókuszpontjáig - az ellipszis geometriai tulajdonsága miatt - minden irányba pontosan ugyanakkora utat tesz meg. Ennek a ténynek az a következménye, hogy a visszavert hullám frontja egy adott pillanatban minden irányban pontosan azonos távolságra van a másik fókusztól, ez pedig pontosan azt jelenti, hogy a visszavert hullám egy olyan körhullám, amely frontjának a görbületi középpontja a másik fókuszpont.
Az ellipszis fontos geometriai tulajdonsága, hogy egy tetszőleges pontjából a két fókuszba húzott szakaszokból kapott szöget (a jobb oldali képen 2α) a pontba állított ellipszisre merőleges egyenes (itt a beesési merőleges) éppen felezi. Az egyik félszög (α) a beesési szög, a másik félszög pedig a visszaverődési szög. Mivel ez a szög szintén α, így a baloldali fókuszból kiinduló sugár úgy verődik vissza, hogy a visszavert sugár a másik fókuszon megy keresztül, amely éppen azt jelenti, hogy az egyik fókuszból érkező hullámfront a visszaverődés után a másik fókuszpont irányába verődik vissza.
Kísérlet: Hullámkádba üveglemezt helyezünk, ezzel a kádban különböző vízmélységű tartományokat állítunk elő. Egyenes lemez rezgetésével olyan egyenes hullámokat keltünk, melyek a különböző mélységű területek határa felé tartanak először úgy, hogy a hullámok a mélyebb tartományból lépnek a sekélyebb tartományba, majd amikor a sekélyebb tartományból haladnak a mélyebb tartomány fele.
Megfigyelés: Figyeljük meg, hogy ferde beesés esetén a határon áthaladva a hullámok terjedési iránya megváltozik, ez a jelenség a hullámok törése. Vegyük észre, hogy a terjedési irányon kívül még a hullámhossz is megváltozik. Merőleges beesés esetén a terjedési irány nem változik meg (azaz nincs törés), azonban a hullámhossz a ferde beesésnek megfelelően változik!

1.8.6. ábra Vízhullámok törése ferde (bal oldali kép) és merőleges beesés esetén (jobb oldali kép). A hullámok a mélyebb tartományból lépnek a sekélyebb tartományba. Piros vonal a hullám terjedési irányát, a kék vonal a beesési merőlegest mutatja. A képen jól látható a sekélyebb tartományon a kisebb terjedési sebességből eredő hullámhosszrövidülés.
Az 1.8.6. és az 1.8.7. ábrákon jól látható, hogy ha a hullámok a mélyebb részből haladnak a sekélyebb felé (c1 > c2), akkor a törési szög (α2) kisebb, mint a beesési szög (α1). Ha viszont a sekélyebb részből haladnak a mélyebb fele (c1 < c2) a hullámok, akkor a törési szög (α2) nagyobb, mint a beesési szög (α1). Ez utóbbi esetben, ha a beesési szög meghaladja a sin α h = c1/c2 képlettel meghatározott α h határszöget, akkor nincs megtört hullám. Ez a jelenség a teljes visszaverődés. A határszöghöz tartozik éppen a 90º-os törési szög. Ha a kísérlet során a vízmélységet csökkentjük, akkor a jelenséget meghatározó terjedési sebességek hányadosa változik, ennek megfelelően változik a határszög is. Az 1.8.7. ábrán látható esetekben a vízmélységet úgy állítottuk be, hogy (balról jobbra haladva) a beesési szög kisebb, közel azonos és nagyobb legyen, mint a határszög.
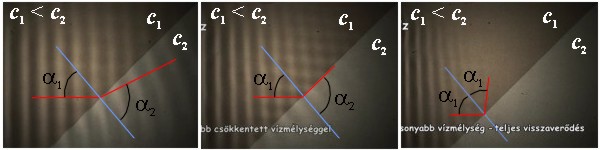
1.8.7. ábra Vízhullámok törése sekélyebb tartományból mélyebb tartomány felé terjedés során. Piros vonal a hullám terjedési irányát, a kék vonal a beesési merőlegest mutatja. Balról jobbra haladva az α1 beesési szög változatlan, míg a vízmélység fokozatosan csökken, csökkentve ezzel a α h = arcsin c1/c2 határszöget.
Teljes visszaverődés esetén valójában behatol a hullám a nagyobb terjedési sebességű tartományba, csak a hullám amplitúdója a határfelülettől távolodva igen kis távolságon belül exponenciálisan lecsökken, így a behatoló hullámot nem látjuk. Ez az exponenciálisan lecsillapodó hullám az evaneszcens hullám. Az evaneszcens hullám jelenlétét egy keskeny csatorna segítségével mutathatjuk ki (1.8.8. ábra). A vízmélységet úgy állítottuk be, hogy a teljes visszaverődés lépjen fel a csatorna határánál. Ekkor az üveglemezek felett a víz csupán néhány milliméter mély, melyben a vízhullámok amplitúdója gyorsan csillapodik a terjedés során. Így a visszavert hullám nehezen látható. Azonban ha jól megfigyeljük, a baloldali képen egy rácsozódó mintázatot lehet észrevenni, ami a visszavert hullámra utal. Mivel az evaneszcens hullám amplitúdója exponenciálisan csillapodik, a csatorna szélességét elegendően szélesre választva a hullámok nem haladnak át a csatornán. Azonban, ha a csatorna szélességét úgy lecsökkentjük, hogy ezen a távolságon belül a csillapodás ne legyen számottevő, akkor a hullámok már - a tejes visszaverődés feltételének fennállta ellenére - áthatolnak a csatornán, és a másik határfelületen az evaneszcens hullám már normál hullámként folytatja az útját, ahogy ezt a jobb oldali képen láthatjuk. Ez a kísérlet a klasszikus hullámtani megfelelője a kvantummechanikai alagút effektusnak.
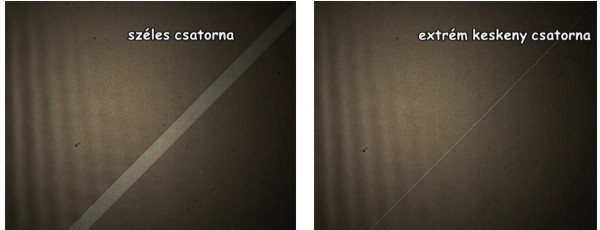
1.8.8. ábra Teljes visszaverődéskor fellépő exponenciálisan csillapodó hullám, az evaneszcens hullám kimutatása keskeny csatorna segítségével.
Magyarázat: Vízhullámok terjedési sebessége sekély vízmélység (cm-es nagyságrend) esetén függ mélységtől, még pedig úgy, hogy a mélyebb vízben gyorsabban terjednek a hullámok. Ennek megfelelően az üveglemez behelyezésével olyan tartományokat állítunk elő, ahol a hullámok terjedési sebessége különböző, nevezetesen az üveglemez felett lassabban terjednek a hullámok.
Ismeretes, hogy ha egy hullám egy olyan határfelülethez érkezik, ahol a terjedési sebesség megváltozik, akkor a felületen való áthaladáskor a hullám hullámhossza a terjedési sebességgel arányosan megváltozik, és a merőleges beeséstől eltekintve, a hullám terjedési iránya is megváltozik. Ez a jelenség hullámok törése, melyet az optikából jól ismert Snellius-Descartes-féle törvény ír le: sin α1 / sin α2 = c1/c2 = λ1/ λ2, ahol α1 és α2 a terjedési irányoknak a beesési merőlegessel bezárt szöge (beesési és törési szögek), c1 és c2 a terjedési sebességek, valamint λ1 és λ2 a hullámhosszak a határfelület két oldalán. Az n21 = c1/c2 hányadost a 2 közeg 1 közegre vonatkozó relatív törésmutatójának szokás nevezni. A jelenség a Huygens-elvvel értelmezhető.
A vízhullámok terjedési sebessége függ a hullám frekvenciájától, így a jelenség lefutása, vagyis a hullámhossz és a terjedési irány változása is függ a frekvenciától, ahogy ezt kísérletekben is láthatjuk.
Kísérlet: Hullámkádba lencse alakú (azaz mindkét oldalról körrel határolt) üveglemezt helyezünk. Ezzel az előző kísérlethez hasonlóan olyan tartományokat állítunk elő, ahol a hullámok terjedési sebessége különböző, csak itt a tartományokat szétválasztó határ görbült. Az üveglemez felett a vízmélység kisebb, ezért itt a hullámok lassabban terjednek. Először a beeső egyenes hullám útjába kétszer domború, majd utána kétszer homorú üveglemezt helyezünk.
Megfigyelés: Figyeljük meg, hogy a beeső egyenes hullám a bal oldali görbült felületen való áthaladáskor a törés miatt körhullámmá alakul át, majd a jobb oldali görbült határfelületen való törés miatt a körhullám frontjának görbületi sugara megváltozik, a hullámfrontok görbültebbek lesznek. Jól látható, hogy az üveglemez felett, ahol a hullámok lassabban terjednek, a hullámhossz is kisebb. Az 1.8.9. ábra bal oldalán látható esetben a kétszer domború lencsét egy a fókuszpont felé tartó, konvergens körhullám hagyja el, míg a jobb oldali példánál a kétszer homorú lencsét egy olyan körhullám hagyja el, amelynek frontjainak görbületi középpontja a lencse előtt van. Ez a pont a lencse virtuális fókuszpontja, és ekkor a körhullám divergens.
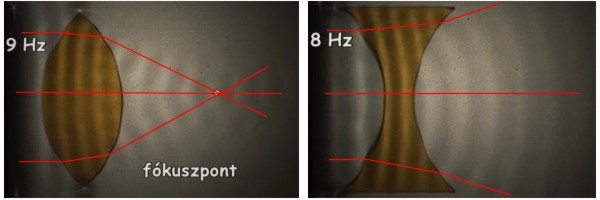
1.8.9. ábra Vízhullámok áthaladása gyűjtő- és szórólencsén. A lencse alakú üveglemez felett sekélyebb a víz, így ott a vízhullámok lassabban terjednek. Ezért a lencsék görbült felületénél bekövetkező törés miatt megváltozik a hullámterjedési iránya, melynek következtében a beeső egyenes hullám körhullámmá alakul át. A piros vonalak lencse felületének bizonyos pontjainál mutatják a hullám terjedési irányát.
Magyarázat: A jelenség a törést leíró Snellius-Descartes-féle törvénnyel értelmezhető. A görbült törő határfelület miatt a törés után a hullámfrontok is görbültek lesznek. Fény esetén a gömbi üveglencsék teljesen hasonló módon változtatják meg a fényhullám hullámfrontját. A lencse fókuszpontjának a helyét a törésmutató és a határfelületek görbületi sugara határozza meg, és a fókusztávolság is az optikából jól ismert 1/f = (n - 1) (1/R1 + 1/R2) lencseegyenletből számítható ki, ahol n a határfelületre vonatkozó (relatív) törésmutató és a R1 és R2 a határfelületek görbületi sugarai.
Kísérlet: Két azonos fázisban rezgő csúccsal két körhullámot keltünk. A kísérlet során változtatjuk a csúcsok frekvenciáját, ezzel változik a kialakuló hullámok hullámhossza. A filmen feltűnő, hogy bizonyos esetben a hullámok visszafelé haladnak, ez az úgy nevezett stroboszkópikus hatásnak köszönhető. A jelenséget a kamera okozza, mivel a képkockákat egy bizonyos frekvenciával (25 Hz) készíti, így úgy működik, mint egy stroboszkóp, amely egy bizonyos frekvenciával felvillanó lámpa.
Teljesen hasonló jelenséget kapunk akkor is, ha egyenes hullám útjába két keskeny nyílást tartalmazó lemezt helyezünk és a hullámok merőlegesen esnek be a lemezre. A kísérlet során a nyílásokat, külön - külön és együttesen is, lezárjuk majd kinyitjuk, valamint a hullámforrás frekvenciájának változtatásával a hullámhosszat is változtatjuk.
Megfigyelés: A kísérletek során a két hullám találkozása miatt jellegzetes mintázat alakul ki a vízfelszínen (1.8.10. ábra). Vannak olyan helyek ahol - annak ellenére, hogy hullámok érik el - nem figyelhető meg rezgés, míg vannak olyan helyek ahol sokkal nagyobb amplitúdójú rezgés alakul ki, mint a két találkozó hullám által (egyenként) keltett rezgések amplitúdóinak összege. Ezek az úgynevezett maximális gyengítési és maximális erősítési helyek olyan hiperbolákon helyezkednek el, melyek fókuszpontjai a két találkozó körhullám forrása.

1.8.10. ábra Két azonos hullámforrás által keltett körhullámok találkozásánál kialakuló jelenség. Bal oldalt a hullámforrás két azonos fázisban rezgő csúcs, míg jobb oldalt egyenes hullám útjába helyezett két keskeny nyílás.
Ha a kétréses kísérletnél valamelyik nyílást lezárjuk, akkor jól látható, hogy a másik keskeny nyílás valóban egy körhullám forrása (1.8.11. ábra).

1.8.11. ábra A kétréses kísérletnél az egyik nyílás lezárásával a másik nyílásból kiinduló körhullám megjeleníthető.
Magyarázat: A kísérletek során megfigyelt jelenség az interferencia, amely a hullámok találkozásánál tapasztalható, és a szuperpozíció elvével értelmezhető. A szuperpozíció elve szerint a találkozó hullámok egymás hatását nem befolyásolják, a megfigyelhető kitérés a két hullámhoz tartozó kitérések összege lesz. Ez alapján a maximális erősítési, illetve maximális gyengítési helyek ott vannak, ahol a két hullám azonos, illetve ellentétes fázisban találkozik. A fázisok viszonyát pedig a hullámok útkülönbsége határozza meg. Azokon a helyeken ahol az útkülönbség állandó, a fázisviszonyok is ugyanazok. Ezért találhatók a maximális erősítési és gyengítési helyek hiperbolákon, hiszen a hiperbola pontosan olyan pontok halmaza melyeknek a fókuszpontokról mért távolságaiknak a különbsége állandó.
Az interferencia egy fizikai jelenség hullámtermészetének fontos kísérleti bizonyítéka. Fény esetében nem mindig egyszerű az interferencia kimutatása. Ennek oka a fényforrások által kisugárzott elemi fény-hullámvonulatok véges (és igen rövid) hossza, másrészt az egyes elemi hullámvonulatok fázisának rendezetlen volta. A hullámvonulatok rövid hosszúságának hatását vízhullámokkal is könnyen szemléltethetjük. Ha olyan hullámot keltünk, amelynek a hossza rövid, mindössze néhányszorosa a hullámhossznak, akkor nem mindenhol figyelhetünk meg interferenciát. Azokon a helyeken, ahol az útkülönbség nagyobb, mint a hullámvonulatok hossza, a hullámok nem találkoznak, mert az egyik az adott helyen már áthaladt, mire a másik odaérkezik. Az ilyen helyeken nyílván nem figyelhető meg interferencia, hiszen ehhez a hullámok találkozása szükséges. Az 1.8.12. ábrán a jobb oldalon a hullámvonulatok hossza a hullámhossz háromszorosa. A két csúcsot összekötő egyenesre merőleges szimmetria tengelyen az útkülönbség zérus. Így itt a hullámvonulatok mindig találkoznak, még pedig azonos fázisban, amely maximális erősítést eredményez. A szimmetria tengelytől felfele illetve lefele távolodva, az útkülönbség növekszik, és a hullámhossz felét elérve maximális gyengítési helyhez érkezünk, mivel ez éppen ellentétes fázisú találkozást jelent. Tovább távolodva a tengelytől az útkülönbség tovább növekszik, hullámhossznyi útkülönbség ismét maximális erősítést eredményez. Ekkor viszont már a három hullámhossznyi hosszúságú hullámvonulatok részben lecsúsznak egymásról, már csak két hullámhossznyi részük fedi át egymást. Így az erősítés is gyengébb, mint a zérus útkülönbséghez tartozó központi erősítési hely. Fény esetében ez egy gyengébb világos interferencia csíkot jelent.

1.8.12. ábra Interferencia sok hullámhossznyi és háromhullámnyi hosszúságú hullámvonulatok esetén
Tovább távolodva a zérus útkülönbségnek megfelelő szimmetria tengelytől, a maximális erősítési és gyengítési helyek váltakoznak, azonban a hullámvonulatok egyre kevésbé fedik át egymást, így az erősítés, illetve a gyengítés egyre inkább csökken. Amint az útkülönbség meghaladja a hullámvonulatok hosszát, a vonulatok már nem találkoznak, így az erősítés és gyengítés, vagyis az interferencia megszűnik. Az elmondottak alapján már érhető, hogy a zérus útkülönbségnek megfelelő szimmetriatengelytől felfelé és lefelé annyi maximális erősítési illetve gyengítési hely van (egyre gyengülő hatással), ahányszor a hullámhossz ráfér a hullámvonulat hosszára. Fény estében a központi világos interferenciacsíktól szimmetrikusan, egyre csökkenő láthatósággal annyi világos és sötét csíkot figyelhetünk meg, ahányszor az elemi fényhullámvonulatok hosszára ráfér a fény hullámhossza.
Kísérlet: Hullámkádban egyenes hullámokat keltünk. A hullámok útjába a hullámhosszhoz viszonyított különböző méretű akadályokat, például hullámok terjedését a kád egyik felében gátoló lemezt (élt), vagy a hullámokat átengedő nyílást tartalmazó lemezt (rést), vagy a hullámok terjedését akadályozó lemezt teszünk (átlátszatlan akadály).
Megfigyelés: Mindennapos tapasztalat, hogy a hullámok - hasonlóan a fényhez - egyenes vonalban terjednek. Az előbbi kísérletek azonban éppen azt mutatják, hogy ez nem mindig teljesül. Ahogy az 1.8.13. ábrán és a filmeken is látható, amennyiben a hullámtérbe helyezett akadály mérete kezdi megközelíteni a hullámhossz nagyságrendjét, az egyenes vonalú terjedéstől jelentős eltérések mutatkoznak, ami azt jelenti, hogy a hullám olyan térrészbe is behatol, ahova az egyenes vonalú terjedés alapján nem jutna el (optikai analógia alapján árnyéknak nevezzük ezt a tartományt). Ez az egyenes vonalú terjedéstől való eltérés az elhajlás, vagy idegen szóval a diffrakció jelensége.

1.8.13. ábra Vízhullámok áthaladása d szélességű nyíláson (résen). A két piros vonal közötti tartomány az, ahova a hullámok az egyenes vonalú terjedés alapján eljuthatnak, míg a felső vonal feletti és az alsó vonal alatti tartomány az egyenes vonalú terjedés alapján tiltott rész, az árnyék tartomány. Látható, hogy az elhajlás mértéke, vagyis az egyenes vonalú terjedéstől való eltérés, a nyílás szélességének és a hullámhossznak viszonyától függ.
Az elhajlás mértékét a rés szélességének és hullámhossznak a viszonya határozza meg: minél inkább megközelíti a rés szélessége a hullámhosszat, annál jelentősebb az árnyéktérbe való behatolás. Az 1.8.14. ábrán látható, hogy ha a rés szélességét közel a felére csökkentjük, akkor változatlan hullámhossz mellett az elhajlás mértéke nagyobb, vagyis a hullámok jobban behatolnak az árnyék tartományba.

1.8.14. ábra Az elhajlás mértéke a rés szélességének és a hullámhossznak a viszonyától függ, változatlan hullámhossz mellett kisebb rés szélességre nagyobb az árnyéktérbe való behatolás.
Magyarázat: Az egyenes vonalú terjedéstől való eltérés, az elhajlás (diffrakció) a Huygens-féle elv tökéletesített változatával, a Huygens-Fresnel-féle elvvel magyarázható. Ezen elv szerint a hullámfelület minden egyes pontja elemi hullámforrásnak tekinthető, és a hullámtér egy adott pontjában megfigyelhető hullámjelenséget ezen elemi hullámok interferenciája határozza meg. Az akadály szerepe tulajdonképpen az, hogy a hullámfront bizonyos részét kivágja.
Ha a nyílás mérete a hullámhossz nagyságrendjébe esik, akkor a nyílástól viszonylag távol, akár az árnyéktérben fekvő megfigyelési pontnak a távolsága a nyílás pontjaitól gyakorlatilag azonos. Így az útkülönbségek az elemi hullámok között jóval a hullámhossz alatt vannak, ezért a nyílás pontjaiból kiinduló elemi hullámok azonos fázisban találkoznak, azaz erősítik egymást. Ennek megfelelően egy ilyen pontban nyílván hullámjelenséget figyelhetünk meg.
Az elmondottak alapján bizonyos résszélességeknél nyílván találhatunk olyan helyeket is, ahol az elemi hullámok úgy találkoznak, hogy nem erősítik, hanem gyengítik egymást. Ilyen eset látható az 1.8.15. ábrán.

1.8.15. ábra A nyílást kitöltő hullámfront pontjaiból kiinduló elemi hullámok bizonyos megfigyelési pontokban erősíthetik, vagy akár gyengíthetik is egymást a köztük lévő útkülönbségtől függően. Az ábrán piros vonal jelöli azokat a helyeket, ahol az elemi hullámok erősítik, míg kék vonal azokat a helyeket, ahol gyengítik egymást.
Kísérlet : Hullámkádban egyenes hullámokat keltünk és a hullámok útjába a hullámhossznál kisebb méretű akadályt helyezünk.
Megfigyelés: A kísérletben jól látható, hogy a hullámhossznál kisebb méretű akadályból, amint a beérkező hullámfront eléri az akadályt, körhullám indul ki. Vagyis a kisméretű akadály, az úgynevezett szóró centrum a beeső hullám hatására hullámforrássá válik, a belőle minden irányba kiinduló hullám a szórt hullám, a megfigyelt jelenség pedig a hullámok szórása. Ilyen szórást a fény esetében is megfigyelhetünk, ez adja például az égbolt kék színét.

1.8.16. ábra Ha a hullámok útjába a hullámhossznál kisebb méretű akadályt helyezünk, akkor az akadály a beeső hullámhatására hullámforrássá válik, az akadályból körhullám indul ki. Ez a jelenség a hullámok szórása.
Magyarázat: A jelenséget a Huygens-Fresnel-féle elv alapján értelmezhetjük: amikor a beeső hullámfront eléri a gyakorlatilag pontszerű akadályt, az adott pont elemi hullámforrásnak tekinthető. Az innen kiinduló elemi hullám a szórt hullám.
Kísérlet : Hullámkádban két azonos fázisban rezgő, egymástól adott távolságban lévő csúccsal két körhullámot hozunk létre, melyek egy kör alakúra hajlított lemezről (homorú tükörről) visszaverődnek. A kísérlet során a csúcsok távolságát csökkentjük.
Megfigyelés: Az egyetlen rezgő csúccsal végzet, hasonló kísérletnél láttuk, hogy a csúcsból kiinduló körhullám a homorú tükörről visszaverődve egy adott pont (a képpont) felé tartó konvergens körhullámmá alakul át. Ez a kísérlet a képalkotás hullámtani modelljét szemlélteti.
Mivel most két forrásunk van, ezért azt várjuk, hogy a homorú tükörről két konvergens körhullám tart a két forrásnak megfelelő képpontok felé, persze a két hullám interferenciája nehezíti a megfigyelésüket. Abban az időintervallumban amikor a két hullám áthalad a két képponton, a képpontok helye jól felismerhető a felvételen és az 1.8.17. és az 1.8.18. ábrákon. Figyeljük meg, hogy ha a két csúcsot egymáshoz egy bizonyos távolságnál közelebb helyezzük, akkor a két képpont egybeolvad!
Magyarázat: Az optikában fontos kérdés, hogy egy képalkotó eszköz (például távcső vagy mikroszkóp) mikor képes felbontani két tárgypontot. Belátható, hogy az elhajlás miatt egy pontszerű tárgy képe sohasem pontszerű, hanem egy kicsi korong, melynek a mérete a hullámhosszal és a fókusztávolsággal egyenesen, míg a képalkotó eszköz nyílásának sugarával fordítottan arányos. Ezért ha a két tárgy közel van egymáshoz a két képnek megfelelő korong összeolvad. Ez azt jelenti, hogy egy képalkotó eszköz nem képesek felbontani a tárgy tetszőleges finom részleteit, így csak bizonyos méretnél nagyobb szerkezeteket vagyunk képesek vele tanulmányozni.
A képalkotásra vonatkozó Abbe-féle elmélet szerint a képalkotó eszköz akkor oldja fel a két tárgypontot, továbbá a kialakuló kép a tárgyhoz hasonló, ha a képalkotó eszközön legalább három szomszédos interferencia rend áthalad. Ez a feltétel nagyon jól megfigyelhető a kísérletünknél. Az első esetben, mikor a két csúcs a legtávolabb van, a homorú tükörre öt szomszédos interferencia rend esik. A második esetben, amikor a csúcsokat közelebb helyeztük, még mindig három szomszédos interferencia rend - a 0, a +1 és a -1 rendek, esik a homorú tükörre. A filmen és az 1.8.17. ábrán jól látható, hogy ekkor a két képpont még jól elkülönül.

1.8.17. ábra Két egymástól adott távolságra lévő, azonos fázisban rezgő csúccsal keltett körhullámok visszaverődése homorú tükörről. A két csúcs távolságát úgy állítottuk be, hogy a tükörre három szomszédos, a 0, a +1 és a -1 interferencia rendek essenek. Bal oldalon a csúcsokat éppen elhagyó, középen a közvetlenül a tükröt elérő, míg a jobb oldalon a képpontokon éppen áthaladó, már visszavert hullámok láthatók.
A harmadik esetben a két csúcsot olyan közel helyeztük, hogy a homorú tükörre gyakorlatilag már csak a 0 rend essen. Ekkor már nem teljesül a felbontásra vonatkozó Abbe-féle feltétel. A filmen és az 1.8.18. ábrán jól látható, hogy már csak egyetlen képpont jön létre, azaz a homorú tükör nem oldotta fel a két közeli, de külön álló tárgypontot!

1.8.18. ábra A két csúcsot egymáshoz közelebb helyezve a tükörre már gyakorlatilag csak a 0 interferenciarend esik, ahogy azt a középső kép mutatja. A jobb oldali képen látható, hogy a visszavert hullám már csak egyetlen képpont hoz létre.
Kísérlet : Hullámkádban egyenes lemez impulzusszerű (rövid ideig tartó lökésszerű) rezgetésével rövid, egy-két hullámhegyből álló egyenes hullámot hozunk létre.
Megfigyelés: Figyeljük meg a rövid, kezdetben egy-két hullámhegyből álló hullámvonulat változását a terjedés során. Jól látható, hogy a hullámhegyek egymáshoz viszonyított távolsága változik a hullámvonulaton belül, a hullámvonulat elején közelebb vannak a hullámhegyek, míg a végén a köztük lévő távolság nagyobb. A felvételen látszik, hogy a hullámvonulat rövidebb periódusú részei gyorsabban terjednek, mint hosszabb periódusú rész.

1.8.19. ábra A baloldalon látható, kezdetben rövid hullámvonulat a terjedés során kiszélesedik, továbbá a hullámhegyek egymás közötti távolsága is változik a hullámvonulaton belül. A jobb felső sarokban lévő szám a filmkockának a számát mutatja, míg alul a baloldali képtől számított időt tüntettük fel.
Magyarázat: A látott jelenség oka a diszperzió, amely a vízhullámokon kívül sok más hullámnál is fellépő jelenség. Diszperzióról akkor beszélünk, amikor a (térben végtelen kiterjedésű) szinuszos hullámoknak a terjedési sebessége függ a hullámhosszuktól.
Ismert, hogy egy térben lokalizált hullámjelenséget - egy véges hosszúságú hullámvonulatot - egy adott hullámhossztartományba eső, különböző hullámhosszúságú szinuszos hullámok összegeként állíthatunk elő. A hullámhossz tartomány annál szélesebb, minél rövidebb a hullámvonulat. Amennyiben a szinuszos (más néven a monokromatikus) összetevők terjedési sebessége függ a hullámhosszuktól, azaz diszperzió lép fel, akkor az összetevők egymáshoz viszonyított helyzete változik a terjedés során. Ez pedig nyílván azt eredményezi, hogy az összegükként kapott eredő hullámjelenség tér- és időbeli tulajdonságai is változnak a terjedés során.
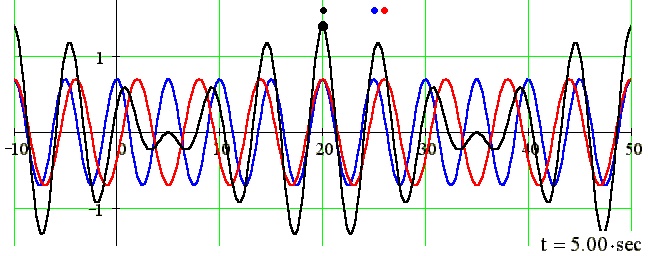
1.8.20. ábra Két különböző hullámhosszúságú szinuszos hullám (kék és piros vonalak) összegéből kialakuló hullám pillanatfelvétele (fekete vonal). A piros színnel rajzolt hullám hullámhossza nagyobb és az animációban ez terjed nagyobb sebességgel.
Az 1.8.20. ábrán és a hozzátartozó animáción egy olyan hullámjelenséget látunk, amely mindössze két különböző hullámhosszú szinuszos hullám összege, és a két összetevő terjedési sebessége különböző. Kezdetben az x = 0 helyen a piros és a kék színel rajzolt hullámnak két hullámhegye egybeesik, így az eredő, fekete színnel rajzolt hullámnak kezdetben az x = 0 helyen van a maximuma. A piros és a kék hullámnak az említett hullámhegyei fölé a nekik megfelelő színű pontot rajzoltunk. Látható, hogy a piros pont gyorsabban halad, vagyis a piros (nagyobb hullámhosszúságú) hullámnak a terjedési sebessége nagyobb, mint a kék hullámé. A fekete pont azt helyet jelöli, ahol az eredő hullám amplitúdója maximális. Ennek a maximális amplitúdójú helynek a terjedési sebességét nevezik csoportsebességnek. A szinuszos hullámok terjedési sebességét fázissebességnek is szokás nevezni, mert a hullámon belül a rezgés fázisa pontosan ekkora sebességgel terjed. Látható, hogy a csoportsebesség az animációban kisebb, mint a két összetevő hullámnak fázissebessége. A nagyobb méretű fekete pont az x = 20 helyen lévő pontnak az eredő hullámhoz tartozó rezgését mutatja.
Figyeljük meg, hogy az eredő hullámvonulaton belüli hullámhegyek fázissebességgel terjednek. Mivel ez az animációban nagyobb, mint a csoportsebesség, a hullámhegyek lehagyják a maximális amplitúdójú helyet. A maximális amplitúdójú hely felé közeledve a hullámhegy felerősödik, majd a lehagyva azt lecsillapodik.
A következő animáció egy kezdetben rövid, öt hullámhegyet tartalmazó hullámvonulatnak a terjedés során bekövetkező változását szemlélteti. A monokromatikus komponensek terjedési sebességét a vízhullámokra jellemző diszperziós összefüggéssel írtuk le, de a hullámok terjedése során bekövetkező csillapodást nem vettük figyelembe. Az animáció teljesen összhangban van a vízhullámokkal végzett kísérlettel: jól látható, hogy a rövidebb periódusú részek gyorsabban terjedek. A diszperzió hatására a kezdetben rövid hullámvonulat kiszélesedik.
Tartalom
- Kísérletek a fizikai fénytan témaköréből
- Fény-anyag kölcsönhatás
- A fény hullámtermészetű, kölcsönhatásra képes energiaáramlás
- Diszperzió (összetett és monokromatikus fény)
- Tyndall jelenség, a koherens fényszórás függése különböző paraméterektől
- A koherens fényszóródás típusai, fényszóródási jelenségek környezetünkben
- Színes oldatok, színszűrők fényelnyelése
- Környezetünk színei
A fényinterferencia két különböző fényforrással a fénykibocsátás atomi természete miatt nem hozható létre. Interferenciaképes, azaz koherens, azonos frekvenciájú, állandó vagy szabályszerűen változó fáziskülönbségű fényhullámokat úgy állíthatunk elő, hogy az egy fénykibocsátási aktusból származó fénynyalábot kettéosztjuk (hullámfront osztás). Ennek egyik lehetséges módja a Fresnel-féle kettős(bi)prizma használata. A biprizma törőszöge közel 180o, melynek törő élével párhuzamosan elhelyezett R résen átjutó monokromatikus fény az S1, S2 virtuális képpontokból (fényforrásokból) látszik kiindulni. (2.1.1. ábra). Ezek éppen ezért koherens fényforrásként viselkednek. A felfogó ernyőnek van egy olyan tartománya, melyet mind a két félprizmán áthaladó hullámfront elér. Ebben a tartományban várhatunk fényinterferenciát. Ez erősítés lesz, ha a találkozó hullámok fázisa azonos, azaz útkülönbségük: ΔZ = 2kλ/2, ahol k = 0, ±1, ±2, ..., és gyengítés (azonos amplitúdó esetén kioltás), ha a hullámok ellentétes fázisban találkoznak, azaz útkülönbségük ΔZ = (2k+1)λ/2, ahol k = 0, ±1, ±2, ....
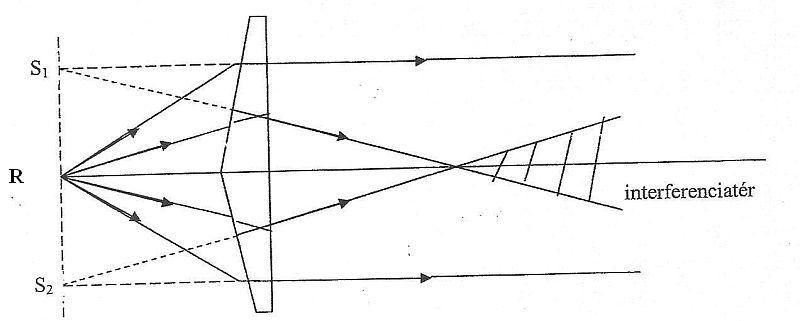
2.1.1 ábra (Forrás: Hadházy T., Nyilas I., Varga K.: Fizikai laboratóriumi gyakorlatok III., Bessenyei György Könyvkiadó, Nyíregyháza,2005, 43 old.)
További követelményt jelent, hogy az útkülönbség e feltételek teljesülése esetén sem lehet nagyobb az un. koherenciahossznál. Koherenciahossznak nevezzük annak a szakasznak a hosszát, amelyen belül a hullám egy része valamely más részével okvetlenül koherens. A koherenciahossz szoros kapcsolatban van a fény monokromatikus voltával, minél monokromatikusabb a fény, annál nagyobb a koherenciahossza. Lézer fényforrás esetében ez méter nagyságrendű, még izzólámpák esetében néhány tized milliméter. A fény tökéletesen monokromatikus (egyszínű), ha benne csak egyetlen hullámhossz fordul elő. Ebben az esetben a találkozó azonos frekvenciájú hullámok igen hosszú szakaszon mozognak tökéletes összhangban. Ez idealizált állapot, az összetevők általában egy Δλ intervallumba esnek. Így a Δλ értékétől függően (amely a monokromatikusság fokát jellemzi) hosszabb (kis Δλ) vagy rövidebb (nagyobb Δλ) szakaszú együttfutás után bomlik meg a találkozó hullámok összhangja.
Kísérlet : A kísérleti elrendezés fényforrásaként pontfényizzót használunk, melynek fényét az R résre ejtjük. (R~0,1-0,2 mm) A fényforrásból kiinduló, kis sávszélességű színszűrővel leszűrőzött fény a biprizmán áthaladva (2.1.1. ábra) interferál az ernyőn, amelyet egy vastag sáv formájában észlelünk. Ha ezt a sávot lupéval, vagy leolvasó mikroszkóppal nézzük, ill. lencsével ernyőre képezzük, feltárul a finomszerkezete.
Megfigyelés: Hajszálvékony világos és sötét vonalak (erősítési és sötét kioltási helyek) követik egymást.
Magyarázat: Annak feltétele, hogy az ernyő tetszőleges P pontjában erősítés legyen az S1, S2C és ROP háromszögek közelítő hasonlóságát felhasználva határozható meg. (2.1.2. ábra)
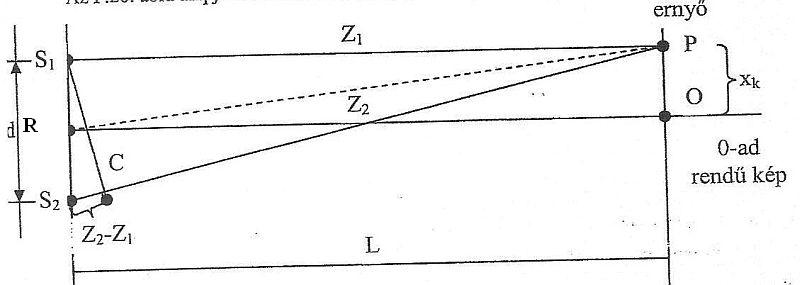
2.1.2. ábra (Forrás: Hadházy T., Nyilas I., Varga K.: Fizikai laboratóriumi gyakorlatok III., Bessenyei György Könyvkiadó, Nyíregyháza,2005, 43 old.)
Ezt felírva xk = kλL/d adódik. Két tetszőleges szomszédos világos vagy sötét csík távolsága pedig x = λL/d. Ezen összefüggés felhasználásával L és d ismeretében a kísérletben alkalmazott monokromatikus fény hullámhossza (λ) meghatározható. A fény koherenciahosszát úgy kapjuk meg, hogy a még megkülönböztethető kontrasztosságú erősítési helyek számát megszorozzuk a hullámhosszal. A kontrasztosság, azaz az erősítési és kioltási helyek megkülönböztethetősége, ugyanis a találkozó hullámok fázisviszonyától függ. Ha már nem azonos a találkozó hullámok fázisa, de még nem is ellentétes, azaz a koherenciahossz vége felé közeledünk, akkor a kontrasztosság csökken.
Feladat:
Figyelje meg rögzített L és d esetén az erősítési helyek távolságának hullámhosszfüggését! Az interferenciaképek megtekintéséhez kattintson ide!
Határozza meg a vörös fény koherencia hosszát, ha λ=639 nm!
A fényinterferencia az oka azoknak a tarka színjelenségeknek, amelyek természetes, vagy mesterséges fénynél észlelhetők igen vékony, (a megvilágító fény hullámhosszúságának nagyságrendjébe eső) rétegeken, mint pl. szappan hártyákon, vízen szétterülő olajrétegen stb. Ha a jelenség párhuzamos vékony lemezen jön létre, akkor az un. egyenlő beesés, ha ék alakú lemezen alakul ki, akkor az un. egyenlő vastagság görbéit látjuk. Az interferenciára képes (koherens) fénynyalábokat ezekben az esetekben intenzitás (amplitúdó) osztással állítjuk elő, s a jelenséget reflektált és áteső fényben egyaránt szemléltetjük.
Kísérlet : Egy planparalel üveglap és a ráhelyezett nagy görbületű síkdomború lencse közé bezárt levegőrétegen hozunk létre interferenciát. (Newton-készülék). Az eszközt optikai padra helyezve nagy fényerejű, leblendézett fényforrással világítjuk meg mintegy 10-15 cm távolságból és az áteső fényben keletkezett képet lencsével képezzük le a mintegy 1 m-re lévő ernyőre. A visszavert fényben kialakuló interferenciaképet úgy állítjuk elő, hogy a Newton készüléket kb. 30o-al elforgatjuk, és a keletkezett képet gyűjtőlencsével ernyőre képezzük.
Megfigyelés: Mind áteső, mind reflektált fényben, monokromatikus fényt alkalmazva, koncentrikus, a középponttól kifelé haladva sűrűsödő körsereget kapunk, melyben az erősítési helyeket világos, a kioltásokat sötét körök (Newton-gyűrűk) jelzik. Ha a kísérletet fehér fényű fényforrást használva végezzük el, akkor a gyűrűk színesek, egy-egy gyűrűn belül mindig a rövidebb hullámhosszúságú gyűrű sugara a kisebb. Megfigyelhető, hogy az áteső, ill. a reflektált fényben keletkezett kép éppen egymásnak fénytani reciproka. Míg áteső fényben a kép közepe világos, addig reflektált fényben sötét, s ahol áteső fényben erősítés tapasztalható, ott visszavert fényben kioltás látható.
Magyarázat: Az azonos d rétegvastagságnál kialakult erősítési helyeket összekötő görbe (egyenlő vastagság görbéje) kifogástalanul megmunkált lencse-lemez felület esetén szabályos kör. Az interferencia a lencse-lemez közé bezárt levegőréteg első és hátsó felületén történő visszaverődés eredményeként jön létre (reflektált fényben). Igazolható, hogy pl. monokromatikus, reflektált fényben az egyes erősítési helyek sugarai az r12: r22: r32 = 1 : 3 : 5:...szabályszerűséget követik. A jelenség a leképező fény hullámhosszának mérésére is felhasználható, a lencse R görbületi sugarának és a k-adik világos gyűrű sugarának ismeretében az rk2= (2k+1)Rλ/2 összefüggés segítségével, ahol k=0, 1, 2, ...
Feladat:
1. Állapítsa meg, hogy a 2.1.3. ábrán látható Newton-gyűrűs felvételek monokromatikus vagy fehér fényben készültek-e?
Válassza ki melyik felvétel készült áteső, melyik visszavert fényben.

2.1.3. ábra
2. A 2.1.4. ábrán egy szappanhártya-minimálfelület látható.
a.) Összetett vagy egyszínű fénnyel történt a megvilágítás?
b.) Az egyenlő beesés vagy az egyenlő vastagság görbéi láthatók?

2.1.4. ábra (Forrás: Kodansha's Programme for O.H.P. Physics, 1972)
3. Méréssel igazolja, hogy a 2.1.5. ábrán az egymást követő erősítési helyek sugarai követik a fenti szabályszerűséget.

2.1.5. ábra (Forrás: Kodansha's Programme for O.H.P. Physics, 1972)
Ha egy hullámtérbe olyan akadályokat, nyílásokat helyezünk, amelyek mérete nagyságrendileg összemérhető a hullámhosszal, akkor az ezek alkotta árnyéktérben is tapasztalunk hullámjelenséget. Ezt a hullámok elhajlása (diffrakció) okozza, és az elhajló hullámok interferenciájával magyarázható.
Kísérlet : A kísérleti elrendezés fényforrásaként az R1 rés szerepel, melyet fehér (összetett) vagy monokromatikus fénnyel világíthatunk meg. Az R1-ről kiinduló fényhullámok hullámterébe helyezzük az R2 nagyon keskeny, az R1-el párhuzamos rést, amelyen a fényelhajlás bekövetkezik. A jelenséget ernyőn, áteső illetve reflektált fényben egyaránt szemlélhetjük (Fresnel-féle diffrakció).
Megfigyelés: Fehér fényű fényforrás esetén a középső réskép fehér, jobbra és balra csökkenő intenzitású, ismétlődő színes csíkok láthatóak úgy, hogy egy színes sávon belül mindig a rövidebb hullámhosszúságú összetevő helyezkedik el a 0-ad rendű résképhez közelebb. Ha a kísérletet monokromatikus fényt alkalmazva végezzük el, a réskép két oldalán (0-ad rendű réskép) jobbra és balra erősítési és kioltási helyek sorozata látható (2.1.6. ábra).
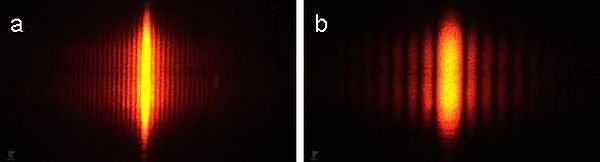
2.1.6. ábra
Észrevehetjük, hogy az erősítési helyek intenzitása (1., 2., 3., ... stb. rendű résképek) a 0-ad rendű résképtől távolodva rohamosan csökken, ellentétben az interferenciaképpel. Az R2 rés méretének változtatásával az elhajlási kép befolyásolható: ha a rést szűkítjük, az árnyéktérbe történő behajlás erőteljesebb, az 1., 2., 3-adrendű résképek távolodnak a 0-rendű résképtől, míg a rést nyitva ezek közelednek. Az alkalmazott fény hullámhosszát nagyságrendileg meghaladó R2 résméret esetén a jelenség csupán a réspofákon, mint nagyméretű tárgyak szélein, bekövetkező hullámelhajlásra korlátozódik.
Magyarázat: A jelenség elemi módon a Huygens-Fresnel elv, ill. a Fresnel-féle zónaelmélettel magyarázható. Az elmélet alapgondolata egy konstrukció. Ennek során az αk szög alatt elhajló fénynyalábot zónákra bontjuk úgy, hogy a szomszédos zónák fénysugarai rendre megfeleltetve egymásnak, egymáshoz képest λ/2 útkülönbségűek. Ekkor, pl. 5 db zóna esetén az első és a második, valamint a harmadik és negyedik zóna kioltja egymást, míg az ötödik zónából származó fény megvilágítást ad az ernyőn. 4 db zóna esetén azonban kioltást kapunk. A vázolt megfontolásokat folytatva azt kapjuk eredményként, hogy az ernyő azon helyein látunk erősítést, melyekre teljesül, hogy az intenzitásmaximumokhoz tartozó αk elhajlási szögekre a dsinαk= (2k+1)λ/2, míg az intenzitásminimumokhoz tartozókra α'k a dsinαk'= 2kλ/2 feltétel teljesül. Itt d a rés szélessége, k = ±1, ±2, ... A középső, 0-ad rendű maximumra a k=0 és α=0 igaz. Kimutatható továbbá, hogy a résen elhajló fény intenzitása az α elhajlási szögnek a függvénye.
Feladat:
A résméret (0,1 mm), a rés és ernyő távolság (55 cm) ismeretében határozza meg a vörös színű fény hullámhosszát, lemérve az első rendű erősítési helynek a 0-ad rendű erősítéstől való távolságát.
Az elhajlásjelenségek másik nagy csoportját az akadályokon bekövetkező elhajlások alkotják. Természetesen ezeknél is követelmény, hogy a hullámtérbe helyezett akadályok mérete nagyságrendileg a hullámhosszal összemérhető legyen. Fényhullámok esetén ez, pl. vékony drótszálak, vagy hajszál fény útjába történő helyezésével teljesül. Az akadályok szélein leszakadó hullámok csökkenő intenzitás-eloszlásának megfigyelésén túl érdekesebb az akadály mögötti árnyéktérbe behajló hullámok interferenciájának jelensége.
Kísérlet: Kísérleti összeállításunkban egy monokromatikus, vagy fehér (összetett) fénnyel megvilágított R rés szerepel fényforrásként. Ennek hullámterébe helyezzük a különböző méretű akadályokat (át nem látszó tárgyak). Az ezek mögötti árnyéktérben, ill. az akadályok szélein kialakuló jelenségeket ernyőn áteső, ill. reflektált fényben szemlélhetjük.
Megfigyelés: Egy vékony, átlátszatlan akadály árnyéka kis intenzitású világos és sötét, csíkokból áll, amelyek az árnyéktérbe behajló hullámok interferenciájának eredményeként keletkeznek. Figyeljük meg, hogy ezek száma csökken az akadály méretének csökkentésével, végül mindössze egyetlen erősítési hely látható (2.1.7. ábra). Az átlátszatlan akadályok szélének árnyékán sincs éles határ, ehelyett csökkenő intenzitású csíkok észlelhetők.

2.1.7. ábra
Magyarázat: A jelenségek elemi módon a Huygens-Fresnel elv, ill. a Fresnel-féle zónaelmélettel magyarázhatóak, matematikai leírásuk a Fraunhofer-féle elhajlás értelmezésével adható meg.
A transzmissziós (áteső fényben működő) rácsnak nevezzük a nagyszámú, egymástól egyenlő távolságban párhuzamosan elhelyezkedő rések összességét. Ha egy ilyen résrendszert hullámtérbe helyezünk, akkor a rácson átengedett fénynyalábok interferenciáját vizsgálhatjuk. Ez az interferenciakép az egyes elemi réseken elhajló hullámok találkozásával keletkezik. A transzmissziós optikai síkrács egy csiszolt üvegfelület, melyre egy speciális osztógéppel egyenlő közönként párhuzamos karcolatokat ejtenek. A fény a megkarcolt helyeken nem, míg a sértetlen felületeken áthalad. Az üvegfelület egy milliméteres intervallumára több száz, néha több ezer karcolat is jut. Egy sértetlen és egy megkarcolt felületrész együttes szélessége a rácsállandó (d).
Kísérlet : Üvegrácsot helyezünk az R rés elé úgy, hogy a rés és a rácson lévő karcolatok (elemi rések) párhuzamosak legyenek. A Franhofer-féle elrendezést alkalmazzuk, az elhajlási interferenciaképet gyűjtőlencsével képezzük le az ernyőre. Fényforrásként összetett fényű fényforrást, egy Hg-gőz lámpát alkalmazunk.
Megfigyelés: Az ernyő R réssel szemközti részén a résképet látjuk a megvilágító fény színében (0-ad rendű), ettől jobbra és balra a fényforrás színképét (első rendű színkép), amelyben a rövidebb hullámhosszúságú összetevő van közelebb az ernyő közepéhez (2.1.8. ábra). Kísérletünkben az ibolyaszín. Ezt követi mindkét oldalon a másod-, a harmad- stb. rendű színkép, melyek egyre nagyobb ernyőtartományokat fednek le, és a magasabb rendekben egymásra is eshetnek.

2.1.8. ábra
Kísérlet : Az előbb kísérleti elrendezésben a fényforrást kicseréljük egy monokromatikus fényforrásra, egy folytonos üzemű lézerre.
Megfigyelés: Ha fényforrásként monokromatikus sugárzót (pl. lézer, színszűrővel szűrőzött izzólámpa) használunk, akkor a résen való elhajláshoz hasonló képet kapunk, de most a világos helyek sokkal keskenyebbek, mint a sötét kioltási helyek. Az erősítési helyek intenzitáselosztása annál egyenletesebb, minél több elemi rés esik az optikai rács 1 mm-ére, azaz minél kisebb a rácsállandó.

2.1.9. ábra
Magyarázat: A sokréses rács által előállított elhajlási interferenciakép keletkezése elemi úton a Huygens-Fresnel elv segítségével magyarázható. Az R rés hullámterébe helyezet diffrakciós rács minden egyes rése elemi hullámcentrumnak tekinthető, amelyekből kiinduló hullámok találkozván bizonyos irányokban erősítést, míg más irányokban kioltást eredményeznek. A maximális erősítések αk irányait a dsinαk= kλ, ahol k = 0, ±1, ±2, ±3, ... feltétel szabja meg. Az el nem térített, αo=0 irányú sugarak a 0-ad rendű résképet adják, ettől jobbra és balra rendre az un. első-, másod-, ... rendű elhajlási vonalak láthatók (2.1.10. ábra).
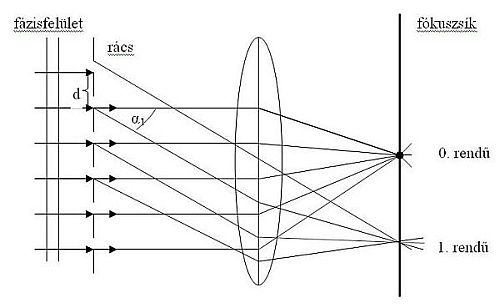
2.1.10. ábra (Forrás:Hadházy Tibor (szerkesztő), Nyilas István, Varga Klára: Fizikai laboratóriumi gyakorlatok III. főiskolai jegyzet, Bessenyei Könyvkiadó, Nyíregyháza, 2005. 47. oldal F.21. ábra)
Feladat:
Rendezze a rácsállandó csökkenése szerinti sorrendbe a monokromatikus fényben készült elhajlási képeket.
Magyarázza meg az összetett fényű fényforrással készített ernyőkép (2.1.8. ábra segítségével az elsőrendű rácsképen látható színek sorrendjét.
Kísérlet : Síkbeli keresztrácsot legegyszerűbben úgy kaphatunk, ha két vonalas rácsot, lehetőleg azonos rácsállandóval rendelkezőt, karcolataikkal merőlegesen egymásra helyezünk. Az így kapott rácsrendszert, ami a hétköznapi értelemben vett rács megfelelője, monokromatikus fényt sugárzó fényforrással (He-Ne gázlézer) világítjuk meg, s a keletkezett elhajlási interferenciaképet gyűjtőlencsével ernyőre képezzük (Fraunhofer-féle elrendezés).
Megfigyelés: Az ernyőn a 2.1.11. ábrán látható szabályos, síkbeli elhajlásjelenséget látunk.

2.1.11. ábra
Kísérlet : A keresztrácsot megvilágító fényforrást kicseréljük egy összetett fényű fényforrásra, egy Hg-gőz lámpára, és a keresztrács elé kb. 20 cm távolságra szűk kördiafragmát teszünk.
Megfigyelés: Színpompás jelenségben gyönyörködhetünk, az ernyőn a 2.1.12. ábrán látható szabályos, síkbeli elhajlásjelenséget látunk.

2.1.12. ábra (Forrás: Kodansha's Programme for O.H.P. Physics, 1972)
Magyarázat: Az ernyő közepén a körblende nulladrendű képét láthatjuk a megvilágító fényforrásnak megfelelő színben. Vízszintes és függőleges irányban a két vonalrács első-, másod-, harmad- ... stb. rendű elhajlási képei (spektrumai) láthatók a már megismert színsorrendet követve. E két irány között azonban további elhajlási képek helyezkednek el, melyek között az eligazodást sor- és oszlopindexek hozzárendelésével könnyíthetjük meg.
A síkbeli keresztrács elhajlási képén a függőleges és vízszintes vonalrács-képeken túli elhajlásjelenség a vonalrácsok metszéspontjain, mint elemi hullámcentrumokon bekövetkező fényelhajlás következménye. Mivel a 0o és 90o közötti irányokban a rácsállandó is változik, így ezekben az első-, másod-, ... stb. rendű elhajlási képek (spektrumok) a kördiafragma 0-ad rendű képétől más-más távolságra helyezkednek el.
Ha a fényelhajlást okozó rácspontokat a síkból kilépve térben is felépítjük (térbeli rács), akkor a kristályszerkezet tanulmányozásához elengedhetetlen elhajlási-interferenciaképeket állíthatunk elő röntgen fényt alkalmazva sugárforrásként.
Feladat:
A síkbeli keresztrács elhajlási képén határozza meg a 0o 90o közötti irányokban keletkező elhajlási képekhez tartozó irányszögeket.
Kísérlet : Egy mészpát kristályt helyezünk egy szöveget tartalmazó papírlapra.
Megfigyelés: A mészpát kristályon keresztül nézve a szöveget, kettőt látunk belőle (2.1.13. ábra).

2.1.13. ábra
Magyarázat: A kettős törés egy olyan optikai jelenség, amelynek során a tárgyra (közegre) eső fénysugár az azokon való áthaladás során két részre bomlik. Ez a jelenség optikailag anizotrop (többé-kevésbé rendezett) közegekben lép fel. Ezekben a közegekben a fényhullámok fázissebessége különböző irányokban más és más. Ez a jelenség a szabályos rendszerben kristályosodók kivételével kisebb-nagyobb mértékben, valamennyi természetben található kristálynál mutatkozik. Különösen szépen tapasztalható, pl. a mészpát és a kvarc esetében.
A természetes kettős törés mellett a mesterséges anizotrópia okozta mesterséges kettős törés jelenségével is gyakorta találkozunk. Mesterséges kettős törés jelenségköréből a feszültségi kettős törést demonstráljuk. Ilyen kettős törést produkálnak a mechanikai deformációnak kitett anyagok, de okozhatja a hirtelen lehűtött műanyagban keletkezett belső feszültség is.
Kísérlet : Összetett fénnyel megvilágított keresztezett állású polarizációs szűrök közé helyezünk műanyag vonalzót, s a keletkezett képet ernyőre képezzük le.
Megfigyelés: A vonalzó képén színes, szabálytalan alakú, színes interferenciamintázatot látunk (2.1.14. ábra).

2.1.14. ábra
Magyarázat: A kettős törés során a beeső fény intenzitása a közegben megfeleződik a rendes (ordinárius, minden irányban azonos sebességgel terjedő) és az extraordinárius (rendellenes, terjedési sebessége irányfüggő) sugár között. Mindkét sugár lineárisan polarizált, de egymásra merőleges síkban. Mivel a két sugár fázissebessége különböző, a kettősen törő közegből kilépve útkülönbséggel rendelkeznek, amely a közeg vastagságának megfelelő megválasztásával λ/4, λ/2, stb. lehet. Így elviekben ezek a sugarak interferencia-képesek. Interferenciajelenséget közöttük mégsem tapasztalunk csak akkor, ha a kilépő fényt polárszűrőn vezetjük át. Az Aragó-elv szerint ugyanis csak a párhuzamos polarizációsíkú fénysugarak interferencia képesek. (Két, egymásra merőleges síkban poláros fényhullám találkozásakor ugyanis az eredő intenzitás kifejezésében a cosα-val arányos interferenciás tag zérus, így a két hullám sem erősíteni, sem kioltani nem képes egymást.)
Az ernyőn látott kép fehér fényű fényforrást alkalmazva úgy keletkezik, hogy minden (elegendően, de nem túlságosan nagy) d vastagság és így minden fázis, ill. útkülönbség jelen van a kettősen törő anyagot elhagyó fényben, amelyet polárszűrön vezetünk át. (ld. Aragó-elv) A polárszűrők párhuzamostól eltérő állásaiban egyes színek interferenciásan kiszűrődnek a fehérből, a maradék színek miatt a látómező színes. Ha a d kicsi, a látómező csak szürke. Nagy d esetén a fehérből az adott λ spektrálszín kioltás miatt hiányzik, s az ernyőn ennek komplementer színe látszik. A színjelenség változik a második polárszűrő áteresztési síkjának változtatásával, de mechanikai deformáció hatására is.
Ez utóbbit hivatott szemléltetni a zselatinkockával végzett kísérlet.
Kísérlet : Összetett fénnyel megvilágított keresztezett állású polarizációs szűrök közé helyezünk egy zselatinkockát, s a keletkezett képet ernyőre képezzük le.
Megfigyelés: A zselatin kocka képén színes, szabálytalan alakú interferenciacsíkokat látunk, melyek attól függően változnak, hogy milyen irányból és mennyire erősen nyomjuk a kockát.
A bemutatott jelenség gyakorlati hasznosításaként különböző szerkezetek (szerkezeti elemek) üveg és plexi modelljein fellépő kettős törés vizsgálatából a szerkezetben fellépő feszültségekre lehet következtetni.
Magyarázat: Lásd az előbbi, vonalzóval végzett kísérletnél.
Kísérlet : Pollenszemcsékkel beszórt üveglapot lézer fénynyalábjának útjába helyezünk, s az elhajlított fényt lencse gyújtósíkjára képezzük le.
Megfigyelés: Az ernyőn koncentrikus, a középponttól távolodva csökkenő intenzitású világos elhajlási gyűrűk keletkeznek, amelyeket sötét koncentrikus körök választanak el (2.2.1. ábra).

2.2.1. ábra
Magyarázat: Egy felületen szabálytalanul elhelyezkedő, a fény hullámhosszával összemérhető méretű részecskéken szintén fényelhajlás következik be. Ebben az esetben az elhajlított fény intenzitása lényegesen nagyobb, mintha a jelenség egyetlen részecskén (szórócentrumon) következett volna be. Az ernyőn látható koncentrikus, a középponttól távolodva csökkenő intenzitású világos elhajlási gyűrűk és a közöttük lévő sötét koncentrikus körök sugara a megvilágító monokromatikus fényforrás hullámhosszától függ, vörös fényt sugárzó He-Ne lézer esetén nagyobb, mint a zöld fényt kibocsátó félvezető lézert alkalmazva.
A sok, rendezetlenül elhelyezkedő részecskén bekövetkező fényelhajlás is a fény hullámtermészetének bizonyítéka. Hasonló jelenség a párás időben a Hold körül kialakuló un. holdudvar, vagy a ködös időben az utcai lámpák körül keletkező fényudvar is.
A fénynyaláb útjába helyezett test, főleg, ha fekete színű, felmelegszik. A napfény melegét testünkkel is érzékelhetjük. Sok más példa is bizonyítja, hogy a fényben energia áramlik. Az energiaáramlás irányát a fénysugarak iránya adja meg. Megjegyzendő, hogy a fényforrások általában a látható fény mellett a spektrum más tartományaiban is, a hőmérsékleti sugárzók főként az infravörösben sugároznak, így a teljes sugárzási energiának csak egy része a szűkebb értelemben vett fényenergia.
Kísérlet : Egy fényelemet elektromosan összekötünk egy villanymotorral, majd lámpával megvilágítjuk a fényelemet.
Megfigyelés: A fényelemet megvilágítva, a villanymotor tengelyére erősített propeller el kezdett forogni.
Magyarázat: Mindkét esetben a fényforrásból kiinduló, energiával rendelkező fotonok a fényelemben belső fényelektromos hatás során fotoelektronokat váltanak ki. A fényelem, mint feszültségforrás fotoáramot indít a zárt áramkörében, s a kis elektromotor forgásba jön.
A fényben tehát energia áramlik, amely azzal a közeggel, amelyen áthalad, kölcsönhatásba lép. Ez a kölcsönhatás sokféle lehet (pl. erősen elnyelő fekete részecskéken elhajlik, a közegtől eltérő törésmutatójú, gyengén elnyelő részecskéken szóródik stb.).
Kísérlet : Kísérleti összeállításunkkal e kölcsönhatás egyik fajtáját, az un. inkoherens szóródást demonstráljuk. Vezessük át izzólámpa párhuzamossá tett fénynyalábját egy küvettán, amelybe eosin vizes oldatát töltöttük, majd helyezzünk a nyaláb útjába különböző színű színszűrőket.
Megfigyelés: A küvettán áthaladó fény kölcsönhatásba lép az oldat részecskéivel, másodlagos fényforrássá téve azokat. Figyeljük meg, hogy amíg vörös, sárga, vagy zöld színű színszűrőt használva, az áthaladó és az ernyőn foltot hagyó fénynyaláb színe megegyezik a színszűrőével, addig kék színű szűrőt alkalmazva, az ernyőn levő fényfolt bíbor-vörös.
Magyarázat: A fény-anyag kölcsönhatásnak ez a fajtája az inkoherens szóródás. A folyamat során a molekulák a beeső fényből energiát vonhatnak el, megnövelve ezzel saját rezgési vagy forgási energiájukat. Így a szórt fényben kisebb energiájú (nagyobb hullámhosszúságú, pl. vörös) komponensek is megjelennek, amelyek a beeső fényben nem voltak jelen. Ezek a beeső kék színhez adódva eredményezik a tapasztalt bíbor-vörös színt ( 2.2.2. ábra).
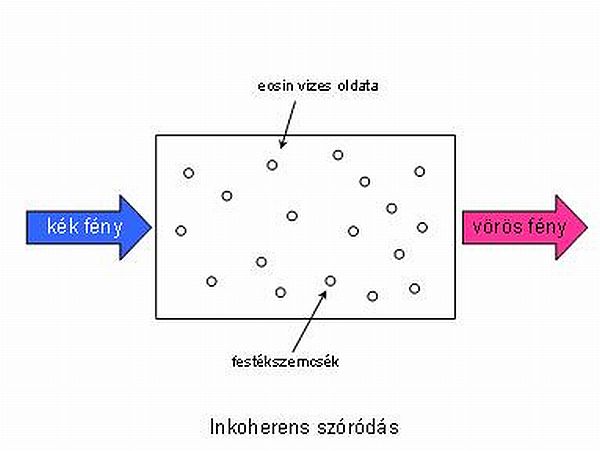
2.2.2. ábra
Feladat:
Indokolja meg, hogy az inkoherens szóródás összhangban van az energia-megmaradás általános elvével!
A diszperzió (színszóródás) is példa a fény és az anyag (közeg) kölcsönhatására. Oka, hogy anyagi közegekben a fény fázissebessége (és törésmutatója) függ a frekvenciától (hullámhossztól). Így ezekben az összetett (több hullámhosszúságú összetevőt is tartalmazó) fény alkotórészeire bomlik. A jelenséget, melyet Newton vizsgált elsőként, kísérletileg úgy észlelhetjük, ha keskeny fénynyaláb útjába üvegprizmát helyezünk.
Kísérlet : Izzólámpa fényével megvilágított rést képezünk le gyűjtőlencsével egy ernyőre, majd a lencse és az ernyő közzé helyezzük az üvegprizmát, ügyelve arra, hogy a prizma törőéle párhuzamos legyen a réssel. A keletkező kép javítható, ha a leképezést az ernyőre egy gyűjtőlencsével végezzük. A kísérlet második felében az ernyő helyére tesszük a kamerát.
Megfigyelés: A prizma fényútba helyezésével az ernyőn az eredetileg fehér réskép helyett színes sávok, un. spektrum (színkép) jelenik meg, melyen belül az eltérítés mértékének sorrendjében az alábbi főbb színeket lehet látni: vörös, narancs, sárga, zöld, kék, ibolya.
Magyarázat: Ez a jelenség a diszperzió (színszóródás), ami azt demonstrálja, hogy az anyag törésmutatója a fény színétől függ. Emiatt a prizmán áthaladó összetett fény az első és a hátsó oldalon is megtörik, majd a prizmából kilépve a hullámhosszától, színétől függően más-más irányban halad tovább (2.2.3. ábra).
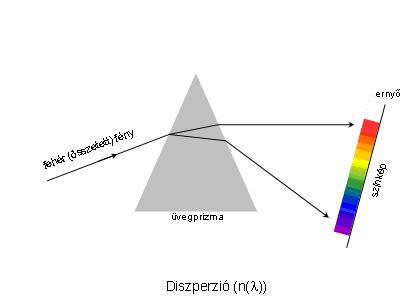
2.2.3. ábra
A spektrum nagyobb ernyőtartományra terjed ki, ha un. egyenes látású prizmát használunk.
A látható színkép hullámhossztartománya 380 nm (szélső ibolya) 760 nm-ig (szélső vörös) terjed. Ez a teljes elektromágneses színkép egy szűk, mindössze egy oktávnyi tartománya.
Kísérlet : Azt, hogy valóban a fehér fény felbontásáról van szó megmutathatjuk úgy, hogy a diszpergált fény útjába egy hengerlencsét helyezünk.
Megfigyelés: Ha nem takarunk ki a spektrumból egyetlen tartományt sem, akkor az ernyőn fehér színű réskép jelenik meg, tehát a spektrumszínek ismét fehér fénnyé egyesíthetők. Ha a spektrum egy tartományát kitakarva végezzük el a kísérletet, akkor a maradék összetevők keverékének színében látjuk a résképet. Ebben az esetben a vörös komponenst kitakarjuk, így a réskép kékeszöld színű lesz.
Kísérlet : A kísérleti elrendezésünkben kicseréljük a folytonos színképpel rendelkező izzólámpát Hg-gőz lámpára, melynek vonalas színképe van, azaz a színképe diszkrét vonalakból áll. A vonalak közül egyet kiválasztva vezessük át prizmán.
Megfigyelés: A Hg-gőz lámpa kiválasztott vonala a prizmán való áthaladás után nem bomlott további alkotóelemekre.
Magyarázat: A Hg-gőz lámpa vonalai egyszínű vonalak, azaz egy jól meghatározott hullámhossz tartozik hozzájuk. Ezért nem bonthatók tovább (2.2.4. ábra). Az ilyen fényt monokromatikus (egyszínű vagy homogén) fénynek nevezzük.
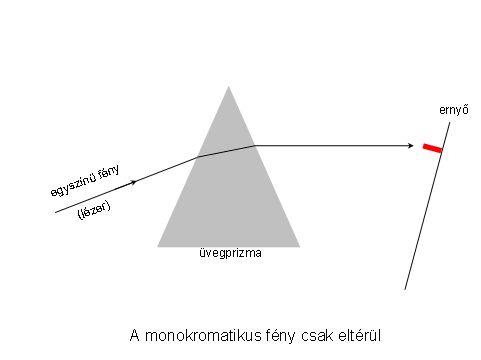
2.2.4. ábra
Kísérlet : A szigorú értelemben vett monokromatikusságot jól közelíti a lézerek fénye. Ejtsünk lézerfényt üvegprizmára, és egy ernyőn nézzük a színképet.
Megfigyelés: A lézerfénynek a prizmán való áthaladása során a fény minőségében változást nem tapasztalunk.
Fényszórás (fényszóródás) jelensége következik be akkor, ha egy közegben attól eltérő törésmutatójú, gyengén elnyelő részecskékre fény esik, s ezek a beeső fény hatására késleltetés nélkül másodlagos fényforrásokká válnak, melyek a beeső fény irányától eltérő irányokban is sugároznak. A jelenséget első ízben gőzködökön való fényáthaladás során Tyndall észlelte.
Kísérlet : Egy üvegkád vizén vezetünk át fehér fényt, majd a kádba a vízétől eltérő törésmutatójú szórócentrumokat juttatunk alkoholban oldott gyanta becsepegtetésével. Közben figyelemmel kísérhetjük a szórócentrumokkal teli kádban a fényviszonyokat, s a kádon átjutó fény színét.
Megfigyelés: Látható, hogy a szórócentrumok számának növelésével egyre narancssárgább, majd vöröses a kádon átjutó fény. Ugyanakkor képzeletben függőlegesen megfelezve a kádat, a fényforráshoz közeli rész kékes-fehér, míg a távolabbi sárga-narancssárga színű. A jelenség tehát függ a szórócentrumok számától. Ha a kádat 90o-al elfordítjuk, akkor a vöröses átjutó fény (ld. ernyőkép) sárgára, narancssárgára változik, jelezve, hogy most kevesebb szórócentrum került a beeső fény útjába. Ezzel a rétegvastagságtól való függést mutathatjuk ki.
Kísérlet : A szórócentrumokkal teli kádat három különböző színű fénynyalábbal világítjuk meg.
Megfigyelés: A vörös színű fény jut a legmesszebbre, míg a kék színű nyaláb teszi meg a legkisebb távolságot.
Magyarázat: A legegyszerűbb esetben a beeső fény hatására másodlagos fényforrássá úgy alakulnak a szórócentrumok (részecskékben, ill. molekulákban), hogy azokban, mint polarizálható töltésrendszerekben kényszerrezgések keletkeznek. Ennek következtében a szórócentrum a beesővel azonos frekvenciájú elektromágneses hullámot, fényt bocsát ki. A szóródott fény tehát csak a megvilágító fény hullámhosszait tartalmazza. A beeső fény hullámhosszánál jóval kisebb méretű részecskéken szóródott fény fázisa a gerjesztőjéhez képest állandó, ezért a szóródott fény a gerjesztővel interferenciaképes, koherens. Ez a koherens fényszóródás. A 2.2.5. ábrána szórt fény intenzitásának hullámhossztól való függését láthatjuk.
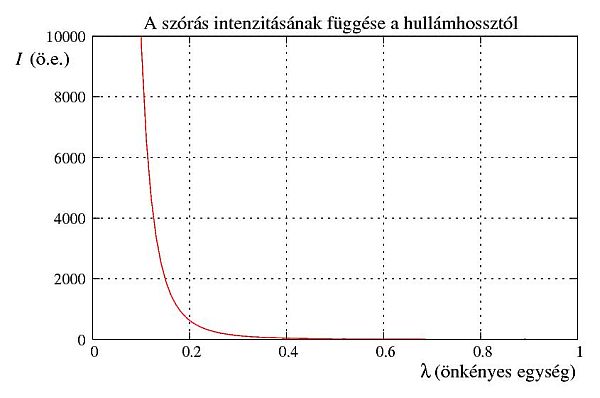
2.2.5. ábra
A szórt fény intenzitása tehát a hullámhossz negyedik hatványával fordítottan (míg a frekvencia negyedik hatványával egyenesen) arányos. A beérkező fehér (összetett) fényből először a rövidebb hullámhosszú komponensek (ibolya, kék) szóródnak ki, ezért kékeszöld színű a szórócentrumokkal teli kád fényforráshoz közeli fele. Ezek a színek, majd a zöld is, hiányoznak a továbbhaladó fényből, így a kádból kilépve az narancssárga, vörös (2.2.6. ábra).
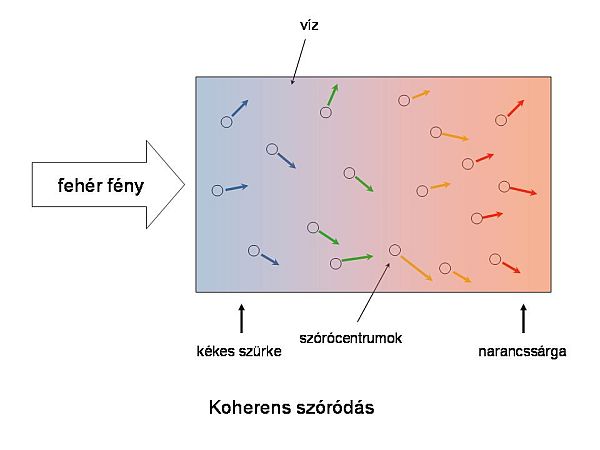
2.2.6. ábra
A fényszóródás jelensége a tapasztalatok szerint függ a szórócentrumok hullámhosszhoz viszonyított méretétől:

Kísérlet : Vörös, zöld és kék fényt kibocsátó LED lámpák fényét vezetjük át szórócentrumokat tartalmazó üvegkád vizén.
Megfigyelés: A vörös színű fény szóródik a legkevésbé, míg a kék a legjobban.
Magyarázat: Ha a szórócentrumok mérete sokkal kisebb a megvilágító fény hullámhosszánál, akkor un. Rayleig-féle szórásról (szóródásról) beszélünk. A szóródott fény intenzitásának a gerjesztő fény irányától mért szögeloszlását ábrázolva látható, hogy a fény döntő része a beesés irányába, ill. azzal ellentétes irányba szóródik, s a jelenség erősen függ a hullámhossztól (2.2.7. ábra).
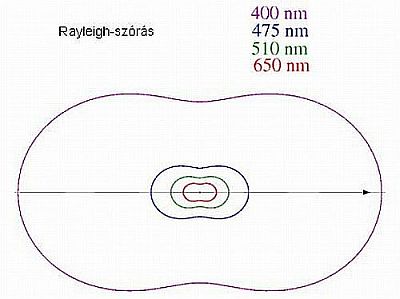
2.2.7. ábra
Legjobban az ibolya, majd a kék szín szóródik, legkevésbé pedig a vörös.
Fényszóródási jelenségek a környezetünkben
Ha a szórócentrumok gázmolekulák (pl. a földi légkört alkotó H, O2, N), akkor Tyndall-jelenségről beszélünk. Ez a magyarázata az ég kék színének. Döntő mértékben ugyanis a földi légkörbe érkező napsugarak rövidebb hullámhosszúságú komponensei (ibolya, kék) szóródnak. Mivel pedig a légkört alkotó gázoknak az ultraibolya ill. ibolya tartományban nagy az elnyelőképessége, az égboltot kék színűnek látjuk, mégpedig a Naptól minél távolabbi irányba nézünk, annál kékebbnek. A Holdon az égbolt a szórócentrumok hiányában fekete (2.2.8. ábra).

2.2.8. ábra (Forrás: http://www.nasaimages.org/)
A lemenő, ill. felkelő Nap színe azért narancsvörös, vörös, mert a delelési pozícióhoz képest sokkal nagyobb levegőréteg-vastagságot befutó napfényből útközben a kék, a zöld, s nagyrészt a sárga összetevő már kiszóródott (2.2.9. ábra). Jobb láthatósága miatt ezért célszerű a tiltó fényt vagy a megkülönböztető jelzést pirosnak választani.

2.2.9. ábra (Forrás: 3. kép http://hu.wikipedia.org/wiki/F%C3%A1jl:Glarus_Kloentalersee.jpg)
Amennyiben a szórócentrumok mérete a gerjesztő fény hullámhosszával összemérhető (óriásmolekulák, kolloidrészek, pára) megmarad a szóródott fény intenzitásának hullámhossztól való függése hasonlóan a Rayleigh-szóráshoz, de megváltozik annak intenzitás eloszlása. Ez az un. Mie-féle szórás, melynél a szórt fény zöme a beeső fény irányába szóródik (2.2.10. ábra).
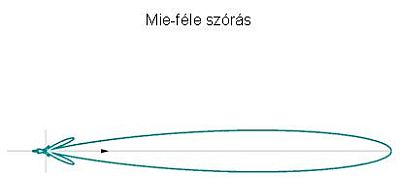
2.2.10. ábra
A füst, köd, felhő vízcseppje, hókristály stb. esetében, azaz amikor a szórócentrum lényegesen nagyobb a beeső fény hullámhosszánál, a hullámhosszfüggés lényegében eltűnik. Az ezeken szóródó fény színe a beesővel azonos. Ezért fehér vagy szürkés a vízcseppeket, jégkristályokat tartalmazó felhő, a köd, a sókristály stb.
Kísérlet : A szórócentrum méretváltozása okozta szóródási jelenségváltozás szemléltetéséhez két cigarettát gyújtunk meg. Az egyiket magára hagyva letesszük a hamutartó szélére, míg a másikba beleszívunk, és a kifújjuk a füstöt.
Megfigyelés: A magára hagyott cigaretta felszálló füstje kék színű, míg a kilélegzett (kifújt) füst fehéres-szürke.
Magyarázat: A hamuzó szélére tett cigaretta felszálló füstje azért kék, mert a papír, dohány felszálló kisméretű égéstermékei a hullámhosszal összemérhető méretűek, így rajtuk a szóródás hullámhosszfüggő. A belélegzett és kifújt dohányfüst fehéres-szürke színét az magyarázza, hogy tüdőnkben ezekre a kis égéstermékekre pára kondenzálódott, méretük megnövekedése miatt a szóródás hullámhosszfüggése eltűnt, rajtuk a fehér lámpafény, napfény szóródik.
Hasonló módon magyarázható a nagy magasságban közlekedő repülőgép kondenzcsíkjának keletkezése, amely a gép felszállásakor a tér túltelítetlenségének hiányában még nem látható ( 2.2.11. ábra) .

2.2.11. ábra
Bizonyos közegek a rajtuk áthaladó fényt (sugárzást) részben vagy teljes egészben elnyelik. Ez az abszorpció jelensége. Az abszorpció során a fény energiavesztesége az anyag belső energiájának növelésére, vagy másodlagos sugárzás keltésére fordítódik (lumineszcencia). Sokszor a közegben az abszorpció mellett fényszóródás is fellép. A két jelenséget együttesen extinkciónak mondjuk.
Kísérlet : A kísérleti elrendezésben leblendézett párhuzamos fehér fénynyalábot vezetünk át fényelnyelő közegeken, pl. káliumpermanganát, majd rézszulfát vizes oldatán. Az áthaladó fény intenzitását az általa keltett fotoáram erősségével jellemezhetjük.
Megfigyelés: A színes oldaton áthaladt fény intenzitáscsökkenése függ az oldat milyenségétől azaz hogy káliumpermanganát vagy részszulfát vizes oldatát helyezzük a fény útjába. Ugyanazon oldatból, ha a küvetta hosszabbik oldala mentén halad a fény, akkor nagyobb mértékben nyelődik el, mint amikor a küvetta rövidebb oldala mentén megy. Ha a fényforrásunk elé színszűrőket helyezünk, akkor azt tapasztaljuk, hogy az elnyelődés mértéke függ a küvettát megvilágító fény hullámhosszától is.
Magyarázat: A színes oldatok fényelnyelésének törvényszerűségét a Lambert-Beer törvény írja le, mely kifejezi, hogy az elnyelő közegekben a fényintenzitás exponenciálisan csökken, azaz I(x) = I0e- k (λ) x , ahol Io a küvettába lépő, I(x) az abban x távolság megtétele után mérhető fényintenzitás, k(λ) az extinkcióállandó, ami az anyagi minőségtől és a hullámhossztól függ. Ha a közegben a fény nem szóródik, akkor a k-t abszorpció állandónak nevezzük A közeg fényelnyelését jellemző abszorpciós együtthatót a hullámhossz függvényében ábrázolva az abszorpciós színképet kapjuk.
Fényelnyelődés jelensége a környezetünkben
Látható a 2.2.12. ábráról, hogy a víz alig nyel el a látható fény kék, kékeszöld tartományában, ugyanakkor erőteljesen elnyeli a vöröset. Ez magyarázza a nagy rétegű víz természetben tapasztalt színét.
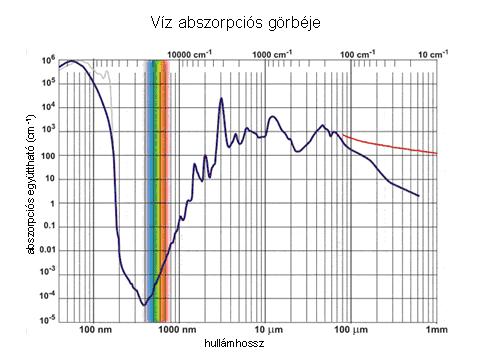
2.2.12. ábra (Forrás:http://en.wikipedia.org/wiki/File:Water_absorption_spectrum.png)
Kísérlet : Összeállításunkkal megvizsgálhatjuk a különböző színes oldatok, színes közegek abszorpciós színképet. Fényforrásként pontfényizzót használva, az áthaladó fényt prizmára ejtjük, majd gyűjtőlencsével ernyőre képezzük.
Megfigyelés: Mivel folytonos színképet adó izzólámpát használunk fényforrásként, az ernyőn látható kép az illető közegre jellemző abszorpciós spektrum. A hiányzó (sötét) tartományok az illető oldatra (színszűrőre) jellemző abszorpciós sávok. Az abszorpciós színkép jellemző az adott közeg anyagi minőségére. Oldatoknál az oldószer és az oldott anyag abszorpciós színképe együttesen jelenik meg. Ha az abszorpciós színképben szereplő színeket hengerlencsével összegyűjtjük, az oldat (színes közeg) színét kapjuk vissza, azt a keverékszínt, ami a prizmával való felbontás előtt az ernyőn megjelent.
A szín kifejezés a fizikában a fény bizonyos hullámhossz (frekvencia) -tartományba eső részének jellemzésére szolgál. Fiziológiai értelemben a szín a szemünkben kiváltott inger, illetve az ennek hatására keletkező érzet. Az emberi szem nagyon érzékeny színdetektor, sokezer színárnyalat megkülönböztetésére képes.

2.2.13. ábra
Környezetünk tarka színvilága (2.2.13. ábra) különböző fizikai jelenségek eredménye, ilyenek pl. a diszperzió, az abszorpció, a reemittálás (újra kibocsátás), interferencia stb. Keletkezésük magyarázata is különböző. A tárgyak, színek látványáért, jelentős részben, az anyagot alkotó atomok külső elektronjai a felelősek. Ezek ugyanis a beeső fény hatására kényszerrezgést végeznek, s mint elemi antennák, maguk is elektromágneses sugárzást bocsátanak ki ( 2.2.14. ábra).
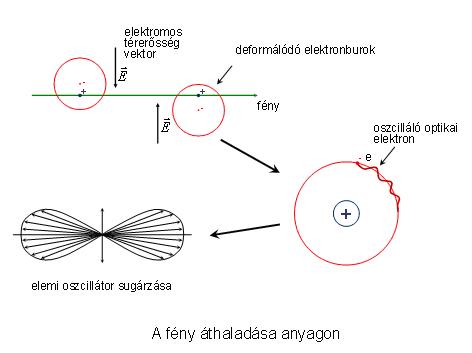
2.2.14. ábra
Az atomok szabályos, vagy közelítően szabályos elrendeződése esetén (szilárd anyagok, folyadékok) ezek összegződése adja a visszavert nyalábot, míg áteső fény esetében interferenciásan adódnak hozzá a beeső fényhez. A körülöttünk lévő legtöbb szín a preferált abszorpció eredménye. (virágok, madarak, festékek stb.) A festékmolekulák abszorpciója az egész látható színképet lefedi az anyag saját színének kivételével.
Kísérlet : Különböző színű (fehér, fekete, színes) kartonlapokat világítunk meg fehér fénnyel, majd fehér színű kartonlapra ejtjük a színszűrűvel megfestett fényt.
Megfigyelés és magyarázat: Ha minden látható frekvencián van abszorpció, a tárgyak feketék, ugyanakkor fehérek, ha a látható fény minden összetevőjét reflektálják. A színes papírlapok a fehér fényből a színüknek megfelelőt verik vissza, mert a fény belép a színes papírrostokba, amely elnyeli egy részét. Mire a visszavert fény a szemünkbe jut, egy szűk színtartományon kívül az összes többit gyengíti az abszorpció. A zöld színű papírból csak a zöld fény tud kiszabadulni, visszaverődni, a vörösből a vörös, stb. Ha nincs a beeső fényben olyan színtartomány, amelyet a tárgy visszaverni képes, akkor színe fekete.
Kísérlet : Hasonlóan, megvizsgálhatjuk színes üvegek (színszűrők) viselkedését is.
Megfigyelés: Látható, hogy pl. a vörös színű szűrő átengedi a vörös spektrumtartományt, az összes többit gyengíti, vagy elnyeli. A zöld éppen fordítva viselkedik (kiegészítő színek). A színszűrőn átjutó fényt hengerlencsével összegyűjtve a színszűrő színét kapjuk vissza.
Magyarázat: A színszűrő felületére érkező fény egyik része visszaverődik (reemittálódik), másik része abszorbeálódik a festékmolekulákban. Vörös színű színszűrő esetén ezért a visszavert fény vörös, az áteső fény (mivel a festékmolekulák a színkép részeinek kivonásával működnek, s így jelen esetben a zöldet nyelik el) szintén vörös. Amilyen színű fényt tehát a festett üveg visszaver, azt a tartományt át is ereszti.
Kísérlet : Fehér fényű fényforrással, majd nátriumlámpával (Na-D lámpa) világítunk meg különböző színű virágokat. (Fehér, sárga, piros)
Megfigyelés: A látvány nem azonos. Míg pl. a sárga színű virág színe mindkét fényforrás estében sárga, addig a piros színű virágokat szürkés-feketének (feketének) látjuk a nátriumlámpa fényében.
Magyarázat: A nátriumlámpa vonalas színképű fényforrás, színképe vöröset (leszámítva az elektródák izzása miatti gyenge hátteret) nem tartalmaz. A vörös színű virágok pedig a rájuk eső fényből ezt a tartományt tudnák visszaverni, mivel pedig ez esetünkben hiányzik, a színük szürkés-fekete.
Tartalom
Feladat: Mérje meg az étolaj sűrűségét! Függesszen fel egy hurkapálcát a közepénél (vízszintes helyzetben) egy fonálra! Mindkét oldalra függesszen fel nehezéket, úgy hogy ismét vízszintes legyen a pálca! Az egyik testet lógassa bele először vízbe, majd az étolajba, és mindkét esetben egyensúlyozza ki a pálcát a másik test elmozdításával. Mérje meg a szükséges adatokat vonalzóval, keresse meg a víz sűrűségét függvénytáblázatban, majd számítsa ki az étolaj sűrűségét!
A mérés elvégzése után válaszoljon a következő kérdésre: Függ-e a mérés pontossága a nehezék sűrűségétől és a nehezéket felfüggesztő fonal hosszától?
Eszközök: hurkapálca, cérna, vagy fonal, 2 db 10-es (vagy nagyobb) anyacsavar, nagyobb műanyag gyöngy, pohár, víz, étolaj, vonalzó
A mérés menete: A 3.1.1. ábra bal oldali részén látható módon a hurkapálcát függesszük fel egy vékony cérnára a középpontjában, majd mindkét végéhez közel egy-egy kb. 4cm hosszú cérnaszálra egy-egy azonos tömegű anyacsavart úgy, hogy vízszintes helyzetben, egyensúlyban legyen a hurkapálca. Mérjük meg az l1, l2 távolságokat. Ezután a 3.1.1. ábra középső része szerint az m1 tömeget vízzel töltött pohárba merítjük, és eltoljuk az m2-t az egyensúly létrejöttéig, és megmérjük az lvíz távolságot. Kivesszük a testet a vízből, szárazra töröljük, majd olajba merítjük, m2 eltolásával beállítjuk az új egyensúlyt, és megmérjük lolaj távolságot a 3.1.1. jobb oldali részlete szerint. Ezután egy üveggyöngyre kicseréljük az 1-es anyacsavart és megismételjük a mérést. Az egész mérést ismételje meg úgy is, hogy a cérnaszál 10 cm hosszú legyen.
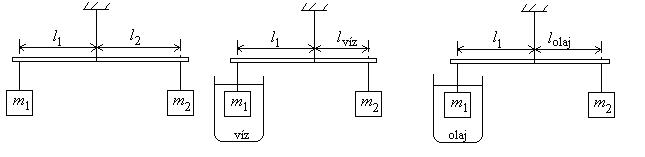
3.1.1. ábra
Feladat: Vizsgálja meg, hogyan függ kis szögkitérések esetén a fonálinga lengésideje a felfüggesztő fonál hosszától!
A mérés elvégzése után válaszoljon a következő kérdésekre:
a.) Miért nevezhetik a 99,4 cm hosszúságú fonálingát másodpercingának?
b.) Hogyan lehetne fonálinga segítségével meghatározni a szabadesés gyorsulását?
Eszközök: fonál (ne nyúljon meg!), a fonálra függeszthető kisméretű nehezék (anyacsavar), stopperóra (kihasználhatjuk egy mobiltelefon, vagy egy karóra stopperóra-funkcióját), mérőszalag, milliméter-papír.
A mérés menete: Függesszük fel az ingát úgy, hogy lengése ne ütközzön akadályba! Ügyelni kell a kis szögkitéréssel (<5?) történő lengés beállítására! Öt különböző hossznál mérjük meg a lengésidőt! Az időmérés pontosságát úgy fokozhatjuk, hogy 20 lengés együttes idejét olvassuk le a stopperről.
Kis szögkitérések esetén a fonálinga lengésidejét a következő összefüggés adja meg: T2=4π2l/g, ahol l az inga hossza, g a mérés helyén uralkodó gravitációs térerősség nagysága. A mérési sorozatnak igazolnia kellene, hogy az inga lengésideje egyenesen arányos hosszának négyzetgyökével. A probléma egyszerűen, linearizálással oldható meg. Ábrázoljuk a lengésidő négyzetét az inga hosszának függvényében. Pontos mérés esetén egyenest kapunk. Az egyenes meredekségéből számítsuk ki a g értékét!
Feladat: Határozzuk meg minél pontosabban egy gumiszál megnyúlás-erő grafikonját! Számítsuk ki a gumiszál átlagos rugalmassági (rugó-) állandóját! Írja le a kísérletnél használt eszközöket, a mérési eredményeket foglalja táblázatba, majd értelmezze a kapott eredményt!
Eszközök: kb. 50 cm hosszú kerékpár szelepgumi (lehet kalapgumi, modellező gumi), mérőszalag, vonalzó, súlyok (egyenlő tömegű nagyobb anyacsavarok, vagy 50 g-os súlyok 5-8 db), egy kis serpenyő, amibe a súlyok helyezhetők, pálca.
A mérés menete: A 3.3.1. ábrán látható módon a gumiszál végeire szorosan kötelet erősítünk, egyik végénél felfüggesztjük, másikra egy serpenyőt, vagy egy hurkot teszünk a súlyok elhelyezésének megkönnyítése miatt. A pálcát rögzítsük vízszintesen a serpenyő aljára! A gumiszál nyúlását a pálca elmozdulásából határozzuk meg, egy vonalzó segítségével. A mérést végezzük el legalább öt különböző terhelést alkalmazva, növekvő és csökkenő terhelés mellett is!
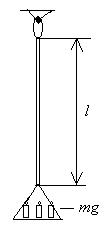
3.3.1. ábra
Feladat: Határozzuk meg egy kivehető polc anyaga és néhány sima oldallappal is rendelkező tárgy (könyv, vonalzó, ceruza, pénzérme, radír) közötti tapadási együttható értékét!
Eszközök: lejtő, melynek a magasságát tudjuk finoman változtatni (kb. 50 cm hosszú), vonalzó, tetszés szerinti tárgyak: könyv, vonalzó, ceruza, pénzérme, radír
A mérés menete: A lejtő felső végét lassan emeljük, amíg a lejtőn lévő test meg nem mozdul. Majd ebben a magasságban rögzítsük a lejtőt, és mérjük meg a magasságát! A magasság és a lejtő hosszának ismeretéből számítsuk ki a lejtő hajlásszögét!
A lejtőn lévő test egyensúlyban van mindaddig, amíg a tapadási erő el nem éri maximális értékét. Ha ezután is növeljük a lejtő hajlásszögét, akkor megcsúszik a test. Egyensúly esetén a testre ható erőket a 3.4.1. ábra mutatja. A tapadási erő maximumát, a megcsúszás pillanatában vizsgáljuk. A mérést végezzük el 5-10-szer mindegyik test esetén.
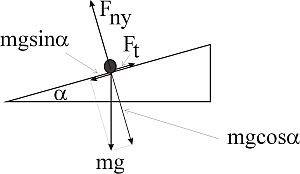
3.4.1. ábra
Feladat: Határozza meg a csapvíz felületi feszültségét egyetlen pipetta segítségével! Majd a felületi feszültség ismeretét felhasználva mérje meg a fólia vastagságát!
Felhasználható eszközök és anyagok: pipetta, Petri-csésze, 2 db 5x5 cm-es üveglap, alkoholos filc, műanyag fólia, olló, gumigyűrű, cérna, vonalzó, tolómérő
A mérés menete: A pipettából csepegtessen ki ismert térfogatú vizet, számolja a cseppek számát! Mérje meg tolómérővel a pipetta végének 2r átmérőjét! Ha nem rendelkezik tolómérővel, akkor tekerjen a pipetta végére ismert számú menetben cérnát. A felhasznált cérna hosszából határozza meg a pipetta végének külső kerületét. Ezen adatokból számítsa ki a felületi feszültség értékét! Ezzel az eljárással elég jó becslés nyerhető a felületi feszültségre. A cseppre a leszakadás pillanatában F ≈ α2rπ felfelé mutató erő is hat.
Alaposan tisztítsa meg az üveglapokat, és a két üveglap közötti távolságot változtassa! A két üveglap közé, a függőleges oldalaknál, mindkét oldalon a szürkével jelölt helyekre tegyen száraz 10 ill. 15 db egymásra helyezett befőző fóliából vágott vékony téglalap alakú csíkot, minkét oldalra azonos számút! Majd a két üveglapot szorítsa össze egy gumigyűrűvel! Az egyik üveglapra húzzon egy egyenes vonalat az alkoholos filccel (csak száraz üveglapon fog). A 3.5.1. ábra szerint mártsa bele a vízbe annyira, hogy a megrajzolt vonal a vízszinttel kerüljön azonos magasságba! Rajzolja meg a két üveglap közötti vízszintet is! Vegye ki az üveglapokat a vízből és mérje meg a két megrajzolt vonal távolságát! A víz felemelkedéséből becsülje meg a fólia vastagságát! Vegye figyelembe, hogy a két üveglap közötti folyadék felszínének alakja félhengerrel közelíthető, és nem félgömbbel, mint a kapillárisok esetében. A fóliák nagyon különböző vastagságúak. Lehet, hogy el kell térnie a megadott rétegszámtól. Könnyebb a mérés, ha kevesebb, de vastagabb műanyag fóliát használ! Mindig száraz fóliát használjon!
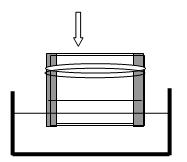
3.5.1. ábra
Feladat: Egy zenei CD-t rácsként használva, határozzuk meg egy lézeres mutatópálca fényének hullámhosszát!
Eszközök: CD-lemez, lézeres mutatópálca, állvány a befogásához (ruhacsipesz), hungarocell, vagy hullámkarton, papír, tű, szögmérő, vonalzó.
Munka közben vigyázzon a CD-lemez felületére, hogy az ne szennyeződjön el, és különösen a karcolódástól óvja!
Ha egy zenei CD-t, vagy számítógépes CD-adathordozót megvizsgálunk, akkor annak egyik oldalát ezüst, vagy zöldes színűnek látjuk. Nézzük egy távoli fényforrás képét a CD-n való visszaverődés után! A szivárvány színeit figyelhetjük meg. A CD-n az adatokat optikai elven olvassuk ki, melyek egy spirális mentén vannak elhelyezve. Ha ennek a spirálisnak egy kis részét nagy nagyítású mikroszkópon át megnézzük, akkor 1 mm-en 600 sávot találunk. A nagyon pontosan azonos távolságban elhelyezkedő sávok, a rájuk eső fényt az optikai rácshoz hasonlóan elhajlítják. (Egy-egy ilyen sáv mentén vannak, pl. a zenét leíró megfelelő jelsorozatok. Ez utóbbiak jelenlétét ebben a kísérletben nem figyeljük meg.) A sávok sorozata optikai (kör-)rácsként viselkedik. Egyszerűség kedvéért csak a merőlegesen ráeső fény elhajlását vizsgáljuk. A lemez belsejében levő reflexiós réteg miatt a megvilágítás irányában figyelhetünk meg nagyon keskeny nyalábokban, a merőlegesen beeső fényhez képest szimmetrikusan. Mérjük meg az erősítés irányaihoz tartozó szögeket! Jobbra és balra is két ilyen irány figyelhető meg!
A mérés menete: Helyezzük a papírt a hungarocell lapra, lehetőleg ennek magassága közel legyen a lemez vízszintes átmérőjének magasságához a 3.6.1. ábra bal oldali részlete szerint! Világítsuk meg a lézeres mutatópálcával a CD-lemez adathordozó részét merőlegesen (ruhacsipesszel rögzítheti a lézer kapcsológombját)! Addig kell mozgatnia a lézert (vagy a lemezt), amíg a lemezről az eltérítés nélkül visszaverődő fény visszajut a lézerbe! Az eredeti és az elhajlási irányokat a megvilágítás közben meg kell jelölni! Ezt úgy tehetjük, hogy egy hosszabb varrótűvel kilyukasztjuk a papírt a fénysugarak mentén néhány pontban (ezt megkönnyíti a papír alatt elhelyezett hungarocell, vagy karton). A kísérlet végén, kapcsoljuk ki a lézert, vegyük le a papírt. A papíron kössük össze a megfelelő pontokat vonalzóval, ehhez segítséget ad a 3.6.1. ábra jobb oldalán látható vázlat! Az azonos rendben visszavert sugarakhoz tartozó egyenesek szögét mérjük meg!
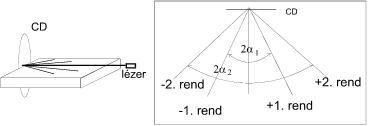
3.6.1. ábra
A mérés elméleti alapja:
Jelöljük d-vel a két szomszédos karcolat távolságát (rácsállandó), és vizsgáljuk meg, hogy mi a feltétele, hogy a szomszédos résekből kilépő fénysugarak erősítsék egymást:
Az elhajlított sugarak akkor erősítik egymást, ha a szomszédos résekből kiindulók is erősítik egymást: dsinαk = kλ, ahol k egész szám. Az összefüggésben szereplő mennyiségek jelentését leolvashatjuk a 3.6.2. ábráról.
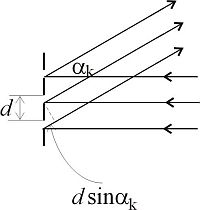
3.6.2. ábra
Ajánlott irodalom:
Erostyák J., Litz J. (szerk.): A fizika alapjai (Nemzeti Tankönyvkiadó, Budapest, 2003)
Budó Á.: Kísérleti fizika I. (Tankönyvkiadó, Budapest, 1981)
Budó Á., Mátrai T.: Kísérleti fizika III. (Tankönyvkiadó, Budapest 1977)
Bernolák K.: A fény (Műszaki Könyvkiadó, Budapest, 1981)
Weisskopf, V. F.: Válogatott tanulmányok (Gondolat, 1978)