Tartalom
- Előszó
- 1. A fény abszorpciója és emissziója
- 2. Az abszorpció és erősítés telítődése, vonalkiszélesedés
- 3. Rezonátorok mátrixoptikai leírása
- 4. Gauss nyalábok
- 5. Lézerek gerjesztése
- 6. Folytonos lézerműködés
- 7. Tranziens lézerműködés
- 8. Szilárdtestlézerek
- 9. Félvezető lézerek
- 10. Fényvezetőszál-lézerek
- 11. Festéklézerek
- 12. Gázlézerek
- 13. Szabadelektron lézer
- 14. Ultrarövid lézerimpulzusok torzulásai
- 15. Lézerimpulzusok diagnosztikája
A lézerek 1960-as felfedezése egy hosszú és bonyolult fejlődés eredménye, amely nem csak tisztán tudományos, hanem részben társadalmi feltételek meglétét is igényelte. Mint később látni fogjuk, fizikai szempontból a legalapvetőbb ismeretek, a kényszerített emisszió fogalma, a statisztikus fizika alapvető eredményei 1917 óta rendelkezésre álltak. Ebben az időszakban (a század elején) az atomfizika, a spektroszkópia, a magfizika és a kvantummechanika volt az érdeklődés homlokterében és produkálta az új és izgalmas eredményeket. Ahhoz, hogy egy anyagban optikai erősítést hozzunk létre az szükséges, hogy a hőmérsékleti egyensúlyban felvett eloszlásoktól jelentős mértékben eltérő helyzetet hozzunk létre, azaz populáció inverziót (amikor több részecske van gerjesztett állapotban mint alapállapotban). Ez a jelentős mértékben nem egyensúlyi helyzet nem valósítható meg egyszerű módszerekkel, történtek ugyan kísérletek a kényszerített emisszió megfigyelésére de eredmény nélkül. Az elektromos jelek erősítése elektroncsövekkel ezzel párhuzamosan a mérnöki tudomány részévé lett, a negatív és pozitív visszacsatolás tulajdonságai az oszcillátorok megvalósítása mind a szükséges előfeltételek közé tartozott. Sajnálatos lökést adott a fejlődésnek a második világháború többszörösen is. Egyfelől az emberiség történetében először nem csak katonák, fegyverek és gazdaságok harca folyt, hanem a tudomány és technika eredményeinek versenye is. Ennek az eredménye többek között a radar, az infravörös képerősítő éjjellátó készülék és nem utolsó sorban az atombomba. Mindezek a fejlesztések az idő rövidítésére a fizikusok, vegyészek és mérnökök szoros együttműködésére voltak alapozva, így a mérnöki gondolkodás behatolt a fizikába és kémiába. Másfelől a világháború befejeztével a rádiótechnika eredményei valamint részben feleslegessé vált eszközei nagy lökést adtak a rádióhullámú spektroszkópia fejlődéséhez. Ez a hullámhossz az, ahol viszonylag könnyen lehet erősítést és oszcillátort létrehozni (ez az információ már Einstein 1917-es publikációjában is benne volt). Így már érthető, hogy először a maser-t (Microwave Amplification by Stimulated Emission of Radiation rövidítésére alkotott betűszó) fedezték fel 1954-ben az ammónia 24 GHz-es átmenetén. A populáció inverzió létrehozása az ammónia két állapotának eltérő mágneses tulajdonságai alapján a molekulák szétválogatásával történt. Rövid idő múlva már szilárd (kristályos) anyagokban is tudtak maser-eket gerjeszteni. Jellemző az új eredmények gyors szaporodására és nagy számára, hogy 1960-ban Maiman dolgozatát a rubin optikai maser-ről nem fogadták el, mert a folyóirat szerkesztőbizottsága úgy döntött, hogy maser-re vonatkozó dolgozatot nem fogad el többé (6 évvel a felfedezése után!).
Az optikai tartományban működő oszcillátorokat a "Light Amplification by Stimulated Emission of Radiation" kifejezésből alkotott laser betűszóval nevezték el. A szó kiejtése alapján, a magyar nyelvben a lézer elnevezés is használatossá vált még a szaknyelvben is. A lézerek felfedezése után gyors és azóta is növekvő érdeklődés kísérte a lehetséges alkalmazásokat, mára csak a lézerek forgalma a világgazdaságban eléri a 10 milliárd dolláros szintet. Az alkalmazások igénye az optikai módszerek fejlődésének jelentős lökést adott, szerepe átértékelődött. Mára a lézerek az autógyártás nélkülözhetetlen technológiai elemévé (vágás, fúrás, hegesztés, edzés) váltak, a mikroelektronikai eszközök méreteinek csökkentését szolgáló verseny az éppen használt excimer lézer hullámhosszától függ. A fényvezető szálak jeltovábbítási alkalmazásai is a lézerek felfedezése után indultak robbanásszerű fejlődésnek, és váltak mára hétköznapi eszközökké a híradástechnikában és az informatikában. A szemészetben alkalmazott szaruhártya megmunkálással 12 dioptriás korrekcióra van lehetőség. Az optikai jelfeldolgozás olyan eszközei fejlődtek ki és váltak közönséges fogyasztási cikkekké mint a CD és DVD lejátszók, CCD kamerák, vagy a mikrobolométeres infravörös éjjellátó kamerák. Az itt felsorolt inkább csak jelzésértékű alkalmazások egy új komplex tudományos-ipari területet alkotnak melyet az elektronika mintájára fotonikának neveznek, mivel itt az elektronok helyett fotonok az erősítés a detektálás fő szereplői.
Ez az digitális tananyag a tudományegyetemek mester szakos hallgatói számára készült, az optika, atomfizika alapjainak ismeretét tételezi fel. Az egyes fejezetek bevezetése többnyire csak az algebra ismeretét kívánja meg, egyebekben a differenciál és integrálszámítás alapjainak ismeretét várjuk el. A tananyag a Fizikus MSc szakos hallgatók törzsmoduljának a részét képezi. Célja, hogy a lézerfizika tudományterület alapjaival megismertesse az Olvasót. Az 1-4 fejezetek bevezető jellegűek. Az 5-7 fejezetek általánosan foglalkoznak a lézerfizika alapjaival, míg a 8-13 fejezetek az egyes speciális lézertípusokat ismertetik. A 14. fejezet a lézerből kilépő fényimpulzusok tér- és időbeli tulajdonságainak a változásával foglalkozik, míg a 15. fejezet a rezonátorból kilépő fénynyaláb tulajdonságainak a mérését tárgyalja. Mivel fejezetek jelentős részben egymásra épülnek, ezért a tananyag lineáris, sorrenben történő feldolgozását javasoljuk.
A tananyag a TÁMOP-4.1.2.A/1-11/1 pályázat keretein belül készült.

Tartalom
A lézerek működésének fizikai alapjait a klasszikus fizika és a kvantummechanika egyaránt képes leírni. Itt most a megértés történelmi útján végigjárva egy szemléletes (eredetileg 1914-ben Einstein által publikált) gondolatmenettel mutatjuk be a legalapvetőbb törvényeket. Az abszolút fekete test sugárzásának törvényeit a 19. század fizikusai kísérletileg igen részletesen tanulmányozták, a legfontosabb eredmények:
Az abszolút fekete test az, melynek az abszorpciós és emissziós koefficiense minden hullámhosszra egységnyi.
Kísérletileg megvalósítható az 1. ábrán mutatott elrendezéssel: egy zárt üregen egy kis nyílást elhelyezve, a belépő fény elnyelődik, illetve a környezetnél magasabb T abszolút hőmérsékletre melegítve a kilépő fény intenzitása arányos az üregben lévő energiasűrűséggel.
A sugárzás energiasűrűségének spektrális eloszlása az 1. ábra szemlélteti. Látható, hogy a spektrális sávszélesség igen nagy, és a görbének egy maximuma van. A maximum helye fordítva arányos az abszolút hőmérséklettel (Wien-féle eltolódási törvény), így a hőmérséklet növelésével a rövidebb hullámhossz felé tolódik el.
A kisugárzott fényenergia nagysága arányos az abszolút hőmérséklet negyedik hatványával (Stefan-Boltzman-féle törvény).
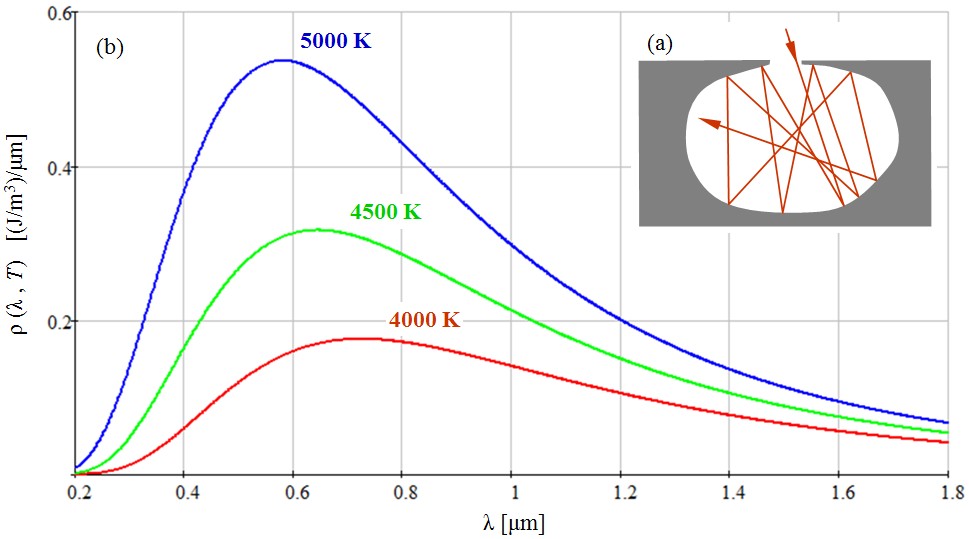
1.1. ábra. Az abszolút fekete test kísérleti megvalósítása (a), a sugárzás energiasűrűségének spektrális eloszlása 4000 K, 4500 K és 5000 K hőmérsékleten (b).
Ezen kísérleti eredményeknek az értelmezése a század legeredményesebb Maxwell-féle elektromágneses elméletével és a statisztikus fizikával az alább részletezett módon hibás eredményre vezetett.
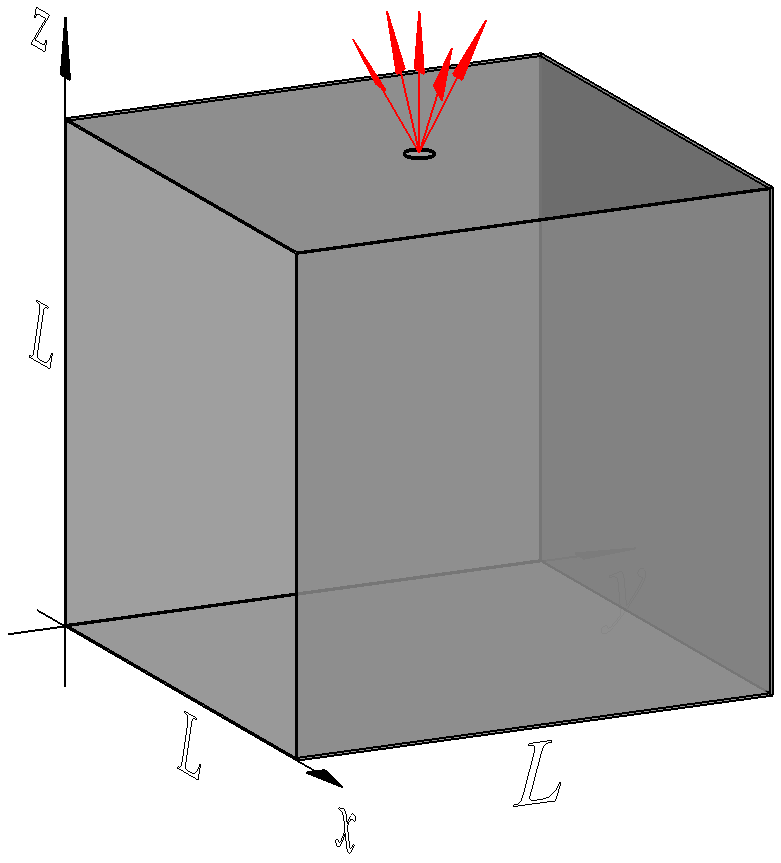
1.2. ábra. Az abszolút fekete test elméleti modellje
Legyen az előzőekben leírt abszolút fekete test egy zárt, L élhosszúságú kocka alakú fém doboz (2. ábra). A doboz belsejében stacionárius esetben a falakról való visszaverődés következtében állóhullámok alakulnak ki, ezek a zárt üreg módusai. Ha kiszámítjuk a módusok sűrűségét egy adott ν frekvenciára és megszorozzuk az egy módusra jutó energiával megkapjuk az energiasűrűséget a frekvencia függvényében. Az üregben kialakuló hullámoknak ki kell elégíteni a Maxwell egyenletekből származtatott
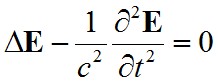 |
(1.1) |
hullámegyenletet ahol E(x, y, z, t) az elektromos térerősség vektora amely a helynek és időnek a függvénye lehet, Δ a Laplace-operátor, c pedig a fény sebessége az üregben. Ráadásul ki kell elégíteni minden falon az
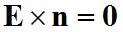 |
(1.2) |
határfeltételt is, ahol n az adott falra merőleges egységvektor. Amint az jól ismert, a változók szétválasztásával
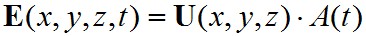 |
(1.3) |
alakú megoldást feltételezve, visszahelyettesítéssel a térfüggő tényezőre a
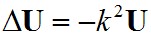 |
(1.4) |
u.n. Helmholtz-egyenlet adódik, míg az időfüggő tényezőnek a
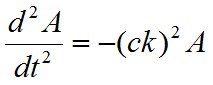 |
(1.5) |
közönséges differenciálegyenletet kell kielégítenie, ahol k egy konstans. Az időfüggő (1.5) egyenlet a jól ismert harmonikus rezgés differenciálegyenlete, így a megoldása:
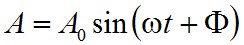 |
, | (1.6) |
ahol A0 és Φ a kezdeti feltételek által meghatározott állandók, míg ω = c·k. Ez jelenti az adott konstans amplitúdójú módusát az üregnek.
A Helmholtz-egyenletnek az U = Uxex + Uyey + Uzez megoldását szintén a változók szeparálásával határozhatók meg, ahol ex , ey és ez rendre az x, y és z tengelyek irányába mutató normált bázisvektorokat jelölik. Könnyen megmutatható, hogy
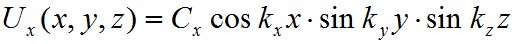 |
, | (1.7) |
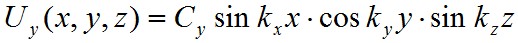 |
. | (1.8) |
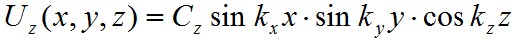 |
(1.9) |
komponensekkel adott U az (1.4) Helmholz-egyenlet megoldása, ha
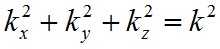 |
, | (1.10) |
és Cx, Cy és Cz állandók, továbbá kielégíti az x = 0, y = 0, és a z = 0 síkokban az előírt határfeltételeket is. A határfeltételeknek az üreg szemben lévő falain is teljesülniük kell, ezért a kx, ky és kz értékeknek teljesíteniük kell a következő összefüggéseket:
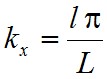 |
, | (1.11) |
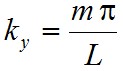 |
, | (1.12) |
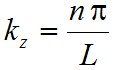 |
, | (1.13) |
ahol l, m, n pozitív egész számok. Fizikailag ezek jelentése az, hogy az x, y, z tengely irányában hány csomópontja esik az adott módusnak. Egy adott (l, m, n) számhármas meghatározza kx = kx(l), ky = ky(m) és kz = kz(n) értékeket, és így az
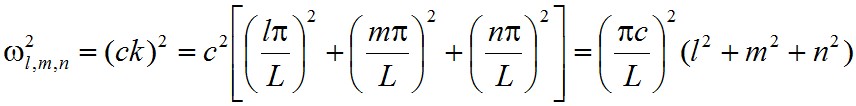 |
, | (1.14) |
adott indexekkel jellemzett módus körfrekvenciáját. A divE = 0 Maxwell-egyenlet miatt teljesülnie kell a
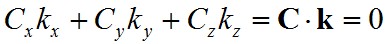 |
, |
ahol C a (Cx, Cy, Cz ) és k a (kx, ky, kz ) komponensekkel definiált vektorok. Mivel a két vektor skaláris szorzata zéus, k és C egymásra merőleges vektor. Az (l, m, n) egész számokkal definiált k és C merőlegessége csak akkor teljesül, ha C a k-ra merőleges síkban van, azaz két független komponense lehet. Számoljuk meg a lehetséges módusok számát 0 és ν között. Ezek száma megegyezik azon módusok számával melyeknek k vektorának nagysága 0 és 2πν/ c közé esik.
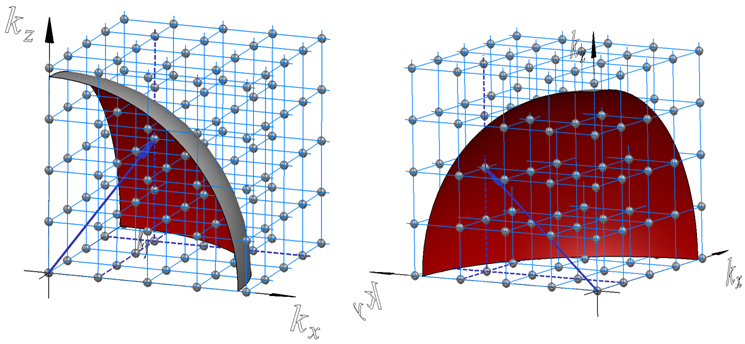
1.3. ábra. A módusokhoz rendelt rácspontok szemléltetése a (kx, ky, kz ) koordináta rendszerben, két különböző nézetből. Az (l, m, n) rendezett egészszám-hármassal jellemzett modusnak a k-térben egy rácspont feleltethető meg. Az (1, 3, 2) hármassal adott k vektort sötétkék nyíl szemléltet. Mivel minden rácspont 8 cellával érintkezik, és egy cellának szintén 8 csúcspontja van, így minden rácsponthoz kölcsönösen egy cella rendelhető. Ezért, ha a polarizációt is figyelembe vesszük, akkor módusok száma egyenlő a cellák számának a kétszeresével. Így a 0 és 2πν/c = 2π/λ közötti nagyságú k vektorral rendelkező módusok száma - jó közelítéssel - egyenlő a 2πν/c sugarú gömb-nyolcad térfogatának és a cellatérfogat hányadosának kétszeresével. Az ábrán a gömb belső felszíne vörös, a külső felszíne szürke színnel van jelölve.
Az 1.3. ábrán látható a derékszögű (kx, ky, kz ) koordinátarendszerben a lehetséges módusok által kijelölt pontok által alkotott térbeli rács. Miután kx, ky, kz mindegyike pozitív, így csak a pozitív térnyolcadba eső pontokat kell számításba venni. Ezen pontok száma 1/8-a a 2πν/c sugarú gömbnek és a π/L, π/L, π/L egységcella térfogatának a hányadosa, miután minden k-hoz 2 módus tartozhat, a módusok száma
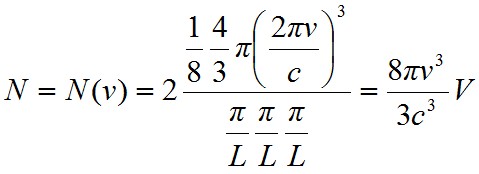 |
, | (1.15) |
ahol V = L3 az üreg térfogata. Definiáljuk a p(ν) mennyiséget mint az egységnyi térfogatba, egységnyi frekvencia tartományba eső módusok számát, melyet így a
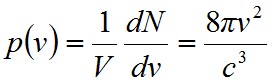 |
. | (1.16) |
formulával számolhatunk ki. Most már a módusokra jutó energiasűrűséget is ki lehet számítani egyszerűen a módussűrűséget össze kell szorozni az egy módusra jutó energiával. A statisztikus fizika igazolta, hogy a T abszolút hőmérsékletű rendszerben egy szabadsági fokra kT/2 energia jut, k a Boltzman-féle állandó. Vagyis az energiasűrűség
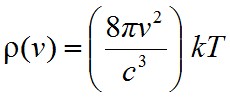 |
, | (1.17) |
ami a Rayleigh-Jeans-féle törvény néven ismert.
Az eredményre ránézve azonnal látszik, hogy a frekvencia növelésével ez egy minden határon túl monoton növekvő függvény, nincs maximuma, tehát a kísérleti eredmények leírására nem alkalmas (hullámhosszban számolva az ultraibolya tartományban tart a végtelenhez, ezért nevezték "ultraibolya katasztrófának"). A probléma megoldása Max Planck nevéhez fűződik, aki feltételezte, hogy a ν frekvenciájú módus energiája nem lehet tetszőleges, hanem csak egy hν érték (az u.n. hatáskvantum) többszöröse. Ez a feltételezés rendkívüli újdonságot jelent, hiszen a klasszikus fizika a jelenségek leírására mindig folytonos függvényeket használt, itt pedig egy kvantált mennyiség bevezetése történt.
Határozzuk meg az egy oszcillátorra jutó átlagos energiát. Legyen N megkülönböztethető részecske, a statisztikus fizika szerint hőmérsékleti egyensúlyban T hőmérsékleten átlagosan
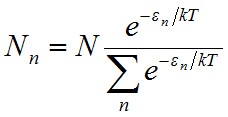 |
(1.18) |
számú részecskének van εn = nhν energiája. Így a teljes energia
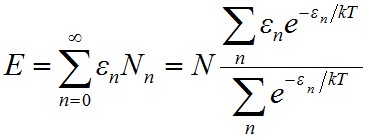 |
. | (1.19) |
Amiből az egy részecskére jutó átlagos energia
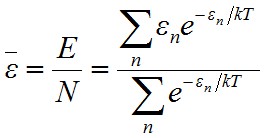 |
. | (1.20) |
Felhasználva azt, hogy a nevező egy végtelen mértani sor, valamint a számláló ennek az 1/kT szerinti deriváltja, ezért
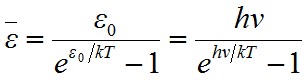 |
. | (1.21) |
Az energiasűrűséget az átlagos energiának és a módussűrűség szorzata adja, azaz
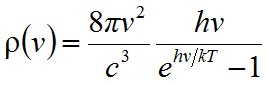 |
, | (1.22) |
ami a Planck-féle sugárzási törvény, és a kísérleti adatokkal tökéletes egyezést mutat. A csatolt interaktív szimuláció a fekete test sugárzás spektrális eloszlásának a hőmérséklettől való függését szemlélteti. A hőmérséklet csúszkával állítható, a koordinátarendszer tengelyei a "+" és "-" gombokkal skálázhatók.
Az itt leirt modell független az anyagi minőségtől, az üregben lehet vákuum, de akármilyen gáz is. Az atomfizika korán megmutatta, hogy a fény elnyelése az atom alapállapotból gerjesztett állapotba jutásával jár, míg az emisszió az alapállapotba való visszajutás eredménye. Az üregben lévő gázban tehát abszorpciós és emissziós átmenetek jönnek létre, ugyanakkor kívülről nézve ennek semmi jele. Ennek a problémának a megoldását írta le Einstein 1917-ben publikált dolgozatában.
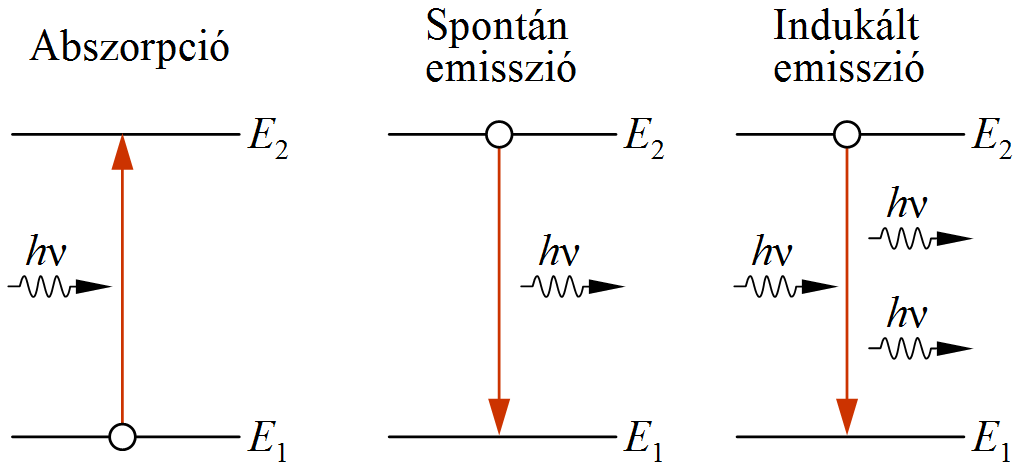
1.4. ábra. Egy kétállapotú rendszer lehetséges átmenetei.
Legyen egy zárt üreg gázzal töltve. A T abszolút hőmérsékletű stacionárius állapotban a gáz a 1.4. ábrán E1 energiájú alap és E2 energiájú gerjesztett állapotokkal rendelkezzék az abszorpció és emisszió E2 - E1= hν energiájú foton elnyelését, illetve kisugárzását jelenti. Legyen az alapállapotok sűrűsége n1 , a gerjesztett állapotoké n2 , a részecskék száma állandó, azaz n = n1 + n2. Vizsgáljuk meg a lejátszódó elemi jelenségeket, és ezek gyakoriságát. Amint az előbb leírtuk az abszorpció az alapállapotból a gerjesztett állapotba való átmenetet jelenti, egy abszorpciós aktus n1 értékét 1-gyel csökkenti. Kézenfekvő az feltételezés, hogy egy kicsiny dt idő alatt egységnyi térfogatban elnyelt fotonok száma (n1 változása) arányos a dt idővel, az alapállapotú atomok n1 számával és elektromágneses tér energiasűrűségének spektrális sűrűségével, ρ(ν)-vel, azaz
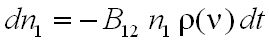 |
, | (1.23) |
ahol B12 az anyagra jellemző állandó, az úgynevezett abszorpciós Einstein-féle koefficiens. A gerjesztett állapotú részecskék sugárzással visszamennek az alapállapotba, aminek két módja lehetséges. Az egyik során a részecske minden külső hatás nélkül megy vissza alapállapotba (ez az energia minimum). Becsüljük meg ezek számát tudva azt, hogy minden kisugárzott foton 1-gyel csökkenti n2 számát. Szintén plauzibilis az a feltevés, hogy a kicsiny dt idő alatt egységnyi térfogatban kisugárzott fotonok száma (n2 változása) arányos a dt időtartammal, az gerjesztett állapotú atomok n2 számával, vagyis
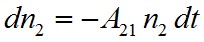 |
, | (1.24) |
ahol A21 az anyagra jellemző állandó, az úgynevezett spontán emissziós Einstein-féle koefficiens. A21 fizikai jelentését könnyen megadhatjuk, hiszen a fenti egyenletet az
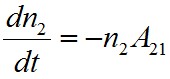 |
. | (1.25) |
differenciálegyenletetre vezet, melynek a t = 0 időpontbeli n20 = n2(0) kezdőfeltételhez tartozó megoldása
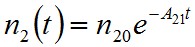 |
, | (1.26) |
ami azt mutatja, hogy az emisszió miatt a gerjesztett atomok száma exponenciálisan csökken. Bezetve a τ = 1/A21 jelölést (1.26) egyenlet
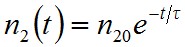 |
(1.27) |
alakba írható, amely jól mutatja a τ mennyiség jelentését, hiszen a t = τ időpillanatban
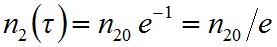 |
. | (1.28) |
Vagyis τ megadja azt az időtartamot, amely alatt a gerjesztett állapotok száma e-ad részére esik, ezért τ-t a gerjesztett állapot átlagos élettartamának nevezzük.
Szimmetria okokból és analógia alapján Einstein feltételezte, hogy a gerjesztett állapot a rezonancia miatt a ν frekvenciájú sugárzás hatására visszamegy alapállapotba miközben a kényszerítő sugárzással azonos irányú, frekvenciájú, polarizációjú, fázisú sugárzást bocsát ki, és ezt nevezte kényszerített emissziónak. Ezek száma a fentiekkel analóg módon
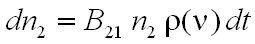 |
, | (1.29) |
ahol B21 a kényszerített emisszió Einstein-féle koefficiense, ρ(ν) az emissziót indukáló elektromágneses hullám spektrális-energiasűrűsége (azaz az energiasűrűség spektrális sűrűsége).
Mindhárom lehetséges átmenetet figyelembe véve a gerjesztett nívó betöltésének változását a
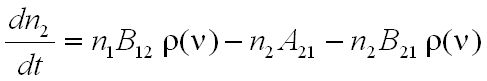 |
(1.30a) |
differenciálegyenlet írja le, ahol az első tag az abszorpció, a második tag a spontán emisszió míg a harmadik tag pedig az indukált emisszió következtében létrejövő változást írja le.
A T hőmérsékletű üregben természetesen ν frekvenciájú sugárzás is jelen van, tehát abszorpciós átmenetek is létrejönnek. Kísérletileg, azonban ν frekvenciájú sugárzás hiányának nyoma sincsen. Ez csak úgy lehetséges, hogy ha dinamikus egyensúly áll fenn, tehát ha az abszorpciós és emissziós átmenetek száma megegyezik egymással, vagyis n2 időben nem változik, azaz dn2/dt = 0, így az előző egyenlet alapján
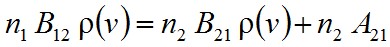 |
. | (1.30b) |
A statisztikus fizikából ismert, hogy hőmérsékleti egyensúlyban az egyes állapotok populációjára az
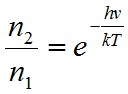 |
(1.31) |
összefüggés áll fenn. (1.30) egyenletből az n2/n1 hányadosra
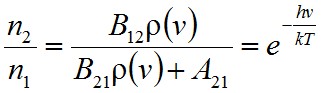 |
(1.32) |
adódik. Ebből fejezzük ki ρ-t, és hasonlítsuk össze a Planck-féle sugárzási törvénnyel:
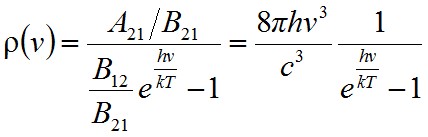 |
. | (1.33) |
Látható, hogy az egyenlet két oldalán két igen hasonló kifejezés áll. Az egyenlőség csak akkor állhat fenn, ha
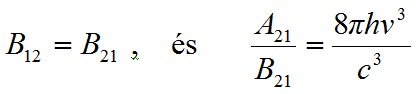 |
. | (1.34) |
Ezzel megmutattuk az Einstein-féle koefficiensek közötti összefüggéseket. Azt a meglepő eredményt kaptuk, hogy B12 = B21, tehát a két kényszerített átmenetet leíró anyagi jellemző egyenlő egymással. A másik kifejezésnek is fontos jelentést adhatunk egy kis átalakítással:
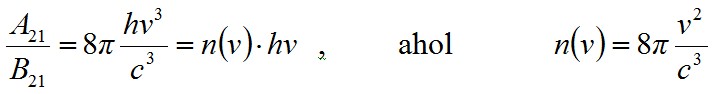 |
a módusok száma. Ebből az
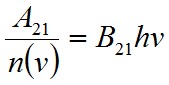 |
. | (1.35) |
eredményhez jutunk, ami azt mutatja, hogy az egy módusra eső spontán emisszió egyenlő az egy foton által keltett indukált emisszióval (ez a látható tartományban szobahőmérsékleten 10-10 nagyságrendű).
Az itt bemutatott modell számos nem elhanyagolható egyszerűsítést tartalmaz, ám gyakorlati célokra alkalmas formára is hozhatók az eredményei az alábbiak szerint. A modell minden állapothoz véges élettartamot rendel hozzá, aminek következtében véges hosszúságú hullámokat nyel el, vagy bocsát ki a részecske (ami a kísérleti tapasztalatokkal egybeesik). A Heisenberg-féle határozatlansági relációknak (vagy a Fourier-transzformációnak) megfelelően a véges hosszhoz tartozó energia véges bizonytalansággal rendelkezik, azaz
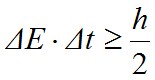 |
. | (1.36) |
Az E = hν miatt a sugárzás nem monokromatikus, azaz véges sávszélességű és hosszúságú, mivel a monokromatikus sugárzáshoz végtelen hossz tartozna. Az 1.5. ábrán látható véges energia bizonytalanságú (azaz véges élettartamú) energiaszintekkel bíró rendszernél az 1 és 2 állapotok energiaeloszlás-csúcsainak távolsága E2 - E1 = hν21. Egy adott ν frekvenciájú sugárzás egymástól hν távolságra lévő energiaszintek közötti átmenet során jön létre. A véges energia bizonytalanság miatt ez sokféleképpen valósulhat meg. Például a ν21 frekvenciájú sugárzás jön létre a három zöld nyíllal jelölt esetekben. A nívókat felfelé, vagy lefelé azonos távolságra eltolva, a sugárzás frekvenciája nem változik, mert a nívók közötti távolság ugyanaz marad. Nyílván azok az átmenetek a leginkább valószínűek, amikor a felső és az alsó nívók energiája olyan helyen van, ahol az eloszlásfüggvényük nagy értékkel bír. A véges sávszélességű nívók közötti átmenet révén létrejövő sugárzás spektrális eloszlását az u.n. g(ν) vonalalak függvénnyel jellemezhetjük, melynek az értelmezése a következő: Annak a valószínűsége, hogy a nívók közötti átmenet során a kibocsátott vagy elnyelt sugárzás frekvenciája a ν frekvencia körüli kicsiny dν frekvenciasávba esik, definíció szerint, g(ν)·dν. Ez alapján g(ν) egy valószínűségi sűrűség, és mivel a sugárzás frekvenciája biztosan benne van a (0, ∞) tartományban, így
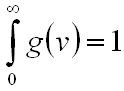 |
. | (1.37) |
Mivel az 1 és 2 állapotok energiaeloszlás-csúcsainak távolsága hν21, a felső és alsó nívókat azonos módon fel vagy lefelé mozgatva, a felső és az alsó energiaértékek egyszerre esnek az eloszlásuk nagyobb értékére, a ν21 frekvenciájú sugárzás a leginkább valószínű. Ezért a g(ν) függvény maximuma a ν21 frekvenciánál lesz. A frekvencia értékét csökkentve (pl. ν = ν-), vagy növelve (pl. ν = ν+) a nívók távolsága csökken, vagy nő. Mindkét esetben a felső és alsó nívókat azonos módon fel, vagy lefelé mozgatva, a felső és az alsó energiaértékek nem esnek egyszerre az eloszlásuk nagyobb értékére, melynek következtében az ilyen átmenetek kevésbé valószínűek. Amiért a frekvenciát a ν21-től csökkentve, vagy növelve a g(ν) vonalalak függvény csökken.
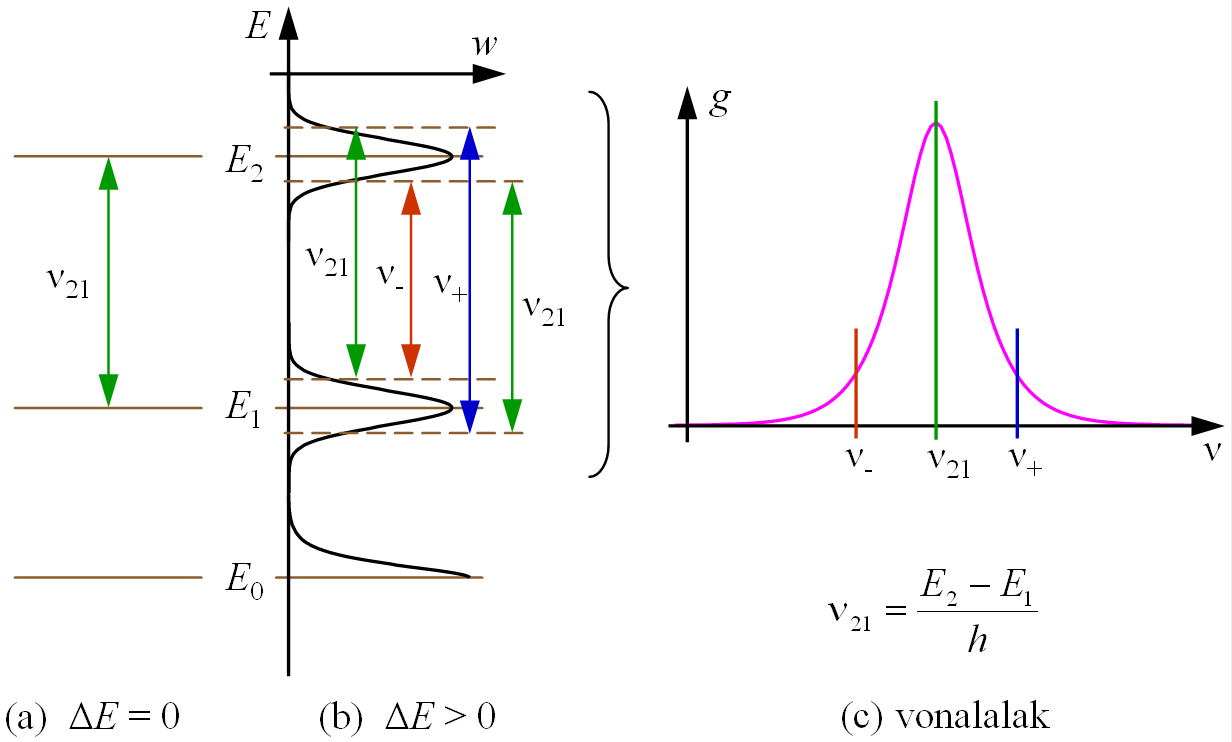
1.5. ábra. A vonalalak függvény értelmezése.
A vonalalak függvény felhasználásával a gerjesztett nívó betöltésének időbeli változását a
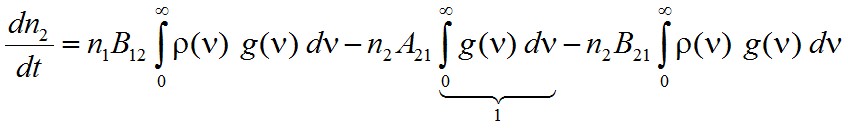 |
differenciálegyenlet írja le, ahol az első tag az abszorpció, a második tag a spontán emisszió míg a harmadik tag pedig az indukált emisszió következtében létrejövő változást írja le. Amennyiben a ρ(ν) spektrális szélessége sokkal nagyobb, mint a g(ν) spektrális szélessége, akkor a ρ(ν) az integrálás során állandónak tekinthető, és így az
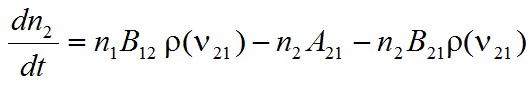 |
egyenletre vezet, ami formailag azonos az eredeti Einstein-féle leírással (lásd az (1.30a) egyenletet). A másik szélsőséges eset az amikor a ρ(ν) spektrális szélessége sokkal kisebb, mint a g(ν) spektrális szélessége, azaz a sugárzás gyakorlatilag egy ν0 frekvenciájú monokromatikus hullám. Ekkor a spektrális-energiasűrűség a
 |
. |
formula adható meg, ahol ρ0 a monokromatikus hullám energiasűrűsége és δ(ν) Dirac-féle függvény. Ekkor a gerjesztett nívó betöltésének időbeli változását a
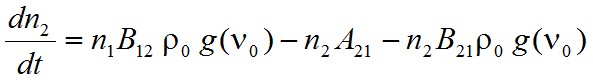 |
egyenlet írja le. Ami azt mutatja, hogy ha B12 és a B21 együtthatóknak megfeleltetjük a B12 g(ν0) és a B21 g(ν0) kifejezéseket, akkor formailag megint az eredeti Einstein-féle leírást kapjuk. Érdemes megjegyezni, hogy ekkor az egyenletben nem Js/m3 dimenziójú spektrális-energiasűrűség (ρ(ν)), hanem a J/m3 dimenziójú (a teljes frekvenciatartományra vonatkozó) energiasűrűség (ρ0) szerepel. A vonalalak (vonalkiszélesedés) fizikai eredetéről és fajtáiról a későbbiekben a 2. fejezetben részletesen lesz szó.
Az előbbi modell egy termikus egyensúlyban lévő üregben kialakuló állóhullámok elnyelésével és emissziójával számol, a gyakorlatban pedig többnyire egy fényforrásból kilépő fényteljesítmény elnyelődését lehet, illetve kell meghatározni. Az anyagok fényelnyelésének gyakorlati jellemzésére alkalmas fogalom a hatáskeresztmetszet, amit az 1.6. ábrán látható modellel alábbi egyszerű gondolatmenettel lehet bevezetni.
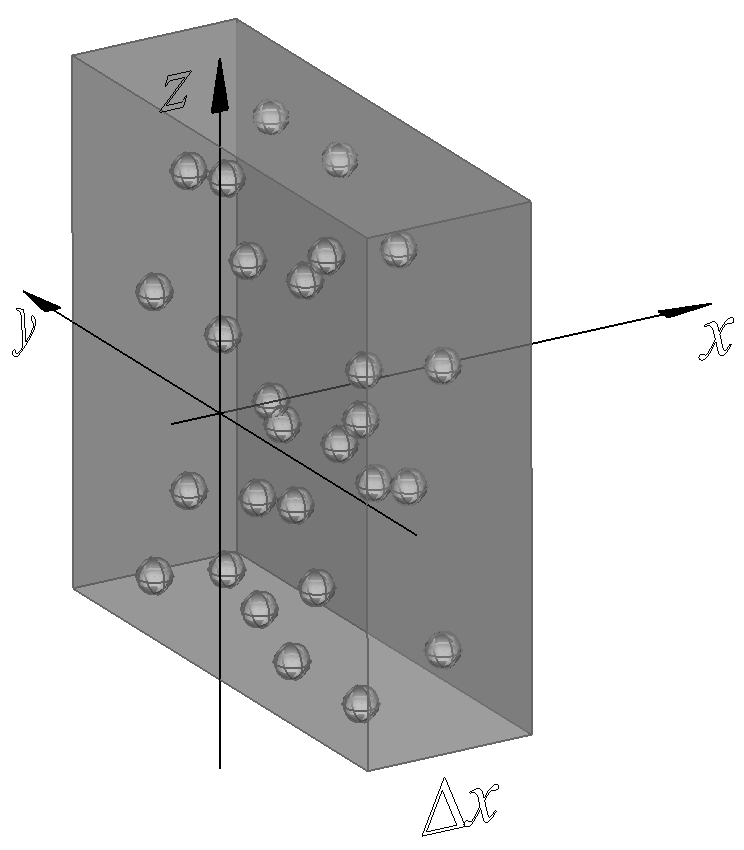
1.6. ábra. A hatáskeresztmetszet modellje.
Essen egy P teljesítményű A keresztmetszetű fénynyaláb egy kicsiny dx vastagságú anyagra, amiben egy kicsi σ méretű fekete folt van. Az intenzitás az I = P/A módon definiálható, a teljesítmény változása pedig dP = -(σ/A)·P, ahol a negatív előjel arra utal, hogy az elnyelés miatt csökkenésről van szó. Ha nem egy, hanem N sűrűségű folt van, akkor N·dx·A darab van, ami σ·N·dx·A felületet takar ki. Ekkor a teljesítmény változás
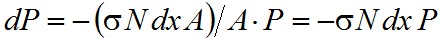 |
. | (1.38) |
Mindkét oldalt A-val osztva:
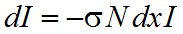 |
. | (1.39) |
Bevezetve a k = σN mennyisséget, az abszorpció törvény differenciális alakját kapjuk:
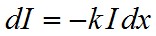 |
, | (1.40) |
aminek a szokásos megoldása
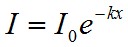 |
, | (1.41) |
ahol I0 az anyagra beeső intenzitás I pedig a kimenő intenzitás. Tehát a σ hatáskeresztmetszet a részecskékre jellemző állandó, az egy részecske abszorpciójával ekvivalens abszolút fekete folt területe, mértékegysége cm2.
Az egyébként szintén a részecske elnyelését jellemző B12-vel a σ = hν B12/c összefüggésben van. Végül a gyakorlati célokra alkalmas formája a véges sávszélesség figyelembe vételével:
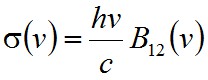 |
, | (1.42) |
és az Einstein koefficiensek közötti összefüggésre gondolva: σa = σe. A továbbiakban a σ, ha nincs is jelölve, frekvencia vagy hullámhosszfüggőnek tekintendő.
Az eddigi ismereteink alapján az előzőekben bevezetett abszorpciós törvényt újra kell gondolnunk, hiszen most már tudjuk, hogy a kényszerített abszorpciós és emissziós hatáskeresztmetszet egyenlő egymással. Az előzőekben bevezetett jelölésekkel az I intenzitású fény intenzitásának változása:
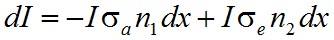 |
, | (1.43) |
ahol n1, n2 az alap és gerjesztett állapot sűrűsége, dx a rétegvastagság. Átrendezve
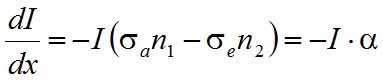 |
. | (1.44) |
Ami igen hasonló az előzőekben levezetett elnyelési törvényhez, a különbség mindössze annyi, hogy itt a k helyett egy zárójeles kifejezés van. Miután a zárójelben lévő kifejezés egy különbség, aminek az előjele lehet pozitív vagy negatív, így a dI lehet pozitív vagy negatív is. Más szóval az intenzitás csökkenhet, vagy nőhet. Ami azt jelenti, hogy a fény gyengítése, és erősítése is felléphet. Ez teljesen új eddig nem tárgyalt jelenség! Az (1.44) egyenlet alapján az erősítés feltétele
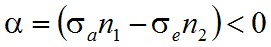 |
. | (1.45) |
Amiből - figyelembe véve, hogy σa = σe az erősítés feltételére az
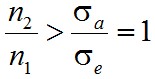 |
(1.46) |
feltételt kapjuk. Ez pedig azt jelenti, hogy ha a gerjesztett állapot sűrűsége nagyobb, mint az alapállapoté, erősítés lép fel. Visszagondolva a statisztikus fizika már említett eredményére, stacionárius állapotban
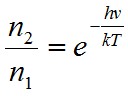 |
. | (1.47) |
Szobahőmérsékleten kT = 3 meV, a látható tartományon a hν = 3 eV, a kettő hányadosa 1000, vagyis
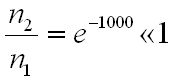 |
, |
ami gyakorlatilag 0. Az is világos, hogy amennyiben a T → ∞, a hányados alulról egyhez tart, ami annyit jelent, hogy a hőmérséklet emelésével termikus egyensúlyban populáció inverziót nem lehet létrehozni.
A gerjesztés nyilvánvalóan sokkal jobb hatásfokkal létrehozható optikai gerjesztéssel, mint melegítéssel, amikor egy foton elnyelésével egy gerjesztett állapotot lehet létrehozni. Vizsgáljuk meg közelebbről ezt az esetet is. Vegyük a korábban már definiált kétszintes rendszert, és nézzük meg, hogy mi történik az optikai gerjesztés hatására. A gerjesztett állapot populáció sűrűségének változása az abszorpció és kényszerített emisszió miatt
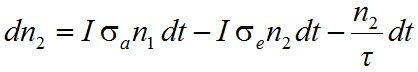 |
. | (1.48) |
Az első tag jelenti az abszorpció, a második a kényszerített emisszió hatását, a harmadik pedig a spontán emisszió miatti csökkenést. Az (1.48) egyenletből a
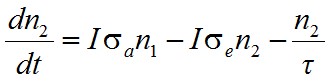 |
(1.49) |
differenciálegyenlet adódik. Tételezzük fel, hogy I állandó, és megvárjuk a stacionárius állapot kialakulását, azaz
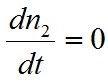 |
. |
Ekkor (1.49) egyenlet az
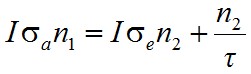 |
(1.50) |
algebrai egyenletté egyszerűsödik. Ebből n2/n1-et kifejezve
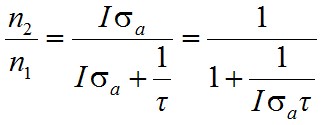 |
. | (1.51) |
kapjuk. Megvizsgálva a gerjesztő intenzitás növelésének hatását, világosan látszik, hogy ha I → ∞, akkor n2/n1 tart alulról 1-hez, tehát a populáció inverzió így sem érhető el. Ennek oka az, hogy a beeső fotonok abszorpciót és emissziót azonos valószínűséggel hoznak létre. Erre a megoldás az, hogy a gerjesztés és az erősítés szintjeit szét kell választani. Optikai gerjesztéssel populáció inverziót a 1.7. ábrán látható három, négy és kiszélesedett termsémával lehet megvalósítani.
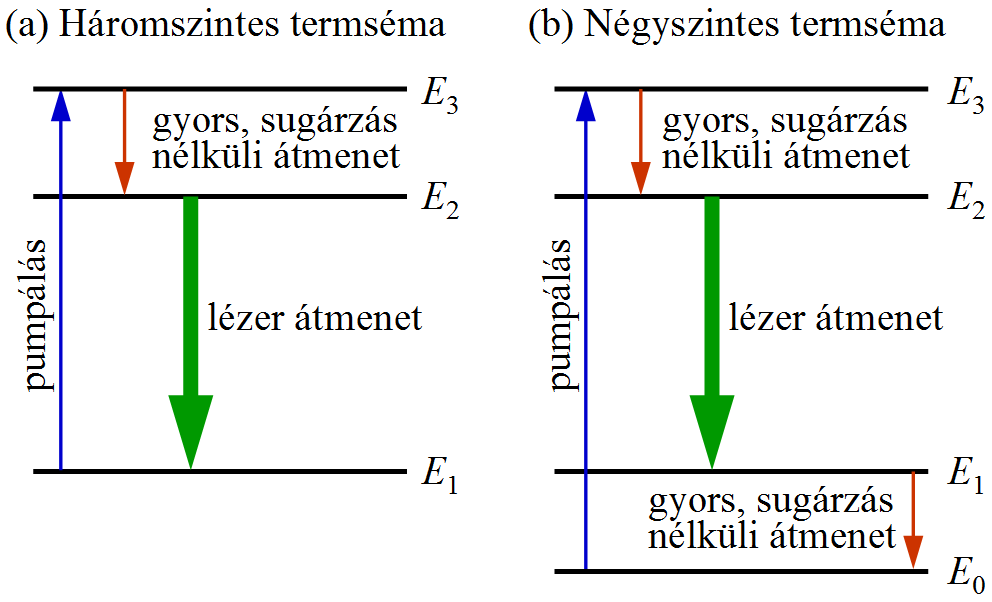
1.7. ábra. Lézerek optikai gerjesztéséhez alkalmas termsémák.
Az ábra jelöléseivel világos, hogy egy nagyobb energiájú foton elnyelése után egy gyors sugárzásnélküli átmenettel jutnak a részecskék az emisszióhoz szükséges gerjesztett állapotba. A kényszerített emisszió pedig vagy alapállapotba, vagy egy ehhez közeli átmeneti állapotba viszi a részecskéket. Az itt leírt működési vázlat két fontos dolgot mutat: egy részecske megfelelő körülmények között többször is körbefuthat az előbb leirt útvonalon, az egy körre eső energiaveszteség csökkenti a hatásfokot, illetve a sugárzásnélküli átmenetek melegítik az aktív közeget.
A populáció inverzió létrehozása más módszerekkel is lehetséges, hiszen az atomfizika számos jelenséget ismer, melynek során az atomok vagy molekulák gerjesztett állapotba kerülhetnek. Az egyik lehetséges gerjesztési módszer a megfelelő energiájú elektronütközéssel való gerjesztés. Technikailag a legtisztább megoldás egy elektrongyorsító elektronnyalábjával bombázni az aktív közeget. Az elvi egyszerűsége mellett megemlítendő, hogy általában 100-500 kV feszültségen kell 50-100 ns alatt 50-100 kA-es áramlöketet létrehozni, ami a használatukat erősen korlátozza. Lényegesen egyszerűbb technikai megoldás, ha az aktív anyag gáz halmazállapotú és az ebben létrehozott gázkisülés elektronjai ütköznek az atomokkal és molekulákkal. A gyakorlatban ez igen elterjedt, részletesen bemutatjuk a lézerek gerjesztéséről szóló fejezetben. Végül gerjesztett állapotok keletkeznek bizonyos kémiai reakciókban is, amikor a komponensek egy gerjesztett állapotú végterméket hoznak létre. Ennek az eljárásnak előnye a magas hatásfok, hátránya, hogy többnyire irreverzibilis, azaz csak egyszer használatos.
Az eddigi ismereteink alapján most már tudjuk, hogy az optikai tartományban is lehet erősítést létrehozni megfelelő feltételek teljesülése esetén. A mérnöki gyakorlatban jól ismert, hogy az elektronikában az erősítőkből oly módon lehet oszcillátort kialakítani, hogy visszacsatolást hozunk létre a bemenet és kimenet között. Logikus lépés, hogy ha az optikai tartományban tudunk erősítést kapni megfelelő visszacsatolással oszcillátort is, ez az oszcillátor a lézer. A visszacsatolás legegyszerűbb módja a 1.8. ábrán látható módon valósítható meg, egy aszimmetrikus alakú erősítő közeget két párhuzamos síktükör közé helyezünk.
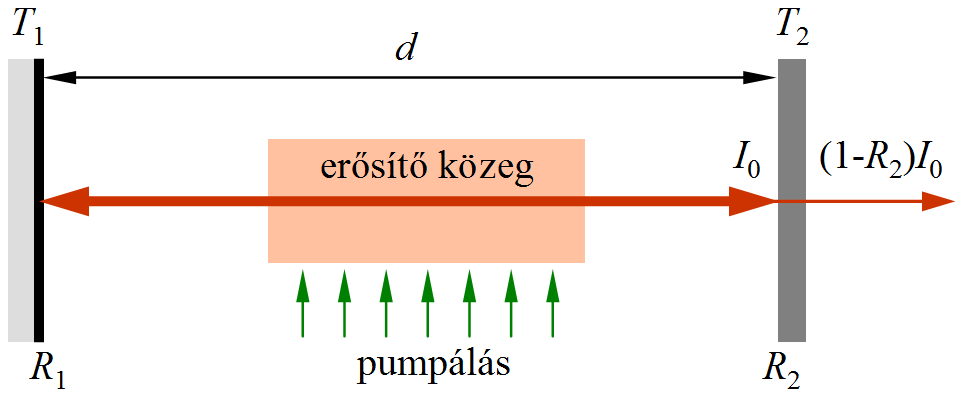
1.8. ábra. A legegyszerűbb lézer modell.
A két tükör között oda- vissza verődő fény reflexiós és egyéb veszteségeit az erősítésnek kell kompenzálnia. Ezt a tényt egy egyszerű modellel le is lehet írni, legyen az erősítő közeg l hosszúságú, benne az erősítési tényező α, a tükrök reflexiója R1 és R2. Induljon el egy I0 intenzitású nyaláb az ábrán látható módon, amely áthaladva az erősítő közegen I0·eα l -re erősödik. A jobboldali tükörről R2·I0·eα l verődik vissza, majd az erősítő közegen ismételten áthaladva, újra erősítődik (R2·I0·eα l )·eα l értékre, a baloldali tükörről végül, R1·R2·I0·e2α l verődik vissza. Ezzel visszajutottunk a kiindulási pontra. Ha azt szeretnénk, hogy egy kör megtétele után az intenzitás legalább elérje az induló értéket az I0 ≤ R1·R2·I0·e2α l feltételnek kell teljesülni. Ha ezt elértük, az oszcillátor addig működik, amíg az erősítés pótolja a veszteségeket, ez az önfenntartó működés küszöbfeltétele. Az egyenletben a lehetséges egyszerűsítést elvégezve, mindkét oldal természetes logaritmusát véve:
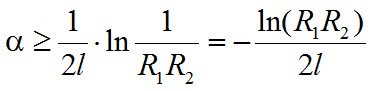 |
. | (1.52) |
Ha például, l = 1 m, R1 = 1 és R2 = 0.5 (azaz a második tükör félig áteresztő, amelynél a lézer fénye kilép a rezonátorból), akkor 0.3466/m ≤ α relációt kapjuk.
Szokásos deifiniálni a rezonátor jósági tényzőjét a
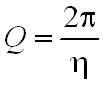 |
(1.53) |
defincióval, ahol η az egy periódus alatt bekövetkező energiavesztesség. Mivel η = α∙λ, és λ = c/ν így
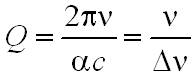 |
, | (1.54) |
ahol Δν a rezonátor erősítési görbéjének a félértékszélessége.
Az itt leírt modell alapján, képet kaphatunk a lézerek működésének elvi alapjairól, a későbbi fejezetekben pedig az itt bemutatott egyszerűnek látszó jelenségek részletes analízisét találjuk meg. A csatolt interaktív szimuláció a lézerműködést szemlélteti. A rádiógombok segítségével válaszhatunk két- vagy háromszintes modell közül, továbbá az aktív közeget tükrök közé helyezhetjük. Csúszkákkal állíthatjuk a gerjesztett állapot élettartamát, és a gerjesztő fény hullámhosszát és intenzitását, valamint a tükrök visszaverőképességét.
Fogalmazza meg a hőmérsékleti sugárzásra vonatkozó Kirchhoff-féle törvényt!
Mit értünk abszolút fekete testen?
Igazolja a Wien-féle eltolódási törvényt és a Stefan-Boltzman-féle törvényt a Planck-féle sugárzási törvényből kiindulva!
Definiálja az Einstein-féle együtthatókat! Milyen összefüggés áll fenn közöttük?
Értelmezze az abszorpciós hatáskeresztmetszetet!
Ismertesse a fejezetben bemutatott egyszerű lézer modellt!
[1.1] Budó Ágoston, Mátrai Tibor, Kísérleti fizika III. kötet. Optika és atomfizika (Tankönyvkiadó, Budapest, 1985)
[1.2] W. Demtröder, Laser Spectroscopy (Springer)
[1.3] O. Svelto: Principles of lasers (4ed., Springer, 1998)
[1.4] A.E Siegman: Lasers (University Science Books, 1986)
Tartalom
Az 1. fejezetben megvizsgáltuk az optikai erősítés kialakulásának a feltételeit és megállapítottuk, hogy a termikus egyensúlytól jelentős mértékű eltérés, vagyis populáció inverzió szükséges hozzá. Amennyiben képesek vagyunk a populációk ilyen mértékű manipulációjára, újra kell gondolnunk az abszorpció és erősítés tulajdonságait, mivel a populáció inverzió esetén az alapállapotú részecskék száma legalább a felére csökken a gerjesztés miatt, tehát az abszorpcióra képes részecskék száma legalább a felére esik ezzel együtt pedig az eredő abszorpció is csökken. Hasonló gondolatmenettel: az erősítés is változik, amennyiben egy jel erősítődik, mivel a kényszerített emissziós átmenetek pedig az erősítést csökkentik. Az itt leírt két jelenség számos gyakorlati alkalmazással rendelkezik a lézerek működésében, az impulzusok formálásában, jelek erősítésében és összefoglaló néven telítődésnek nevezzük.
Az abszorpció telítődésének tulajdonságait a 2.1. ábrán látható kétszintes modellel szemléltethetjük.
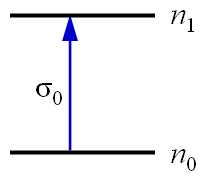
2.1. ábra. Az abszorpció telítődésének modellje.
A modell lehetővé teszi az abszorpciós és emissziós jelenségek szétválasztását. A korábban is alkalmazott jelölésekkel n0 az alapállapotú részecskék koncentrációja, n1 a gerjesztett állapotoké, és mivel a részecskék száma állandó: n0 + n1 = n. A gerjesztett állapotú részecskék számának a változását a
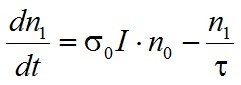 |
(2.1) |
differenciálegyenlet írja le, melyből az n0-t kiküszöbölve n1 időbeli változását a
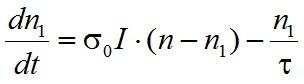 |
(2.2) |
differenciálegyenlet határozza meg. Ez az egyenlet az esetek többségében csak numerikusan oldható meg, de alapvető információk nyerhetők, ha az I(t) függvényt egy a 2.2. ábrán látható I0 nagyságú ugrásfüggvénynek (a) vesszük fel. Ez az eljárás a mérnöki gyakorlatban igen elterjedt.
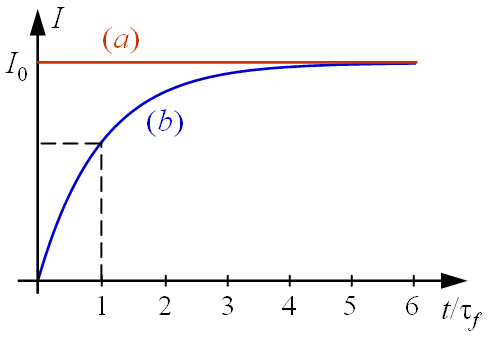
2.2. ábra. A beeső fény intenzitásának időfüggését [(a) görbe] egy I0 nagyságú ugrásfüggvény írja le. A gerjesztett állapotban lévő részecskék sűrűségének változását a (b) görbe mutatja.
A (2.2) differenciálegyenlet erre az esetre vonatkozó megoldása, mint az visszahelyettesítéssel könnyen igazolható,
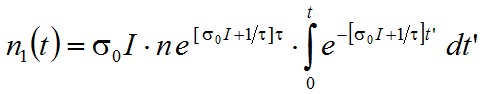 |
, | (2.3) |
amiből az integrálást elvégezve:
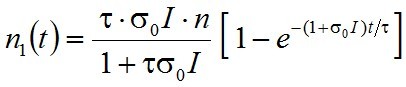 |
. | (2.4) |
Mint látható, számos helyen azonos mennyiség, a τσ0 fordul elő. Vezessük be az It = 1/( τσ0) jelölést, az u.n. telítési intenzitást, valamint az exponensben definiáljuk a
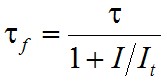 |
, | (2.5) |
mennyiséget, amellyel az n1(t) függvény
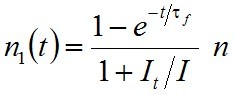 |
, | (2.6) |
alakú lesz. A számlálóban lévő kifejezés biztosítja a válaszfüggvény exponenciálisan felfutó alakját, ami a 2.2 (b) ábrán látható. Vizsgáljuk meg a felfutási idő tulajdonságait, hiszen mint látjuk függ I-től és It-től is. Három érdekes eset van:
ha I « It , akkor τ f = τ tehát a felfutási idő egyenlő a gerjesztett állapot élettartamával,
ha I = It , akkor a τ f = τ/2 , így a felfutási idő felére csökkent, míg
ha I » It , akkor τ f → 0, azaz a felfutási idő nullához tart.
Tehát, olyan érdekes eredmény adódott, hogy a válaszfüggvény felfutási ideje intenzitásfüggő, és a telítési intenzitás pedig nem más, mint azon intenzitás, amelynél az eredeti felfutási idő a felére csökken.
További fontos következtetéseket vonhatunk le, ha az itt kapott megoldásfüggvényt megvizsgáljuk, hogy milyen lesz, ha t nagyon nagy. Ebben az esetben az n1(t) függvényben a zárójelben lévő kifejezés egyhez tart, tehát konstans értékhez tart:
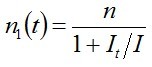 |
. | (2.7) |
Figyelembe véve a részecskék megmaradásának elvét (azaz az n0 = n - n1 összefüggést),
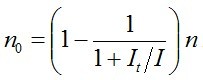 |
. | (2.8) |
Ebből látható, hogy n0 értéke intenzitásfüggővé válik, amelyben az It telítési intenzitásnak ismét fontos szerepe van. Írjuk fel ismét az abszorpció törvényét differenciális alakban:
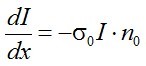 |
. | (2.9) |
Az n0 helyére beírjuk az itt kapott (2.8) intenzitásfüggő kifejezést és kapjuk, hogy
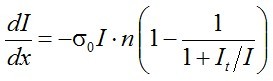 |
, | (2.10) |
amiből világosan látszik, hogy az abszorpció törvénye most már függ az intenzitástól is. Vizsgáljuk meg a különböző speciális eseteket:
ha I « It , akkor dI/dx = -σ0 I n, amely az abszorpció klasszikus esete,
ha I = It , akkor dI/dx = - σ0 I n/2, ami azt mutatja, hogy az abszorpció a felére esik,
ha I » It , akkor dI/dx → 0, vagyis az abszorpció nullához tart.
Ezt a jelenséget, vagyis amikor nagy gerjesztő intenzitáson az abszorpció nullához tart, vagyis átlátszóvá válik az anyag, az abszorpció telítődésének, vagy kifakulásának nevezzük. Itt csak a legegyszerűbb megoldásait vizsgáltuk az abszorpció differenciálegyenletének. Ha az I(t) függvény nem ilyen egyszerű függvény (a gyakorlatban ez többnyire így van), az egyenlet megoldása csak numerikusan lehetséges. A telítődésnek, a telítődő abszorbenseknek számos gyakorlati alkalmazása van a lézerek fizikájában elsősorban impulzusok alakjának formálására, rövidítésére használják, valamint erősítő fokozatok elválasztására.
Az abszorpció telítődésének tulajdonságai további érdekes alkalmazásokat tesznek lehetővé, ha nem kétszintes termsémát vizsgálunk, hanem bonyolultabb rendszereket. Tekintsünk egy a 2.3. ábrán látható háromszintes sémát, amelynél az egyes állapotok távolsága egyenlő, a betöltöttségének a koncentrációja legyen rendre n0, n1 és n2, továbbá a 2. állapot élettartama legyen nagyon rövid (1 ps nagyságrendű), az abszorpciós hatáskeresztmetszetek σ0 és σ1.
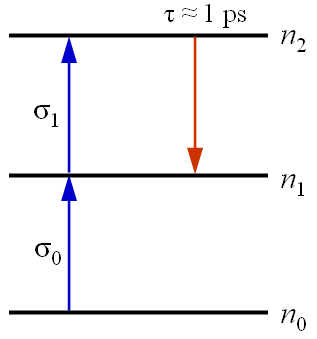
2.3. ábra. Egyszerűsített háromszintes modell az abszorpció modellezéséhez.
Mivel a 2. állapot élettartama igen kicsiny, a részecskék egy n1 → n2 átmenet után is az azonnal újra az 1. állapotba kerülnek, vagyis n2 = 0, így az n1 populáció koncentrációjának változását meghatározó egyenlet egyszerűen
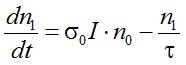 |
. | (2.11) |
Ha I állandó, akkor elegendően sok időt várva kialakul a stacionárius eset, melyet a dn1/dt = 0 feltétel jellemez. Ezzel a kikötéssel a (2.11) egyenlet egyszerű algebrai egyenletté válik. Felhasználva n0 = n - n1 összefüggést, a megoldása
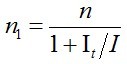 |
, |
ugyanúgy, mint a kétszintes esetben. Az abszorpció differenciálegyenlete ekkor
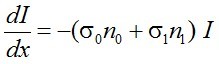 |
, | (2.12) |
megint figyelembe véve, hogy n0 = n - n1 ,
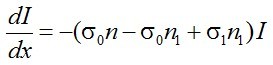 |
(2.13) |
adódik. Az n1 helyére a kiszámolt stacionárius kifejezést beírva, a
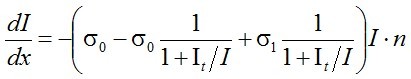 |
. | (2.14) |
formulát kapjuk, melyet átalakítva, a
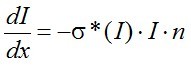 |
. | (2.15) |
alakba írhatunk fel, ahol σ* a zárójelben lévő tényezőt jelöli. Tegyük fel az I igen kicsiny, ekkor a zárójelben a két telítődő tag elhanyagolható és az abszorpció klasszikus egyenletét kapjuk vissza. Legyen I = It , ekkor a zárójelben a telítődő tagok 1/2-del egyenlők.
Ekkor viszont több eset lehetséges:
Ha σ0 = σ1, a két utolsó tag egyenlő egymással és eredője nulla, vagyis olyan abszorberünk van, amelynek elnyelése minden intenzitáson ugyanannyi.
Ha σ0 > σ1, a két kifejezés eredője negatív, tehát a zárójeles kifejezés csökken, tehát a kifakulás esete áll fenn.
Ha σ0 < σ1, az eredő pozitív, tehát a zárójeles kifejezés nőtt, ami azt jelenti, hogy az abszorpció növekedett, vagyis elsötétül.
Amennyiben I sokkal nagyobb, mint It , a két telítődő tag 1-hez tart és az eredmény ismét σ-tól függ ugyanúgy, mint az előbb. Látható tehát hogy többszintes anyagok alkalmazásával megfelelő paraméterek választásával igen eltérő intenzitásfüggő abszorpció nyerhető.
A gerjesztett állapotok száma nem csak az abszorpciót csökkenti, hanem populáció inverzió esetén erősítést tesz lehetővé. Ha jelet erősítünk, a nagy számú kényszerített emisszióval viszont csökkentjük a gerjesztett állapotokat, ezen keresztül pedig az erősítést. Ez a jelenség az erősítés telítődése. A (2.1) egyenlet kis kiegészítéssel, figyelembe véve a kényszerített emissziót is, alkalmas az erősítés telítődésének leírására is. Ekkor az egyenlet
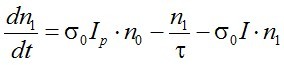 |
(2.16) |
alakú, ahol most Ip jelöli a gerjesztő intenzitást, I pedig az erősítendő jelét. Keressük meg a dn1/dt = 0 feltétel jellemzett stacionárius megoldást! Felhasználva n0 = n - n1 összefüggést
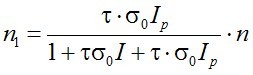 |
. | (2.17) |
Figyelembe véve, hogy az esetek egy jó részében az τσ0 Ip « 1, valamint az előbbiekben definiált It = 1/( τσ0) és az n10 = τσ0 Ip n jelölést bevezetve, n1-re
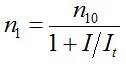 |
. | (2.18) |
adódik. Ebből világos n10 fizikai jelentése is, ha I = 0 akkor n1 = n10, vagyis a gerjesztett állapot populációja erősítendő jel (telítődés) nélkül. Az erősítési együtthatóra bevezetve a g = n1σ0 jelölést és (2.18) egyenlet mindkét oldalát σ0-val szorozva
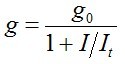 |
(2.19) |
kifejezést kapjuk a telítődő erősítésre, ahol g0 = n10 σ0. Amiből világosan látszik az erősítés telítődésében is az It játszik főszerepet: megadja azt az intenzitást, amely mellett g a g0 érték felére esik. Könnyen el tudjuk most már azt is képzelni, hogy milyen bonyodalmakat okoz egy időben változó jel alakhű erősítése, hiszen ha a jel első fele lecsökkenti az erősítést, a második rész kevéssé erősítődik, amely jelentős torzulást okozhat. A későbbiekben az erősítők tulajdonságairól még részletesen szólunk.
Amint az előző fejezetben már utaltunk rá, az atomi és molekuláris rendszerek abszorpciós és emissziós átmenetei sohasem monokromatikusak, hanem valamilyen véges sávszélességgel rendelkeznek. Kísérletileg vizsgálva egyre jobb feloldású spektrométereket használva, egy felbontás felett, a mért emissziós I(ν) függvény már nem változik. Egy ilyen függvény látható a 2.4. ábrán, ezt nevezzük a vonal profiljának és célszerű megjegyezni, hogy számos ilyen egy maximummal rendelkező függvény van, azonban későbbiekben látni fogjuk, hogy a spektroszkópiában lényegében csak két fajtája bír jelentőséggel.
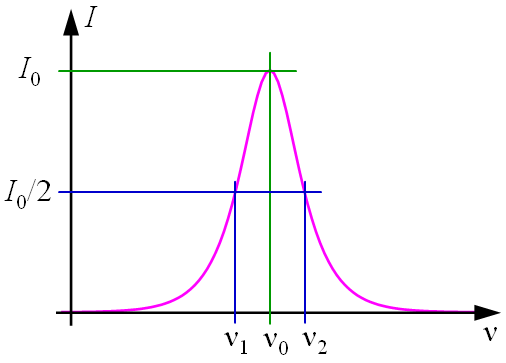
2.4. ábra. Emissziós spektrum intenzitásának frekvenciafüggése és a félértékszélesség (spektrális sávszélesség) értelmezése.
Gyakorlati és elméleti szempontból is célszerű a függvényt a szélességével jellemezni. A kérdés az, hogy mit nevezzünk annak. A széles körben elfogadott eljárás sávszélességnek (δν) nevezni annak a két frekvenciának (vagy hullámhossznak, körfrekvenciának) a különbségét melyeknél I(ν1) = I(ν2) = I(ν0)/2, a 2.4. ábra jelöléseit használva, δν = ν2 - ν1. Emiatt elterjedt a félértékszélesség elnevezés (angolul FWHM, amely a Full Width at Half Maximum kifejezés rövidítése). A sávszélesség eltérő lehet attól függően, hogy miben mérjük, de érdemes megjegyezni, hogy az ω = 2πν és a λ = c/ν összefüggéseket figyelembe véve, a relatív sávszélesség egyenlő mindhárom esetben, azaz
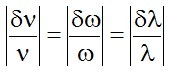 |
. | (2.20) |
A kísérletileg mért sávszélesség igen széles skálán mozog. Ugyanazon anyag esetén a kísérleti körülményektől függően, akár 1000-szeres különbség is lehet. A kiszélesedésnek számos oka van, az előző fejezetben említett legkisebb értékű a természetes vonalszélesség, amit a klasszikus modell a csillapodó rezgésekre vezet vissza, míg a kvantummechanika egyszerűen a Heisenberg-féle határozatlansági relációval magyarázza. A következő típusú az úgynevezett ütközési kiszélesedés, amely a sugárzó részecske oszcillációját ütközéssel megzavaró másik részecske hatására jön létre (új frekvencia komponensek jelennek meg). A harmadik az eddigieknél jelentősen nagyobb értékű kiszélesedés, az úgynevezett Doppler-féle kiszélesedés. Ennek fizikai eredete nagyon egyszerű: a sugárzó részecskék többnyire mozognak, miközben elnyelik vagy kibocsátják a fényt. Így a gyakorlatilag álló megfigyelő nem az eredeti frekvenciát figyeli meg, hanem a sebességtől (pontosabban a sebesség vektornak a megfigyelő felé eső komponensétől) függő Doppler-eltolódott frekvenciát. A minden részecskére egyforma természetes vonalszélességet és az ütközési kiszélesedést homogén kiszélesedésnek, a Doppler-félét pedig inhomogén kiszélesedésnek nevezzük, ahol minden részecske más és más eltolódással rendelkezik. Az eddigiek alapján még mindig nem tudjuk a függvények pontos alakját megadni, ezt majd meg a következő alfejezetben tesszük meg.
A fekete test sugárzásának a leírásánál már felhasználtuk a módusok számának meghatározásánál a Maxwell-egyenletekből származtatható (1.1) hullámegyenletet. Ott az egyszerűség kedvéért feltételeztük, hogy vákuumban vizsgáljuk a sugárzás tulajdonságait. A mostani esetben a
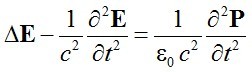 |
(2.21) |
inhomogén hullámegyenlet írja le a jelenséget, ahol P az anyag dipólmomentum-sűrűsége, ε0 a vákuum dielektromos állandója, továbbá c a vákuumbeli fénysebesség. Ahhoz, hogy az ilyen alakú hullámegyenlet megoldásait megvizsgáljuk, szükséges a P-nek ismerete.
Az anyag és sugárzás kölcsönhatásának első modelljét 1900-ban Lorentz dolgozta ki, az akkor még csak kezdetleges atomfizikai ismeretekre alapozva, de eredményesen leírva a törésmutató, az abszorpció és emisszió alapvető tulajdonságait. A 2.5. ábrán látható modell szerint a nehéz atommagot egy egyensúlyban levő elektronfelhő veszi körül külső erők nélkül.
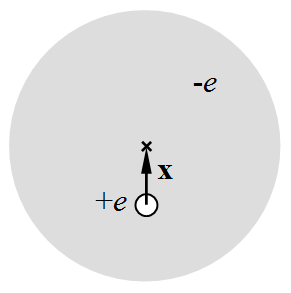
2.5. ábra. A klasszikus atom modellje.
Külső elektromos tér hatására ez az elektron felhő elmozdul, és egy rugalmas "visszatérítő" erő lép fel, amihez egy rugóállandó is rendelhető. A modell alapvető egyenlete:
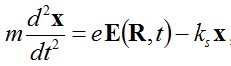 |
, | (2.22) |
ahol x az egyensúlyi helyzetből való kitérés, E a külső elektromos térerősség, e az elektron töltése, ks a rugóállandó és m az elektron tömege. Egyelőre, tekintsünk egy egy-elektronos modellt, ekkor az indukált dipólmomentum p = ex, ésamennyiben a részecskék koncentrációja N az indukált dipólmomentum sűrűség P = Np. Ezzel egy egy-elektront tartalmazó atom és az elektromos tér kölcsönhatását leíró modell birtokába jutottunk. Legyen a beeső fény egy ω frekvenciájú, z irányba terjedő síkhullám, vagyis az elektromos térerősséget az
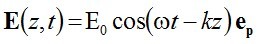 |
(2.23) |
képlet írja le, ahol k egy később meghatározandó állandó, és E0 nem függ t-től és z-től sem, ep pedig egy a z tengelyre merőleges egységvektor (polarizációs vektor). Ezt behelyettesítve az elektron mozgásegyenletébe
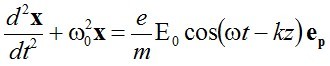 |
(2.24) |
egyenlet adódik. Ennek egy megoldása
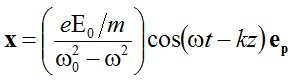 |
. | (2.25) |
Sokszor célszerű az indukált dipólmomentumot az
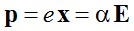 |
, | (2.26) |
alakban megadni, ahol α az úgynevezett polarizálhatóság. Esetünkben a (2.23), a (2.25) és a (2.26) egyenletek alapján
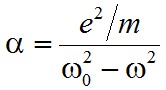 |
. |
Ezzel pedig a keresett dipólmomentum sűrűség
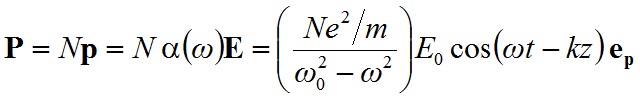 |
, | (2.27) |
és ez kerül a (2.21) inhomogén hullámegyenlet jobb oldalára. Az elmélet konzisztenciáját biztosítandó helyettesítsük P és E itt felvett alakját vissza! Az egyenlet érvényes, ha
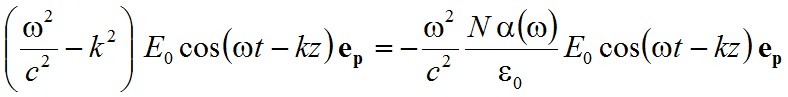 |
, | (2.28) |
amiből következik, hogy k-nak ki kell elégíteni a
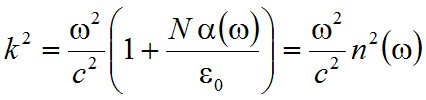 |
(2.29) |
diszperziós relációt, ahol n2(ω)
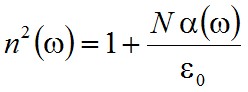 |
(2.30) |
alakú. Tehát a monokromatikus síkhullám megoldása a hullámegyenletnek vákuumban, ha
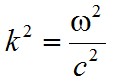 |
és anyagi közegben, ha
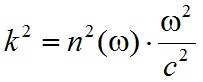 |
. | (2.31) |
Síkhullám esetén az anyagbeli fázissebesség
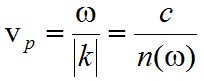 |
, | (2.32) |
amely tulajdonképpen az adott anyag törésmutatóját, n(ω)-t definiálja. Az itt bemutatott modell egyelektronos atomokra érvényes. Azonban a modell viszonylag könnyen általánosítható azzal a feltételezéssel, hogy minden elektron egymástól függetlenül válaszol a külső tér hatására, csak eltérő ki rugóállandóval. Ekkor a törésmutatóra Z számú elektron esetén az
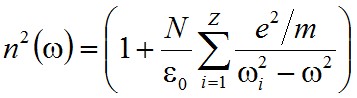 |
(2.33) |
alakú kifejezés adódik. Ezzel a modell a kísérleti adatokkal jól egyező módon írja le törésmutatónak a frekvenciától (vagy hullámhossztól) való függését.
A fentiekben bevezetett egyszerű modell továbbfejleszthető az abszorpció leírására is feltételezve, hogy az elektron rezgései során valamilyen, a sebességgel arányos "súrlódás" lép fel. Ebben az esetben már a matematikailag egyszerűbb komplex írásmódot használva - az elektron mozgásegyenlete
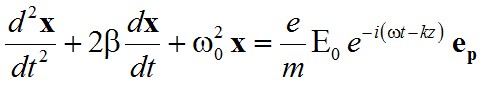 |
, | (2.34) |
ahol β = b/(2m) és ω0 = (k0/m)1/2. A komplex formalizmust a számolás egyszerűsége miatt alkalmazzuk, emlékezve arra, hogy a komplex fizikai mennyiségnek csak a valós vagy a képzetes részének tulajdonítható fizikai jelentés.
Keressük az x(t) megoldást az
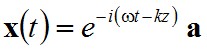 |
(2.35) |
alakban, ahol a k hullámszámot és az a vektort úgy választjuk meg, hogy x a (2.34) egyenlet megoldása legyen. Visszahelyettesítve (2.34) egyenletbe, a
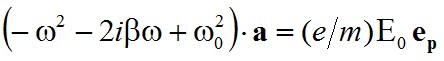 |
összefüggés adódik. Így az előbb feltételezett próbamegoldás kielégíti a mozgásegyenletet, ha
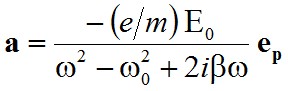 |
, | (2.36) |
amit felhasználva
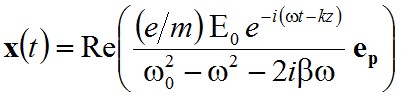 |
. | (2.37) |
Ez a megoldás nagyon hasonló a súrlódás nélküli csillapítatlan esetben kapott megoldáshoz. Határozzuk meg erre az esetre az indukált dipólusmomentumot! A p = ex alapján
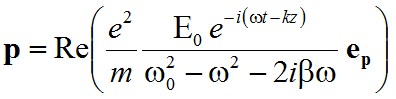 |
. | (2.38) |
Amelyből a fizikai jelentéssel bíró a valós rész
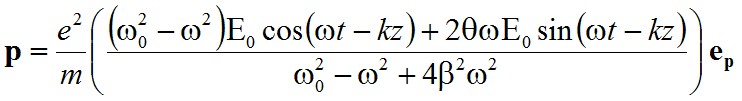 |
. | (2.39) |
A legfontosabb különbség a csillapítatlan esethez képest a számlálóban jelentkező szinuszos tag, ami azt jelenti, hogy az indukált dipólusmomentum nincs teljesen fázisban a külső térerősséggel. A komplex formalizmushoz visszatérve,
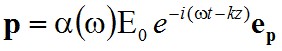 |
(2.40) |
alapján definiálható az α komplex polarizálhatóság. Mivel a két módon kifejezett p-nek egyenlőnek kell lennie ezért ez csak akkor lehetséges, ha
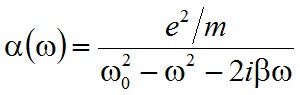 |
(2.41) |
alakú. Most már definiálható a komplex polarizálhatóság-sűrűség is:
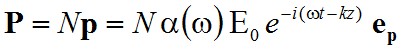 |
. |
A szokott módon visszahelyettesítve a (2.21) hullámegyenletbe a feltételezett komplex megoldást:
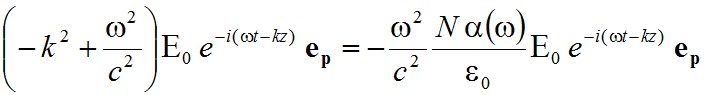 |
(2.42) |
adódik. Hasonlóan a korábbiakhoz a k-ra érvényes diszperziós reláció:
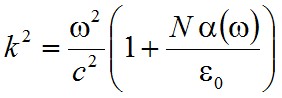 |
. | (2.43) |
Ebben az esetben miután α komplex, így az ε a közeg dielektromos állandójának és ezzel együtt az n törésmutatónak is komplexnek kell lennie,
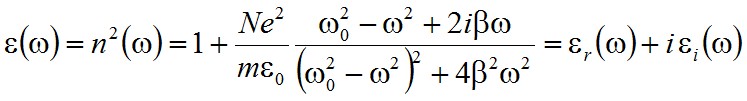 |
. | (2.44) |
A legfontosabb következménye ennek, hogy az elektromos tér másképpen viselkedik, mint eddig. A komplex törésmutatót valós és képzetes részével az függvényt n(ω) = nr(ω) + ini(ω) alakban felírva, az elektromos térerősséget
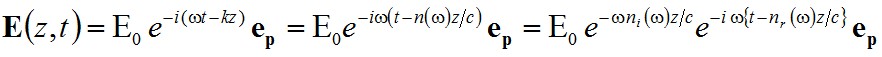 |
(2.45) |
formula adja meg. Amiből jól látszik, hogy E(z, t) többé nem tisztán oszcilláló, hanem ni(ω)-val meghatározott csökkenést mutat a z függvényében. Mivel az intenzitás arányos a térerősség valós részének négyzetével:
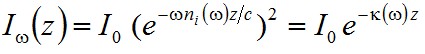 |
. | (2.46) |
Az intenzitás tehát exponenciális csökkenést mutat, ahol a csökkenés mértékét a
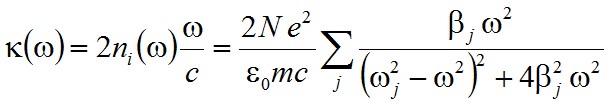 |
(2.47) |
az úgynevezett abszorpciós együttható határozza meg, ahol az explicit alak származtatásánál feltettük, hogy a (2.44) egyenletben az 1 után álló tag abszolút értéke sokkal kisebb, mint 1, így a gyökvonásnál közelítés használható. A fázissebességre vonatkozólag ugyancsak az E(z, t) függvényből láthatjuk, hogy c/nr(ω). Tehát, a komplex törésmutató valós része mutatja a fázissebességgel kapcsolatos törésmutató frekvenciafüggését (diszperzió), a képzetes komponens pedig az abszorpciót írja le. A törésmutató valós és képzetes részének a frekvenciafüggése a 2.6. ábrán látható. Az alacsony frekvenciás szakaszon nő a törésmutató valós része, ezt a szakaszt hívjuk normális diszperziónak (mivel a látható tartományban a legtöbb anyag így viselkedik), a rezonancia közelében gyors csökkenést mutat, ezt pedig anomális diszperziónak hívjuk. A törésmutató itt leírt viselkedése a kísérleti eredményekkel jó egyezést mutat.
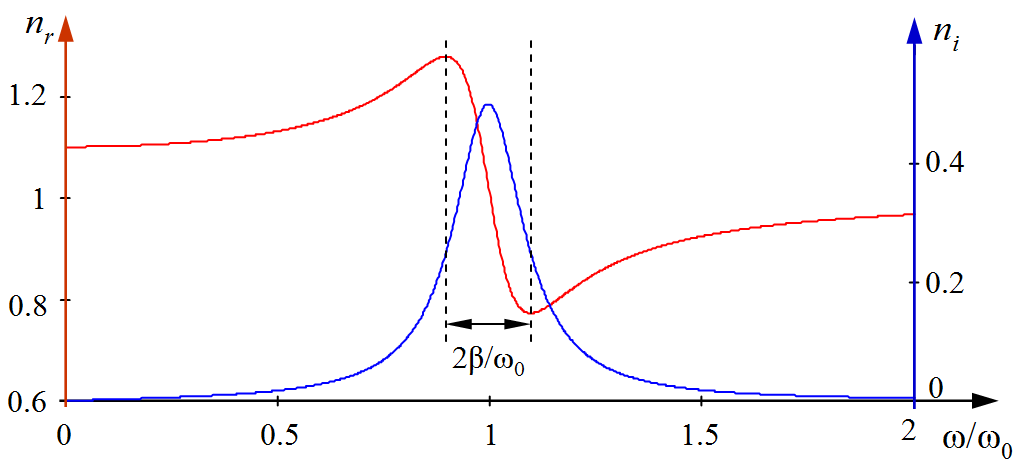
2.6. ábra. A Lorentz-féle modellből adódó komplex törésmutató valós (piros görbe) képzetes (kék görbe) részének frekvenciafüggése.
A komplex törésmutató képzetes részének frekvenciafüggése a fent megadott κ(ω) abszorpciós együtthatóból is megkapható ((2.47) egyenlet). Az előbb definiált abszorpciós együttható nyilvánvalóan a rezonancia közelében jelentős, tehát ahol ω0 - ω ≈ 0, ekkor a nevezőben lévő kifejezésben az ω02 - ω2 = (ω0 + ω)(ω0 - ω) = 2ω(ω0 - ω) közelítés megengedhető. Visszahelyettesítve, az egyszerűsítéseket elvégezve kapjuk az abszorpciós együttható új alakját:
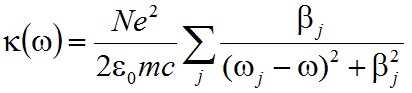 |
. | (2.48) |
Az összegzésben lévő függvényt f(x) = A/[(x - x0)2 + A2] Lorentz-féle függvénynek nevezzük. Könnyen látható, hogy a maximuma 1/A és ezt az x = x0 helyen veszi fel, továbbá félértékszélessége 2A. Az abszorpciós együttható változását a frekvenciával pedig Lorentz-féle profilnak, az itt kapott félértékszélességet pedig természetes vonalszélességnek szokás nevezni. Ez az érték csakis a részecskék paramétereitől függ, és mindegyik (azonos felépítésű) részecskére ugyanakkora. Például a látható tartományon az Na 589,1 nm-e vonalára 10 MHz nagyságrendű.
A Lorentz-modell alkalmas tehát az atomi folyamatokról szemléletes kép alkotására, nem számol viszont azzal a triviális problémával, hogy a kísérletek során pl. egy gázban végbemenő abszorpció mérésénél a kísérletezőhöz képest gyorsan mozgó részecskéket vizsgálunk. Mivel a forrás mozog, a Doppler-effektus miatt, a megfigyelő által észlelt frekvencia eltér a nyugalomban lévő forrás által sugárzásának frekvenciájától. A Doppler-féle eltolódást a forrás sebességnek a megfigyelő irányába eső sebességkomponense határozza meg. A megfigyelő irányába u z sebesség-komponenssel mozgó részecskék által kisugárzott ω0 körfrekvenciájú sugárzást a megfigyelő ω = ω0 ( 1 ± uz/c ) körfrekvenciának érzékeli, ahol c a közegbeli fénysebesség és közeledésre a +, míg távolodásra - jel vonatkozik. Hasonlóan abszorpció mérésénél is a mozgó részecskék elnyelési maximumát a Doppler eltolódással torzítva mérjük. Hőmérsékleti egyensúlyban a molekulák sebessége a Maxwell-féle eloszlást követi. Így T az abszolút hőmérsékleten, azon Ei energiájú részecskéknek koncentrációja, melyeknek a z irányú sebesség komponense uz és uz + duz közé esik
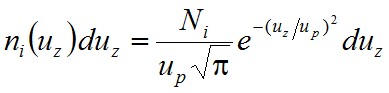 |
, | (2.49) |
ahol up = (2kT/m)1/2 az úgynevezett legvalószínűbb sebesség, m a részecskék tömege, k a Boltzmann állandó, Ni az Ei energiájú részecskéknek koncentrációja (vagyis ni(uz) függvény uz-szerinti integrálja). A Doppler-eltolódás egyenletéből uz = c(ω - ω0)/ω0, amiből differenciálással duz = (c/ω0) dω, ezzel pedig a (2.49) egyenlet alapján - az ω0-ról az ω és az ω + dω közé tolódott körfrekvenciájú részecskék koncentrációja
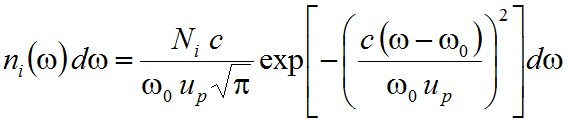 |
. | (2.50) |
Miután az elnyelt vagy kisugárzott fényteljesítmény arányos a részecskék koncentrációjával, a Doppler-féle effektus miatt kiszélesedett spektrumvonal intenzitását az
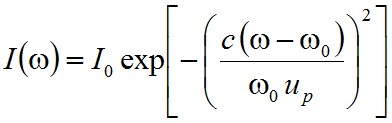 |
(2.51) |
formulával írhatjuk le. Ez pedig egy Gauss-féle eloszlást ír le a körfrekvencia függvényében, tehát a Doppler-kiszélesedés Gauss-féle intenzitásprofilt eredményez. A (2.51) egyenletből egyszerűen kiszámolható, hogy egy Doppler-kiszélesedett vonal sávszélességét a
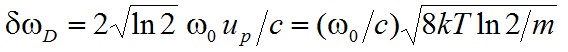 |
(2.52) |
formula adja meg. A δνD sávszélesség - a természetes vonalszélességnél már említett - Na D vonalára 500 K hőmérsékleten, 1.7·109 Hz nagyságú, ami a természetes vonalszélesség mintegy ezerszerese. Érdemes megjegyezni, hogy a Doppler kiszélesedés alapvetően eltér a természetes kiszélesedéstől, hiszen az egyedi részecskék nem mutatják, hanem csak az eltolódott frekvenciák a statisztikai átlaga mutatja.
Ismertesse az abszorpció telítődésének jelenségét!
Ismertesse az erősítés telítődésének jelenségét!
Mit értünk a spektrumvonalak félértékszélességén? Milyen kapcsolat van az spektrális szélesség és az időbeli hossz között?
Számítsa ki Lorentz-féle vonalalakból a természetes vonalalszélességet!
Milyen függyénnyel adható meg a Doppler-effektus következtében kiszélesedett spektrumvonal alakja?
Tartalom
Az előző fejezetben leírtuk, hogy az elektronikában az oszcillátorok létrehozásának szokásos módja, hogy egy erősítő kimenő jelének egy részét pozitív módon visszacsatoljuk a bemenetre. Az optikai tartományban ezt tükrökről való visszaverődéssel lehet a legegyszerűbben kísérletileg megvalósítani. Az olyan, általában tükrökből felépülő optikai rendszereket, amelyekben a fény oda-vissza haladva ugyanazon térrészen többször is áthaladhat, optikai rezonátoroknak nevezzük. Ilyen optikai rezonátorokat alkalmaznak többek között a lézerfizikában lézerfény generálására (lézer-rezonátorok) illetve abszorpciós spektroszkópiában kis koncentrációjú gázok kimutatására (Herriott cella).
Nyitott rezonátorok fogalma : Amint azt korábban láttuk, az egy foton által keltett kényszerített emisszió egyenlő az egy modusba jutó spontán emissziós fotonok számával. Ez a szám a látható tartományban szobahőmérsékleten 10-10 és 10-100 között van, míg a mikrohullámú tartományban ugyancsak szobahőmérsékleten 103 nagyságrendű. Ennek alapján érthető - sok más ok mellett - a fizikai alapja annak, hogy miért a maser-eket fejlesztették ki először. Egy lehetséges megoldás, ha a modusok számát (illetve sűrűségét) csökkenjük. A zárt üreg módusainak a számát jelentősen csökkenthetjük, ha megszüntetjük a zárt üreg falainak egy részét, és csak kettőt hagyunk meg. Ilyen módon az eddig zárt üreg helyett nyitott üreget hozunk létre. A két tükröt tartalmazó nyitott rezonátorra felírt hullámegyenletnek nem megoldása a síkhullám, mivel a tükrök véges átmérőjűek, és széleiken diffrakció lép fel. 1958-ban Schawlow és Townes amerikai, Prohorov szovjet kutatók megállapították, hogy a nyitott rezonátoroknak is vannak állóhullámú módusaik, és e módusok igen éles rezonanciát mutatnak (ez könnyen belátható, ha arra gondolunk, hogy egy aktív közeg nélküli nyitott rezonátor nem más, mint egy Fabry-Perot interferométer).
Ebben a fejezetben az ilyen optikai (nyitott) rezonátorok mátrixoptikai leírását adjuk meg különös tekintettel azok stabilitási tulajdonságaira.
A korábbiakban a fény terjedésének és anyaggal való kölcsönhatásának leírására annak hullám- és részecske (foton) természetét is kihasználtuk. Vizsgáltuk, hogyan terjed a fény és hogyan változik intenzitása és spektrális tulajdonsága erősítő és abszorbeáló közegekben. A fény terjedésének leírása optikai rendszerekben szintén megközelíthető ebből a két szempontból. A hullámoptikai leírásnál a nyaláb fázisfrontjának változását, míg a sugárterjedésen alapuló leírásnál végtelenül vékony nyalábok terjedését követjük végig az optikai rendszeren. Bár a két módszer a probléma megközelítésében lényegesen eltér egymástól, az eredmények kölcsönösen reprezentálhatóak. Sugárkövetéssel az optikai úthosszkülönbségek a rendszer apertúrájának bármely pontjában kiszámíthatóak és így a hullámfelület is meghatározható. A torzult hullámfelület ismeretében a rendszer optikai átviteli függvénye megadható.
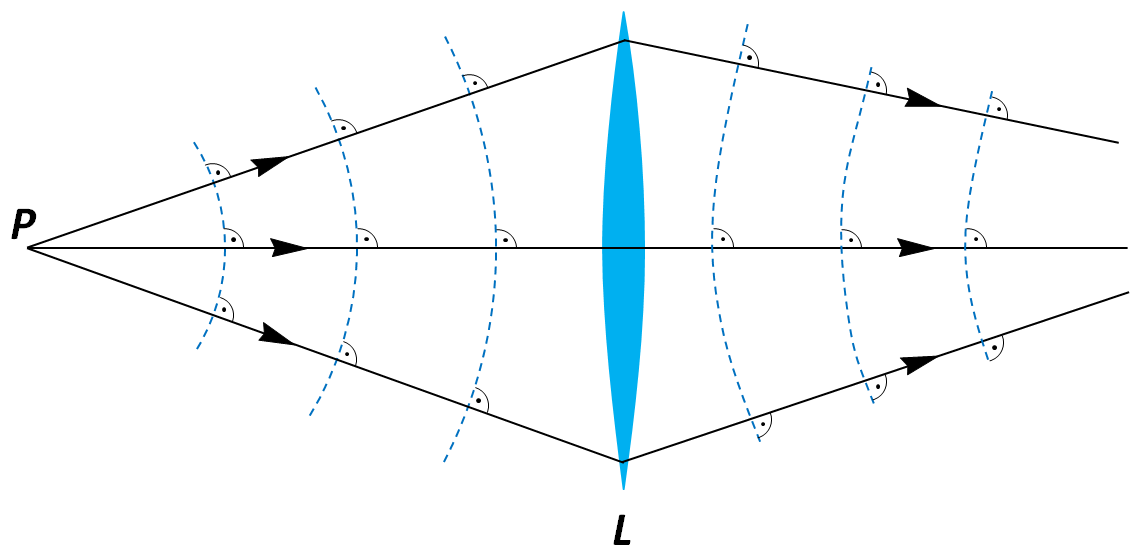
3.1. ábra. A pontszerű P fényforrás leírható a belőle radiálisan kiinduló fénysugarak (folytonos vonalak) és gömb fázisfrontok (szaggatott vonalak) segítségével. A sugarak mindig merőlegesek a fázisfrontra. Az L lencse eltéríti a sugarakat. A lencse után a fázisfrontok általában nem lesznek gömbfelületek (aberrációk lépnek fel), de mindig merőlegesek maradnak a fénysugarakra.
A hullámfront ismeretében a sugarak megszerkeszthetőek, feltételezve, hogy izotróp közegekben a sugarak iránya (azonos az energiaterjedést megadó Pointing vektor irányával) merőleges a fázisfrontra. A sugárkövetéses módszereknél végtelenül vékony diffrakciómentes sugarakat tételezünk fel, amelyek az egyes optikai felületeken vagy megtörnek, vagy visszaverődnek. Általában a sugarak nem hordoznak információt a fény intenzitásáról illetve polarizációs tulajdonságairól. Az intenzitásra az adott felületen áthaladó sugarak sűrűségéből következtethetünk. Egy sugarat az optikai tengelytől (z tengely) mert R távolságával és az azzal bezárt Θ szöggel jellemezhetünk. Meridionális sugarakat feltételezve az R távolság helyett gyakran használhatjuk az X vagy Y koordinátákat.
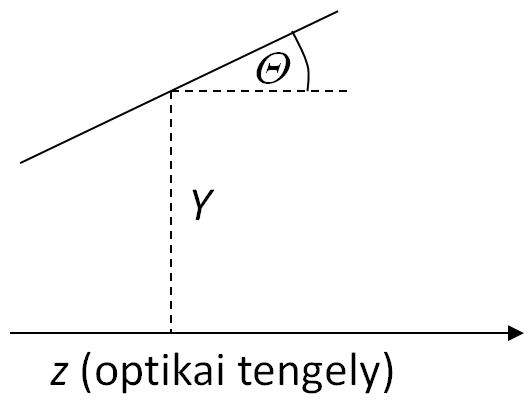
3.2. ábra. Egy sugarat egyértelműen megadhatunk az optikai tengelytől mért távolsággal (Y) és az azzal bezárt szöggel (Θ).
Konvenciók:
A sugarak balról jobbra terjednek.
A felületek távolsága a felületek optikai tengellyel való metszéspontjainak távolságával adható meg. A távolságot balról jobbra mérjük (pozitív irány).
A sugarak optikai tengelytől mert R távolsága pozitív, ha az optikai tengelytől felfelé mérjük.
A szögek pozitívak, ha az óramutató járásával ellentétes irányban mérjük őket.
A felületeket balról jobbra számozzuk.
A felület görbületi sugara pozitív, ha a görbületi középpont a felülettől jobbra helyezkedik el.
Általában igaz, hogy a sugarak az optikai tengellyel és az optikai felületekkel kis szöget zárnak be, ezért paraxiális közelítés alkalmazható.
Paraxiális közelítés: Kis szögek ( < 5º) esetén a trigonometrikus függvények pontos értékét jó közelítéssel ( < 1%) helyettesíthetjük azok Taylor sorának első tagjával (sin Θ ≈ Θ, cos Θ ≈ 1). A paraxiális közelítés jelentősen leegyszerűsíti az összefüggéseket, mert lineáris egyenletekké redukálja a korábbi trigonometrikus egyenleteket. Ezen lineáris egyenletek - ahogy később látni fogjuk - mátrixformalizmussal könnyen kezelhetőek.
Tekintsük először egy sugár terjedését szabad térben. Jelölje Y1 es Θ1 a sugarat megadó paramétereket a belépő síkban.
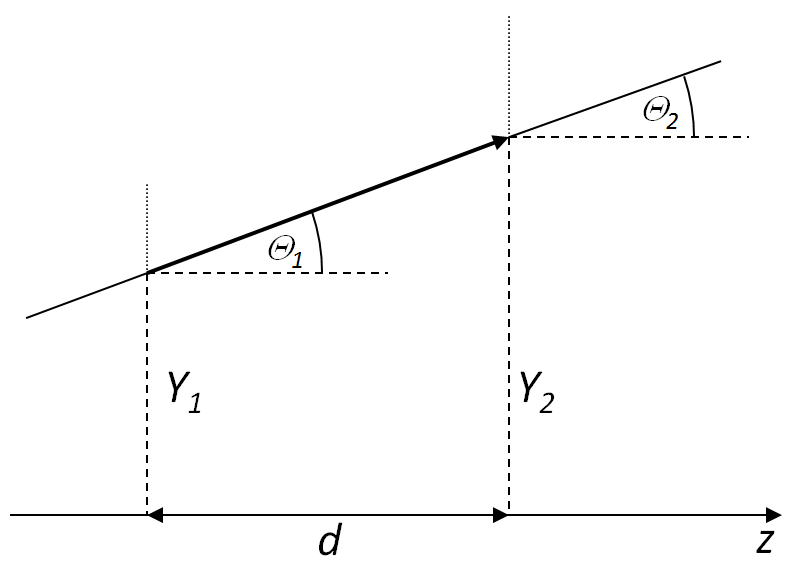
3.3. ábra. Terjedés szabad térben.
A tengely mentén d távolság megtétele után vákuumban vagy levegőben Y2 és Θ2-re írhatjuk:
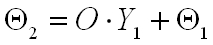 |
, | (3.1) |
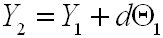 |
. | (3.2) |
E két egyenlet kifejezhető két mátrix szorzataként is:
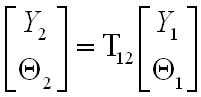 |
, | (3.3) |
ahol
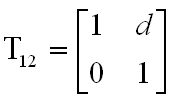 |
. |
T12 a szabad térben való terjedés átviteli mátrixa. A 3.3. ábrára merőleges X irányban hasonlóan írhatjuk:
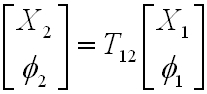 |
. | (3.4) |
Mindennek az eredménye az, hogy a szabad térben való terjedés triviális eredményeit kissé bonyolultan lehet megkapni, de később látni fogjuk, hogy bonyolultabb problémák megoldásánál jó hasznát vesszük a mátrixos kezelésnek.
Általánosságban a nyalábok terjedése leírható egy bemenő adatokat tartalmazó oszlopmátrix és egy úgynevezett ABCD átviteli mátrix szorzatával az alábbiak szerint:
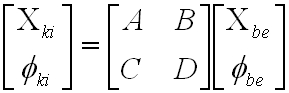 |
. | (3.5) |
Néhány gyakran használt optikai elem átviteli mátrixa
| szabad térben való terjedés: |
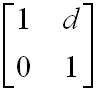 |
, | (3.6) |
| törés sík felületen: |
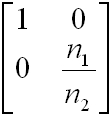 |
, | (3.7) |
| vékony lencsén való áthaladás: |
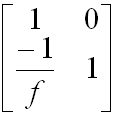 |
, | (3.8) |
| visszaverődés sík tükörről: |
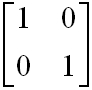 |
, | (3.9) |
| visszaverődés gömbtükörről: |
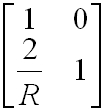 |
. | (3.10) |
Figyeljük meg, hogy az R sugarú gömbtükör és az f fókusztávolságú lencse átviteli mátrixa lényegében azonos, ha figyelembe vesszük a tükör fókusztávolsága és görbületi sugara között fennálló f = R/2 összefüggést. Továbbá az ABCD mátrix determinánsa megegyezik az optikai rendszert határoló közegek törésmutatóinak hányadosával (det(ABCD) = 1 ha a be- és kilépő oldalon a közeg azonos, pl. levegő). Az optikai elemeken való egymás utáni áthaladás és a köztük való terjedés együttesen a megfelelő mátrixok szorzata az alábbiak szerint: legyen az áthaladás szerint az átviteli mátrixok sorrendje M1, M2, M3, ... Mn, a végeredmény M = Mn ... M3 M2 M1. Figyeljük meg a fordított sorrendet!
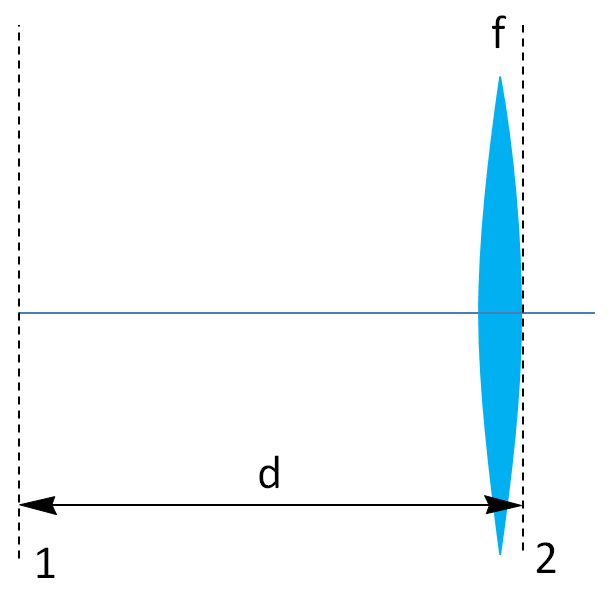
3.4. ábra. Terjedés egy d hosszúságú szabad térben és törés egy f fókusztávolságú lencsén.
Az eddigieknek megfelelően egy, az 3.4. ábrán látható elrendezésben az 1 síktól d távolságra lévő f fókuszú lencse után a 2-es síkban az átviteli mátrix:
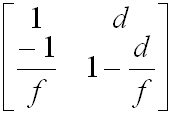 |
. | (3.11) |
Most számítsuk ki a fentiekben ismertetett, két párhuzamos síktükör által határolt nyitott rezonátor egy teljes körbejárásához tartozó K mátrixot. Egy teljes körbejárás két visszaverődést (R) és két szabad terjedést (T) megadó mátrixok szorzatával számítható ki: T12 R T21 R. Behelyettesítés után kapjuk:
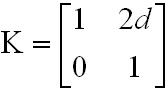 |
. | (3.12) |
Amennyiben k számú körre számolunk a teljes átviteli mátrix:
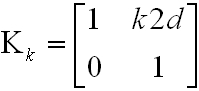 |
. | (3.13) |
Vegyük észre, hogy ez az előzőekben tárgyalt legegyszerűbb síktükrös rezonátor mátrixos tárgyalását jelenti. A Θi, Xi bemenő paraméterekkel a k kör utáni Xk és Θ k nyalábparaméterek az alábbi módon számíthatóak ki:
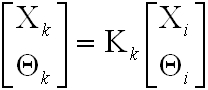 |
. | (3.14) |
Ezzel kiszámítható az a sugarú, d távolságú síktükrök között k kör megtétele milyen Θmax szöget enged meg, vagyis Xi= 0, Xk= a, ekkor a = 0+2kdΘmax , amiből
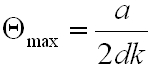 |
. | (3.15) |
adódik. A síktükrű rezonátorok a legegyszerűbb rezonátorok, de nagyszámú körbejárás csak az optikai tengellyel közel párhuzamos sugarak esetén érhető el. A tükrök csekély elállítása esetén a sugár hamar kilép a rezonátorból.
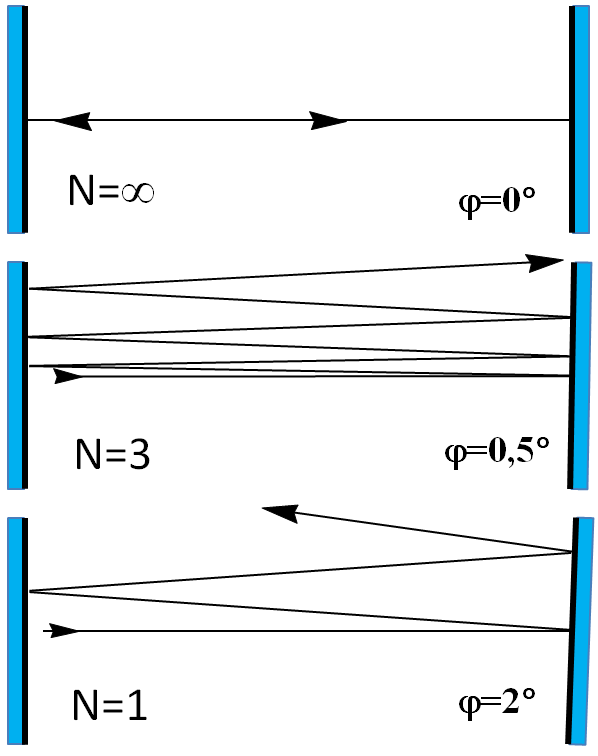
3.5. ábra. Sugárkövetés síktükrös rezonátorban, az egyik tükör kidöntése esetén. A teljes körbejárások száma (N) adott geometria mellett már 1º-os kidöntés esetén is jelentősen lecsökken.
Az eddig vizsgált rezonátorok két párhuzamos síktükörből álltak, és ebben az esetben stabil működést csak az Xi ≤ a és Θ = 0 esetén lehet kapni. Vagyis a rezonátor nagyon érzékeny több paraméterre is. A továbbiakban vizsgáljuk meg egy gömbtükör és egy síktükör alkalmazásával lehet-e ezen javítani. Legyen a gömbtükör görbületi sugara r, a két tükör távolsága d. Ekkor egy teljes körbejárás után az átviteli mátrix:
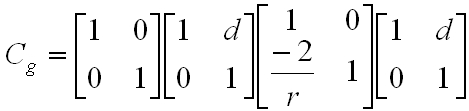 |
. | (3.16) |
A kijelölt szorzásokat elvégezve adódik a C g végső átviteli mátrix:
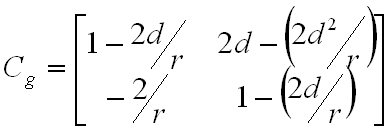 |
. | (3.17) |
Számoljuk ki X i , Θ i bemenő nyalábparaméterek mellett egy teljes körbejárás után a kimeneti paramétereket:
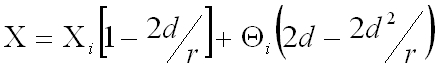 |
. | (3.18) |
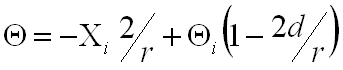 |
. | (3.19) |
Az egyenletekből látható, hogy a d = r feltétel teljesülése esetén az X független Θ i -től, ami jelentős javulás. Az ilyen rezonátorokat hemiszférikus rezonátoroknak nevezzük. Ebben az esetben az átviteli mátrix alakja egy teljes körbejárásra:
 |
. | (3.20) |
ugyanez n körbejárás esetén:
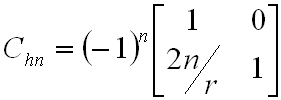 |
. | (3.21) |
Ezzel számítsuk ki, hogy X i , és Θ i hogyan változik n kör megtétele után:
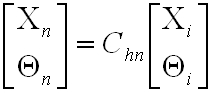 |
. | (3.22) |
Ezzel pedig X n , és Θ n egyenlete:
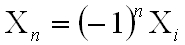 |
. | (3.23) |
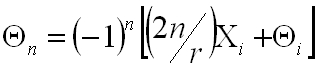 |
. | (3.24) |
Ebből látszik, hogy általános esetben nem stabil ez az elrendezés, ha azonban az Xi = 0 kezdeti feltételt választjuk, akkor Xn = 0, és Θn = (-1)n Θi adódik, ami azt jelenti, hogy a nyaláb önmagát ismételgeti. Természetesen továbbra is érvényes, ha Xi ≠ 0 akkor Θn ≠ Θi, vagyis a rezonátor nem stabil.
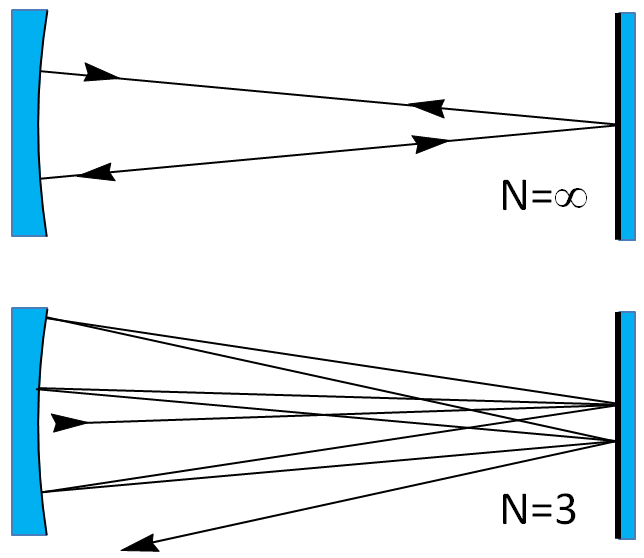
3.6. ábra. Sugárkövetés hemiszférikus rezonátorban. Optimális kivilágítás esetén a sugár végtelen sokszor önmagába verődik vissza. A kivilágítás szögét megváltoztatva a rezonátor stabilitása csökken.
Miután egy szférikus tükör alkalmazása lényegesen javította a stabilitást, vizsgáljuk meg a két szférikus tükröt tartalmazó rezonátor tulajdonságait. Legyen a két tükör görbületi sugara egyenlő (r), távolságuk pedig d. Ekkor az egy teljes körbejáráshoz tartozó mátrixok szorzata:
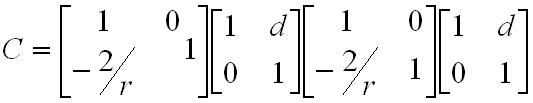 |
. | (3.25) |

3.7. ábra. Sugárkövetés konfokális rezonátorban. Optimális kivilágítás esetén a sugár végtelen sokszor önmagába verődik vissza. A gömbtükrökön fellépő aberráció miatt a körbejárás "nyomvonala" enyhén változik. A fekete vonal az első, a vörös vonal a 32-dik körbejárás nyomvonalát mutatja.
Elvégezve a kijelölt műveleteket a végeredmény egy meglehetősen bonyolult mátrix:
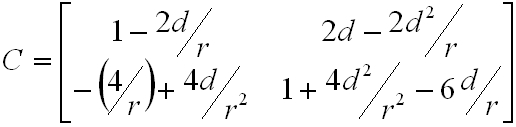 |
. | (3.26) |
Szerencsére drámai változásokat lehet előidézni, ha a d = r esetet választjuk, mert ekkor:
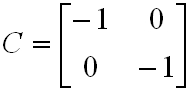 |
. | (3.27) |
Ami azt is jelenti, hogy X független a Θi-től, és n körre számítva:
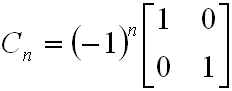 |
. | (3.28) |
Azaz n körre és (n+1) körre számítva X-nek és Θ-nak az abszolút értéke nem, csak az előjele változik periodikusan. Az ilyen rezonátort, amelyben a tükrök távolsága egyenlő a fókusztávolságuk összegével, konfokális rezonátornak nevezzük. Mint látható a nagyon stabilis rezonátor meglehetősen érzéketlen a nyaláb kezdő szögétől (paraxiális közelítést alkalmazunk!) ezért ezeket kis erősítésű és folytonos üzemű lézerekben alkalmazzák.
A stabilitás általános feltételét egy tetszőleges R 1 , R 2 görbületű sugarú és egymástól d távolságra lévő tükrökből álló rezonátorra is felírhatjuk. A korábbiakhoz hasonlóan számítsuk ki az egy teljes körbejáráshoz tartozó ABCD átviteli mátrixot és alkalmazzuk Sylvester törvényét:
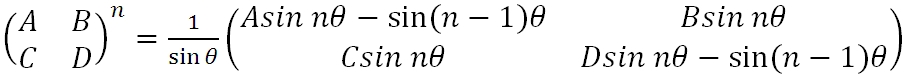 |
, | (3.29) |
ahol
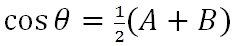 |
. | (3.30) |
Megmutatható, hogy a rezonátor akkor stabil, ha a teljesül a
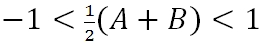 |
. | (3.31) |
feltétel, azaz a rezonátor paramétereire kifejezve:
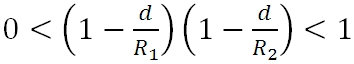 |
. | (3.32) |
Nem-stabil rezonátorok is léteznek, amelyek nem teljesítik az előző stabilitási feltételeket. Többek között nagy erősítésű lézerekben, amikor csak kevés körüljárásra van idő a minél nagyobb keresztmetszetű aktív közeg kihasználására alkalmazzák őket.
Milyen paramétereivel adható meg egyértelműen egy optikai
Adja meg az n2 törésmutatójú d vastagságú plánparalel lemez átviteli mátrixát, ha a külsőközeg törésmutatója n1!
Írja fel annak az optikai rendszernek a mátrixát, amelyet úgy kapunk, hogy megfordítunk egy ABCD mátrixszal jellemzett rendszert (a kimenő sík lesz a bemenő ill. fordítva)!
Egy optikai rezonátor tükreinek görbületi sugarai: R1 = 1 m és R2 = 1 m. A két tükör távolsága 50 cm. Stabil-e a rezonátor?
Tartalom
Az előző fejezetben láthattuk, hogy pusztán geometriai optikai megfontolásokból kiindulva lehetséges a rezonátorok stabilitásának a vizsgálata. Az ebből levont következtetések helytállóságát a gyakorlat igazolta, kísérletileg is sikerült lézereket, kollimált fénynyalábokat is léztehozni. Annak ellenére, hogy a közel párhuzamos lézernyaláb sokban hasonlít egy síkhullámhoz, intenzitásprofilja, terjedése nem írható le megfelelő módon a hullámegyenlet szokásos sík- és gömbhullám alakú megoldásaival. A lézernyalábok hullámoptikai leírásához a hullámegyenlet egy olyan megoldását kell megkeresni, mely egyezik a gyakorlati tapasztalatokkal.
A hullámegyenlet vákuumban érvényes alakja:
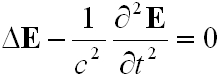 |
. | (4.1) |
A megoldást keressük a szokásos
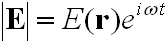 |
. | (4.2) |
alakban, vagyis egy időfüggő és egy helyfüggő tényezők szorzataként, amit visszahelyettesítve megkapjuk a hullámegyenlet helyfüggő (Helmholtz) alakját:
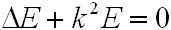 |
. | (4.3) |
A z irányban terjedő hullám megoldását keressük a következő alakban:
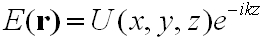 |
, | (4.4) |
ahol az exponenciális tag egy paraxiális síkhullám z irányú terjedését írja le, melyet egy lassan változó U(x, y, z) függvény (λ távolságon belül közel állandó) modulál. Írjuk vissza a Helmholtz egyenletbe a feltételezett megoldás függvényt:
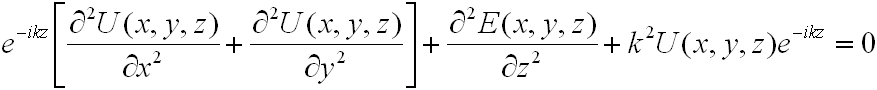 |
, | (4.5) |
ahol az E függvény z szerinti másodrendű parciális második deriváltja
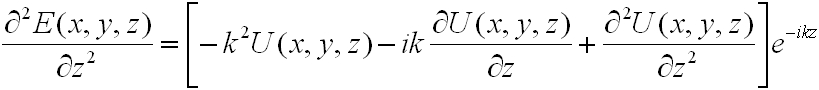 |
. | (4.6) |
Mivel U lassan változó függvény:
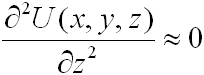 |
. | (4.7) |
A lehetséges egyszerűsítéseket elvégezve a (4.5) egyenletből a következő paraxiális hullámegyenletet kapjuk:
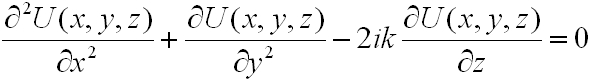 |
. | (4.8) |
Ennek egy lehetséges megoldása a parabolikus hullám:
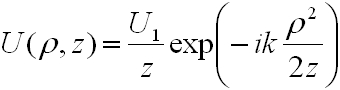 |
, | (4.9) |
ahol U1 egy konstans, ρ2 = x2 + y2 pedig a z tengelytől mért távolság négyzete. (Megj. A parabolikus hullám a gömbhullám paraxiális közelítése, amikor ρ « z.)
Egyszerű eltolással, q(z) = z - b, egy olyan parabolikus hullámot kapunk, melynek középpontja a b-ben van:
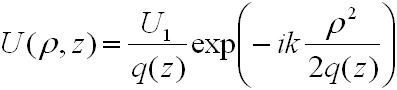 |
. | (4.10) |
Ha b komplex mennyiség, akkor is megoldása lesz a (4.8) paraxiális hullámegyenletnek. Legyen b = -iz0, vagyis q(z) = z + iz0, melyet komplex nyalábparaméternek nevezzük. Az amplitúdó és fázis szétválasztása céljából az 1/q(z)=1/(z + iz0) komplex számot valós és képzetes részre bontva
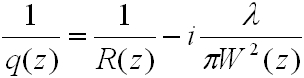 |
, | (4.11) |
és visszahelyettesítve a (4.10) egyenletbe a paraxiális hullámegyenlet komplex amplitúdójú megoldása (bizonyos helyettesítések bevezetésével) a következő lesz:
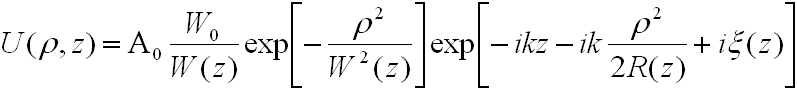 |
. | (4.12) |
A fenti egyenlet egy Gauss nyalábnak nevezet hullámot ír le, ahol
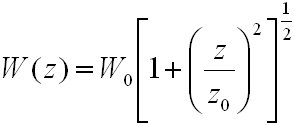 |
, | (4.13) |
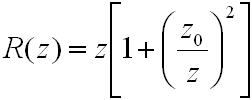 |
, | (4.14) |
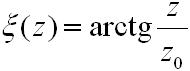 |
, | (4.15) |
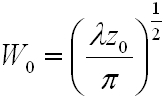 |
, | (4.16) |
az úgynevezett nyalábparaméterek, míg az A0=A1/iz0.
A meglehetősen bonyolultnak látszó megoldás igen szemléletes fizikai képet takar, melyet a következőkben mutatunk be. Az intenzitást, amit mérni tudunk, az amplitúdó négyzetéből számolhatjuk ki:
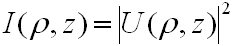 |
, | (4.17) |
ahonnan kapjuk, hogy
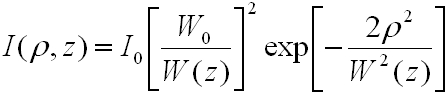 |
. | (4.18) |
Az így kapott függvény a z és a z tengelytől mért ρ távolság függvényében írja le az intenzitás változását mely a z tengelyre hengerszimmetrikus eloszlású. Az exponenciális tag a z-től mért távolság szerint egy Gauss (exp(-ρ2) alakú) függvény (lásd 4.1.ábra), melynek maximuma a ρ = 0-nál van, innen ered a Gauss nyaláb elnevezés.
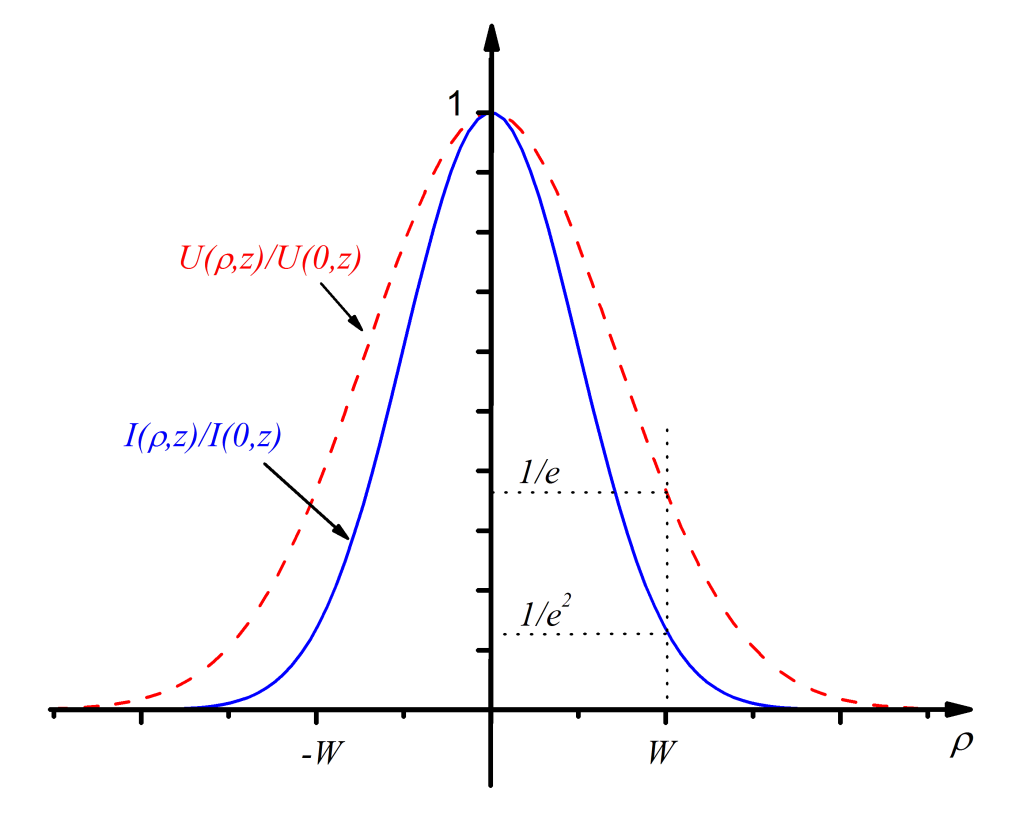
4.1. ábra. A Gauss nyaláb térerősségének és intenzitásának normált eloszlása a z tengelytől mért távolság függvényében.
W(z) fizikai jelentését könnyen megkapjuk, ha a ρ = W(z) behelyettesítést elvégezzük (4.12)-ben. Ekkor az első exponenciális tag 1/e lesz, ami azt jelenti, hogy W(z) az a z tengelytől mért távolság, ahol a térerősség az e-ad részére esik, ezért ezt a nyaláb sugarának nevezzük. Természetesen a 2W(z) a nyaláb átmérője. Ez alapján a W(z) függvény írja le a z irányú terjedés során a nyalábsugár változását, z = 0 helyettesítéssel W0 = W(0), ami a függvény minimuma. W0 fizikai jelentése, hogy ez a minimális nyalábsugár amit nyalábnyaknak is szokás nevezni (4.2 ábra).
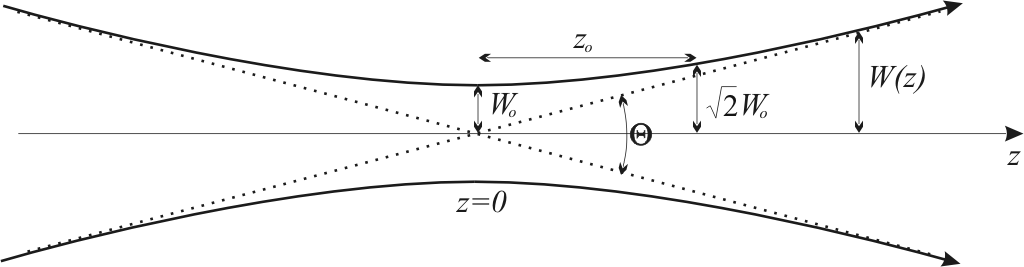
4.2. ábra. A Gauss nyaláb sugarának változása a terjedés során.
További információt kaphatunk a z = z0 helyettesítéssel, ekkor W = W0√2, vagyis z0 az a távolság, amelyen belül a nyaláb sugár a √2 szeresére nő. A z0 mennyiséget Rayleigh hossznak nevezzük, ha |z| < z0 akkor közeli zónáról beszélünk, ha |z| » z0 akkor távoli zónáról. Megjegyezzük, hogy az itt használt ábrák elsősorban a szemléltetést szolgálják, a valóságban egy 632,8 nm hullámhosszú W0 = 1 mm-es nyaláb esetén a z0-nak 5 m körüli értéke van. Amint az ábráról is jól látszik a távoli zónában a nyaláb széttartása már egyenletes, vagyis ha |z| « z0 akkor (4.13)-ban 1 « |z/z0|. Ezzel az egyenlet W(z) = W0 |z/z0|-ra egyszerűsödik, ami egy egyenes egyenlete. Az egyenesnek a z tengelyhez viszonyított iránytangense
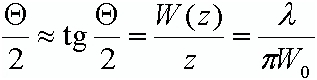 |
, | (4.19) |
melynek kétszeresét (Θ) a nyaláb divergenciájának (széttartásának) nevezünk. A széttartás mértéke jellemzően nagyon kicsi, az előző példa adataival számolva Θ = 0,4 mrad ≈ 0,23°. Érdemes megjegyezni, hogy a (4.13) egyenletet átrendezve (W/W0)2 - (z/z0)2 = 1 egyenlethez jutunk, amely egy hiperbola egyenlete, melynek a W(z) = W0 |z/ z 0| egyenesek az asszimptotái. Ennek megfelelően a nyalábfolt sugara egy hiperbola mentén változik és távol a nyalábderéktól, ahol a hiperbola egyre inkább megközelíti az asszimptotáit, a nyalábfolt sugara a z koordináta lineáris függvényével közelíthető.
Visszatekintve a 4.1. ábrára látható, hogy a Gauss függvény a középponttól távolodva szimmetrikusan csökken és a végtelenben 0-hoz tart. A gyakorlatban viszont véges átmérőjű optikai elemeken megy keresztül a nyaláb. Kérdés, hogy milyen átmérő mellett lehet elhanyagolni a kitakart szélek intenzitását. Ha az apertúra méretét 2W-nek választjuk, akkor 86%-os áteresztéssel számolhatunk, ami még kevés, de πW-nek választva már 99%-os transzmissziót lehet elérni. Hasonló gyakorlati probléma, hogy a Gauss nyalábot W √(2) átmérőjű konstans intenzitású nyalábbal (cilinder, vagy top hat profil) lehet helyettesíteni.
Az eddigiekben a megoldásnak az amplitúdó változását leíró részét vizsgáltuk, de a fázisviszonyokat leíró rész is fontos információkat tartalmaz. A (4.12) egyenlet szerint a Gauss nyaláb fázisa:
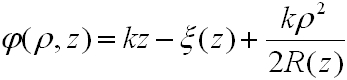 |
. | (4.20) |
A nyaláb tengelyében
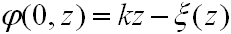 |
. | (4.21) |
ami eltér a síkhullámra jellemző kz értéktől. Ez a fáziskésés, melyet Gouy eltolódásnak nevezzük -∞-nél -π/2 és folyamatosan nő, +∞-nél +π/2. A (4.20) egyenlet jobb oldalának harmadik tagja írja le a parabola alakú fázisfront görbületét, ahol R(z) a hullámfront görbületi sugara a z tengelynél. Az R(z) előbb bemutatott (4.14) alakjának vizsgálatával szintén fontos információkhoz lehet jutni. Tegyük fel, hogy a minimális átmérőnél vagyunk (z = 0), ekkor az R(z) a végtelenhez tart, azaz síkhullámról beszélhetünk, sík fázisfrontunk van (4.3 ábra). Vizsgáljuk meg a másik végletet: amikor |z| » z0 a zárójelben lévő kifejezés második tagja 0-hoz tart, vagyis R(z) = z. Ebben az esetben a görbületi sugár a 0-tól mért távolsággal egyenlő, vagyis gömbhullám szerű. A hullámfront görbületi sugara z = ±z0-nál a legkisebb és ennek értéke ±2z0.
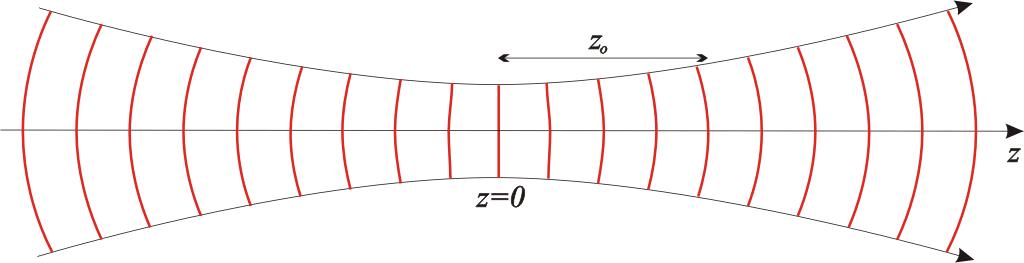
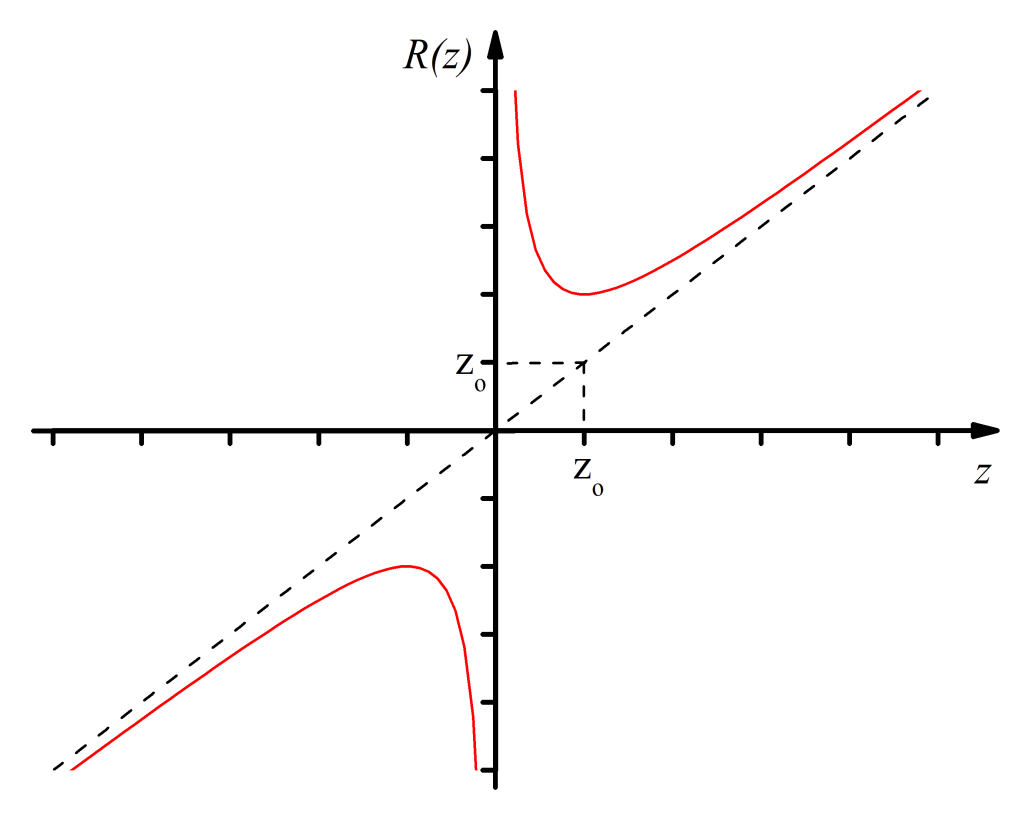
4.3. ábra. A hullámfront görbületének változása a Gauss nyaláb terjedése során, valamint a R(z) függvény grafikus ábrázolása.
A paraxiális hullámegyenlet itt bemutatott megoldása egyelőre csak matematikai eredmény, a kérdés az, hogy kísérletileg hogyan lehet olyan feltételeket teremteni, ami a Gauss nyaláb kialakulásának kedvez. Vegyünk egy λ, W0 paraméterekkel jellemzett Gauss nyalábot amint azt a 4.4. ábrán mutatjuk be.
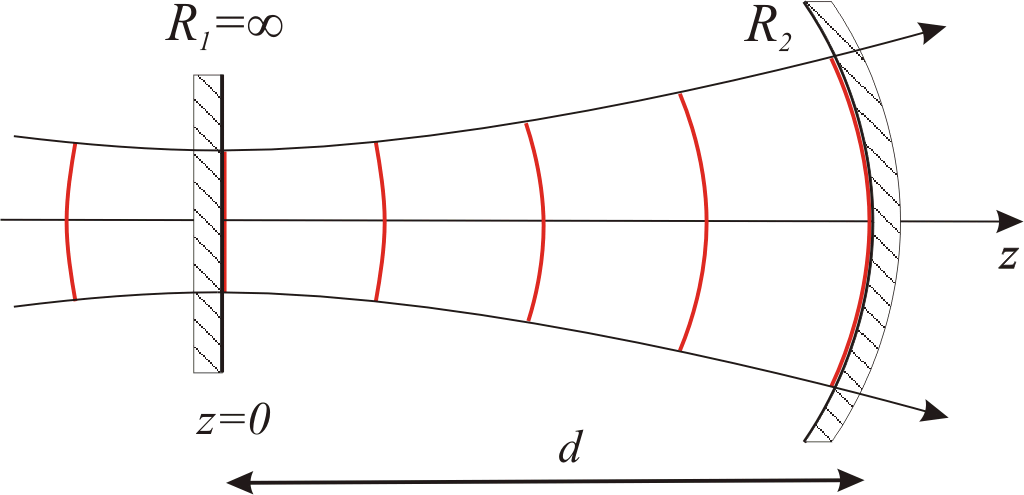
4.4. ábra. Rezonátor illesztése a kívánt paraméterekkel rendelkező Gauss nyalábhoz.
A z = 0 helyen helyezzünk el egy síktükröt (itt a fázisfront sík), ettől d távolságra egy olyan gömbtükröt, amely pontosan egybeesik az adott helyen a nyaláb fázisfrontjával (R2 = R(d)) és máris van egy rezonátorunk. A (4.14) egyenlet ezen feltételek mellett a következőképpen alakul:
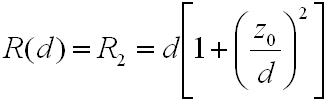 |
, | (4.22) |
Ebből kifejezhető a z0:
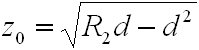 |
, | (4.23) |
aminek csak akkor van valós megoldása, ha 0 ≤ d/R2 ≤ 1. Az adott példában szereplő tükrök segítségével akkor tudunk stabil rezonátort létrehozni, ha a köztük levő távolság kisebb, mint homorú tükör görbületi sugara. Ez az eredmény megegyezik azzal, amit az előző fejezetben a mátrix-optikai tárgyalás adott egy hasonló elrendezés esetén. A Gauss nyaláb alakjának a d távolságtól való függését bemutató animáció itt nézhető meg. A rezonátorban létrejövő hullám λ értékét az aktív közeg anyaga, W0-t pedig az aktív közeg méretei határozzák meg. Ezzel minden információ birtokában vagyunk, minden szükséges paraméter kiszámítható. Az ilyen rezonátor által létrehozott nyalábnak a terjedési irányra merőleges (x, y) síkban létrejövő intenzitás eloszlását nevezzük transzverzális módusnak (Transverse ElectroMagnetic, TEM).
A Helmholtz egyenlet fennebb bemutatott megoldása a "legegyszerűbb", ezen kívül természetesen számos más függvény is megoldás lehet. Ezek közül kiemelendők azok, amelyek fázisfrontja gömbszerű, mivel ezekhez lehet könnyen a fenti módon rezonátort illeszteni. Ilyenek a négyzetes szimmetriájú Hermite-Gauss és a hengerszimmetriájú Laguerre-Gauss polinomok, amelyek közül a legegyszerűbb a 00 indexszel (TEM00) jelölt egyetlen maximummal rendelkező Gauss függvény. A lézerek többségében a Hermite-Gauss polinomokkal leírható magasabb rendű módusok tudnak kialakulni, melynek oka leggyakrabban a ferdeszögben elhelyezett Brewster ablak, de a rendszerben levő valamilyen kisméretű asztigmatizmus is az ilyen négyzetes szimmetriájú módusok kialakulásához vezet. A TEM mp módushoz tartozó térerő- és intenzitáseloszlást az (x, y, z) derékszögű koordinátarendszerben a következő összefüggések írják le:
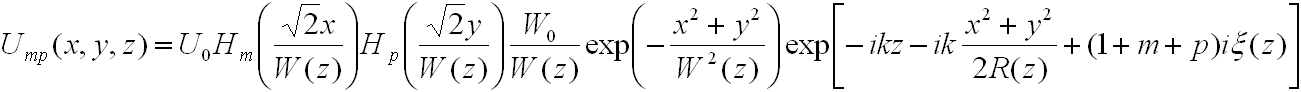 |
, | (4.24) |
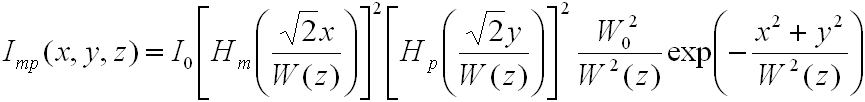 |
, | (4.25) |
ahol
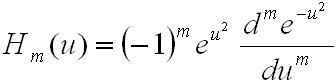 |
, | (4.26) |
az m-ed rendű Hermite polinom, W(z) a 00 alapmódushoz tartozó nyalábátmérő és U0, valamint I0 az alapmódushoz tartozó értékek a nyalábnyak középpontjában. A módusok indexe megadja az adott tengelyen (x vagy y) a térerősségeloszlásban megfigyelhető csomópontok számát. A csomópontok két oldalán a pillanatnyi térerősségvektorok ellentétes irányításúak (4.5. ábra).
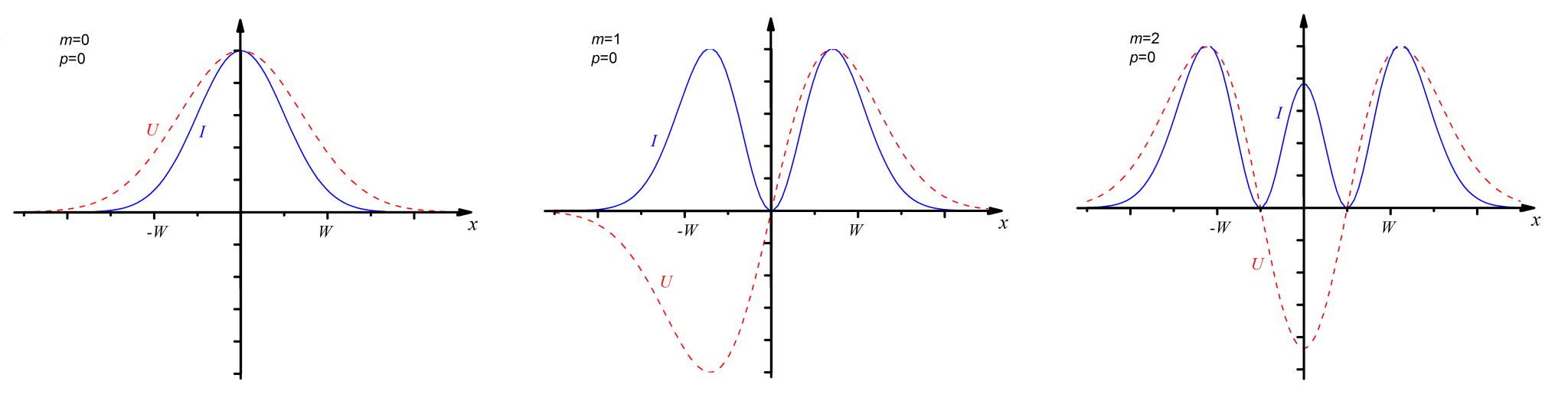
4.5. ábra. A normált térerősség- és intenzitáseloszlás az x tengely mentén a 00, 10 és 20 Hermite-Gauss módusok esetén.
Megjegyezzük, hogy a magasabb rendű módusok fázisfront görbülete és divergenciája megegyezik a 00 módussal, csak a nyaláb mérete növekszik az indexek emelkedésével. Ez jól látható a 4.6. ábrán is, amely néhány TEM mp módus intenzitáseloszlását mutatja az (x, y) síkban. Ezt a tulajdonságot kihasználhatjuk a magasabb rendű módusok elnyomására. Ha egy megfelelő méretű apertúrát helyezünk a rezonátorba, a magasabb rendű módusok energiavesztesége nagyobb lehet, mint az erősítés, ami gátolja ezek kialakulását. Például, míg egy πW átmérőjű apertúra a TEM00 módus 99%-át átengedi, addig már a TEM01 módusnál már ~6%-os veszteséget okoz.

4.6. ábra. Hermite-Gauss módusok intenzitáseloszlása a terjedési irányra merőleges síkban. (www.wikipedia.org)
Nagyon jó hengerszimmetriával rendelkező lézereknél kialakulhatnak a hengerszimmetrikus (Laguerre-Gauss) TEM pl módusok is, ahol p és l a radiális, illetve polár indexeket jelentik. Az eloszlást leíró egyenletek mellőzésével a 4.7 ábrán néhány jellemzőbb intenzitásprofil látható.

4.7. ábra. Hengerszimmetrikus Laguerre-Gauss módusok intenzitáseloszlása. (www.wikipedia.org)
Mivel a lézereknek gyakran a fókuszált fényét alkalmazzák, fontos a lefókuszáláskor keletkező foltméret meghatározása. A Gauss nyalábok általában jól jellemezhetőek a q(z) komplex nyaláb paraméterrel, azzal az előnnyel, hogy ha egy optikai elem átviteli mátrixa ABCD, akkor ezt a q transzformációjára lehet használni. Másképpen, ha egy Gauss nyaláb q1 bemeneti paraméterrel rendelkezik, a kimenő nyaláb egy q2 paraméterrel rendelkező Gauss nyaláb lesz, melyre fennáll a következő összefüggés:
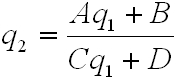 |
. | (4.27) |
A fenti összefüggésre nincs általános levezetés, de bármilyen optikai elem átviteli mátrixa esetére külön-külön bizonyítható az egyenlet érvényessége. A számítások egyszerűsítése érdekében tekintsük azt a 4.8. ábrán szemléltetett esetet, amikor egy Gauss nyalábot a nyalábnyaknál elhelyezett vékony lencse segítségével fókuszálunk.
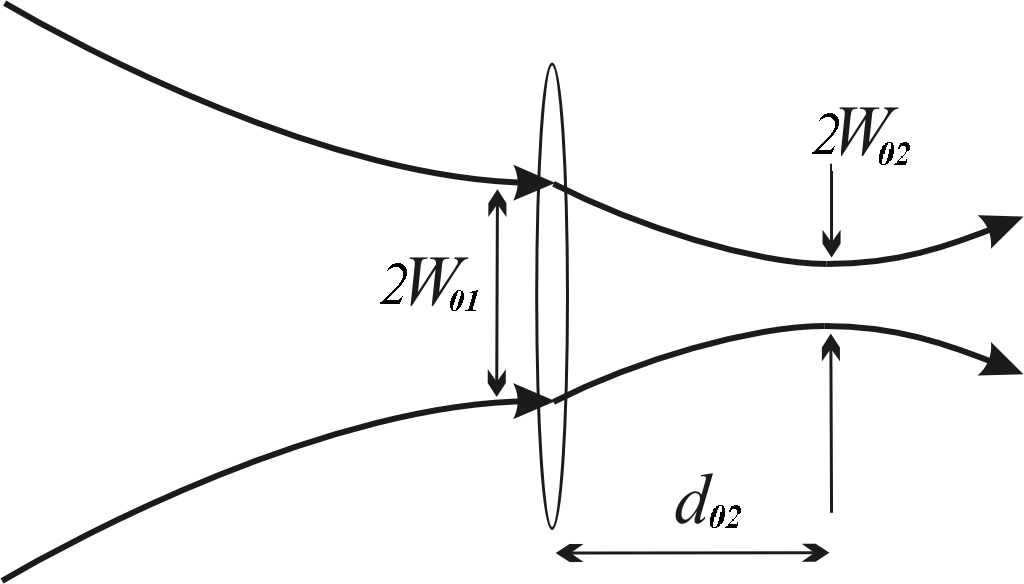
4.8. ábra. Gauss nyaláb transzformációja lencsével.
A kiindulási feltételeknek megfelelően a lencse baloldalán az R1= ∞ és q1=iπ(W01)2/λ. A kérdés az, hogy a lencse után mekkora d távolságra keletkezik egy nyalábnyak és mekkora lesz itt a nyaláb W02 sugara. Az ABCD mátrix elemeinek meghatározásához számítsuk ki az f fókusztávolságú vékony lencse és a szabad térben való terjedés mátrixának a szorzatát:
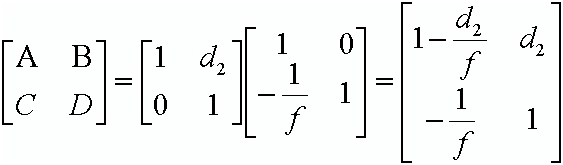 |
, | (4.28) |
A kimenő q2 paraméter reciproka a következő lesz:
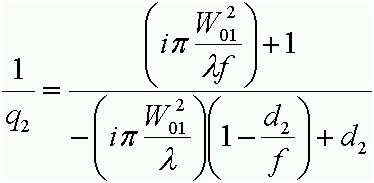 |
, | (4.29) |
melyben különválasztva a valós és képzetes részeket adódik, hogy:
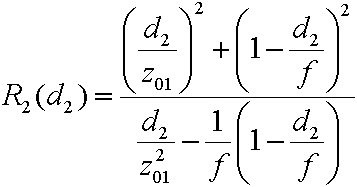 |
, | (4.30) |
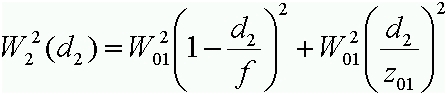 |
, | (4.31) |
A fenti két egyenlet egy tetszőleges d2 helyen írja le a görbületi sugarat és a nyaláb méretét. Figyelembe véve, hogy olyan helyet keresünk, ahol R2(d2) végtelenné válik a (4.30) egyenlet nevezője zéró kell legyen. Így azt kapjuk, hogy
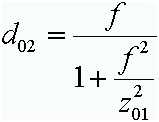 |
, | (4.32) |
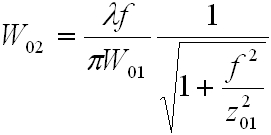 |
, | (4.33) |
Az eredmény két dolgot mutat, az egyik, hogy a nyaláb nyak igen kicsinnyé válhat; a másik, hogy nem f távolságra van a lencsétől ez a minimális foltátmérő. Ugyanakkor, ha visszagondolunk a z0-ra tett becsléseinkre (z0 = 5 m) a nevezőkben lévő korrekciós tagok elhanyagolhatóvá válnak, vagyis az esetek egy részében a d02 = f és W02=f∙Θ1 elfogadható közelítés. Jól látható, hogy a jellemzően alacsony divergencia miatt a Gauss nyalábok nagyon jól fókuszálhatók. Az itt megnézhető animáció a fókuszált Gauss nyaláb alakjának a d01 nyalábnyak-lencse távolságtól való függését mutatka be adott W01 esetén. Jól látható, hogy a minimális foltátmérő helyzete a d01 növelése során a lencsétől távolodva túllép a fókuszponton, majd pedig újra közeledni kezd hozzá. Egy másik jellemzője a Gauss nyaláboknak, hogy míg a kétszeres fókuszból kiinduló gömbhullámokat a lencse a túloldali kétszeres fókuszban gyűjti össze, a lencsén átmenő Gauss nagyáb alakját nagymértékben befolyásolja a nyaláb is a lencse viszonyát jelző N=(W01)2/(λf) Fresnel szám (animáció itt).
Milyen előnyei vannak a Gauss nyaláboknak a lézerek szempontjából?
Adott egy-egy R görbületi sugarú homorú és domború tükör. Vizsgálja meg, hogy lehetséges-e stabil rezonátort építeni a tükrök segítségével, és ha igen, milyen feltételek mellett.
Egy egyszerű konfokális rezonátor tükreinek fókusztávolsága 0,5 m és a tükrök közötti távolság d = 1 m. Tegyük fel, hogy a rezonátorban egy λ = 500 nm hullámhosszúságú TEM00 módusú Gauss nyaláb oszcillál. Mekkora a nyaláb z0 Rayleigh-hossza és a W0 nyalábnyak? Mennyi a nyaláb divergenciája? Mekkora a frekvenciakülönbség a TEM0,0,q és TEM0,0,q+1 longitudinális, valamint a TEMm,p,q és a TEMm+1,p,q transzverzális Hermite-Gauss módusok között MHz-ben kifejezve? Értelmezze az eredményt.
Az előző feladatban leírt rendszer esetén mekkora kell legyen a 99%-os reflexiójú 1-es tükör minimális átmérője, ahhoz, hogy visszaverődéskor a veszteség kisebb legyen, mint 2%?
Igazolja, hogy adott méretű apertúrán való áthaladáskor a TEM10 módusnak nagyobb a vesztesége, mint az alapmódusnak.
Egy 1 mm átmérőjű, 0,25 m Rayleigh hosszal rendelkező 632,8 nm-es Gauss nyalábot egy 1 cm-es fókusztávolságú vékonylencsével fókuszálunk. A lencsétől milyen távolságra és mekkora lesz a legkisebb foltméret?
Tartalom
A lézerek működéséhez az aktív anyagban populáció inverziót kell elérni, azaz a gerjesztett állapotban lévő részecskék száma meg kell hogy haladja a - lézerátmenet alsó energiaszintjét jelentő - alapállapot betöltöttségének a szintjét. A háromnívós lézertípusoknál (pl. rubinlézer) ez ténylegesen az alapállapot intenzív gerjesztését kívánja, míg a négynívós rendszerekben (Nd-YAG, stb.) a lézerátmenet alsó nívója gyakorlatilag üres.
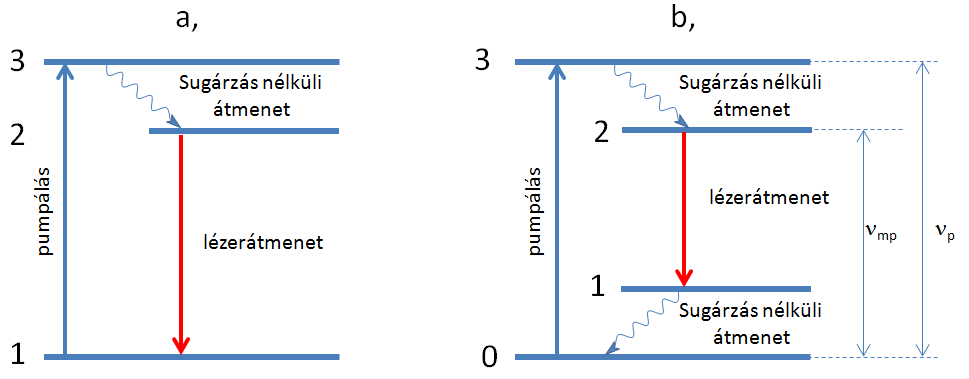
5.1. ábra. (a) Három- és (b) négy-energianívós rendszerek vázlata. A három-energianívós rendszerben az (1) alapállapotból a (3) gerjesztett állapotba pumpált részecskék egy gyors sugárzásmentes átmenettel kerülnek a lézerátmenet felső energiaszintjét jelentő (2) energianívóra. A négy-energianívós rendszerekben a lézerátmenet alsó energianívója nem egyezik meg az alapállapottal, ezért termikus egyensúlyban alacsony betöltöttségű.
Az aktív anyagban a lézerek működéséhez szükséges populáció inverziót optikai pumpálással (koherens, inkoherens), elektronütközéssel (rugalmas, rugalmatlan) vagy kémiai reakciókkal érhetjük el. A következőkben ezen gerjesztési módszereket ismertetjük.
Inkoherens optikai gerjesztés során az aktív anyagot nagyteljesítményű lámpával gerjesztik. Ezen pumpálási mechanizmus ideális szilárdtest és folyadék-lézerek gerjesztésére, mert a közegekben szélesek az abszorpciós vonalak (lsd. 2. fejezet), így jobb hatásfokkal nyelik el a nagy sávszélességű pumpáló nyaláb fényét. A gerjesztés hatásfokát definiálhatjuk, az adott gerjesztési ráta (Rp) eléréséhez szükséges minimális gerjesztési teljesítmény (Pm) és a rendszer által felvett elektromos teljesítmény (Pp) hányadosaként:
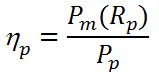 |
. | (5.1) |
Homogén gerjesztési rátát feltételezve a minimális gerjesztési teljesítmény
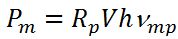 |
, | (5.2) |
ahol V az aktív közeg térfogata és hνmp a lézerátmenet felső energianívója és az alapállapot közötti energiakülönbség (lsd. 5.1. ábra). Inhomogén pumpálás esetén egy átlagos rátával kell számolni:
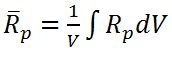 |
, | (5.3) |
ahol az integrálás a teljes térfogatra kiterjed.
A pumpálás eredő hatásfoka négy tényező függvénye:
η r (radiative efficiency): A lámpa emissziós hatásfoka, amely megmutatja, hogy mekkora fényteljesítményt képes a lámpa az aktív anyag gerjesztésére alkalmas hullámhossztartományba konvertálni. Xenon és kripton lámpákkal gerjesztett rubin- és neodímiumlézerek esetén az emissziós hatásfok tipikusan 30-40%. Mivel az emissziós spektrum függ a lámpára kapcsolt áram nagyságától, az emissziós hatásfok is áramsűrűség függő. Nagy áramsűrűségek esetén (xenon lámpa esetén: >2000 A/cm2) fontos szerephez jutnak az elektron-ion kölcsönhatások (rekombináció, ütközés) melyek a spektrum folytonos jellegét eredményezik. Ezzel szemben kis áramsűrűségek esetén a spektrum jellegében vonalas szerkezetű.
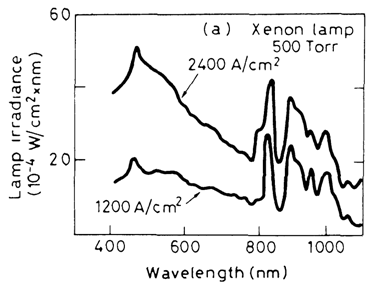
5.2. ábra. Xenon lámpa emissziós spektrumának függése az áramsűrűségtől. Növelve az áramsűrűséget a spektrum folytonos jellege kezd dominálni. Alacsonyabb áramsűrűségek esetén a spektrum jellegét tekintve vonalas szerkezetű. [5.1]
η t (transfer efficiency): A gerjesztés "geometriai" hatásfoka megmutatja, hogy a lámpa hasznos spektrális tartományba kibocsájtott fényének mekkora része jut el ténylegesen az aktív közegbe. A gyakorlatban számos geometriai elrendezés ismert, melyeket két nagy csoportba sorolhatunk. Az első megközelítésnél a lámpát vagy lámpákat olyan közel helyezik el az aktív anyaghoz, hogy azok közvetlen módon gerjesszék az aktív közeget. Ekkor a lámpa lehet pl. párhuzamos az aktív közeggel (5.3. a és b ábra), vagy spirálisan körbe is veheti azt (5.3. c ábra). A második megközelítésben a lámpa fényét optikai leképezéssel vetítik az aktív közegbe. Például ellipszis keresztmetszetű henger egyik fókuszvonalába helyezik a lámpát, míg a másik fókuszba az aktív közeget (5.3. d és e ábra) rakják. Nagyobb gerjesztő teljesítmény eléréséhez összetett, a fenti módszerek kombinálásán alapuló geometriai elrendezéseket dolgoztak ki. Az optimalizálás fontos paramétere az aktív anyag homogén gerjesztése, ami egyrészt a kialakuló lézerfény fizikai tulajdonságait, másrészt a lézer élettartalmát is nagymértékben befolyásolhatja. Optimális gerjesztés esetén a "geometriai" hatásfoka meghaladhatja a 90%-ot.
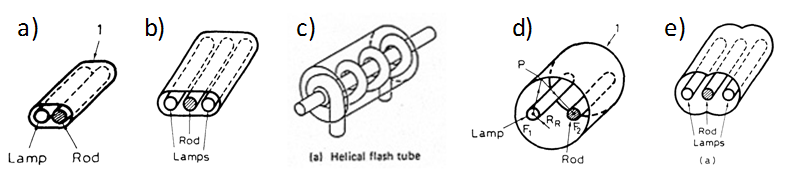
5.3. ábra. Közvetlen (a, b és c) és optikai leképezésen (d és e) alapuló pumpálási geometriák. [5.1]
η a (absorption efficiency): Az abszorpciós hatásfok megmutatja, hogy az aktív közeget elérő pumpáló fényteljesítmény hány százaléka nyelődik el. A hatásfok leginkább az aktív közeg abszorpciós és az alkalmazott lámpa emissziós spektrumainak átfedésétől függ. Ezért a nagysága erősen függ a lézer típusától; alexandritlézernél pl. meghaladhatja az 50%-ot.
η pq (power quantum efficiency): A teljesítmény kvantum hatásfok megmutatja, hogy az elnyelt teljesítmény hány százaléka fordítódik a lézerátmenet felső energiaszintjének betöltésére. Tipikus értéke 60%.
A fentiek alapján a lézerek pumpálásának eredő hatásfoka: η p = η r η t η a η pq és tipikus értéke 10% alatt van. A hatásfok ismeretében a gerjesztési ráta a fenti egyenletek segítségével számolható:
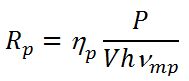 |
. | (5.4) |
Koherens optikai gerjesztés esetén az aktív anyagot lézerfény segítségével gerjesztjük és hozzuk benne létre a lézerműködéshez szükséges populáció inverziót. A lámpával való gerjesztéshez képest nagy előnye, hogy a hullámhossz alkalmas megválasztásával a pumpálás hatásfoka jelentősen növelhető. Példaként említhetőek a N2 vagy excimer lézerekkel gerjesztett festéklézerek, vagy az argon-ion lézerrel pumpált Ti:zafír lézerek. Kis méretük és nagy teljesítményük miatt azonban a diódalézerek terjedtek el a legszélesebb körben, mint pumpáló lézerek. Ezen kompakt lézerek alkalmazása gazdaságosabb, nagyobb teljesítményű és hosszabb élettartamú lézerek előállítását teszik lehetővé. A lézeres pumpálás esetén két geometriai elrendezést érdemes elkülöníteni. Longitudinális gerjesztés esetén a pumpáló nyaláb párhuzamos a lézerrel, míg tranzverzális gerjesztés esetén arra merőleges. A 5.4. a, b, és c ábrákon a longitudinális gerjesztéshez leginkább alkalmazott geometriai megoldások láthatóak.
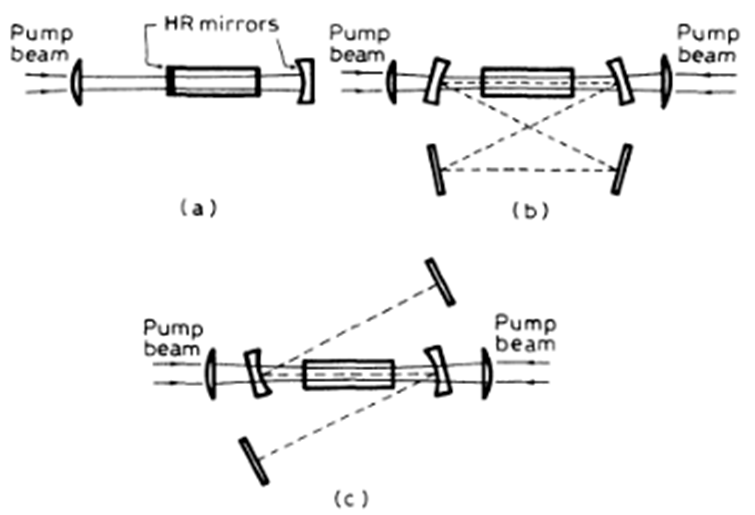
5.4. ábra. Longitudinális koherens pumpálási geometriák [5.1]
A következőkben longitudinális gerjesztést feltételezve számítjuk ki a pumpálási rátát és hatásfokot. A pumpálási ráta az aktív közeg adott (r, z) koordinátájú pontjában megadható az
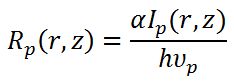
formulával, ahol Ip(r, z) a pumpáló nyaláb intenzitása, továbbá α a közeg abszorpciós együtthatója a ν p pumpáló frekvencián. Radiális irányban Gauss-os, valamint axiális irányban a Beer-Lambert törvényt követő, exponenciális gerjesztő intenzitásprofilt feltételezve írhatjuk:
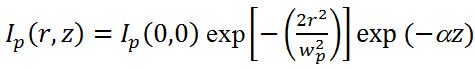 |
, | (5.5) |
ahol Ip(0,0) a belépő síkban a pumpáló nyaláb intenzitása, valamint wp a nyaláb mérete. Feltételezzük, hogy a pumpáló nyaláb átmérője állandó (wp független az axiális koordinátától) és az aktív anyag abszorpciós együtthatója nem változik meg a gerjesztés során. A belépő síkban az intenzitást kiszámíthatjuk az I(0,0)=2Ppi /πwp2 képlettel, ahol Ppi a pumpáló nyaláb teljesítménye a belépő síkban. Az emissziós- és a gerjesztés geometriai hatásfokának ismeretében a lézerműködéshez szükséges teljesítmény: Pp = Ppi/η r η t , ahonnan a fenti egyenletek alapján a gerjesztési rátára írhatjuk:
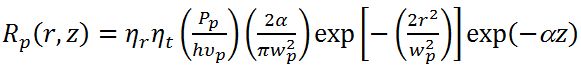 |
. | (5.6) |
Általános esetben az effektív pumpálási ráta az adott módusra számított Rp átlagos értékével adható meg:
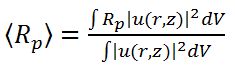 |
. | (5.7) |
ahol u(r, z) a tér amplitúdója ( E(r, z)=u(r, z) exp[-ikz] ). TEM00 módusú Gauss nyalábot feltételezve melynek w0 nyalábnyaka az aktív közegben van és a nyaláb mérete jó közelítéssel konstans (R→ ∞, φ ≈ 0) írhatjuk:
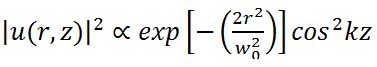 |
. | (5.8) |
Ezen egyenletet visszahelyettesítve és alkalmazva a Beer-Lambert törvényt η a =[1-exp(-αD)], továbbá kihasználva hogy a cos2kz tényező a z koordináta gyorsan változó függvénye, az effektív pumpálási rátára kapjuk:
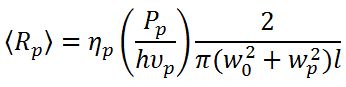 |
, | (5.9) |
ahol l az aktív közeg hossza és η p a pumpálás hatásfoka. Adott Pp pumpálási teljesítmény mellett a <Rp> effektív pumpálási ráta a pumpáló nyaláb méretének (wp) csökkentésével növelhető. A gerjesztő lézernyaláb méretének csökkentése azonban megnöveli a nyaláb divergenciáját. A gerjesztő nyaláb radiális eloszlása függeni fog az axiális pozíciótól (z koordináta) ami a levezetéskor használt közelítések érvényvesztését jelenti. A pumpáló nyaláb méretének növelése homogén gerjesztést tesz lehetővé, de csökkenti a hatásfokot. Általános szabályként megfogalmazhatjuk, hogy lézerek longitudinális koherens gerjesztésénél ideális esetben a gerjesztő nyaláb mérete közel azonos a kialakuló Gauss-nyaláb méretével wp ≈ w0 azaz a gerjesztő nyaláb és a kialakuló lézernyaláb paraméterei hasonlóak.
Négynívós rendszerben a fent kapott effektív pumpálási ráta felhasználásával - ebben a jegyzetben nem részletezett módon - megadhatjuk a lézerműködéshez szükséges pumpálási teljesítmény határértékét:
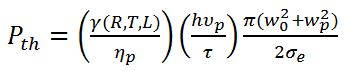 |
, | (5.10) |
ahol R, T a rezonátort alkotó tükrök reflexiós és transzmissziós tényezője, L a rezonátor belső vesztesége, τ a gerjesztett állapot élettartama és σe a kényszerített emisszió hatáskeresztmetszete. Az eredmény jól mutatja, hogy a w0 nyalábnyak növelésével a pumpálási teljesítmény határértéke megnövekszik, hiszen ekkor a módus "széle" a kevésbé gerjesztett tartományba esik.
Transzverzális gerjesztés esetén induljunk ki a pumpálási ráta és a pumpáló teljesítmény között fennálló összefüggésből:
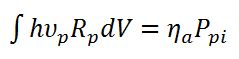 |
, | (5.11) |
ahol η a -t, azaz aktív közegben az elnyelődés mértékét a Beer-Lambert törvényből számíthatjuk ismét ki. Azonban most a képletben szereplő D paraméter a lézerrúd releváns tranzverzális mérete, legegyszerűbb esetben megegyezik a rúd DR átmérőjével. Tételezzük fel, hogy a pumpálási ráta konstans értékű (Rp = η r η t η a Pp /hνpV) az aktív anyag centrális tartományában (0 ≤ r ≤ a) és zéró (Rp = 0) a tartományon kívül (r > a). Az adott egyszerű modellben az effektív pumpálási rátára írhatjuk:
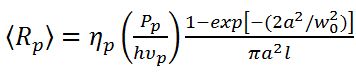 |
. | (5.12) |
Négynívós rendszer esetén is - a longitudinális gerjesztéshez hasonlóan - megadhatjuk a pumpálási teljesítmény határértékét:
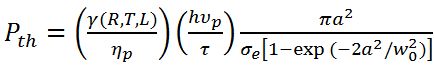 |
. | (5.13) |
A pumpálási teljesítmény határértéke ebben az esetben is növekszik a nyalábnyak növelésével, mert a keletkezett módus széle itt is a kevésbé gerjesztett (r > a) tartományba esik.
Az elektronütközéses gerjesztést elsősorban gázlézerek és félvezetőlézerek gerjesztésére alkalmazzák. Ebben a fejezetben elsősorban a gázlézerek gerjesztésével foglalkozunk. Az alkalmazott gázkisülés geometriájától függően megkülönböztetünk longitudinális és tranzverzális kisülési csöveket (lsd. 5.5. ábra). Mivel a radiális mérete a transzverzális csöveknek általában kisebb, mint a longitudinális csövek hossza, a transzverzális gerjesztés tipikusan kisebb feszültséget igényel. Azonban a longitudinális gerjesztés általában szebb nyalábprofilt eredményez.
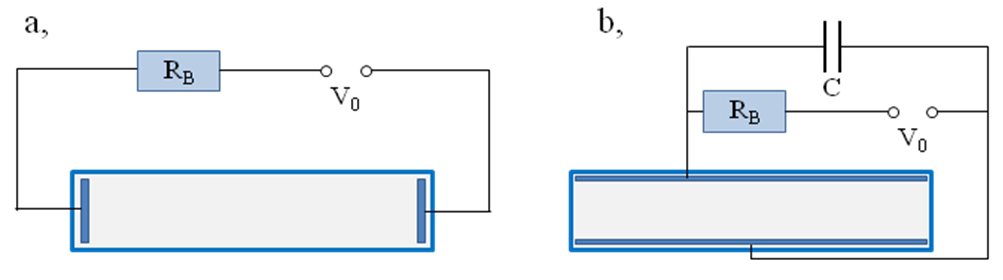
5.5. ábra. Longitudinális (a) és transzverzális (b) elektronütközéses gerjesztési módok.
Egy kisülési csőre kapcsolt egyen-, váltó- vagy impulzus-feszültség hatására, a csőben kialakuló elektromos tér gyorsítani fogja a katódból kilépő elektronokat. A felgyorsult elektronok, mozgási energiájuktól függően kölcsönhatásba lépnek a gáz molekuláival. A lézerek működése szempontjából legfontosabb kölcsönhatások a következők:
Rugalmas elektronütközés (A + e → A + e): A felgyorsult e elektronok sebessége jóval nagyobb, míg tömegük jelentősen kisebb, mint a jó közelítéssel nyugalomban lévő gázatomoké. Az elektron az A atom elektronburkának az átlagos taszító erejével lép kölcsönhatásba, sebességének lényegében nem, csak az iránya változik meg. A rugalmas ütközéskor véletlenszerű irányba szóródó elektron energiavesztesége arányos az elektron és az atom tömegeinek hányadosával: 2(m/M). Argon atom esetén pl. m/M = 1,3 10-5, azaz valóban elhanyagolható a fellépő energiaveszteség, az ütközés rugalmas.
Rugalmatlan elektronütközés (A + e → A* + e): Ha a felgyorsult elektron energiája eléri az atom külső elektronjának gerjesztési szintjét akkor rugalmatlan ütközés játszódhat le. Ennek során az elektron veszít energiájából, és az atom gerjesztett állapotba kerül. Tovább növelve az elektron energiáját, az ionizálhatja az atomot, leszakítva annak külső elektronját. Ebben az esetben a felgyorsított elektron energiája nagyobb, mint a külső elektron kötési energiája (A + e → A + + 2e). Az elektron energiájának további növelésével többszörös ionizáció érhető el, melynek során többszörösen pozitív töltésű atom keletkezik a gázban (A + e → A 2+ + 3e). A többszörös ionizációhoz szükséges energia nemlineárisan növekszik, pl. a higany gerjesztéséhez 4,88eV energia szükséges, az egyszeres ionizációhoz 10,4 eV, míg az ötszörös ionizációhoz 171 eV. Az így keletkezett pozitív ionokkal az elektronok ismét egyesülhetnek (rekombináció). Ez a folyamat az ionizáció megfordítását jelenti (A + + e → A*).
Metastabil állapotok: Az elektronütközések során olyan gerjesztett állapotok is létre jöhetnek, amelyekről csak tiltott átmenetek során lehet az alapállapotba visszajutni. Ekkor további kölcsönhatásokra (ütközés a tartály falával, másodfajú ütközés, stb.) van szükség, hogy az atom visszakerüljön alapállapotba vagy egy másik olyan állapotba, ahonnan megengedett optikai átmenettel jut alapállapotba. Ezen folyamatok a részecske mozgásával kapcsolatosak, ezért lassú, 10-2 - 10-4s ideig tartanak.
Másodfajú ütközés (A* + B → A + B*): Ezen folyamat során a gerjesztett A* részecske gerjeszti az alapállapotban lévő B részecskét, miközben ő újra A alapállapotba kerül. A folyamat akkor jelentős ha az A és B részecskék gerjesztési energiái közel azonosak. Ez a folyamat sok gázlézer esetén jelenti az alapvető gerjesztési mechanizmust (He-Ne lézer, stb.).
Fotongerjesztés (A + hν → A*): A fejezet elején ismertetett optikai gerjesztésnek megfelelő mechanizmus. Az alapállapotban lévő A atomot egy hν energiájúfoton A* gerjesztett állapotba hoz.
Elektron-elektron ütközés: A kisülési csőben még alacsony ionizáció mellett is jelentős az elektronok egymáson való szóródása. Mivel mindkét részecske töltött és tömegük azonos az ütközés során számottevő energiaváltozások léphetnek fel.
A csőben kialakuló kisülés jellege a gáz nyomásától, a csőre kapcsolt feszültségtől, a gáz fajtájától és a cső geometriai paramétereitől függ. A kisülési cső nem ohmnikus vezető, az áramerősség korlátozásához - a csővel sorosan kapcsolt - ohmnikus ellenállást kell alkalmazni. A csőre kapcsolt áram erősségének folyamatos növelésével a 5.6. ábrán látható feszültség-áram (U - I) karakterisztikát mérhetjük ki. Az U - I karakterisztika alapján három tartományt különíthetünk el. Az alacsony áramsűrűség mellett kialakuló Townsend-féle sötét kisülésben az ütközési ionizáció és tértöltés lényegében elhanyagolható szerepű. Növelve az áramsűrűséget egy átmeneti szakasz után ködfénykisülés alakul ki amelyben az ütközési ionizáció révén kialakuló tértöltések játszanak fontos szerepet. A Townsend-féle sötét kisülés egy Ugy gyújtófeszültség elérésekor megy át ködfénykisülésbe, melynek stacionárius fenntartásához egy, a gyújtófeszültségnél kisebb égési feszültségre van szükség. Paschen törvénye alapján az azonos gázzal töltött csövek gyújtófeszültsége azonos, ha a csőben uralkodó p nyomás és az elektródák d távolságának szorzata megegyezik: homogén terekben a gyújtófeszültség csak a pd függvénye. Megmutatható, hogy a gyújtófeszültségnek a pd függvényében minimuma van. Ha az elektródára kapcsolt felültség kisebb mint ez a minimum érték, akkor semmilyen p és d értéknél nem lesz kisülés a csőben. A csőre kapcsolt 100 - 300 V feszültség mellett a pd szorzat minimális értéke kb. 0,7 Pa·m. Az áramsűrűséget tovább növelve a hőmérsékleti ionizáció és a katód termikus elektronemissziója révén ívkisülés alakul ki.
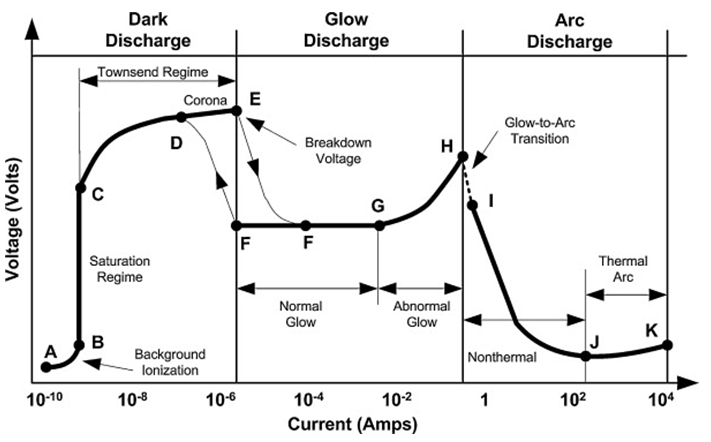
5.6. ábra. Kisülési cső áram-feszültség karakterisztikája. [5.2]
Most vizsgáljuk meg részletesebben a gázlézerek gerjesztése szempontjából is fontos ködfénykisülés keletkezését. A ködfénykisülés során a csőben jól elhatárolódó tartományok alakulnak ki (lsd. 5.5. ábra) melyek kialakulásában a ionizált pozitív töltésű és nagy tömegű ionok, továbbá az elektronok játszanak fontos szerepet. Elegendően nagy feszültség hatására a csőben lévő pozitív töltésű ionok felgyorsulnak és a katódba ütközve abból elektronokat keltenek. Ezek az elektronok a tér hatására az anód felé gyorsulnak és kellő energiát elérve ionizálják a gázt. Ez a folyamat a negatív ködfény katód felöli oldalán kezdődik. Az ionizált atomok gyorsulva indulnak a katód felé, ahonnan újabb elektronokat váltanak ki. Mivel a keletkezett ionok tömege jelentősen nagyobb mint az elektronok tömege, az ionok kisebb sebességgel mozognak és így pozitív tértöltés alakul ki a negatív ködfényben (különösen annak a katód felöli oldalán). Ezen pozitív tértöltés az oka a negatív katód és a negatív ködfény között lévő nagy feszültségesésnek (katódesés). A katódesés fontos szerepet játszik a stacionárius ködfénykisülés fenntartásában, hiszen ezáltal gyorsulnak fel a pozitív töltésű atomok, melyek a katódba ütközve újabb elektronokat keltelen. Továbbá ebben a térben gyorsulnak fel a keltett elektronok is, hogy a negatív ködfényben, már kellő energiával rendelkezve ionizálják a gázt. Az ionizáció során lelassult illetve az ott keletkezett elektronok energiája még túl alacsony, ezért nem tudják gerjeszteni a gázt (Faraday-féle sötét tér). Az ionizációhoz szükséges energiára csak a pozitív oszlopot elérve tesznek szert. A pozitív oszlopban a potenciálesés egyenletes ami arra utal, hogy nem alakul ki tértöltés, a pozitív és negatív töltések sűrűsége azonos. Az ilyen - erősen ionizált - gázt plazmának nevezzük.
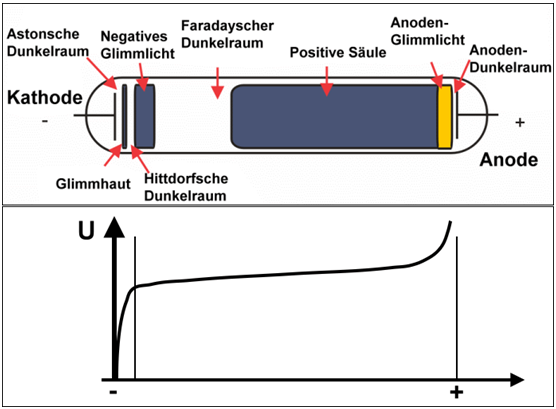
5.7. ábra. Ködfénykisülés (a) során a kisülési csőben megfigyelhető tartományok és a cső mentén mérhető feszültségesés (b) [5.3]
A ködfénykisülés bizonyos tartományában a növekvő áramerőséggel a feszültség csökken, amely karakterisztika az ívkisülésnél is megfigyelhető. Ez azt jelenti, hogy az I áramerősség növelésével a cső ellenállása (R = U/I) csökken. Ezen karakterisztika miatt a kisülés stacionárius jellegének megőrzéséhez a csővel sorosan egy előtét-ellenállást kell kapcsolni (RB a 5.5. ábrán). Ekkor a csőre eső feszültség U = U0 - I·RB növekszik illetve csökken az áramerősség nagyobb illetve kisebb értéke mellett. Ezen egyszerű kapcsolás stabilizálja a kisülést és biztosítja a gázlézerek stacionárius gerjesztését.
A lézerek gerjesztése szempontjából azok a gerjesztési mechanizmusok az elsődlegesen fontosak, amelyek a gázrészecskéket a lézerműködéshez szükséges gerjesztett állapotba hozzák. A legegyszerűbb esetben képzeljünk el egy kollimált monokromatikus (az elektronok energiája azonos) elektronnyalábot és haladjon keresztül egy olyan gázon melynek a teljes hatáskeresztmetszete σ e . Ekkor egy dz távolságú gázrétegen áthaladva az elektronnyaláb Fe fluxusa lecsökken: dFe = -σe Nt Fe dz, ahol Nt a részecskék teljes számát jelöli. Azon ütközések amelyek a gázmolekulákat ténylegesen a lézerátmenet felső energiaszintjére gerjesztik nagyon ritkák, a hozzá tartozó σe2 hatáskeresztmetszet jóval kisebb mint pl. a rugalmas ütközéshez tartozó σel ~ 10-16 cm2 érték. A gerjesztett állapot populációs rátája:
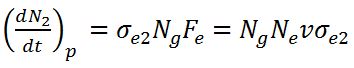 |
, | (5.14) |
ahol v az elektron sebessége és Ne az elektron sűrűség. A valóságban a σ e 2 hatáskeresztmetszet függ az elektron energiától ezért a gerjesztett állapot populációs rátájára írhatjuk, hogy:
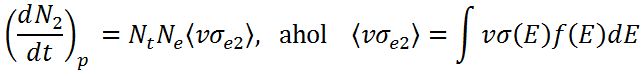 |
, | (5.15) |
és f(E) az elektronok energiaeloszlását adja meg. Ezek alapján a pumpálási rátára kapjuk:
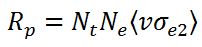 |
. | (5.16) |
A pumpálási ráta megadásához tehát ismernünk kell a hatáskeresztmetszet σ e 2(E) energiafüggését és a kisülési csőben lévő elektronok f(E) energiaeloszlását. A hatáskeresztmetszet egy jól meghatározott küszöbbel rendelkezik, amelynek értéke közel egyenlő az átmenethez tartozó energiával. A foton abszorpciós hatáskeresztmetszetéhez képest széles spektrumú, mert az elektronütközéses gerjesztés lényegében egy nem-rezonáns folyamat. Mindezek következtében a gázok jó hatásfokkal gerjeszthetőek polikromatikus elektronnyalábokkal. Az elektronok energia eloszlását a Maxwell-Boltzmann eloszlással írhatjuk le:
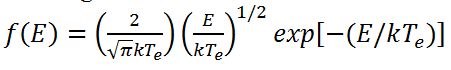 |
, | (5.17) |
ahol Te az elektron hőmérséklete. Ezért az elektronok energia eloszlásához elegendő ismernünk az elektronok Te hőmérsékletét:
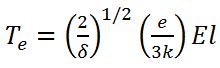 |
, | (5.18) |
ahol δ a veszteségi tényező, E az elektromos térerősség és l az elektronok közepes szabad úthossza. Mivel az elektronok szabad úthossza fordítottan arányos a p nyomással, az elektronok hőmérséklete arányos lesz E/p hányadossal. A fentieknél pontosabb számításokkal megmutatható, hogy az elektronok hőmérséklete nem egyszerűen arányos, hanem összetett függvénye az E/p hányadosnak: Te= f(E/p). Ezért az E/p hányados egy, a kisülési cső jellemzésére alkalmas alapvető mennyiség. Adott gázkeverék mellett általában létezik egy olyan E/p hányados, ami mellett a pumpálási ráta maximális. Alacsony E/p hányados mellett túlságosan alacsony az elektrongáz hőmérséklete a lézer jó hatásfokú gerjesztéséhez. Másrészt a hányados magas értéke mellett magas - a lézerműködéshez szükségtelen - energianívók gerjesztődnek, vagy ionizálódhatnak a molekulák instabillá téve a gázkisülést (pl. a ködfénykisülés tartományából átmegy ívkisülés tartományába).
Az áramsűrűség J = evdrift Ne (ahol vdrift = < vz >=(δ/2)1/4(eE/m)1/2) ismeretében a pumpálási rátára írhatjuk, hogy
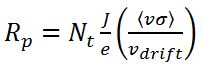 |
. | (5.19) |
Az elektronok energia eloszlását Maxwell-féle eloszlásnak feltételezve a <vσ> tényező csak a Te hőmérséklettől függ. A nevezőben szereplő vdrift szintén csak a Te függvénye. Egy adott p nyomáson és R csőrádiusz esetén a hőmérséklet állandó marad, ideális esetben közel a lézer optimális üzemi értékéhez. Ebből következően a pumpálási ráta kifejezésében a zárójeles tényező egy konstans, független az áramsűrűségtől. Azaz ebben az egyszerű modellben a pumpálási ráta egyenesen arányos az áramsűrűséggel. A korábbiakhoz hasonlóan definiálhatjuk a pumpálás hatásfokát is:
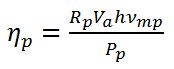 |
, | (5.20) |
ahol Va az aktív anyag térfogata.
Meg kell jegyeznünk, hogy sok esetben a fenti egyenletek erősen közelítő jellegűek, inkább kvalitatív mint kvantitatív számolásokhoz használhatóak. Az elektronok energia eloszlására alkalmazott Maxwell-Boltzmann eloszlás csak durva közelítés, a gyakorlatban a valós eloszlás ettől jelentősen eltér.
A lézerek optimális gerjesztésére számos elektromos kapcsolást fejlesztettek ki (Blümlein, charge transfer, haladó hullámú, spiker sustainer stb.). Itt csak az egyik legegyszerűbb pl. a nitrogén lézerek gerjesztése alkalmas Blümlein-kapcsolást ismertetjük részletesebben.
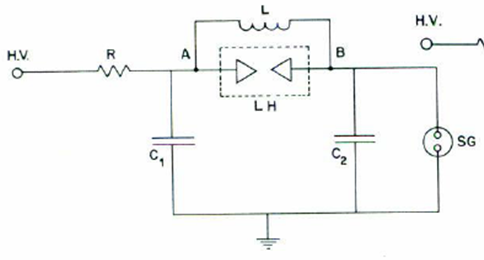
5.8. ábra. Blümlein kapcsolás
A Blümlein kapcsolás sematikus vázlata a 5.8. ábrán látható. A két, C1 és C2 kapacitások az L tekercsen keresztül egymással párhuzamosan vannak összekapcsolva. A kapcsolási rajzon LH a lézert (laser head) és SG a szikraközt (spark gap) jelöli. A kezdeti állapotban mindkét földelt kapacitás azonos feszültségre van feltöltve. Ugyanekkora feszültség esik a szikraközre is, de a lézer kisülési csövén a feszültség zéró. Amikor a szikraközön a feszültség meghaladja a rá jellemző átütési feszültséget (U0) a C2 kapacitás kisül. A C1 kapacitás egy ideig még töltve marad, mert a C1 kisülése olyan gyors, hogy az L tekercs impedanciája késlelteti a C1 kisülését. A C2 kisütésével a B pontban leesik a feszültség és a lézer feszültség alá kerül. Mivel ez az áramkör egy feszültség kétszerező áramkőr, a kialakuló maximális feszültség 2U0. Ez az érték azonban általában nagyobb mint a kisülési csőre jellemző gyújtási feszültség, így a csövön soha nem esik a maximális 2U0 feszültség.
Sorolja föl a lézerek eredő hatásfokát meghatározó négy tényezőt.
Hasonlítsa össze az inkoherens, és a koherens optikai gerjesztési módokat!
Elektronütközéses gerjesztés esetén adja meg, és jellemezze a lézerek működése szempontjából legfontosabb kölcsönhatásokat!
Rajzolja föl, és elemezze a Blümlein kapcsolást!
Tartalom
A fejezet első részében megvizsgáljuk, hogy milyen feltételek szükségesek a stabil, folytonos lézerműködés (continuous wave, cw) megvalósításához három- és négyszintes lézerek esetén. A tárgyaláshoz egy egyszerű modellt használunk, mely szerint a lézer egyetlen módusban működik, a pumpálási teljesítmény és a módus energiasűrűsége pedig egyenletesen oszlik el a teljes aktív közegben. Ez utóbbi azt jelenti, hogy a módus transzverzális profilja négyszög alakú (top-hat) és eltekintünk a módus állóhullám jellegétől is, mely a populációinverzió és az erősítés térbeli modulációjához vezetnek (spatial hole-burning). Habár ez a meglehetősen leegyszerűsített modell csak az egyirányú gyűrű-lézerek (unidirectional ring laser) esetén teljesülhet, a belőle levonható következtetések segíthetnek megérteni a lézerműködés alapvető jellemzőit. A fejezet további részei röviden bemutatják, miként lehet megvalósítani az egymódusú lézerműködést és hogyan stabilizálható a működési hullámhossz.
A legelterjedtebb lézertípusok nagy részének működése négyszintes sémán alakul. Ilyenek például a Nd:YAG, He-Ne, Ar-ion és nitrogén lézerek. Tekintsük a 6.1. ábrán látható négyszintes termsémát, mely szerint az 0-ás energiaszintről Rp pumpálási sebességgel gerjesztjük az atomokat a 3-as szintre, ahonnan gyors relaxációval a nagy átlagos élettartammal rendelkező 2-es szintre kerülnek. Az indukált emisszió a 2-es és 1-es szintek között megy végbe. Az 1-es szinten levő atomok gyors relaxációval a 0-ás energiaszintre kerülnek.
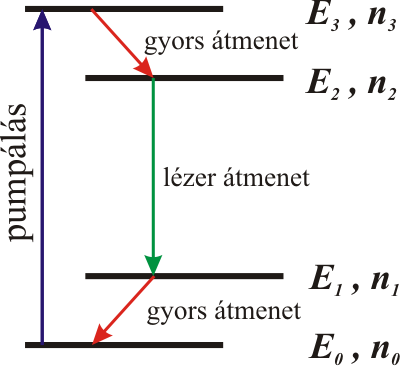
6.1. ábra. A négyszintes lézer termsémája.
Ha feltételezzük, hogy az átmenetek mindig csak a szomszédos energiaszintek között megengedettek (kivéve a pumpálást) akkor az adott rendszerre a populációegyenletek a következők lesznek:
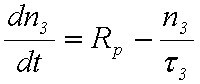 |
. | (6.1) |
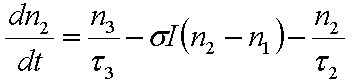 |
, | (6.2) |
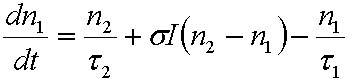 |
, | (6.3) |
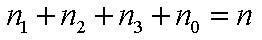 |
. | (6.4) |
Négyszintes rendszerben a lézerműködés során a felsőbb energiaszinteken levő atomok száma elhanyagolható a teljes n atomszámhoz (koncentrációhoz) és az alapszinten levő atomok n0 számához képest, vagyis a 0-s energiaszint egy "tartály" szerepét tölti be. Közelítések alkalmazásával a populációegyenletek jelentősen leegyszerűsíthetők. Mivel a 3-as energiaszinten az élettartam nagyon rövid, feltételezzük, hogy ez a szint állandóan üres, a pumpálással gerjesztett atomok gyakorlatilag azonnal a 2-es szintre kerülnek:
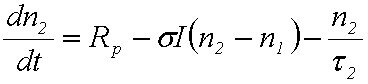 |
, | (6.5) |
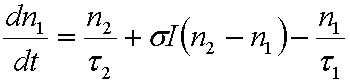 |
. | (6.6) |
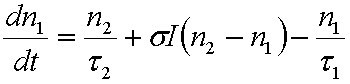 |
. | (6.7) |
Figyeljük meg, hogy kisjelű lézerintenzitás (itt fotonintenzitás: foton/(cm2s) ) ( I ≈ 0) és egyensúly esetben a (6.6) egyenlet alapján n2/τ2 = n1/τ1. Ez alapján a populációinverzió (Δn = n2 - n 1 > 0) megvalósíthatóságnak egyetlen feltétele, hogy
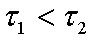 |
. | (6.8) |
Ez esetben a populáció inverzió bármilyen kis pumpálási sebesség esetén megvalósul és a közeg erősítőként fog viselkedni. Ha viszont a (6.8) feltétel nem teljesül, akkor az adott négyszintes rendszer csak impulzus üzemmódban működhet, feltételezve, hogy a gerjesztés időtartama rövidebb, mint a 2-es szint átlagos élettartama. Ilyenkor a kezdeti populációinverzió megszűnését az indukált emisszió okozza, ezért az ilyen lézertípusokat önkioltó lézereknek nevezik.
A következőkben vizsgáljuk azt az esetet, amikor τ1 << τ 2 . Ebben az esetben n1 ≈ 0, vagyis Δn ≈ n2, ami a (6.5-7) egyenletrendszer további egyszerűsödéséhez vezet:
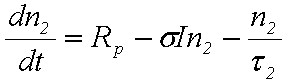 |
. | (6.9) |
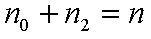 |
. | (6.10) |
Ezen két egyenletet kiegészíti az intenzitás időbeni változását leíró tag. A rezonátorban a két egymással szemben haladó I+ és I- összege adja ki a helyi összintenzitást, melyet jó közelítéssel azonosnak tekinthetünk az erősítésben résztvevő teljes térfogatban. Mivel a spontán emisszióból származó fotonok hozzájárulását elhanyagolhatjuk, a fotonintenzitás változása csak a 2-es és 1-es szintek közötti indukált emisszió, valamint a rezonátorban fellépő, τc átlagos foton-élettartammal jellemezhető veszteségek együttes hatásából adódik. Ez alapján 1-es törésmutatót feltételezve:
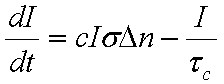 |
. | (6.11) |
Nyilvánvaló, hogy a spontán emissziót nem tartalmazó egyenlet a lézerműködés kezdetére nem lehet érvényes, hiszen I = 0 esetén dI/dt = 0, azaz az egyenlet szerint a lézerműködés nem indulna be. Amennyiben a pumpálással populációinverziót hozunk létre, a spontán emisszió során kibocsátott kevés számú foton által képviselt gyenge intenzitás (I > 0) az aktív közegben haladva erősödni fog. Ahhoz, hogy a stabil lézerműködés beinduljon (dI/dt > 0) szükséges, hogy a rezonátorban egy teljes körüljárás ideje alatt az erősítés legalább akkora legyen, mint a rezonátorban fellépő veszteségek, azaz
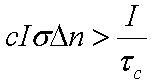 |
. | (6.12) |
Innen a küszöbfeltételhez tartozó Δnc kritikus populációinverzió:
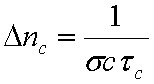 |
. | (6.13) |
A kritikus populációinverzió a stabil lézerműködés feltétele, ennek értéke független az aktuális intenzitástól. Az eléréséhez szükséges legkisebb, kritikus pumpálási sebességet megkaphatjuk a dn2/dt = 0 egyensúlyi feltételből kisjelű (I ≈ 0) erősítés esetén. Felhasználva, hogy Δn = n2 - n1, a (6.9) és (6.10) egyenletekből kapjuk, hogy:
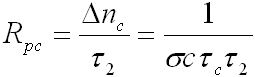 |
. | (6.14) |
Láthatjuk, hogy minél kisebb a rezonátor vesztesége és minél nagyobb a 2 → 1 spontán átmenetet jellemző élettartam, annál kisebb a lézerműködés beindításához szükséges pumpálási sebesség. Ha megnöveljük a pumpálási sebességet majd állandó értéken tartjuk, akkor egy stabil intenzitás érték fog kialakulni. Ennek értékét úgyszintén a dn2/dt = 0 és dI/dt = 0 egyensúlyi feltételek alapján kapjuk meg:
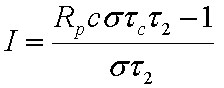 |
. | (6.15) |
Felhasználva a (6.14) egyenletet és figyelembe véve, hogy a nevező a telítési intenzitás reciproka, a fenti összefüggés ez meglehetősen egyszerű és szemléletes alakban írható fel:
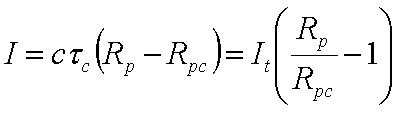 |
. | (6.16) |
A kapott eredményeket a 6.2. ábra segítségével foglalhatjuk össze. Ha a pumpálási sebességet 0-ról növelni kezdjük, a stacionárius állapotra érvényes populációinverzió lineárisan növekedni kezd, míg el nem éri a Δnc kritikus értéket. Ekkor beindul a lézerműködés, a fotonintenzitás a pumpálási sebesség lineáris függvénye lesz, miközben a populáció-inverzió értéke állandó marad.
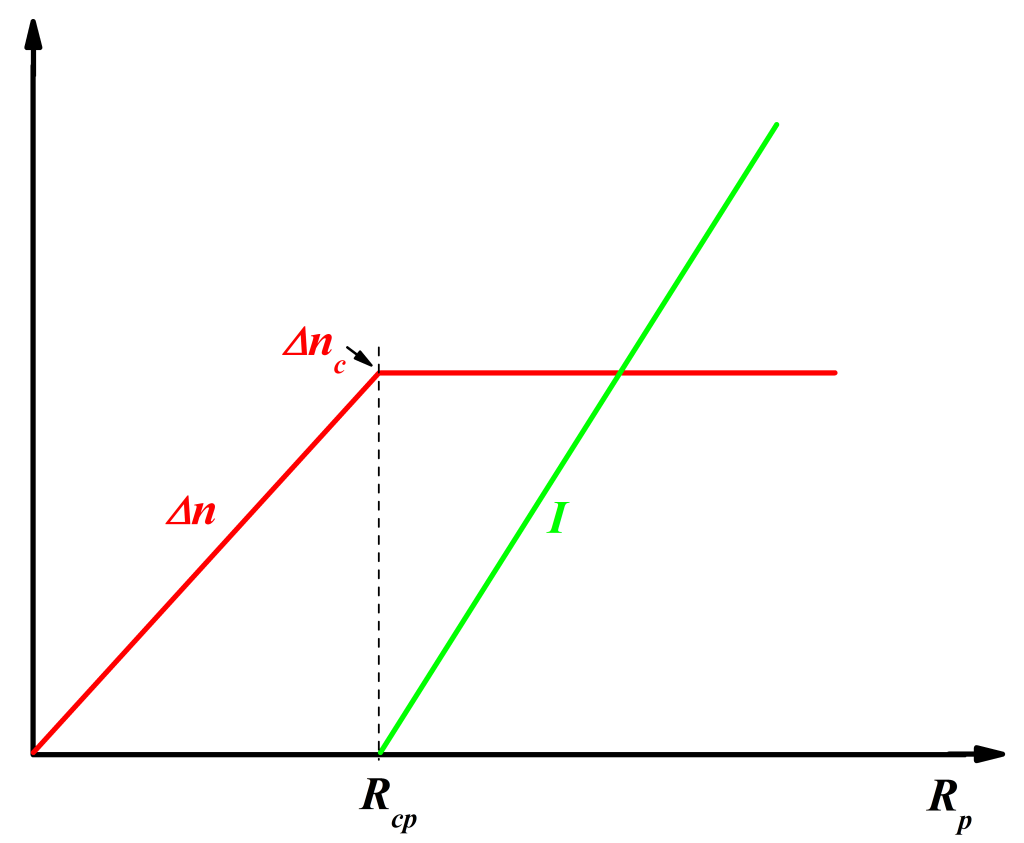
6.2. ábra. A populációinverzió és a lézerintenzitás függése a pumpálási sebességtől négyszintes lézer esetén.
A továbbiakban vizsgáljuk meg két könnyen mérhető mennyiség, a pumpálási teljesítmény és a lézer kimeneti teljesítménye közötti összefüggést. Első lépésként térjünk vissza a (6.11) egyenletben található rezonátor fotonélettartam paraméterhez. Az 1. fejezetben bemutatott egyszerű lézermodell (1.8. ábra) vizsgálatakor feltételeztük, hogy a rezonátorban az aktív közeg egy α (=σΔn) erősítési tényezővel rendelkező foton-forrás, míg a fotonszám csökkenése a tükrök nem tökéletes reflexiójából adódik. A fotonszám csökkenéséhez ezeken kívül hozzájárulhat a tükrök véges mérete, az aktív közeg határfelületén történő reflexió, szóródás, a rezonátorban levő egyéb optikai elemek (pl. Fabry-Perot interferométer). Legyen a rezonátorban adott pillanatban Nf számú foton. Ha az aktív közegben 0 az erősítés (n2 = n1) akkor a rezonátor belsejében egy teljes kör megtétele után a veszteségek miatt a fotonszám ΔNf étékkel csökkenni fog. Mivel folytonos üzemmódú lézerek esetén a veszteség és a Δt körbefutási idő kicsi, a változás differenciál alakba is írható, azaz
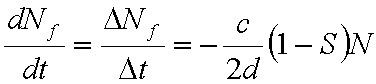 |
, | (6.17) |
ahol d a rezonátor optikai úthossza és S az egy teljes körbefutáshoz tartozó túlélési arány (1-S pedig az arányos veszteség). Ebből a rezonátor átlagos fotonélettartamára a következő összefüggés adódik:
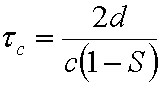 |
. | (6.18) |
Térjünk vissza a pumpálási és kimeneti teljesítmény közötti összefüggés kérdésére. Tételezzük fel, hogy adott egy A keresztmetszetű aktív közeg, mely teljesen kitölti a rezonátor tükrök közötti térrészt. Ha a közeg törésmutatója 1 (gázlézerekre jellemző érték) akkor az aktív közeg geometriai hossza megegyezik a rezonátor tükrei közötti d optikai úthosszal. Ha a teljes közeg térfogatát egyenletesen pumpáljuk, akkor a pumpálási sebesség és a P pumpálási teljesítmény között a (optikai és elektromos pumpálás esetén) következő lineáris összefüggés áll fen:
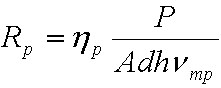 |
, | (6.19) |
ahol ηp a pumpálás hatásfoka és hνmp pedig a pumpálásban résztvevő szintek közötti energiakülönbség (lásd 5. fejezet). Ha a lézernyaláb keresztmetszete Ab és a kicsatoló tükör transzmissziója T2 akkor a lézer kimeneti teljesítménye:
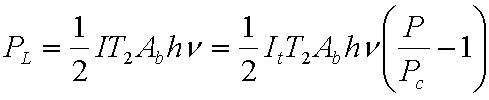 |
, | (6.20) |
ahol Pc a kritikus pumpálási sebességhez tartozó (kritikus) pumpálási teljesítmény. Az 1/2 szorzótényezőre azért van szükség, mert a I intenzitás tartalmazza az egy időben egymással szemben haladó I+ és I- összetevőket. Hasonlóan a pumpálási sebességtől való függéshez, a lézerműködés a Pc pumpálási teljesítménynél indul be, majd a P növelésével lineárisan növekszik. A függvényt az ηsdifferenciális meredekséggel (slope efficiency) jellemzik:
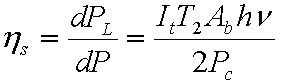 |
. | (6.21) |
A (6.14), (6.18) és (6.19) összefüggések felhasználásával a kritikus pumpálási teljesítményre kapjuk, hogy
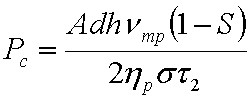 |
, | (6.22) |
melyet felhasználva a (6.21) összefüggés a következőképpen alakul:
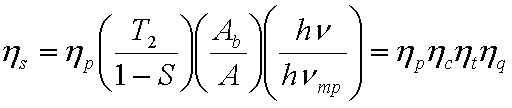 |
. | (6.23) |
A fenti egyenletben jól látszik, hogy a differenciális meredekség különböző hatásfok típusú mennyiségek szorzataként írható fel. Az ηc mennyiséget kicsatolási hatásfoknak nevezik (output coupling efficiency) és megadja, hogy a keltett lézerfotonok mekkora részarányát csatoljuk ki a rezonátorból lézernyaláb formájában. Az ηt transzverzális hatásfok megmutatja, hogy a pumpált aktív közeg keresztmetszetének mekkora részét fedi le a lézernyaláb, azaz mennyi az erősítésre hasznosított keresztmetszett. Az ηq lézer kvantum hatásfok (laser quantum efficiency) a minimális pumpálási energiának a lézer energiává alakuló hányadát adja meg.
Amint a (6.20) egyenlet is mutatja, a kicsatoló tükör transzmissziója nagymértékben befolyásolja a kimenő lézernyaláb teljesítményét. A transzmisszió változtatásával két egymással ellentétes folyamat fejti ki a hatását. Ha T2 nő, akkor megnöveljük a rezonátort elhagyó fotonok részarányát, ami a látszólag a kimeneti teljesítmény növekedését eredményezné. Ugyanakkor a megnövekedett kicsatolás növeli a rezonátor veszteségét és ezáltal a rezonátorban levő fotonok számát. Ez utóbbi hatást a (6.20) egyenletben a Pc tényező tartalmazza, melynek értéke fordítottan arányos a rezonátor élettartammal. Az optimális kicsatolás mértékét adott P pumpálási teljesítmény esetén a dPL/dT2=0 feltételből tudjuk kiszámítani a (6.21) egyenlet alapján. Hozzuk az egyenletet olyan formára, mely expliciten tartalmazza a teljes T2 függést. Ehhez válasszuk külön a kicsatoló tükör okozta veszteségeket a rezonátor többi komponensein bekövetkező veszteségtől a következő módon:
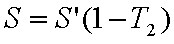 |
, | (6.24) |
ahol S' a fotonok túlélési aránya T2 ≈ 0 esetén. Ha a nulla kicsatoláshoz tartozó kritikus pumpálási teljesítményt (mely kísérletileg is meghatározható) Pc0-val jelöljük, akkor fennáll a következő összefüggés:
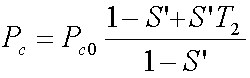 |
, | (6.25) |
melyet behelyettesítve a (6.21) egyenletbe és bevezetve az
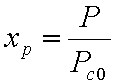 |
(6.26) |
jelölést, a kimenő lézerteljesítmény T2 függését a következő összefüggés adja meg:
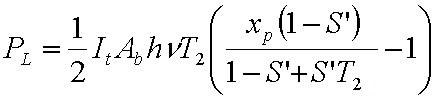 |
. | (6.27) |
Kiszámolható, hogy a PL függvény T2 szerinti deriváltja akkor zérus, ha
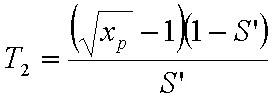 |
, | (6.28) |
melyet visszahelyettesítve a (6.27) egyenletbe megkapjuk a lézerteljesítmény maximális értékét:
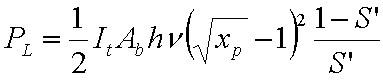 |
. | (6.29) |
A 6.3. ábra két példát mutat be a kimeneti kicsatolás és a kimeneti teljesítmény közötti összefüggésre P/Pc0 = 5 és S' = 0,90 valamint S' = 0,95 esetén. Jól látható, hogy minél nagyobb a rezonátor veszteség annál nagyobb kicsatolási aránynál érhető el az optimális kimeneti teljesítmény.
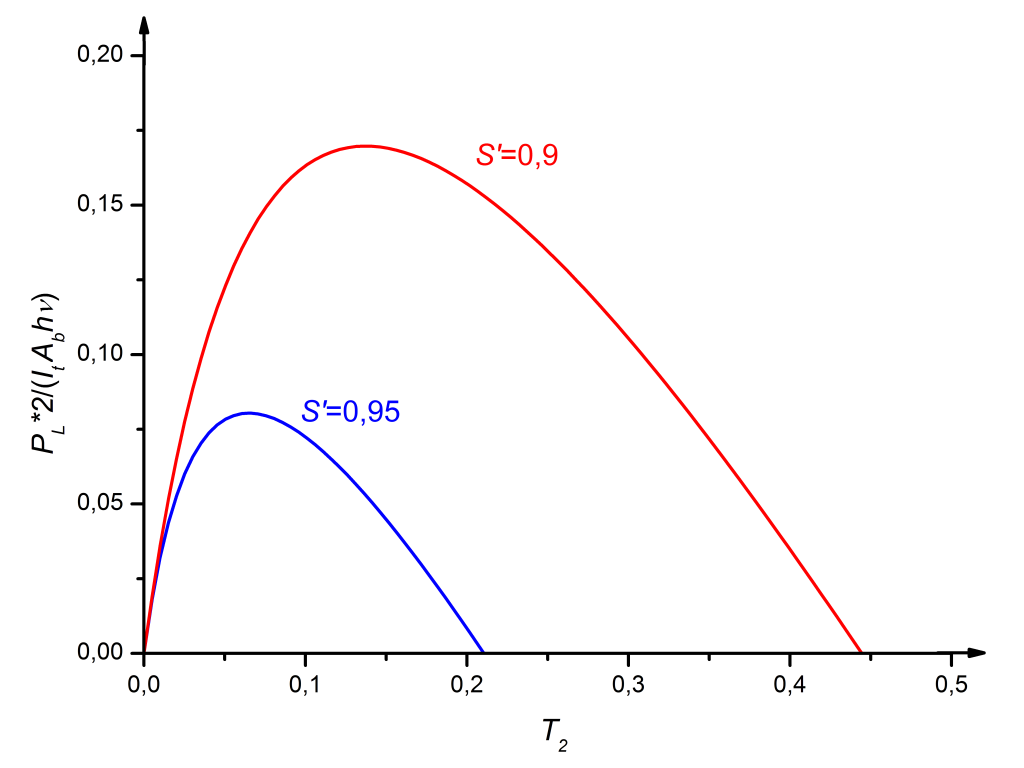
6.3. ábra. A lézer kimeneti teljesítményének függése a kicsatoló tükör transzmissziójától különböző értékű (T2 nélküli) rezonátor veszteségek esetén.
A legelső megépített lézer, a rubin lézer (Cr3+:Al2O3) háromszintes lézer volt, de ilyen gerjesztési sémán alapszik rézgőz és a CO2 lézer működése is. A háromszintes lézereknek egy kis csoportjában a pumpálás a 0-s szintről a 2-es energianívóra történik (6.4.a ábra), a lézerátmenet pedig a 2-es és 1-es szint között van. Az ilyen rendszer viselkedése leginkább a négyszinteshez hasonlít τ3=0 esetén. A legjellemzőbb háromszintes működési séma esetén az 1-es energiaszintről gerjesztjük az atomokat a 3-as szintre, ahonnan gyors relaxációval a nagy átlagos élettartammal rendelkező 2-es szintre kerülnek (6.4.b ábra). Belátható, hogy mivel ebben az esetben hiányzik a "tartály" szerepét betöltő 0-s szint, pumpálás hiányában gyakorlatilag minden atom a lézerátmenet alsó szintjén található. Ahhoz, hogy populáció inverziót hozhassunk létre, legoptimálisabb esetben is legalább az atomok felét kell egyidőben gerjesztett állapotban tartani.
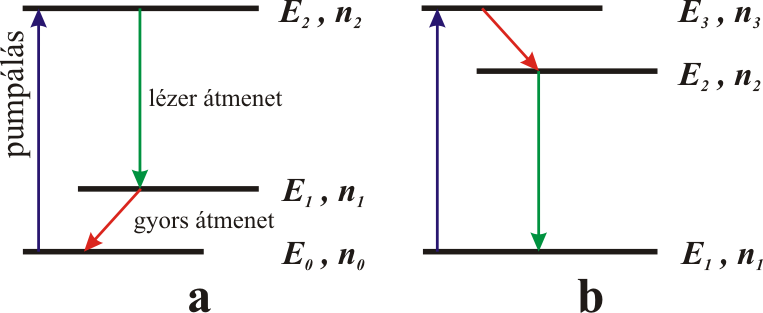
6.4. ábra. Háromszintes lézerműködési termsémák.
Vizsgáljuk meg részletesebben a 6.4.b ábrán látható rendszer működését. A populációegyenletek a következők lesznek:
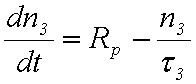 |
, | (6.30) |
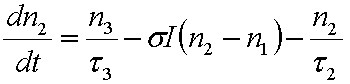 |
, | (6.31) |
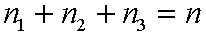 |
. | (6.32) |
Közelítések alkalmazásával a populációegyenletek jelentősen leegyszerűsíthető. Mivel a 3-as energiaszintet úgy választják meg, hogy az élettartam nagyon rövid legyen, feltételezzük, hogy ez a szint állandóan üres (optimális eset), a pumpálással gerjesztett atomok gyakorlatilag azonnal a 2-es szintre kerülnek:
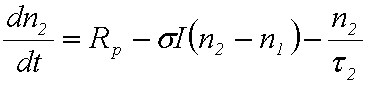 |
, | (6.33) |
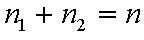 |
. | (6.34) |
Az intenzitás időbeni változását leíró tag ugyanaz lesz, mint a négyszintes lézer esetén részletesebben tárgyalt egyenlet, a küszöbfeltételeket is ugyanazt a gondolatmenetet követve határozzuk meg:
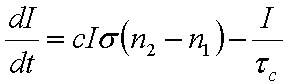 |
. | (6.35) |
A dI/dt = 0, valamint a dn2/dt = 0 egyensúlyi feltételek alapján és felhasználva, hogy n2 = (n + Δn)/2, a lézerműködés beindításához szükséges kritikus populációinverzióra és a hozzá tartozó pumpálási rátára kapjuk, hogy:
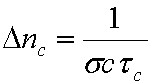 |
, | (6.36) |
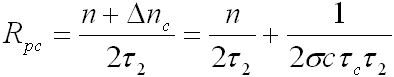 |
. | (6.37) |
Összehasonlítva a fenti eredményt a négyszintes lézernél kapott egyenlettel a legszembetűnőbb eltérés az n/(2τ2) tag megjelenése, amely a 2-es energiaszintről a teljes atomszám felét kitevő populáció spontán emisszió általi veszteségét jelenti, amelyet pumpálással folyamatosan pótolni kell. Amellett, hogy ez jelentősen megnöveli a pumpálás kritikus értékét, jelentőssé teszi a rezonátorban az erősített spontán emissziót.
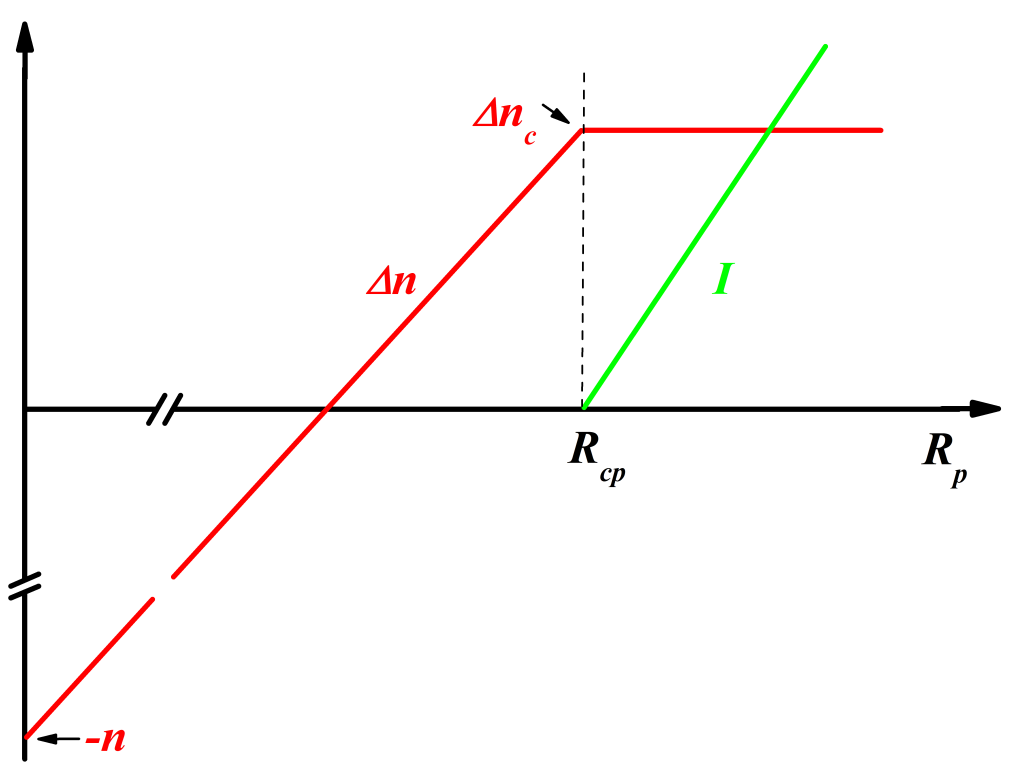
6.5. ábra. A populációinverzió és lézerintenzitás függése a pumpálási sebességtől háromszintes lézertípus esetén.
A rezonátorban adott pumpálási sebesség esetén beálló egyensúlyi intenzitásra a (6.33) összefüggésből a következőt kapjuk:
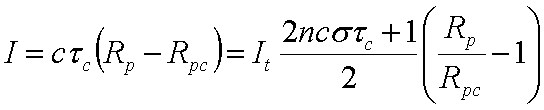 |
. | (6.38) |
A fenti összefüggés szerint annak ellenére, hogy az Rpc összefüggés eltérő a három és négyszintes lézerműködés esetén, az intenzitás pumpálási sebesség függésének meredeksége azonos, csak a rezonátor fotonélettartama határozza meg.
A négyszintes lézernél részletesebben leírt pumpálási modell alapján a szükséges számítások elvégzésével a kimeneti lézerteljesítmény és pumpálási teljesítmény közötti összefüggés az alábbi lesz:
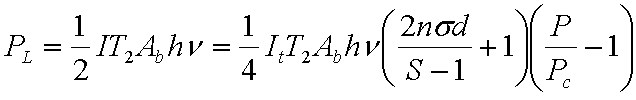 |
. | (6.39) |
A kimeneti teljesítmény differenciális meredekségét kiszámolva ez az eredmény megegyezik a négyszintes lézernél kapott értékkel. Ez első látásra ez furcsának tűnhet a nagy alapszinti abszorpció miatt, azonban az abszorpció és indukált emisszió közötti egyenleg csak a Δn populációkülönbség mértékétől függ, nem pedig a szintek betöltöttségétől.
A kvázi-háromszintes lézerek tulajdonképpen egy átmenetet képeznek a három- és négyszintes lézerek között, melyben a lézerátmenet alsó energiaszintje (1-es) az 0-s alapszint egy alszintjét képezi (6.6. ábra). Ennek következtében a két alsó szint erősen csatolt, termikus egyensúlyban vannak egymással, a betöltöttségük Boltzman eloszlás szerinti. Legyen a 0-s és 1-es szint össz-populációja n1. Mivel az E1 - E0 különbség összemérhető kT-vel, az 1-es szinten mindig jelen lesz a n1 populációnak egy bizonyos konstans értékű hányada (jelöljük fn1-gyel). A kvázi-háromszintes lézerek közzé tartozik például a 946 nm hullámhosszon működő Nd:YAG lézer, vagy az itterbium és erbium dópolt lézerek
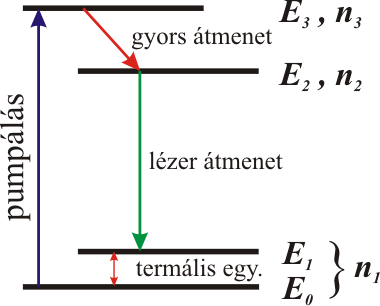
6.6. ábra. A kvázi-háromszintes lézer termsémája.
Az előző esetekhez hasonlóan feltételezve, hogy a 3-as szintre pumpált atomok elhanyagolható időn belül a 2-es szintre kerülnek, a populációegyenletek és az intenzitásváltozást leíró összefüggés a következőképpen alakulnak:
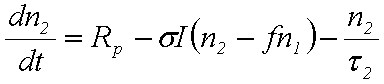 |
, | (6.40) |
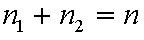 |
, | (6.41) |
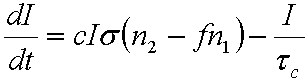 |
. | (6.42) |
A megfelelő számítások elvégzésével a kritikus pumpálási sebességre a következő összefüggést kapjuk:
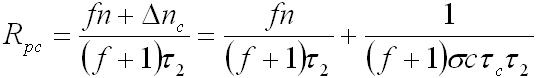 |
. | (6.43) |
Jól látszik, hogy f = 0 esetén megkapjuk a négyszintes (6.14), f = 1esetén pedig a háromszintes rendszerre (6.37) kapott kritikus pumpálási sebességet. Mivel általában f << 1, a kritikus pumpálási sebesség lényegesen alacsonyabb, mint háromszintes termséma esetén, a lézerintenzitás pumpálás-függésének meredeksége megegyezik az előző modellek esetén kapottakkal.
Bizonyos lézerek esetén (pl. CO2, Ar-ion) több lézer-átmenet is létezhet, melyek közül általában a legnagyobb erősítéssel rendelkező átmenetet használják, azonban előfordulhat, hogy igény lenne valamely másik átmeneten használni a lézert. Egyes lézertípusok pedig nagy sávszélességgel rendelkeznek (pl. festék lézerek) és bizonyos alkalmazásokhoz szükség lehet a lézerek hangolása. Ilyen esetekben meg kell növelni a rezonátor veszteségét az elnyomni kívánt hullámhosszakon, melyhez egy hullámhossz szelektív elemet építenek be a rezonátorba. Távoli- és közép infravörös tartományon egy reflexiós diffrakciós rácsot alkalmaznak ún. Littrow elrendezésben (6.7.a ábra) és a rács forgatásával választható ki az a hullámhossz, amelyet a rács visszatükröz a rezonátorba.
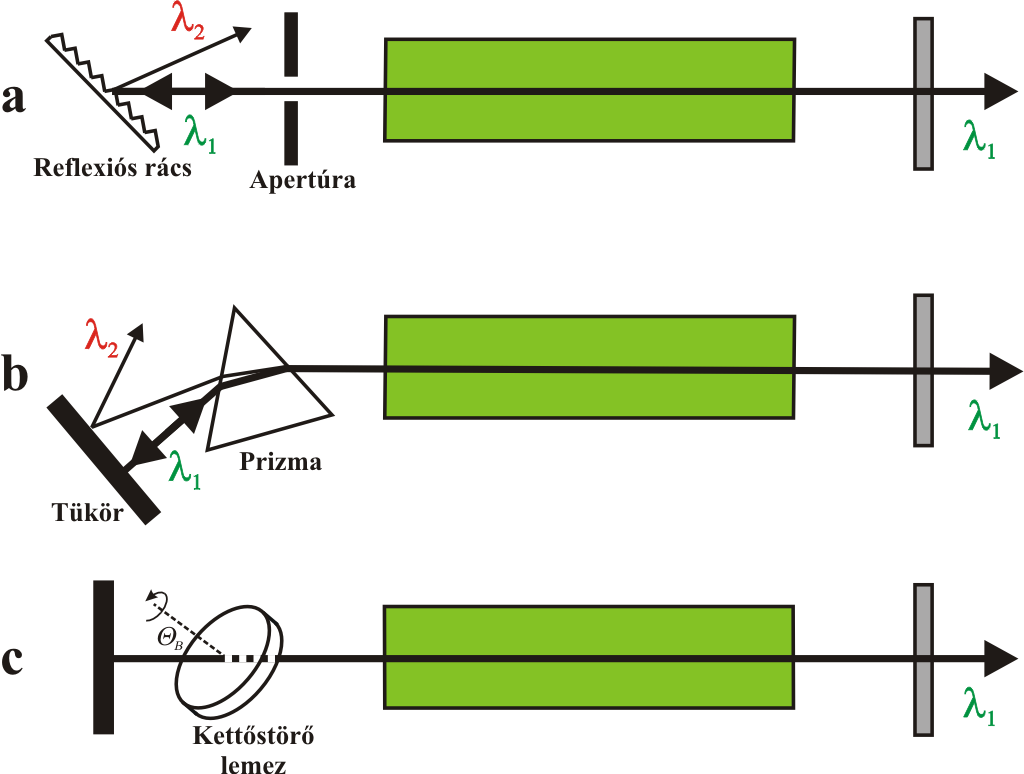
6.7. ábra. Lézerek hangolására alkalmas elrendezések.
Látható és közeli infravörös tartományon egy diszperziós prizmát építenek be az aktív közeg és a hátoldali tükör közzé (6.7.b ábra) és a prizma forgatásával lehet szabályozni, hogy a tükör milyen hullámhosszú fényt tükrözzön vissza ugyanazon az optikai úton.
Ugyancsak a látható és közeli infravörös tartományban alkalmazzák a kettőstörő lemezt (6.7.c ábra). A működési elve a következő. Vegyünk két, egymással párhuzamosan állított polarizátort és helyezzünk el egy kettőstörő lemezt úgy, hogy Brewster szöget zárjon be a beeső nyalábbal, a beesési sík pedig egybeessen a polarizációs síkkal a reflexiós veszteség kiküszöbölése érdekében. Ha kettőstörő optikai tengelye (mely párhuzamos a lemez síkjával) nem párhuzamos a beesési síkkal és nem is merőleges rá, akkor a térerősség vektornak lesz egy ordináruis és egy extraordinárius komponense, melyek a lemezen való áthaladás következtében ΔΦ fáziskülönbséggel rendelkeznek:
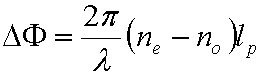 |
, | (6.44) |
ahol lp a kettőstörőben megtett távolság. Ha ΔΦ a 2π egész számú többszöröse, akkor a kettőstörőből kilépő nyaláb lineárisan polarizált marad, ellenkező esetben elliptikusan polárossá válik. Az elliptikusan polarizált fény a polarizátoron áthaladva energiát veszít. Ha az így hullámhosszfüggő rezonátorveszteség meghaladja a közeg erősítését, akkor az adott hullámhossz nem tud erősödni. A működési hullámhossz hangolását a kristálynak a felület normálisa körüli forgatásával lehet megvalósítani, amely megváltoztatja a kristály optikai tengelye és a térerősség-vektor közötti szöget és ezáltal az ne értékét. A (6.44) egyenletből kiszámítható, hogy a szűrő két szomszédos maximuma közötti különbség (szabad spektrális tartomány)
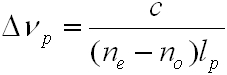 |
, | (6.45) |
azaz minél vékonyabb a lemez, annál nagyobb a hangolható tartomány, ami a feloldóképesség csökkenését eredményezi.
Kis erősítéssel rendelkező lézerek esetén nincs feltétlenül szükség külön polarizáló elemekre, hiszen a lézerközeg határfelületének Brewster beesési szögű kialakítása már biztosítja a polarizált lézerműködést, ugyanakkor a kettőstörő lemeznek a szintén Brewster szögű kialakítása miatti részlegesen polarizáló tulajdonsága kilépéskor elegendő csillapítást okozhat az elliptikusan polarizált módusban.
A lézerrezonátorokban azon frekvenciájú hullámok tudnak erősödni, melyek állóhullámot tudnak létrehozni. Állóhullámok kialakulásának feltétele, hogy egy teljes körbefutás alatt a fázisváltozás
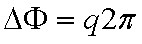 |
, | (6.46) |
ahol q egész szám. A fenti feltételt teljesítő hullámok (módusok) közötti frekvenciakülönbség jóval kisebb, mint a lézerátmenetek vonalalakjának szélessége, ezért a többmódusú oszcilláció a lézerek általános jellemzője. Kiszámítható (4.21 egyenletből), hogy a lézerekre leggyakrabban jellemző TEM00 transzverzális Gauss alapmódusok frekvenciája
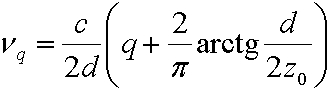 |
, | (6.47) |
ahol d a rezonátor optikai úthossza, z0 pedig a nyaláb Rayleigh hossza. Ezen longitudinális módusok közötti
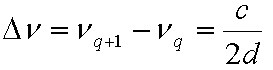 |
(6.48) |
frekvenciakülönbség megegyezik a síkpárhuzamos rezonátorok esetén síkhullámokra kapható értékkel, annak ellenére, hogy a fázisterjedés és a sajátfrekvenciák értéke eltérő a két hullámtípus esetén. Ha a magasabb rendű TEM mp módusokat is figyelembe vesszük, a spektrum még összetettebb lesz. Az adott longitudinális módushoz tartozó transzverzális módusok frekvenciája eltolódik, ezek fedésbe kerülhetnek más longitudinális alapmódusokkal.
A többmódusú oszcilláció leírásához az egyszerűség kedvéért vegyük figyelembe csak a TEM00 alapmódusokat és feltételezzük, hogy az egyik sajátfrekvencia egybeesik a vonalalak csúcsával A lejátszódó folyamatokat nagymértékben befolyásolja a vonalalak kiszélesedésének természete.
Vizsgáljuk meg, mi történik, ha egy (kristályhibák és Doppler eltolódás okozta) inhomogén kiszélesedésű lézerátmenetünk van. A kiszélesedést okozó folyamatok természete miatt a vonalalak a különálló atomok (pl. sebességfüggő) vonalalakjának szuperpozíciójából épülnek fel, ezért az abszorpciós vagy emissziós spektrumba telítődéssel lyukat lehet "égetni". Az előzőekben láttuk, hogy a lézerműködés akkor indul be, amikor elérjük a kritikus populációinverziót (Rcp pumpálási sebességnél), ami elég nagy erősítést biztosít a rezonátor veszteségeinek kompenzálásához. Amikor a központi módus "beindul" annak ellenére, hogy a pumpálási sebességet tovább növeljük, az adott frekvenciához tartozó populációinverzió állandó értéken marad lyukat égetve az erősítési görbébe (6.8. ábra).
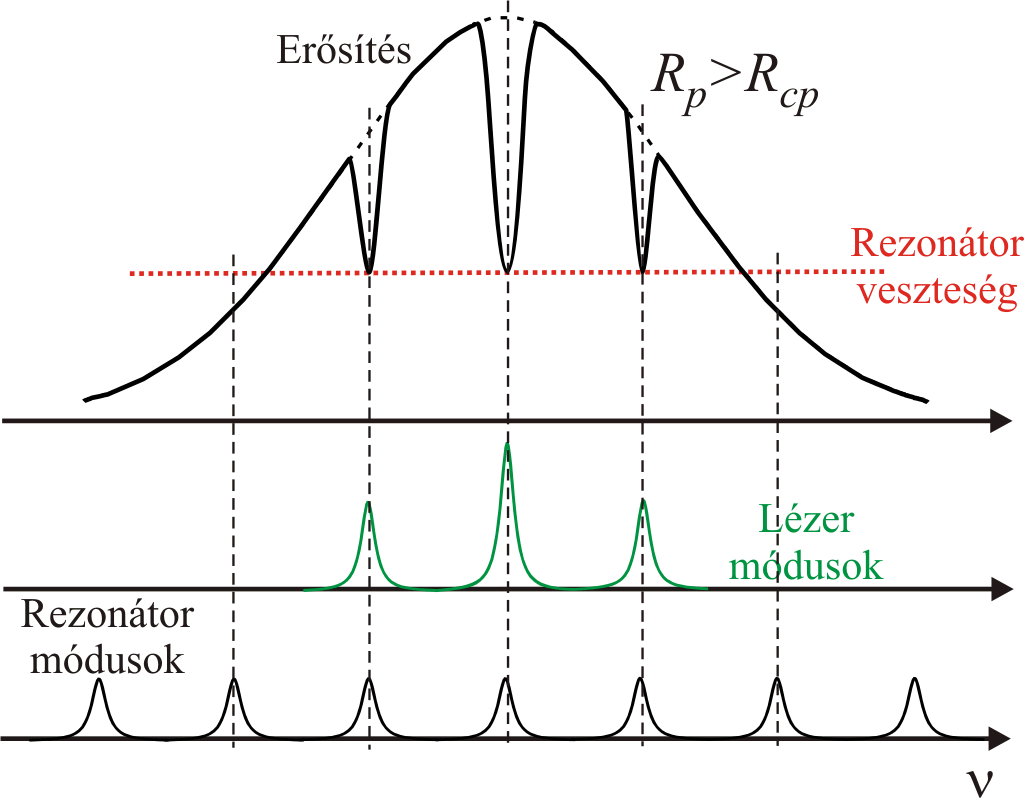
6.8. ábra. Többmódusú lézerműködés kialakulása inhomogén kiszélesedésű lézerátmenet esetén.
A pumpálás növelésével egyre több módus erősítése éri el a kritikus értéket melyek szintén lyukat égetnek az erősítési görbébe (a két haladási iránynak megfelelően a csúcstól számított mindkét oldalon). Röviden összegezve, inhomogén kiszélesedésnél a különböző módusok nincsenek hatással egymás működésére, a lézerműködés feltétele a kritikus erősítés elérése.
Homogén kiszélesedés esetén az erősítési görbe alakja változatlan marad, függetlenül attól, hogy a lézerműködés milyen frekvencián megy. Amint a 6.9. ábra szemlélteti, az erősítési görbe csak addig emelkedik, amíg eléri a rezonátor veszteség értékét és a középponti módusban beindul a lézerműködés. Mivel a többi, oldalsó módusnak kisebb az erősítése, ezek nem tudnak feléledni.
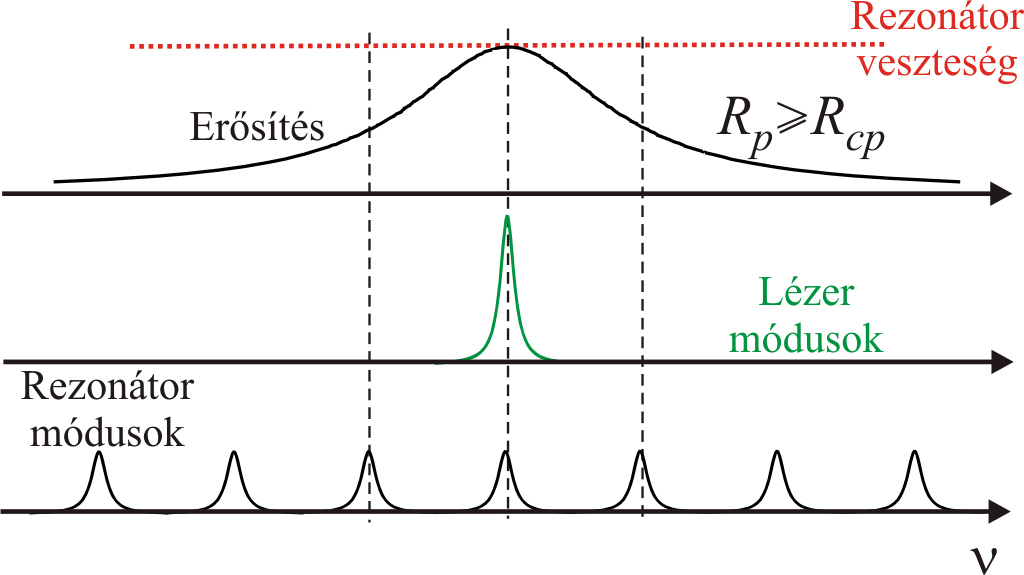
6.9. ábra Egymódusú működés homogén kiszélesedésű lézerátmenet esetén.
A gyakorlatban viszont megfigyeltek többmódusú működést homogén kiszélesedett átmenetek esetén is. Lézermodellünkben feltételeztük, hogy a populációinverzió azonos az aktív közeg teljes térfogatában és nem vettük figyelembe azt, hogy az egyes módusok állóhullámot hoznak létre, ami azt jelenti hogy a csomópontokban a térerősség kicsi és nem lesz indukált emisszió. Emiatt ezeken a helyeken a populáció inverzió magas lesz, a rezonátorban térben λ/2 térbeli periódussal rendelkező lesz a populációinverzió értéke (térbeli "lyuk égetés"). Két szomszédos módus között a rezonátor középső szakaszán λ/4 lesz az eltolódás, ez pedig lehetőséget adhat egy második módus kialakulására.
Az erősítési görbének és a lézermódusok kialakulásának az Rp pumpálási sebességtől való függését mind inhomogén, mind pedig homogén vonalkiszélesedés esetén a 6.10. ábrán látható animáció szemlélteteti:
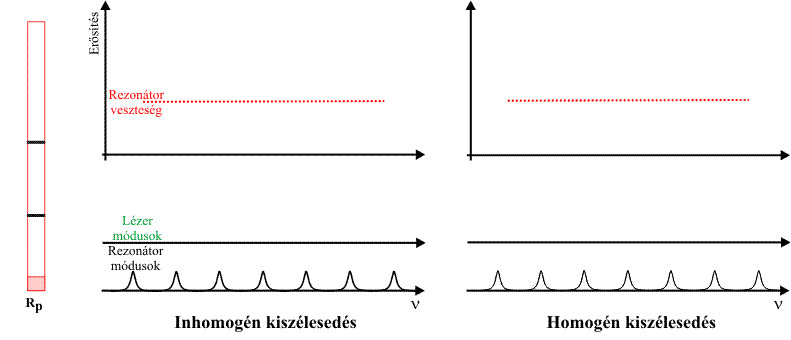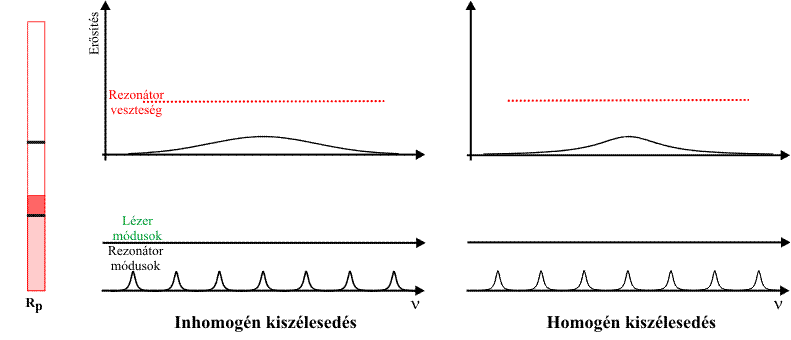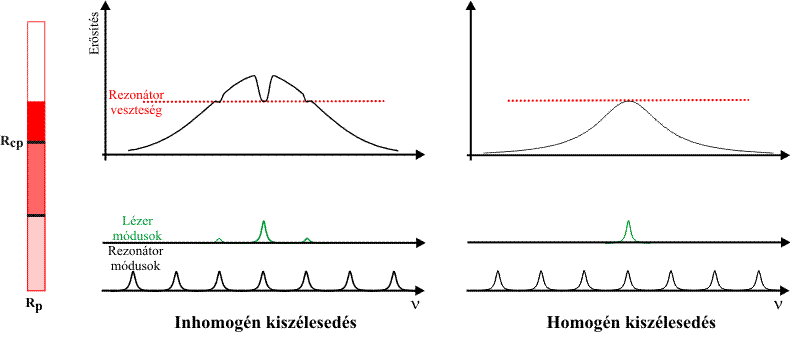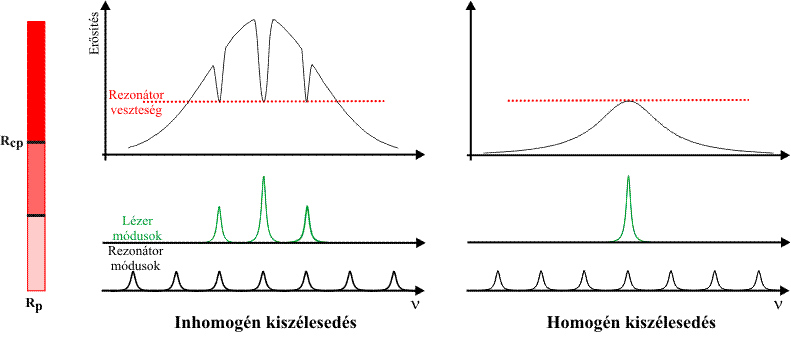
6.10. ábra. A lézermódusok függése az az Rp pumpálási sebességtől.
Kis nyalábátmérővel rendelkező lézerek esetén (pl. < 0,5 mm átmérőjű HeNe, vagy < 1 cm átmérőjű CO2 lézer) a kívánt transzverzális módusban való lézerműködés megvalósítása egyszerű. A 4. fejezetben láthattunk, hogy a különböző transzverzális módusok intenzitáseloszlása nagymértékben különbözik egymástól. Megfelelő alakú apertúrának a rezonátorba helyezésével elérhetjük, hogy csak a kívánt módus tudjon erősödni. A leginkább favorizált a TEM00 alapmódusú lézerműködéshez egy megfelelő méretű kör alakú apertúrát alkalmaznak, mely a magasabb rendű módusok esetén nagyobb veszteséget okoz, mint a lézerközeg erősítése, miközben az alapmódus vesztesége alacsony maradhat.
Nagy nyalábátmérők esetén (a Fresnel szám nagyobb, mint 2) az apertúrázás a fellépő instabilitások miatt nem megoldható. Instabil rezonátorok alkalmazásával elérhető az alapmódusú működés, az ilyen lézer intenzitásprofilja viszont gyűrűszerű, középen csökkent intenzitással. Ez a hiányosság viszont kiküszöbölhető radiálisan változó transzmissziós profillal (Gauss, vagy szuper-Gauss) rendelkező kicsatoló tükör alkalmazásával.
Az egyetlen transzverzális módussal rendelkező lézerben még mindig lehetséges több longitudinális módus működése. Láttuk, hogy a módusok közötti frekvenciakülönbség fordítottan arányos a rezonátor optikai úthosszával. Bizonyos esetekben járható út lehet, hogy a rezonátor méretét úgy válasszuk meg, hogy az egyik módus egybeessen az erősítési görbe csúcsával, a két szomszédos módus frekvenciája a görbe széleire essen, ahol az erősítés kisebb lesz, mint a rezonátor vesztesége. 632,8 nm-en működő He-Ne lézer estén az erősítési görbe félérték-szélessége ~ 1,7 GHz, ami azt jelenti, hogy ~ 15 cm rezonátor hosszal elérhető az egymódusú működés. Széles erősítési görbével rendelkező aktív közegek esetén (pl. festéklézerek) a feltételeknek megfelelő túl kicsi rezonátorméret miatt nem járható út. Bizonyos esetekben a nagy teljesítmény, vagy alacsony erősítés miatt hosszú rezonátorokra van szükség, melyekkel úgyszintén nem teljesíthető az egymódusú működés feltétele.
Egyetlen longitudinális működési módus kiválasztására alkalmas eszköz a rezonátorba elhelyezett Fabry-Perot etalon. Az etalon legegyszerűbb változata egy síkpárhuzamos lemez, melynek mindkét felületét nagy reflexiójú bevonattal látták el. Az etalont úgy helyezik a rezonátorba, hogy a felületének normálisa a lézernyalábbal valamilyen kis szöget zárjon be, így nem hozhat létre másodlagos rezonátort a rezonátoron belül (6.11. ábra).

6.11. ábra. Fabry-Perot etalon elhelyezkedése a rezonátorban longitudinális módusszelekcióhoz.
Az eltalonból többszörös visszaverődés után kilépő nyalábok közötti interferencia maximum-feltételéből kiszámítható a transzmissziós maximumok közötti frekvenciakülönbség, vagy szabad spektrális tartomány
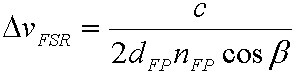 |
, | (6.49) |
ahol n FP és dFP az etalon anyagának törésmutatója, illetve vastagsága, β pedig a fény törési szöge. Az etalon a beesési (törési) szög kismértékű forgatásával hangolható, hogy valamelyik transzmissziós maximuma az erősítési görbe közepe közelébe essen (6.11. ábra). Az etalon vastagságát úgy kell megválasztani, hogy ΔνFSR nagyobb legyen, mint az erősítési görbe Δν0 félérték-szélességének a fele, azaz
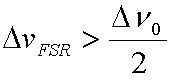 |
. | (6.50) |
Ahhoz, hogy csak egyetlen módus erősödjön, a FP etalon transzmissziós csúcsának ΔνFP félérték-szélessége kisebb kell legyen, mint a rezonátor módusai közötti frekvenciakülönbség kétszerese, azaz:
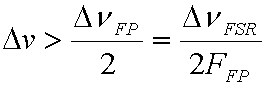 |
, | (6.51) |
ahol FFP az etalon finesse -e, amelyet a ΔνFP/ΔνFSR arányként definiálnak. A finesse szoros összefüggésben van az etalon reflexiójával. A nagy finesse, azaz a jó spektrális felbontás nagy reflexiós tényezőt (kicsi transzmissziót) feltételez, ami miatt nagy lesz a rezonátor vesztesége. Emellett a finesse növelésének technológiai korlátai vannak. Emiatt előfordulhat (nagy rezonátor hossz és széles erősítési görbe esetén), hogy az egymódusú működést csak két (egy vékony és egy vastag) etalon egyidejű alkalmazásával lehet elérni.
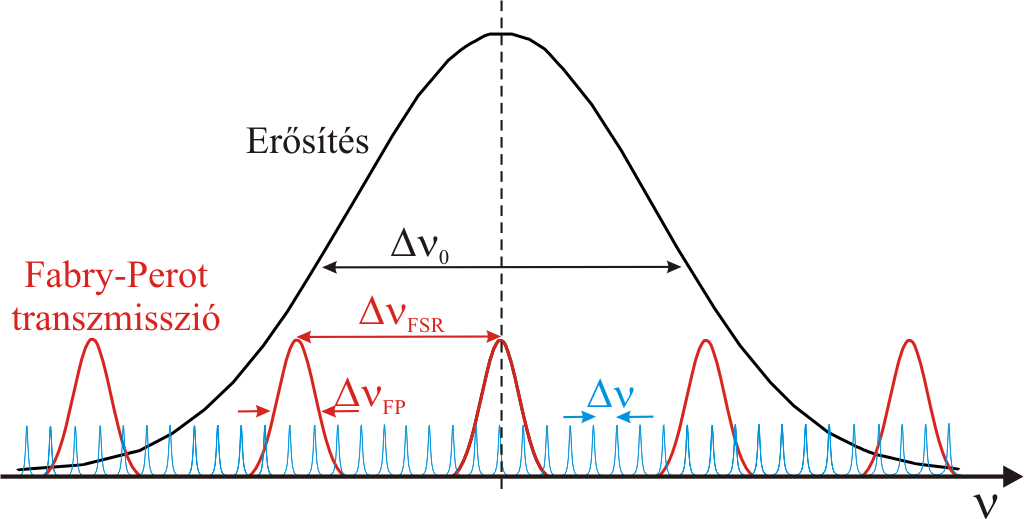
6.12. ábra. Egymódusú lézerműködés megvalósításának elve Fabry-Perot etalon alkalmazásával.
Homogén, de nem túl nagy kiszélesedésű átmeneten alapuló, gyűrűrezonátort alkalmazó lézerek esetén, amennyiben egyirányú a lézerműködés, az egy longitudinális módusú oszcilláció önmagától is megvalósul. Ennek oka, hogy az ilyen lézerekben nem jön létre állóhullám interferencia, így a (több módus kialakulását okozó) térbeli "lyuk égetés" sem alakulhat ki.
A rezonátor saját módusainak Δνc sávszélességét a rezonátor τc fotonélettartama határozza meg. Minél nagyobb a tükrök reflexiója, a fotonok annál több kört tesznek meg a rezonátorban, ami ahhoz vezet, hogy a rezonanciafeltétel maximumától távolabb eső hullámok annál jobban kioltódnak, ami a sávszélesség csökkenéséhez vezet:
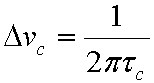 |
. | (6.52) |
Ha sikerül tetszőlegesen hosszú rezonátor élettartamot létrehozni, akkor elvileg akármilyen keskeny sávszélességet elő tudunk állítani. Felmerül a kérdés, hogy mégis mi lehet a monokromatikusság korlátja. A kérdést még a lézerek megépítése előtt megválaszolták. Akármilyen tökéletes is lehet egy rezonátor, a spontán emisszió okozta kvantum-zaj fluktuáció mindig létrehoz egy minimális vonalszélességet, melynek értékét a Schawlow-Townes formula adja meg:
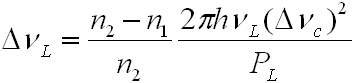 |
. | (6.53) |
Ez a kvantumzaj korlát nagymértékben függ a lézer típusától. Míg egy He-Ne lézer esetén mHz körüli alacsony érték is lehet, addig egy félvezető lézerben (a ps-os) élettartam miatt a MHz-et is elérheti. A rezonátor állóhullám-feltételéből kiindulva levezethető, hogy a rezonátor optikai úthosszában bekövetkező relatív változás megegyezik a működési frekvenciában vagy hullámhosszban bekövetkező relatív változással. Így könnyen belátható, hogy lehetetlenség például olyan rezonátort építeni, melynek stabilitása megfelelne a He-Ne lézerre elméletileg elérhető ΔνL/νL relatív sávszélesség ~10-18 nagyságrendjének. A lézerek sávszélességének alsó határát a gyakorlatban a rezgések, hőmérséklet-, vagy akár nyomásváltozások okozzák, melyek mind befolyásolják a rezonátorban megtett optikai úthosszat.
A hullámhosszváltozásokat az őket létrehozó folyamatok időbeli lefolyása szerint két csoportba oszthatjuk: hosszútávú (>> 1s) drift és gyors fluktuációk. A lassú frekvencia-eltolódás okai főleg a környezeti hőmérséklet- és nyomásváltozás. Amennyiben szükséges (pl. spektroszkópiai alkalmazásoknál) ezek hatása kiküszöbölhető alacsony hőtágulási együtthatójú anyagok (~10-7 1/ºC) felhasználásával, a környezeti hőmérséklet állandó értéken tartásával és nyomásstabilizált rezonátorok alkalmazásával. Ezekkel a módszerekkel MHz-es hosszú távú stabilitást lehet elérni. A rövid távú fluktuációkat rezgések, akusztikus hullámok (lokális nyomás- és törésmutató változás), a gerjesztési teljesítmény egyenetlenségei (hőmérsékletváltozás az aktív közegben), stb. okozzák. A fluktuációk okozta frekvenciaingadozást passzív módszerekkel ~MHz alá csökkenteni nagyon nehéz. Különleges hullámhossz-stabilitási igények esetén (pl gravitációs hullám detektor) a rezonátor egyik tükrét piezolelektromos eltolókra helyezik, melyeket nagy pontosságú frekvencia-diszkriminátorok által adott visszacsatolási jellel vezérelnek. Frekvencia-diszkriminátorként nagy hosszúságú (akár 1m!) Fabry-Perot interferométert vagy nagyon keskeny abszorpciós vonallal rendelkező gázcellát lehet alkalmazni, melyekkel akár néhány kHz-es frekvencia-stabilitást is el lehet érni.
Hasonlítsa össze a három- és négyszintes termsémájú lézerek viselkedését a pumpálási sebesség függvényében. Magyarázza meg az eltérések és hasonlóságok okait.
Hogyan befolyásolja a lézerek működését az energiaszintek közötti átmenet kiszélesedésének típusa?
-
Adott egy 1 m hosszúságú rezonátorunk, melyben a lézerközeg inhomogén kiszélesedésű lézerátmenetének sávszélessége Δν0 = 10 GHz. Feltételezzük, hogy a lézer polarizált fényt bocsát ki.
a) Milyen paraméterekkel (vastagság, finesse) rendelkező Fabry-Perot etalont kell ebben a rezonátorban elhelyezni az egymódusú lézerműködéshez? Az etalon törésmutatója 1,5, a dőlésszöge pedig β = 3º-nak megfelelő.
b) Ha az etalon finesse-e nem lehet nagyobb, mint 30, milyen paraméterekkel kell rendelkezzen az egymódusú működéshez szükséges második FP etalon?
-
Adott egy 50 cm rezonátor hosszúságú lézer, melyben az 1,5 törésmutatójú aktív közeg (szilárd) a teljes hossz 80%-át teszi ki. Az elvárt relatív hullámhossz stabilitás 10-6.
a) Feltételezve, hogy a rezonátorban a légnyomás megegyezik a környezetével, mekkora lehet a maximális légköri nyomás változás a megfelelő stabilitás megőrzéséhez?
b) Ha a rezonátor egyik tükrét piezoelektromos eltolóhoz rögzítik, mi az összefüggés az eltoló elmozdulása és a légköri nyomásváltozás között stabil lézerműködés esetén?
[6.1] A.E Siegman: Lasers (University Science Books, 1986)
[6.2] J.T. Verdeyen: Laser Electronics (3ed. Prentice hall, 1995)
[6.3] O. Svelto: Principles of lasers (4ed., Springer, 1998)
[6.4] Open Access Encyclopedia for Photonics and Laser Technology (RP Photonics GmbH) http://www.rp-photonics.com/encyclopedia.html
Tartalom
Ebben a fejezetben megvizsgáljuk, hogy hogyan működik a lézer akkor, amikor a gerjesztés és/vagy a rezonátorveszteség időfüggő [7.1]. Ezen esetekben tranziens lézerműködésről beszélünk. A tranziens működés két típusra bontható attól függően, hogy egymódusú vagy többmódusú lézerműködésről van szó. Amikor a lézer egy longitudinális módusban üzemel, akkor a korábban megismert sebességegyenletekkel jól leírható a működése. Ehhez az esethez tartozik a relaxációs oszcilláció, a Q-kapcsolás, az erősítés-kapcsolás és a rezonátor kiürítés (cavity-dumping). A másik eset, amikor több longitudinális módus is egyidejűleg jelen van a rezonátorban, pl. módusszinkronizáció esetében, ekkor más leírási módot kell használnunk. Az egyik az ún, frekvenciaképbeli leírás, amikor külön-külön vizsgáljuk a különböző frekvenciájú módusok működését, és ezek összege adja meg a kialakuló lézerteret. A másik leírási mód az ún. időképbeli leírási mód, amikor úgy tekintjük az impulzusüzemű lézert, hogy egy impulzus halad körbe-körbe a rezonátorban.
Először tekintsük azt az esetet, amikor a pumpálási sebesség időfüggése egy lépcsőfüggvénnyel írható le, azaz Rp = 0, ha t < 0, majd t>0 esetében Rp = állandó értékű. Továbbá feltételezzük, hogy a lézer egy módusban üzemel. Ekkor a 6. fejezetben ismertetett sebességegyenletek alkalmazhatók a lézer működésének leírására. Az egyenletek analitikus megoldása szempontjából problémát jelent, hogy a q fotonszám és a Δn populáció inverzió szorzata szerepel bennük, az nemlineárisak a q és a Δn változókat illetően. Ezért általános esetben az egyenletek csak numerikusan oldhatók meg.
A rubin lézer esetében elsőként végezték el az egyenletek numerikus megoldását, melynek eredményét mutatja a 7.1 ábra [7.2]. Kezdeti feltételként legyen a teljes populáció ( nt ) az alsó nívón, azaz Δn = -nt. A rezonátorbeli fotonszám legyen kicsi egészszám, pl. 1, amely már lehetővé teszi, hogy a lézerműködés beinduljon. A 7.1 ábrán látható lézerműködéshez hasonló eredményeket várunk a négyszintes lézerekre is, csak ott a kezdeti feltétel Δn = 0. Ha a 7.1 ábrán a kezdő időpontot eltoljuk a 2 μs-hoz, ahol a populáció inverzió eléri a 0 értéket, akkor a négyszintes lézer működése is az ábra segítségével kvalitatívan tárgyalható.
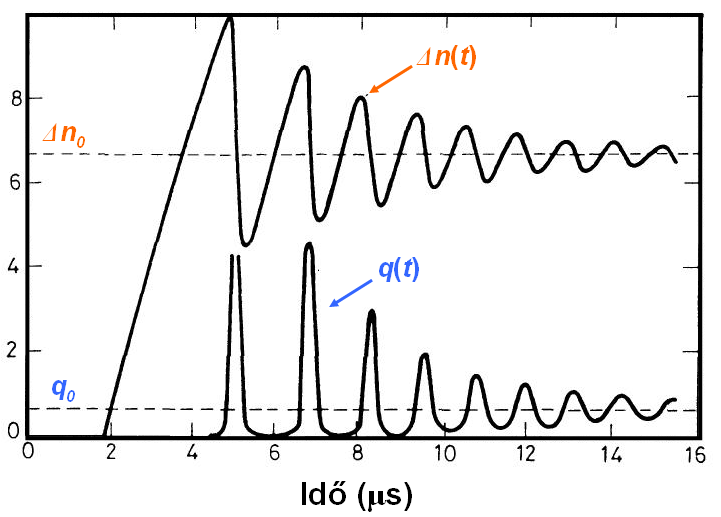
7.1. ábra. A populációinverzió (Δn) és a fotonszám (q) változása az idő függvényében rubin lézer esetét modellezve [7.2].
2 μs-nál a populációinverzió már meredeken nő a pumpálás miatt, azonban a fotonszám még mindig igen alacsony értékű, közel a kezdeti értékhez. 3,5 μs-nál lépi át a populációinverzió a Δn0 küszöbértéket, ami azt eredményezi, hogy ekkor már a fotonszám is elkezd nőni. Amikor a fotonszám elég naggyá válik, akkor az indukált emisszió a domináns a pumpálással szemben. A populációinverzió ezért elkezd csökkeni, és a küszöbértékre akkor esik le, amikor a fotonszám a maximumát éri el, azaz dq/dt = 0. Ezen időpont után is a Δn tovább csökken, mert a fotonszám továbbra is nagyon magas. Csakhogy ekkor a lézer már az erősítési küszöb alatt van, így a fotonszám meredeken esni kezd. Amikor a fotonszám olyan kicsi lesz, hogy ismét a pumpálás válik dominánánsá, akkor újra elkezd nőni a populációinverzió értéke. Ez a folyamat így periódikusan ismétlődik, ami azt eredményezi, hogy a fotonszám időfüggése csúcsok sorozatából (laser spikes) áll csökkenő amplitúdóval, és az egymást követő csúcsok között nagyjából azonos idő telik el. Így a lézer kimenő teljesítménye is hasonló időbeli változást mutat. Ezt a jelenséget hívjuk relaxációs oszcillációnak. Vegyük észre, hogy nemcsak a fotonszám oszcillál időben, hanem a populációinverzió is, mely megelőzi egy fél periódussal a fotonszám hullámzását. Látható, hogy relaxációs oszcilláció lecsengésével végül kialakul egy állandósult lézerműködés.
A fenti jelenség leírására próbáljunk meg analitikus megoldást is találni. Ehhez tekintsünk egy négyszintes lézert, melynek a működését az alábbi sebességegyenletek írják le:
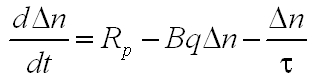 |
. | (7.1) |
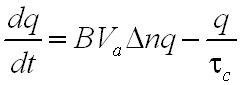 |
. | (7.2) |
A fenti egyenletek a (6.9) és (6.11) egyenleteknek felelnek meg, csak a szemléletesebb q fotonszámot használtuk a I fotonszámintenzitás és a σ hatáskeresztmetszet szorzata helyett. Va az erősítő közeg térfogatát jelöli. Végezzük el a kisjelű perturbációs analízist a fenti egyenleteken, azaz az állandósult állapot Δn0 és q0 értékéhez képest kicsit változzon a Δn populáció inverzió és a q fotonszám:
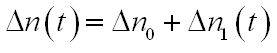 |
, | (7.3) |
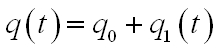 |
(7.4) |
ahol az 1-es indexű mennyiségek nagyon kicsinyek az állandósult értékekhez képest. A (7.3) és (7.4) egyenleteket (7.1)-be illetve (7.2)-be helyettesítve kapjuk, hogy
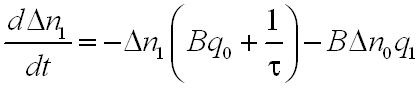 |
, | (7.5) |
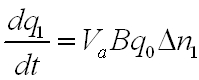 |
. | (7.6) |
Itt kihasználtuk, hogy állandósult állapotban, azaz dq0/dt = 0 esetén (7.2)-ből
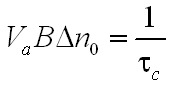 |
. | (7.7) |
Ezután deriváljuk (7.6)-ot idő szerint, majd helyettesítsük be (7.5)-öt:
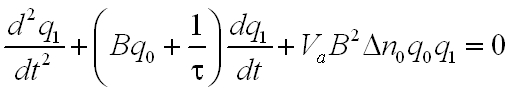 |
. | (7.8) |
A (7.8) egyenlet megoldását keressük az alábbi alakban:
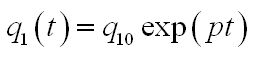 |
. | (7.9) |
A p paraméterre a
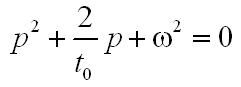 |
(7.10) |
másodfokú egyenletet kapjuk, ha (7.9)-et behelyettesítjük (7.8)-ba, és bevezetjük a t0 és ω mennyiségeket a következő definíciókkal:
 |
(7.11) |
és
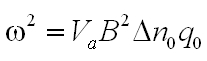 |
. | (7.12) |
A (7.10) egyenlet megoldása:
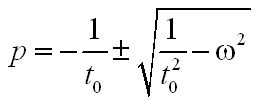 |
. | (7.13) |
Először tekintsük azt az esetet, amikor 1/t0 < ω. Ekkor p komplex szám lesz, azaz
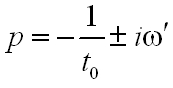 |
, | (7.14) |
ahol
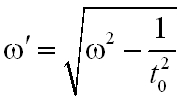 |
. | (7.15) |
Láthatjuk, hogy a (7.8) egyenlet megoldása ebben az esetben egy csillapodó rezgés:
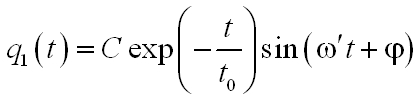 |
, | (7.16) |
ahol a C és φ együtthatókat a kezdőfeltételekből határozhatjuk meg.
A Δn1 populációinverzió időfüggését is megkaphatjuk, ha (7.16)-ot (7.6)-ba helyettesítjük, és feltételezzük, hogy 1/t0<<ω'
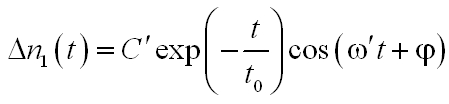 |
. | (7.17) |
Láthatjuk, hogy Δn1 is az idő függvényében egy csillapodó rezgést ad, de egy fél oszcillációs periódussal el van tolódva, mivel először az inverziónak kell megnövekedni és utána a fotonszámnak, összhangban a 7.1. ábrával.
Érdemes bevezetni a relatív pumpálási sebességet:
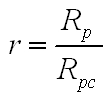 |
, | (7.18) |
ahol az Rpc kritikus pumpálási sebességet megadó (6.14) kifejezést átírva a fentiekben is használt jelölésekre:
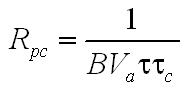 |
. | (7.19) |
Ekkor a t0 csillapodási idő illetve a rezgés ω körfrekvenciája kifejezhető úgy, mint
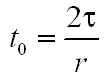 |
(7.20) |
és
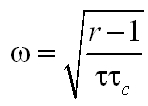 |
. | (7.21) |
Példaként vizsgáljuk meg egy gyűrűrezonátorú Nd:YAG lézerben (7.2. ábra) kialakuló csillapodó rezgés jellemzőit, ahol a fénysugárnak a rezonátorbeli útja nem egy síkban van. Tételezzük fel, hogy a fent alkalmazott modellünk alkalmazható erre a lézerre. A relatív pumpálási sebesség legyen r = 5. Mivel a felső nívó élettartama τ = 230 μs, így (7.20)-ból t0 = 92 μs adódik. A rezonátor paraméterei alapján a rezonátor átlagos fotonélettartama τc = 7,8 ns, így (7.21)-ből a relaxációs oszcilláció frekvenciájára 238 kHz-et kapunk. Ezt az értéket összevetve a t0-ra kapott értékkel, teljesül a t0 >> 1/ω feltétel, azaz valóban ω' ≈ ω.
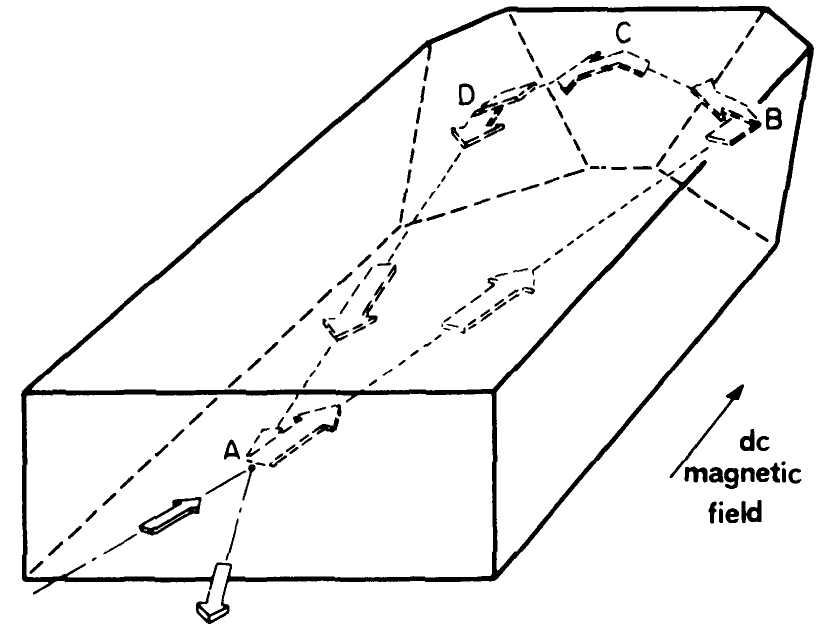
7.2. ábra. Egy longitudinális módusban működő Nd:YAG lézer, melynek a gyűrű alakú rezonátorában a fény egy irányban, de nem egy síkban halad körbe [7.3.].
Tudjuk, hogy egy csillapodó rezgésnek a spektruma Lorentz-görbe alakú, melynek a félértékszélessége Δν = 1/2πt0 = 1,73 kHz. A 7.3 ábra mutatja a példában vizsgált Nd:YAG lézer zajspektrumát. Látható, hogy zajcsökkentés nélkül valóban van egy csillapodó relaxációs oszcilláció a kimenő lézernyaláb teljesítményében, amire a Lorentz-görbe alak utal. A rezgés frekvenciája is közel annál az értéknél van, amit kiszámoltunk az előbb.
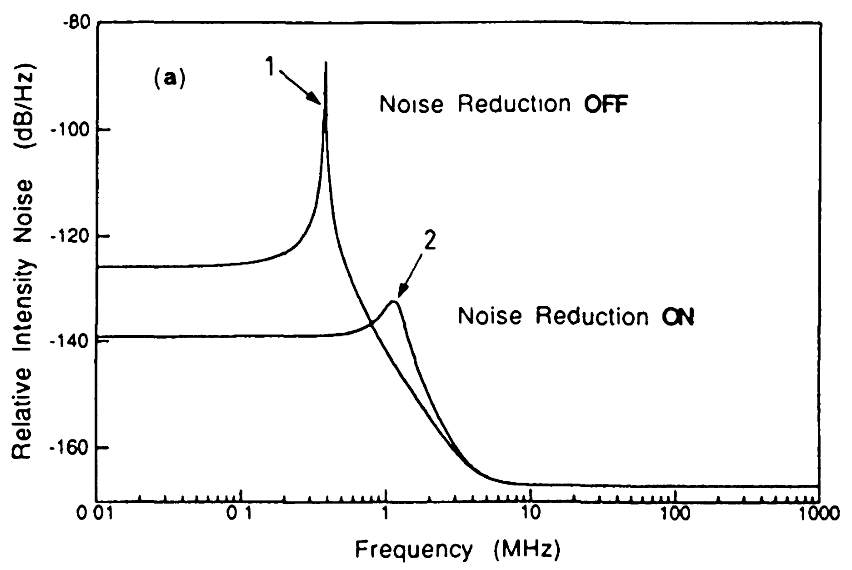
7.3. ábra. Tipikus relatív intenzitás zajspektruma egy diódapumpált Nd:YAG lézernek, melynek a rezonátora a 7.2 ábrán látható. Az 1-es görbénél nincs, míg a 2-es görbénél be van kapcsolva a zajcsökkentés [7.1.].
Ha a t0>1/ω feltétel nem teljesül, akkor a (7.13) egyenlet megoldása p-re két valós, negatív számot ad. Ebben az esetben q1(t) időbeli viselkedése a két exponenciálisan csökkenő görbe szuperpozíciójaként áll elő. A t0<1/ω feltétel teljesüléséhez (7.20) és (7.21) alapján kapjuk, hogy
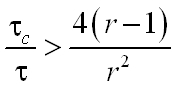 |
. | (7.22) |
Mivel az egyenlőtlenség jobb oldalán lévő kifejezés r = 2-nél veszi fel a maximális értékét, ami 1, így ha τc > τ, akkor bármely r relatív pumpálási sebesség értékre teljesül a fenti feltétel. Ez a helyzet gyakran fennáll gázlézerekre, ebből következően e lézertípusnál nem jellemző a fejezetben említett tranziens viselkedés. Például egy He-Ne lézer esetében a 632,8 nm hullámhosszú vonalhoz tartozó átmenetnél τ = 50 ns, míg τc = 322 ns. Ha r = 1,5, akkor (7.20) és (7.21)-ből t0 = 66,6 ns és ω = 5,6 MHz adódik. A két relaxációs idő (7.13) alapján 1 μs és 33,3 ns.
A fejezetben tárgyalt egyszerűsített modell sok esetben nem írja le jól egy adott lézer működése során bekövetkező oszcillációkat. Előfordul, hogy az intenzitáscsúcsok szabályosan, más esetekben viszont szabálytalanul jelennek meg. A 7.4. ábrán látható, hogy egy folytonosan gerjesztett rubin lézer kimenő fénye impulzussorozatból áll. Mind az impulzusok közötti idő, mind az impulzusok amplitúdója véletlenszerűen változik. Továbbá nem alakul ki az állandósult állapot, hanem fokozatosan csökken a jel átlagértéke.

7.4. ábra. Egy korai fejlesztésű folytonosan pumpált szilárdtest lézer fényének tipikus időbeli viselkedése [7.4]. Az időskála 50 μs/osztás.
Az egymódusú lézereknél a lézerfény zajának fő oka főként a pumpálás illetve a rezonátorveszteség időbeli változása. Ha például egy szinuszos moduláció van a lézer pumpálásában, akkor a lézer kimenő teljesítménye is a moduláció frekvenciája szerint változik. Ez a hatás különösen erős, ha a moduláció frekvenciája megegyezik a moduláció nélkül létrejövő relaxációs oszcilláció frekvenciájával. De ezen kívül más, belső oka is lehet az instabilitásnak, ami oszcillációhoz vagy akár kaotikus működéshez is vezethet. A multimódusú lézerek esetében a módusok közötti időleges kapcsolódás is eredményez instabil működést.
Az előbbi részben láttuk, hogy a populációinverzió csak kismértékben lépi túl a lézerműködéshez szükséges küszöbértéket, mivel az indukált emisszió beindulása csökkenteni kezdi a populációinverziót. Ha azonban a rezonátorban elhelyezünk egy kapcsolót, ami a lézerműködést megakadályozza, akkor a pumpálás hatására a populációinverzió a küszöbértéket jóval nagyobb mértékben meghaladhatja (7.5. ábra). Ha hirtelen kinyitjuk a kapcsolót, akkor az erősítés jóval nagyobb a veszteségnél, és a beinduló lézerműködés hatására a rezonátorban tárolt nagy mennyiségű energia egy rövid időtartamú, nagy intenzitású impulzus formájában lép ki a rezonátorból. Mivel ez a technika a rezonátor Q jósági tényezőjének ((1.53) egyenletet) egy alacsony értékről magas értékre történő kapcsolására épül, ezért ezt a technikát röviden Q-kapcsolásnak nevezzük. A kibocsátott impulzus időtartama összemérhető a rezonátor átlagos fotonélettartamával, azaz az impulzus időbeli hossza néhány nanoszekundum és néhányszor tíz nanoszekumdum közé esik, és a teljesítménye MW-os tartományban van. Így a Q-kapcsolt impulzus csúcsteljesítménye 3-4-szerese lehet a hosszú impulzusú üzemmód helyett ugyanakkora pumpálási sebesség mellett.
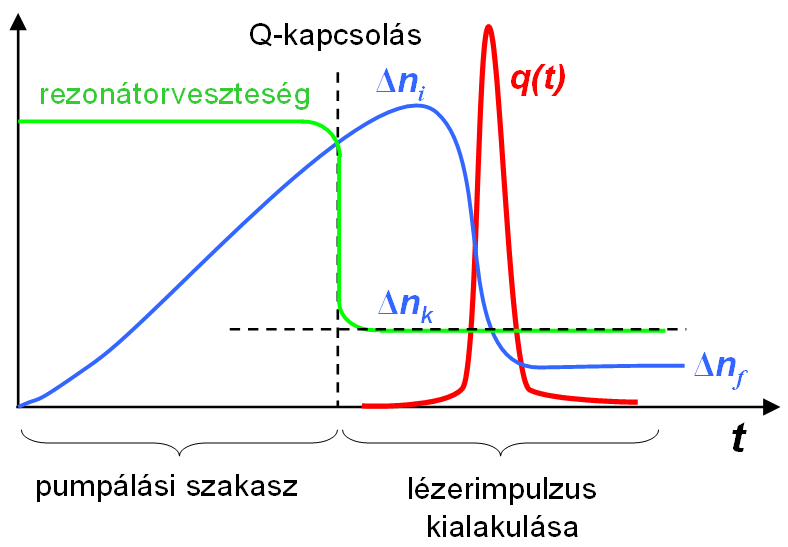
7.5. ábra. A populációinverzió, a rezonátorveszteség és a fotonszám időbeli változása.
A Q-kapcsolás dinamikai tárgyalásához tételezzünk fel lépcső alakú függvénnyel leírható pumpálást, azaz Rp = 0, ha t < 0, majd t > 0 esetében Rp = állandó értékű. A rezonátorban elhelyezett kapcsoló a 0 < t < tp időintervallumban zárva van. Ezen feltételeket használva a populációinverzió időbeli változása a (7.1) egyenlet megoldásával számolható, azaz
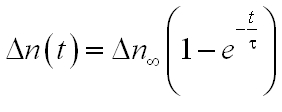 |
, | (7.23) |
ahol a Δn∞ aszimptotikus érték:
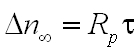 |
. | (7.24) |
melyet a dΔn/dt = 0 feltétel mellett kapunk meg. A (7.23)-ból látható, hogy a tp pumpálási időnek a τ-val hasonló nagyságrendbe kellene esni. Ezzel szemben a gyakorlatban tp >> τ, azaz a pumpálás egy idő után már nem eredményez jelentős populációinverziót, így a bepumpált energiát részben spontán emisszió formájában veszítjük el. A (7.24) kifejezésből látható, hogy nagy populációinverzió elérése hosszú élettartamú nívót igényel. Ezért a Q-kapcsolás tiltott dipólátmeneteknél alkalmazható hatékonyan, ahol a τ értéke milliszekundumos nagyságrendbe esik. Ez az eset fennáll a legtöbb szilárdtest lézer esetében (pl. Nd, Yb, Er) és néhány gázlézernél (pl. CO2). Más lézereknél a Q-kapcsolási technikát nem érdemes alkalmazni.
Gyors kapcsolást feltételezve a (7.1) sebességegyenlet az alábbi alakra egyszerűsödik:
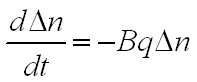 |
, | (7.25) |
azaz az Rp és Δn/τ tagok elhanyagolhatók. A fotonszám változását meghatározó (7.2) egyenlet viszont változatlan formában érvényes. Az egyenleteket megoldva kapjuk a 7.5. ábrán látható görbéket. Amikor a rezonátor vesztesége lecsökken, azaz a Q jósági tényezője megnő, a populációinverzió még egy kicsit növekszik, eléri a Δni maximális értéket. Ezután elkezd igen gyorsan csökkenni, és amikor eléri a Δnk küszöbértéket, akkor lesz a fotonszámnak éppen maximuma, ahogy a relaxációs oszcillációnál is már láttuk. Ettől az időponttól kezdve a rezonátorveszteség már nagyobb, mint az erősítés, ezért a fotonszám is csökkenni kezd a zéró körüli értékre. Közben a populációinverzió eléri a minimális Δnf értéket. A tárolt energia közelítő értéke, ami impulzus formájában sugárzódik ki:
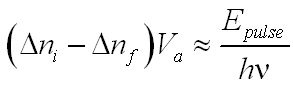 |
. | (7.26) |
Forgó tükör
A legegyszerűbb megoldás a rezonátor veszteségének a gyors kapcsolására, ha a rezonátor egyik, alapvetően rögzített helyzetű végtükrét megforgatjuk a rezonátor tengelyére merőleges tengely körül (7.6. ábra). Nagy Q értéke csak akkor van a rezonátornak, ha a forgó tükör síkjára merőleges tengely párhuzamossá válik a rezonátor tengelyével. Ez a megoldás bármely lézerhullámhossz esetén használható. A hátránya egyrészt, hogy elég zajos, másrészt a forgatás sebessége rendszerint nem tesz lehetővé igen gyors kapcsolást. Például, ha egy lézernyaláb divergenciája néhány mrad, akkor a magas Q értékét akkor kapunk, ha a tükör a tökéletes helyzettől maximum 1 mrad-ra fordul csak el. Ha a forgatás szögsebessége 24000 fordulat/perc, akkor a magas Q érték kb. 400 ns-ig áll fenn. Ez a lassú kapcsolási idő rendszerint többes impulzusokat eredményez a lézer kiemenetén.
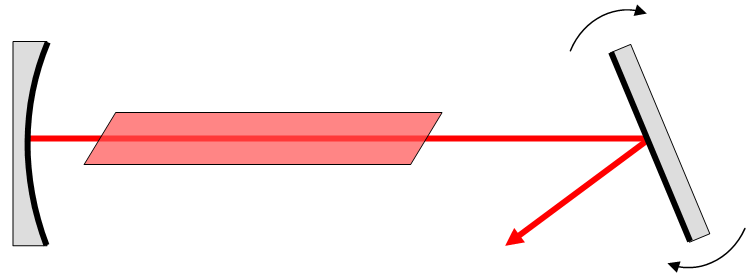
7.6. ábra. Q-kapcsolás megvalósítása forgótükörrel.
Elektrooptikai Q-kapcsolás
A gyors Q-kapcsolás elérésére alkalmazzák a 7.7. ábrán látható, egy elektrooptikai effektuson, rendszerint a Pockels-effektuson alapuló megoldást. A Pockels-cella fő eleme egy nemlineáris, kettőstörő kristály, pl. KD*P vagy lítium-niobát, ha a látható, illetve a közeli infravörös tartományban illetve kadmium-tellurid, ha a közép infravörös tartományban működik a lézer. Ha a kristályra feszültséget kapcsolunk, akkor a törésmutatói megváltoznak. Az indukált kettőstörés nagysága arányos a feszültséggel.
A Q-kapcsolás megértéséhez induljunk ki abból, hogy lineárisan poláros fény esik be balról a polarizátorra, mely átengedi a fényt. A Pockels-cellára olyan mértékű feszültséget kapcsolunk, hogy cirkulárisan polárossá teszi a fényt. A végtükörről visszaverődő, továbbra is cirkulárisan poláros fény a Pockles-cellán való áthaladáskor ismét lineárisan polárossá válik, csak az eredeti polarizációs irányához képest 90 fokkal elfordulva. Ez azt eredményezi, hogy a polarizátoron már nem tud átmenni, így nem alakul ki a visszacsatolás. Amikor viszont lekapcsoljuk a feszültséget a Pockels-celláról, akkor nem forgatja el a fény polarizációs síkját, így létrejön a visszacsatolás és a lézerműködés. A Pockels-cellára kapcsolt feszültség tipikus értéke 1-5 kV között van, és kapcsoló kb. 20 ns alatt kapcsol ki.
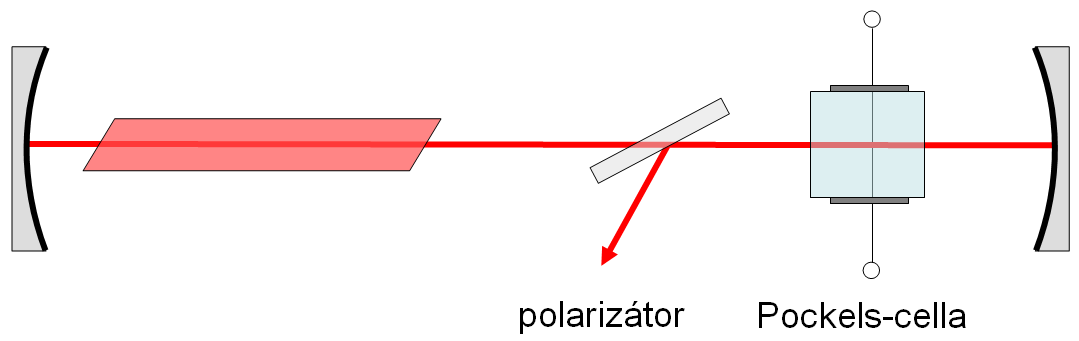
7.7. ábra. Elektrooptikai Q-kapcsolás.
Akusztooptikai Q-kapcsolás
Az akusztooptikai kapcsoló egy átlátszó anyagból van, pl. ömlesztett kvarcból, ha a látható és a közeli infravörös hullámhossztartományban működik a lézer. Ebbe az üveghasábba egy rádiófrekvenciás jellel meghajtott piezoelektromos tranduceren keresztül ultrahangot csatolunk be. Az üveghasábnak a transducerrel átellenes oldala úgy van kialakítva, hogy elnyelje az akusztikus hullámokat, így haladó akusztikus hullámok vannak csak jelen az üveghasábban. Az akusztikus hullámok törésmutató-változást okoznak az üveghasábban egy fotoelasztikus effektuson keresztül. Mivel a hullámok periodikusak, így a törésmutató-változás is periodikus lesz, azaz egy fázisrács alakul ki. Mivel az akusztikai hullámok a hangsebességgel haladnak az üvegben, így a fázisrács is mozog.
Ha a modulátorra rákapcsoljuk a rádiófrekvenciás jelet, akkor a kialakuló fázisrács a rezonátorban terjedő fény egy részét diffraktálja (7.8. ábra). Ez jelentős veszteséget okoz a rezonátorban, és nem indul be a lézerműködés. Ellenben, ha lekapcsoljuk a rádiófrekvenciás jelet, akkor a Q-kapcsolás megvalósul.
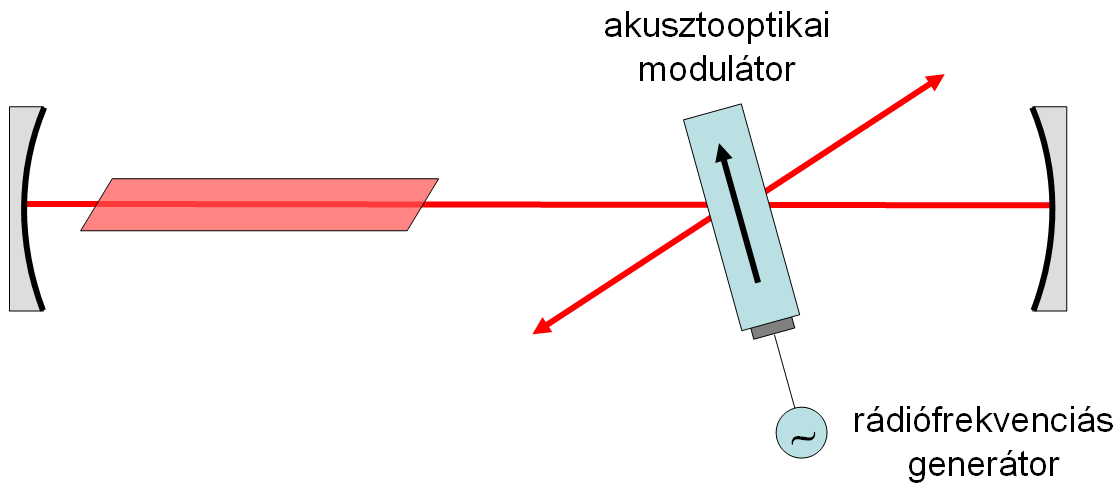
7.8. ábra. Q-kapcsolás akusztooptikai modulátorral.
Telítődő abszorbens
Az eddig említett Q-kapcsoló eszközök aktív Q-kapcsolók, mivel szükségük van egy külső jelforrásra, amely őket ki- illetve bekapcsolja. Most viszont egy passzív Q-kapcsoló eszköz működési mechanizmusát vizsgáljuk meg, mely a telítődő abszorbens nemlineáris viselkedésén alapul. A telítődő abszorbens egy olyan anyag (pl. bizonyos festékek), amely elnyeli az adott hullámhosszúságú lézerfényt és már kis intenzitásoknál is telítődik, azaz zérussá válik az abszorpciója.
Tételezzük fel, hogy kezdetben a rezonátorban elhelyezett abszorbens a fény 50%-át elnyeli, így nagy a rezonátor vesztesége (7.9. ábra). Ennél fogva nem indul be a lézerműködés, a pumpálás hatására viszont folyamatosan nő a populációinverzió. Amikor aztán elkezd működni a lézer a spontán emisszió okozta zajból felépülve, a festék az elnyelt lézerfény hatására nagyon gyorsan telítésbe jut, kifehéredik. Ekkor a lézerfény akadálytalanul át tud haladni rajta, visszaverődik a rezonátor végtükréről, így a rezonátor jósági tényezője hirtelen magassá válik, megtörténik a Q-kapcsolás.
A festékek telítődő abszorbensként való alkalmazásának hátránya, hogy bizonyos számú impulzus után molekula szerkezeti változások, fotokémiai degradáció következik be. Ezért napjainkban már szilárdtest telítődő abszorbenseket alkalmaznak.
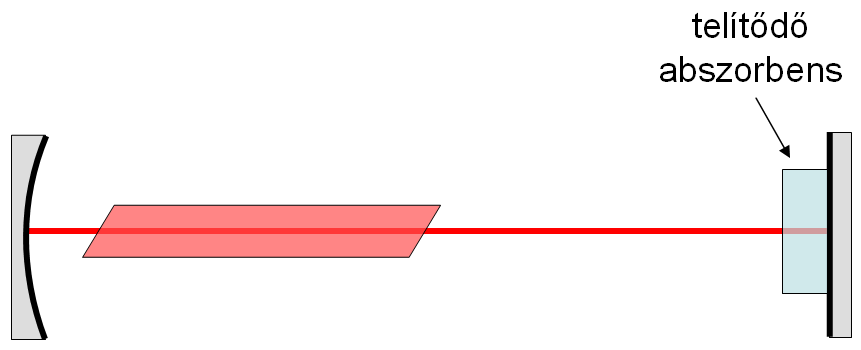
7.9. ábra. Q-kapcsolás megvalósítása telítődő abszorbenssel.
Az erősítés-kapcsolás a Q-kapcsoláshoz hasonlóan lehetővé teszi rövid (10-500 ns időtartamú), nagy csúcsteljesítménnyel rendelkező impulzusok előállítását. A Q-kapcsolástól eltérően itt nem a rezonátorveszteséget, hanem az erősítést kapcsoljuk fel gyorsan egy nagy értékre. Az erősítés-kapcsolást úgy érjük el, hogy a pumpaimpulzus olyan gyors, hogy a populációinverzió és ennél fogva az erősítés a küszöbértéket jelentősen túlhaladja, miközben a rezonátorban a fotonszám még nem nő meg, azaz az indukált emisszióval nem tudja jelentősen csökkenteni a populáció inverzió értékét.
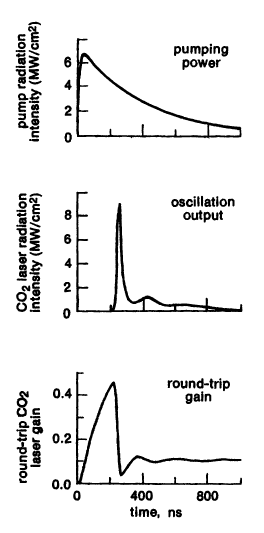
7.10. ábra. Egy impulzus gerjesztésű CO2 lézer számolt erősítés-kapcsolása [7.1].
A jelenség kvalitatív értelmezéséhez tekintsük ismét a 7.1. ábrát. Ha a pumpa most csak t = 5 μs-ig tart, akkor a fénykibocsátás csak egy impulzust fog jelenteni, mivel a következő impulzus már nem jön létre, hiszen a küszöb alatt lesz a populációinverzió értéke t = 5 μs-tól. A relaxációs oszcilláció és az erősítés-kapcsolás között a pumpaimpulzus időbeli hosszán kívül az is a különbség, hogy az Rp csúcsértéke jóval nagyobb a folytonos pumpáláshoz képest. A pumpálási sebesség csúcsértékétől függően a populációinverzió maximuma 4-10-szerese a küszöbértéknek, miközben a relaxációs oszcillációnál a 7.1. ábrán csak 1,5-szerese. A lézersugárzás a maximális értékét a rezonátor átlagos τc fotonélettartamának az 5 - 20-szoros ideje alatt éri el, ebből következően a pumpaimpulzusnak ettől rövidebb időtartamúnak kell lenni.
A legáltalánosabb példa az erősítés-kapcsolás alkalmazására az elektromos impulzussal keresztirányban gerjesztett atmoszférikus nyomású TEA CO2 lézer. A rezonátor élettartam tipikus értéke τc = 30 ns. Feltételezve, hogy a lézer felépülési ideje 10-szer hosszabb, akkor a gerjesztő impulzusnak kb. 300 ns hosszúnak kell lenni. Ez a gyakorlati megvalósítással jól egyezik. Egy másik példa, amikor rhodamin 6G festéket, mint aktív közeget tartalmazó lézert egy 0,5 ns-os impulzusokat kibocsátó N2 lézerrel gerjesztünk. Ebben az esetben a felső lézernívó élettartama 5 ns. Ennek eredményeképpen 100 ps-os lézerimpulzusokat kapunk.
Tekintsünk egy lézerrezonátort, melyben időben egyszerre több longitudinális módus is működik. Általános esetben a módusok egymáshoz képesti fázisa véletlenszerű, így a kijövő lézernyaláb intenzitása véletlenszerűen ingadozik. A 7.11. ábrán N = 51 longitudinális módus összegzésével kapott fényintenzitás látható. A módusoknak azonos az amplitúdója, a fázisa véletlenszerű. A módusok közötti frekvenciatávolság azonos, értéke Δν, és a frekvenciaspektrum szélessége Δν L = NΔν. Vegyük észre, hogy bár a fázisok véletlenszerűen változnak, impulzusokat látunk, melyek amplitúdója véletlenszerűen változik. Az impulzus szélessége Δτ p = 1/Δν L , mely a Fourier-sorok jellemzője. Szintén ebből adódik, hogy a véletlenszerű impulzussorozat τ p = 1/Δν időközönként ismétlődik. Azon lézerek esetében, ahol széles a frekvenciaspektrum (pl. festéklézerek, Ti:zafír lézer), az impulzusok nagyon rövid időtartamúak, amit a fotodetektoraink nem tudnak feloldani.
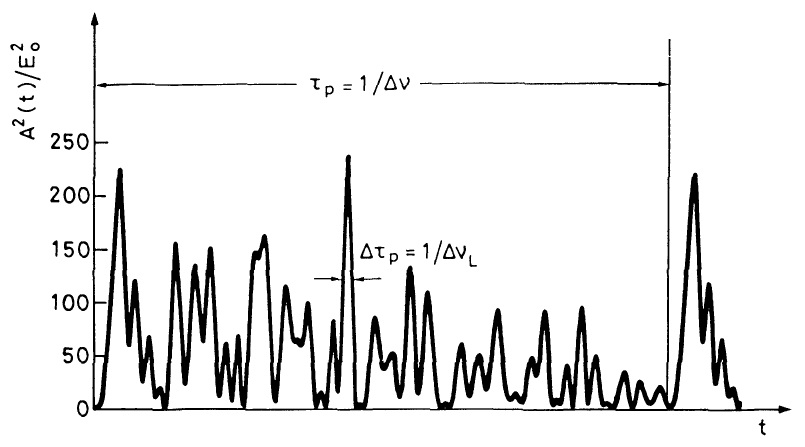
7.11. ábra. 51, egymáshoz képest véletlen fázissal rezgő, azonos amplitúdójú longitudinális módus eredőjeként kapott fényintenzitás [7.1].
A továbbiakban tételezzük fel, hogy a longitudinális módusok egymáshoz képesti fázisa időben állandó. Azokat a lézereket, amelyekre ez a feltétel igaz, módusszinkronizált lézereknek, és azt a folyamatot, amivel elérjük e feltétel teljesülését, módusszinkronizációnak nevezzük.
Tekintsünk 2n+1 longitudinális módust, amelyeknek az amplitúdója ugyanaz, E0. Tételezzük fel, hogy két szomszédos (az l-edik és l-1-edik) módus fázisa közötti különbség
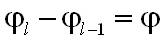 |
, | (7.27) |
ahol φ állandó értékű. A lézerből kilépő nyaláb térerőssége a módusok térerősségének összege:
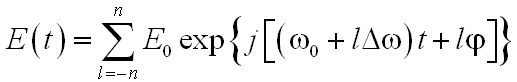 |
, | (7.28) |
ahol ω0 a központi módus körfrekvenciája, és Δω a szomszédos módusok közötti körfrekvencia-különbség. Az egyszerűség kedvéért a központi módus fázisa zérus. A (7.28) összeg átírható az alábbi alakra:
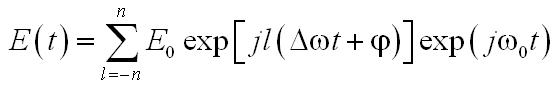 |
. | (7.29) |
A (7.29)-ből láthatjuk, hogy az eredő térerősség szorzata egy ω0 frekvenciájú vivőhullámnak és egy időfüggő amplitúdónak. A 7.12. ábra mutatja, hogy ha 7 módust adunk össze, akkor a (7.29)-ből számolt intenzitás hogyan függ az időtől. A 7.11. ábrától eltérően időben jól elkülönülő, jóval nagyobb csúcsintenzitású impulzusokat kaptunk. Most is az impulzusok időben periodikusan követik egymást.
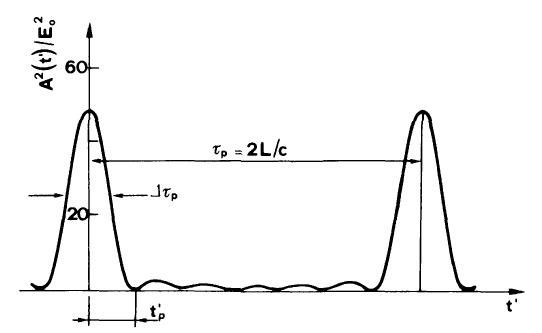
7.12. ábra. Módusszinkronizáció esetén 7 db egyenközű, longitudinális módus összeadásaként előálló intenzitás az idő függvényében [7.1].
Korábban már megállapítottuk, hogy a Fourier-sorok elméletéből következik, hogy az impulzusok követési ideje τ p = 1/Δν. Mivel a Δν = c/2L, ahol L a rezonátor hossza, így kapjuk, hogy τp = 2L/c, ami éppen a rezonátor körülfutási ideje. Ennek alapján a módusszinkronizált lézer működését úgy is felfoghatjuk, mintha egy impulzus haladna a rezonátorban oda-vissza, és amikor a kicsatoló tükörhöz lép, ott egy kis része kilép a rezonátorból. Így áll elő egy impulzussorozat.
Ebben a képben a módusszinkronizáció elvét úgy értelmezhetjük, hogy a rezonátorban az egyik tükör elé egy fényzárat teszünk, ami 2L/c időnként nyit ki. Ha a fényzár akkor nyit ki, amikor a 7.11. ábrán látható, legintenzívebb zajimpulzus ér oda, és a zár nyitvatartási ideje körülbelül annyi, mint a zajimpulzus időtartama, akkor az impulzussorozatból csak ez a legintenzívebb impulzus fog kierősödni, létrehozva a módusszinkronizációt.
A Q-kapcsoláshoz hasonlóan itt is két csoportra oszthatók a módszerek. Az aktív módusszinkronizációnál az effektust létrehozó optikai elemet külső jelforrásból kell vezérelni, míg a passzív módusszinkronizáció egy telítődő abszorbenssel vagy egy megfelelő anyag nemlineáris törésmutatójának változásával áll elő.
Aktív módusszinkronizáció
Aktív módusszinkronizációt három alapvető módszerrel hozhatunk létre: amplitúdó modulátorral, fázismodulátorral és az erősítés periodikus modulálásával a rezonátor ismétlési frekvenciáján (szinkronpumpálás). Az amplitúdó modulátoros technika a legáltalánosabban elterjedt módszer, ezért csak ezt tárgyaljuk. Az időképbeli leírási módot használjuk, mert abban könnyebben megérthető a lényege.
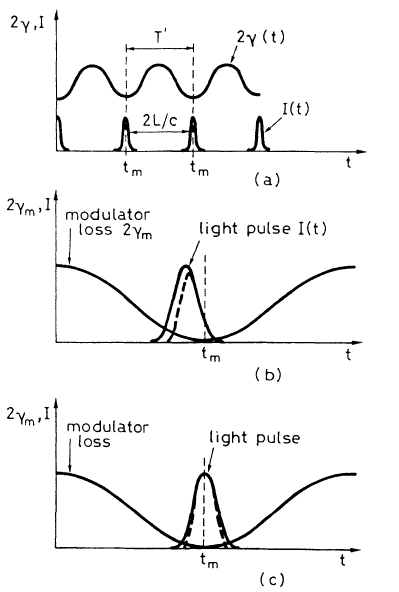
7.13. ábra. Időképbeli leírása az amplitúdó modulátoros módusszinkronizálási módszernek. (a) A stabil állapot feltétele. (b) Ha előbb érkezik az impulzus, minthogy az erősítés a minimumra csökkent volna. (c) Éppen az erősítés minimumánál érkezik az impulzus, és ekkor időben megrövidül [7.1].
A rezonátorban fellépő veszteséget éppen a rezonátor körülfutási ideje szerint moduláljuk (7.13.a. ábra). Feltételezzük, hogy a modulátor a rezonátor egyik végén van elhelyezve. A stabil működés akkor áll fenn, ha az impulzusok akkor érnek a modulátorhoz, amikor a legkisebb a veszteség (7.13.a ábra). Ha az impulzus kicsit előbb ér (7.13.b ábra), akkor a nagyobb veszteség az impulzus végét lefaragja, így következőben már megfelelőbb időben ér a modulátorhoz. A 7.13.c. ábra azt mutatja, hogy elvileg minden körüljárás után rövidebb lesz az impulzus időtartama, azaz zérushoz tart. Azonban tudjuk, hogy minél rövidebb az impulzus, annál szélesebb a spektruma. Így az erősítő véges spektrális sávszélessége megakadályozza, hogy egy adott értéknél rövidebb legyen az impulzus időtartama. Modulátorként a fejezetben már többször említett Pockels-cellát használják a 7.7.ábrának megfelelő elrendezésben.
Passzív módusszinkronizáció
A passzív módusszinkronizációnak négy fő típusa van: (i) nagyon rövid élettartamú felső nívóval rendelkező telítődő abszorbens (pl. festékmolekula), (ii) Kerr-lencsés módusszinkronizáció, mely egy átlátszó, nemlineáris optikai anyagban bekövetkező önfókuszálódásra épül, (iii) lassan telítődő abszorbens, (iv) additív módusszinkronizáció, mely egy nemlineáris anyagban bekövetkező önfókuszálódásra alapul, ami egy segédrezonátorban van elhelyezve. A segédrezonátor körülfutási ideje azonos a főrezonátoréval. A két rezonátorból érkező impulzusok interferenciája okozza az impulzusrövidülést. Mivel a hullámhossz nagyságrendjébe esően kell a két rezonátor hosszának megegyezni, ezért e technika nem nagyon terjedt el, és így nem tárgyaljuk részletesebben. A lassan telítődő abszorbens működését sem vizsgáljuk részletesebben.
A telítődő abszorbens esetében ismét a 7.11. ábrát vegyük alapul. Míg a kisebb amplitúdójú impulzusok esetében nem telítődik az abszorbens, addig a legintenzívebb impulzus esetében igen. Így a legintenzívebb impulzusnál lesz a legkisebb a rezonátorveszteség, így ez az impulzus erősödik meg legjobban.
A Kerr-lencsés módusszinkronizáció alapja, hogy bizonyos anyagok (pl. kvarc, zafír) esetében a nemlineáris törésmutató (n2) jelentősebb, azaz az anyag törésmutatója
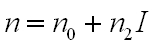 |
. | (7.30) |
Az n2 értéke ömlesztett kvarcra 4,5·10-16 cm2/W és zafírra 3,45·10-16 cm2/W. A törésmutató intenzitásfüggése úgy ismert, mint az optikai Kerr-effektus. Tételezzük fel, hogy a lézernyaláb intenzitás-eloszlása nem homogén, hanem pl. Gaussos. Ez azt jelenti, hogy a nyaláb közepén nagyobb az intenzitás, mint a szélén, és így nagyobb a törésmutató is. Ez viszont azt eredményezi, hogy a fázistolás keresztirányú függése egy gyűjtőlencsének megfelelő lesz.
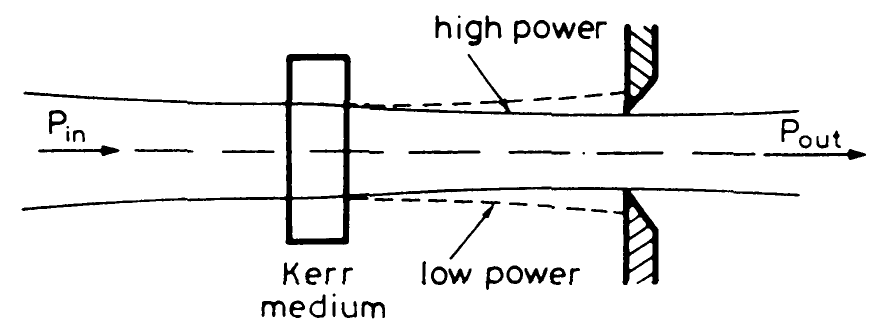
7.14. ábra. Az optikai Kerr-effektus miatt nagyobb intenzitásoknál gyűjtőlencse-hatás alakul ki a közegben [7.1].
Ha a Kerr-hatásra érzékeny közeg után egy apertúrát helyezünk el (7.14. ábra), akkor a nagyobb intenzitású nyaláb jobban összefókuszálódik, így az apertúra nem okoz számára veszteséget, ellentétben a gyengébb intenzitású nyalábbal, azaz a nagyobb intenzitásnál kisebb a veszteség, mint a kisebb intenzitásnál. Ezáltal a módusszinkronizáció kialakul. A Kerr-effektus időtartama nagyon rövid, így a legrövidebb impulzusokat előállító lézerekben ezt a technikát használják.
A rezonátorkiürítési technika lehetővé teszi, hogy a lézerben tárolt energiát a rezonátor körülfutási idő alatt kiürítsük a rezonátorból. E technika elvét mutatja a 7.15. ábra, ahol a rezonátor két végtükre 100%-os reflexiójú, és a lézernyalábot egy speciális optikai elemmel csatoljuk ki. E speciális optikai elemnek a reflexióképessége időben változik, azaz R = R(t). Alapvetően R = 0%, de a kicsatolás idejére R = 100% lesz.
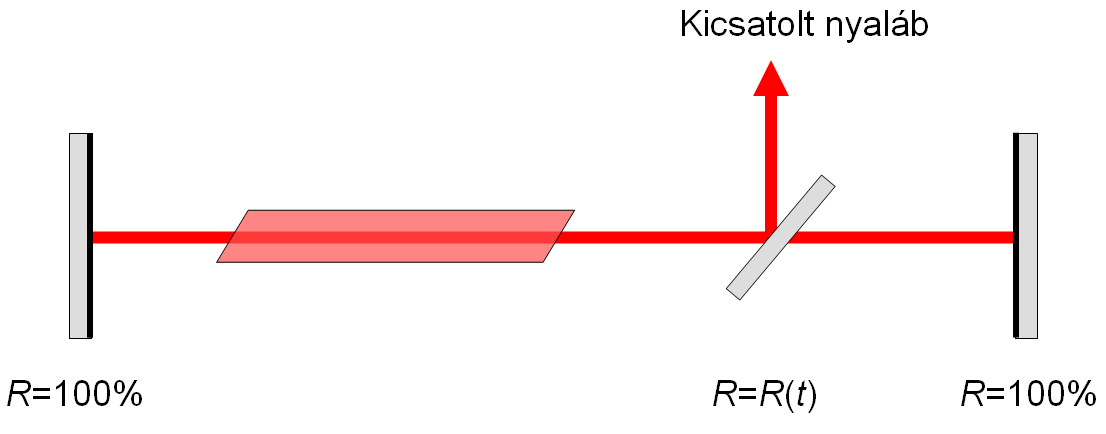
7.15. ábra. A rezonátorkiürítésen alapuló lézer felépítése.
Az impulzuslézerrel pumpált módusszinkronizált lézereknél a kicsatoló elem gyakran Pockels-cella, és a rezonátorbeli megvalósítás a 7.7. ábrán látható, melyet a Q-kapcsolásnál is alkalmaznak. A Pockels-cellát akkor nyitják ki, amikor a rezonátorban a módusszinkronizáció miatt az impulzus éppen a maximumát éri el. Ily módon egy nagyintenzitású impulzust csatolnak ki.
A folytonos üzemű módusszinkronizált lézereknél egy impulzussorozatot állíthatunk elő, melynek az ismétlési frekvenciája nem a módusszinkronizáció folyamata során előálló impulzussorozat frekvenciája, hanem annál kisebb, a kicsatoló elem ismétlési frekvenciájával egyezik meg. Így kisebb ismétlési frekvenciával, de jóval nagyobb csúcsteljesítményű impulzusokat kapunk összevetve a tisztán csak a módusszinkronizációval kapott impulzusokkal.
Írja fel a populációinverzió időfüggését megadó egyenletet! Mitől függ a csillapodási idő és a rezgés körfrekvenciája?
Rajzolja le Q-kapcsolás esetén a populációinverzió, a rezonátorveszteség ésa ftonszám időbeli válzozását!
Milyen Q-kapcsolási módszereket ismer!
Mit jelent az aktív módusszinkronizáció kifejezés?
[7.1] O. Svelto, D. C. Hanna: Principles of lasers (4th ed, Springer, 1998)
[7.2] R. W. Hellwarth: Control of fluorescent pulsations, in Advances in Quantum Electronics (J. R. Sinder ed.) (Columbia Univ Press, 1961), pp. 334-341.
[7.3] T. J. Kane, R. L. Bayer, Optics Letters 10, 65 (1985)
[7.4] D. F. Nelson, W. S. Boyle, Applied Optics 1, 181 (1962)
Tartalom
A lézerműködéshez ideális aktív anyag nagy abszorpciós együtthatóval, keskeny fluoreszcencia átmenettel és nagy kvantum hatásfokkal rendelkezik. Egy szilárd hordozóba (kristály vagy üveg) szennyezésként bevitt átmeneti fémek, ritka földfémek vagy aktinoidák rendelkeznek ilyen tulajdonságokkal. Ezen elemek belső, nem betöltött elektronsávjait a külső, töltött elektronsávok védik a hordozóanyag hatásától, és ezért szabad ionokként viselkednek. A ritka földfémek esetén a 3d-3d átmenetek, míg az átmeneti fémek esetén a 4f-4f átmenetek játszanak fontos szerepet. A lézerműködés szempontjából fontos három paraméter: a gerjesztett állapot élettartama (τf), az emissziós hatáskeresztmetszet (σ) és az erősítés sávszélessége (Δν). A lézerműködéshez szükséges küszöbérték fordítottan arányos a gerjesztett állapot élettartamával és a hatáskeresztmetszet szorzatával, így annak eldöntéséhez, hogy egy lézer működhet-e folytonos üzemben, szükséges tudni a τfσ szorzat értékét. A sávszélesség a hangolható lézereknél határozza meg a hangolási tartományt és a minimális impulzushosszt, amit módusszinkronizációval lehet létrehozni. Az átmeneti fémek pl. széles emissziós sávszélességgel rendelkeznek, ezért előszeretettel alkalmazzák hangolható, rövid impulzusú lézerekben. Összefoglalva, a szilárdtestlézerek fizikai paramétereit meghatározó négy szempont:
(i): A hordozóanyag mechanikai, termális és optikai, valamint a rácsszerkezet mikroszkopikus tulajdonságai.
(ii): A lézerműködést biztosító szennyezőanyag spektrális tulajdonságai.
(iii): Az aktív közeg optikai pumpálásának geometriai, spektrális és termális tulajdonságai.
(iv): Az optikai rezonátor geometriája és egyéb fizikai tulajdonságai, módusszelekció, módusszinkronizáció, stb.
A hordozóanyaggal szemben támasztott egyik alapvető követelmény a magas optikai minőség. A törésmutató térbeli inhomogenitása a keletkező lézer nyalábprofilját befolyásolja: a lézer nem az alkalmazások szempontjából ideális TEM00 alapmódusban fog üzemelni. A hordozó mechanikai és termális tulajdonságai, különösen nagy lézerteljesítmények esetén válnak kritikussá. A lézer teljesítmény-, intenzitás- és irány-stabilitását javíthatjuk a hordozóban fellépő mechanikai feszültségek csökkentésével illetve hőmérsékletstabilizációval. A törésmutató hőmérsékletfüggése miatt a hőmérsékletstabilizáció a lézernyaláb profilját is befolyásolja. Ez különösen kritikus azon lézerek esetében, ahol a hullámhossz hangolása a hőmérsékletváltozáson alapszik. A kristályszerkezet megválasztásánál fontos, hogy a szennyező atomok homogén módon tudjanak diffundálni a hordozóba. Az üvegek az egyik legfontosabb hordozók. Nagy méretben és kitűnő optikai minőségben állíthatók elő, ami a nagy teljesítményű lézerek esetén különösen fontos paraméter. A kristályos hordozókhoz képest azonban a fluoreszcencia átmenetek kiszélesednek (ezáltal a pumpálási küszöbérték megnő), továbbá a hővezetési tulajdonságaik is kedvezőtlenebbek, ami nyalábtorzuláshoz vezethet. Az oxidok kristályszerkezetű hordozók, ezért az üvegekhez képest kitűnő termális tulajdonságokkal rendelkeznek, és a fluoreszcencia vonalak kevésbé kiszélesedettek. Az optikai tulajdonságaik azonban tipikusan rosszabbak, mert nagy méretű, jó minőségű kristályt növeszteni nagyon nehéz. A kristály homogén szennyezése további technológia kihívást jelent. Legfontosabb hordozóként alkalmazott oxidok az Al2O3, ami Cr3+ ionokkal szennyezve a rubinlézer aktív anyaga; a Y3Al5O12 (yttrium-alumínium-granát: YAG), ami a Nd3+ ionokkal szennyezve a neodímiumlézerek aktív anyaga; a YAlO3 (YAP), amit Nd3+, Er3+, Ho3+ és Tm3+ ionokkal lehet szennyezni és a YAP kristály anizotróp jellege miatt számos előnnyel rendelkezik; és a La2O2S (LOS), amit neodímiumionokkal szennyezve az 1.075 μm-es hullámhosszon tudunk lézerműködést előidézni. További hordozóként lehet foszfátokat, szilikátokat, fluoridokat és kerámiákat alkalmazni.
A szilárdtestlézerekben szennyezőanyagként ritka földfémeket, átmeneti fémeket és aktinoidákat alkalmaznak. A ritka földfémekben a 4s, 4p, 4d, 5s, 5p és 6s pályák teljesen betöltöttek, de a 4f pálya csak részlegesen betöltött. A Nd atomban pl. 4, az Er atomban 12 elektron van a 4f pályán. Kristályokban ezek az atomok tipikusan három értékű, trivalens ionokat képeznek. Ennek során az atomok elvesztik a 6s pályán lévő két elektronjukat, valamint a 4f pályáról még egyet. Így pl. a Nd3+ elektronszerkezete: ...4f35s25p6, az Er3+ ioné pedig ...4f115s25p6. Mivel a külső, zárt pályák (5s és 5p) árnyékolják a belső 4f pályán lévő, és a lézerműködésben fontos szerepet játszó átmeneteket, a szennyező atomok fluoreszcencia spektruma keskeny marad, és csak enyhén függ a hordozóközegtől. Az aktinoidák hasonlítanak a ritka földfémekre, de esetükben az 5f pálya van részlegesen betöltve és árnyékolva a 6s és 6p pályák által. Az átmeneti fémek két legfontosabb eleme a króm és a titán. A króm elektronszerkezete: Cr:...3d54s. A trivalens állapotot három elektron leadásával éri el: Cr3+:...3d3. Mivel a krómban külső, betöltött pályák nem védik a betöltetlen pályákat, az optikai paraméterek erősen függnek a hordozótól. A titánnak hasonló az elektronszerkezete de 6 elektron helyett csak 4 elektronja van a külső pályákon: Ti:...3d24s2. Trivalens állapotban a 3d pályán egy elektronja lesz: Ti3+:...3d.
A rubinlézer aktív anyaga a rubinkristály Cr3+:Al2O3 , azaz olyan Al2O3 kristály, amelyben az Al3+ ionok kis koncentrációban (0,05 %) Cr3+ ionokra vannak kicserélve. A rubinlézer háromnívós rendszer, amelynek energianívó vázlata a 8.1. ábrán látható. A lézerműködéshez nagy pumpáló teljesítményre van szükség, ami jelentős hőterhelést jelent mind a lámpára, mind a rubinrúdra nézve. Ezért a rubinlézerek tipikusan impulzusüzemben működnek. A villanólámpával gerjesztett rubinlézerben az alapállapotban (4A2) lévő krómionok a nagyon rövid élettartamú (50 ns), de nagy sávszélességű gerjesztett állapotból (4F1 és 4F2) sugárzásmentes átmenettel kerülnek a 3 ms élettartamú 2E állapotba. Fontos megemlíteni, hogy az 4F2 és 4F1 energianívók nagyon szélesek (1000Å), és látható (zöld: 18000 cm-1) és közeli UV (kék: 25000 cm-1) fotonokkal gerjeszthetők. Ezért jól gerjeszthetők villanólámpával, melyek spektruma közelíthető a 7000 K és 9000 K hőmérsékletű feketetest sugárzók spektrumához. A metastabil 2E állapot a kristályrács szimmetriatulajdonsága miatt két energianívóra (2Ā és Ē) hasad, amelyek távolsága 29 cm-1, és a lézerátmenet felső energianívóit képezik. A valóságban a két átmenet közül az R1 jelzésű 694,3 nm-es átmeneten jön létre az indukált emisszió, a lézer spektrumában ez a vonal lesz a domináns. Ennek oka, hogy termális egyensúlyban a 2Ā és Ē energianívók betöltöttsége eltérő. A populációk különbségét a Boltzman faktor adja meg (κ=exp(ΔE/kT)), amelynek értéke szobahőmérsékleten κ=0,87, így az R1 átmenethez tartozó Ē energianívó hamarabb éri el a lézerműködéshez szükséges küszöbértéket, mint az R2.
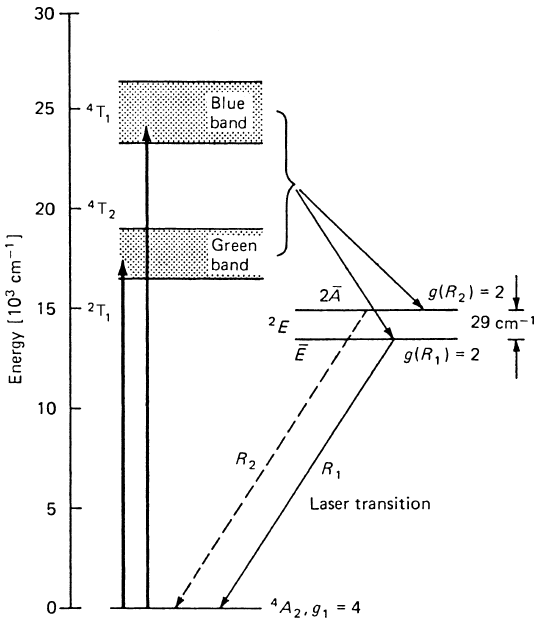
8.1. ábra. A rubinlézer energianívó vázlata. [8.1]
A Nd3+:YAG lézer a gyakorlati alkalmazás szempontjából az egyik legfontosabb lézertípus. A Nd3+:YAG kristályban a Y3+ ionoknak kb. 1 %-át helyettesítik Nd3+ ionokkal. Magasabb koncentráció esetén a fluoreszencia élettartam lecsökken és a vonalak kiszélesednek. Mivel a két ritkaföldfém sugara csak 3%-ban tér el egymástól, a Nd ionokkal szennyezett YAG kristály megtartja eredeti mechanikai stabilitását. A kristály előállítási költsége igen magas, ami elsősorban a lassú (0,5 mm/óra) kristálynövesztésnek köszönhető. Energianívó vázlatát a 8.2. ábra mutatja. A lézer 1064 nm-es hullámhosszon emittál. A lézerátmenet alsó energianívója E2=2111 cm-1-re (0,26 eV) van az alapállapottól ezért betöltöttsége szobahőmérsékleten elhanyagolható (κ=exp(E 2 /kT)=e -10 ): a Nd3+:YAG lézerek négynívós rendszernek tekinthetők. A neodímium ionok abszorpciós hatáskeresztmetszete a YAG kristályban 9×10-19 cm2, ami majdnem két nagyságrenddel nagyobb a rubinkristály abszorpciós hatáskeresztmetszeténél (1,22×10-20 cm2). Ez a magyarázata annak, hogy a küszöbenergia alacsonyabb és a rubinlézerrel ellentétben a Nd3+:YAG lézerek folytonos üzemmódban is használhatók. A kristály számos abszorpciós sávval rendelkezik a 300 nm-900 nm-es tartományban. Ezek közül, a diódalézeres pumpálás lehetősége miatt, a 4I9/2→4F5/2 átmenethez tartozó 808 nm körüli erős abszorpciós sáv az egyik legfontosabb. A Nd:YAG lézerben a 4F3/2→4I11/2 átmenethez tartozó 1064 nm és 1061 nm hullámhosszúságú vonalak emissziós hatáskeresztmetszete a legnagyobb. Szobahőmérsékleten az 1064 nm, míg alacsony hőmérsékleten az 1061 nm-es vonal küszöbértéke az alacsonyabb. Lézerműködés más átmenetek esetén is létrejöhet. A 8.2. ábra szaggatott vonallal három másik lehetséges lézerátmenet is jelöl (1338,1 nm, 1318,7 nm és 946 nm). Ezen átmenetek emissziós hatáskeresztmetszete azonban jóval alacsonyabb és csak az erősebb 1064 nm-es átmenet elnyomásával lehet a lézert ezen hullámhosszakon működtetni.
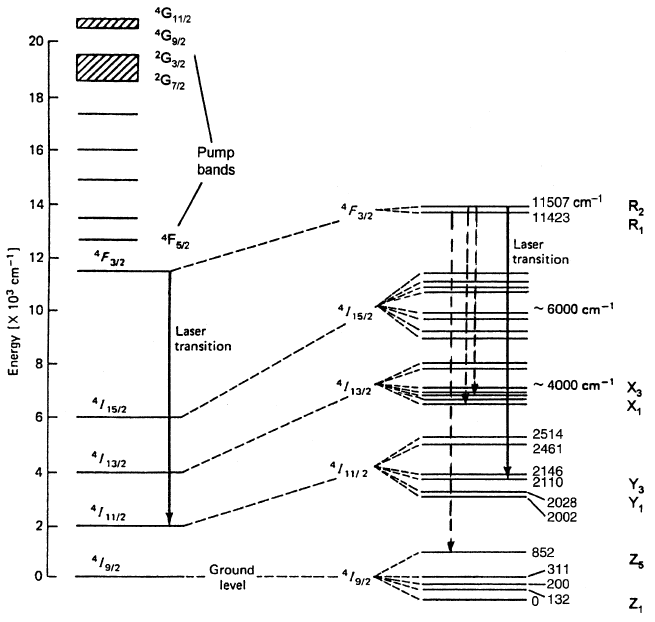
8.2. ábra. A Nd3+:YAG lézer energianívó vázlata. [8.1]
Az üveghordozóknak számos előnyük van más hordozóanyagokkal szemben, amelyek miatt külön érdemes velük foglalkozni. Az üveg izotróp és nagy koncentrációban homogén módón szennyezhető. Nagy méretben, különböző alakban gyártható, kitűnő optikai jellemzőkkel rendelkező alapanyag. A pár mikron átmérőjű optikai szálaktól a több méter hosszúságú és több cm átmérőjű rudakig előállítható. Leggyakrabban P2O5 alapú foszfát- és SiO2 alapú szilikátüvegeket alkalmaznak. Mivel a foszfátüvegek emissziós hatáskeresztmetszete nagyobb és nemlineáris együtthatója kisebb, mint a szilikátüvegé, a nagy teljesítményű Nd3+:üveg lézerekben általában a foszfátüvegeket alkalmazzák hordozóként. A kristályos hordozókkal összehasonlítva hővezető képességük rosszabb, és az emissziós vonalak a Nd3+ ionok és az üveg kölcsönhatása miatt kiszélesednek. Ez a kiszélesedés azonban bizonyos esetekben előnyös is lehet, hiszen rövidebb fényimpulzusok erősítésének lehetőségét biztosítja. A Nd3+::üveg lézer nívószerkezete a Nd3+:YAG lézeréhez nagyon hasonló négynívós rendszer: a legerősebb, 1,06 μm-es vonal a 4F3/2→4I11/2 energianívók közti átmenethez tartozik. A Nd3+:üveg abszorpciós spektruma nagyon hasonló a Nd3+:YAG abszorpciós spektrumára, de a vonalkiszélesedés miatt a csúcsok jóval szélesebbek.
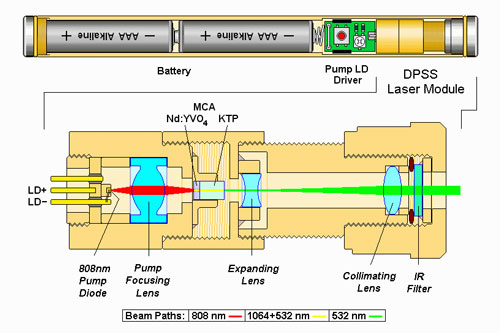
8.3. ábra. A Nd3+:YVO4 lézert tartalmazó frekvenciakétszerezett lézeres mutatópálca felépítése. [8.2]
A Nd3+:YVO4 lézereknél az emissziós hatáskeresztmetszet ötször nagyobb a YAG lézerekénél, és a 809 nm körüli erős és széles abszorpciós sávja különösen alkalmassá teszi a diódapumpálásra. A nagy hatásfokú pumpálásnak köszönhetően aktív anyagként már mm hosszúságú kristály alkalmazható. Ez különösen előnyös a rövid Rayleigh hosszal rendelkező dióda lézerekkel történő gerjesztéshez. A vanadát kettősen törő, egytengelyű kristály, ezért a keletkezett lézerfény lineárisan polarizált. A kettőstörés miatt a kristály gerjesztése is polarizáció érzékeny: a lézerfény polarizációjával párhuzamos gerjesztésre lesz az abszorpciós együttható maximális.
Az erbium lézerek hatásfokuk és teljesítményük alapján nem tartoznának a fontosabb lézerek közé, a működési hullámhosszuk miatt azonban mégis említést teszünk róluk. Kristályos hordozóban (pl. YAG) 2,9 μm, míg foszfátüvegben 1,54 μm hullámhosszakon működnek. Mivel mindkét hullámhosszon a víz jó elnyelő, az erbium lézereket előszeretettel használják orvosi alkalmazásokra. Az Er3+:YAG aktív közegben az erbium koncentrációja nagyon magas (50%). A lézerátmenetet biztosító alsó energianívó (4I13/2) 7000 cm-1 távolságra van az alapnívótól (4I15/2), ezért az Er3+:YAG lézerek négynívós rendszereknek tekinthetőek. Ezen lézerátmenetre vonatkozó emissziós hatáskeresztmetszet 3×10-20 cm2. Az erbium lézerek leghatékonyabban 962 nm-es diódalézerekkel pumpálhatók, amelyek közvetlenül a lézerátmenet felső energianívójára (4I11/2) gerjesztik az Er3+ ionokat.
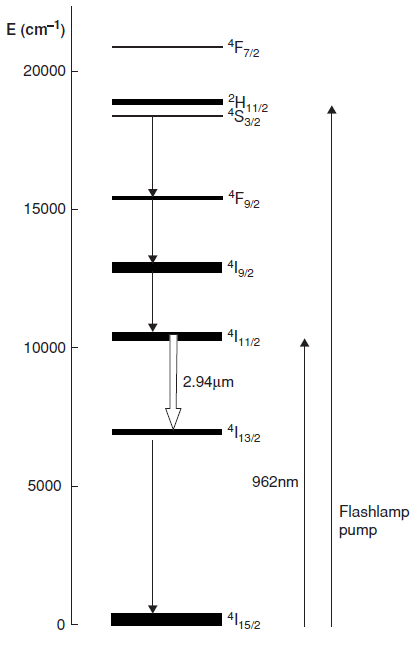
8.4. ábra. A Er3+:YAG lézer energianívói. [8.1]
Az Er3+:üveg lézerek olyan háromnívós rendszerek, amelyekben a lézerátmenet az 1,54 μm hullámhosszúságon valósul meg. Az erbium gyenge abszorpciója miatt az üveget további ritka földfémmel (tipikusan itterbium) kell szennyezni az erbium hatékony gerjesztéséhez. A 8.5. ábra mutatja a két atom közötti energiatranszfert.
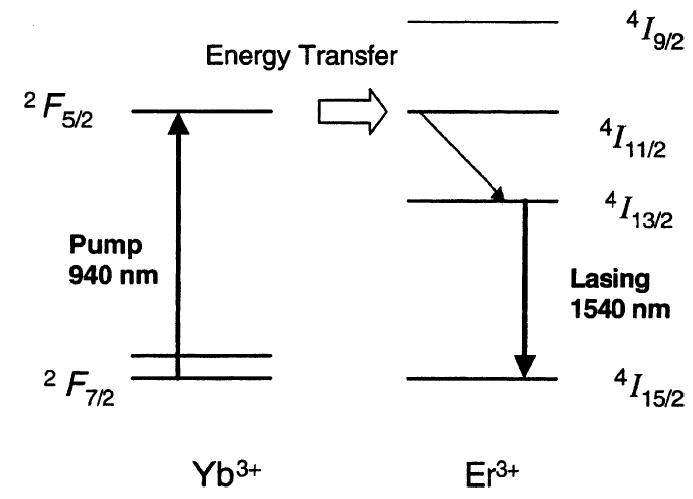
8.5. ábra. Energiatranszfer a Yb3+ és az Er3+ ionok között a háromnívós Er3+:lézer nagyobb hatásfokú gerjesztéséhez. [8.1]
A fejezetben eddig tárgyalt lézereknél az emisszió két, jól meghatározott energianívó között jött létre, ezért a keletkezett lézerfény sávszélessége kicsi volt (a Nd:YAG lézer sávszélessége 120 GHz, azaz 0,45 nm). Alkalmazások szempontjából gyakran fontos olyan lézerek fejlesztése, amelyek kimenő hullámhossza hangolható, vagy széles erősítésüknek köszönhetően rövid impulzusok előállítására alkalmasak. Ez a szilárdtestlézerek esetén a ráccsal való kölcsönhatás révén valósítható meg. Az elektron-fonon kölcsönhatás miatt a energiaszintek kiszélesednek a kristályban, lehetővé téve, hogy a lézerátmenet egy szélesebb energiatartományon valósulhasson meg. Ezeknél a lézereknél a lézerátmenethez tartozó teljes energia megoszlik a fotonok és a fononok között, lehetővé téve a lézer folytonos hangolhatóságát. Ezen lézerek négynívós rendszereknek tekinthetőek.
Az alexandrit lézerekben a BeAl2O4 hordozóanyagot krómmal szennyezik, ezért számos optikai és mechanikai tulajdonsága megegyezik a rubinkristályéval. Az alexandrit abszorpciós spektruma nagyon hasonlít a rubinéhoz: két csúccsal rendelkezik a 410 nm és az 590 nm központi hullámhosszakon. A rombos szerkezetű Cr3+:BeAl2O4 kristály kéttengelyű, kettősen törő kristály, ezért a keletkezett lézerfény lineárisan polarizált. A lézerrudakat 1 cm átmérőben és 10 cm hosszúságban jó minőségben lehet előállítani Czochralski-féle kristálynövesztéssel. Az alexandrit lézerek három és négynívós rendszerben is működtethetőek. A háromnívós működési mód a rubinlézer működéséhez hasonló: a lézer fix 680,4 nm-en emittál, és a lézerátmenet a 2E gerjesztett állapot és a 4A2 alapállapot között jön létre. Négynívós üzemmódban az alexandrit lézer széles sávban (700 nm-818 nm) hangolható. A pumpálás közvetlenül a lézerátmenet felső 4T2, spektrálisan kiszélesedett energianívójának populációját növeli. Ennek a sávnak az élettartama csupán 6,6 μs, ezért egy gyors sugárzásmentes átmenet során a hosszú élettartamú (1.54 ms) 2E nívó populációja kezd el növekedni. A két nívó nagyon közel (800 cm-1) van egymáshoz, így a szoros csatolásuk miatt a betöltöttségük Boltzmann eloszlást mutat. Szobahőmérsékleten ez pl. 60 %/40 %-os populáció arányt jelent. A 2E nívó hosszú élettartama miatt pufferként működik, és biztosítja a 4T2 felső nívón a populáció inverziót. A hőmérséklet emelésével a 4T2 nívó betöltöttsége tovább növelhető. A hőmérséklet növelése azonban az alsó lézernívó betöltöttségét is megnöveli. Ezen két, ellentétes folyamat együttesen határozza meg a kialakuló lézerátmenetet és korlátozza a hangolhatósági tartományt. A gyakorlatban a kristály hőmérsékletét tipikusan 30ºC és 300ºC között változtatják.
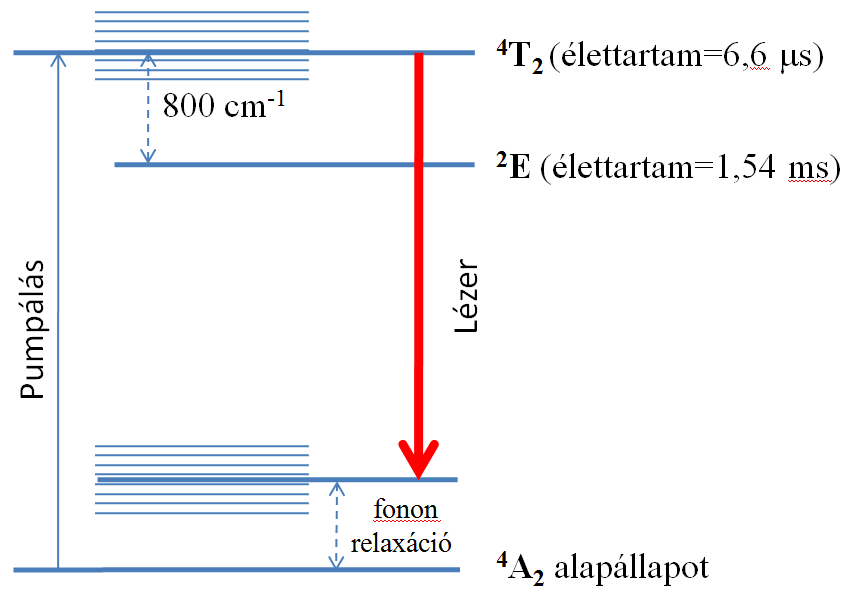
8.6. ábra. Az Cr3+:BeAl2O4 alexandrit lézer működésének energianívó vázlata.
A Ti:zafír lézer aktív anyaga a titánnal szennyezett Al2O3 kristály. A titán átmeneti fém, amelynek elektronszerkezete: Ti:...3d24s2. Trivalens állapotban a 3d pályán egy elektronja marad (Ti3+:...3d), ami a kristállyal kölcsönhatásban a 8.7. ábrán látható szélessávú energianívós szerkezetet hozza létre. A szennyezett kristály abszorpciós és fluoreszencia spektruma is széles, csúcsai 500 nm és 780 nm környékén helyezkednek el, ezért frekvenciakétszerezett Nd:YAG vagy Ar-ion lézerrel lehet gerjeszteni. A 2T2 alapállapot betöltöttsége a Boltzmann eloszlást követi, azaz tipikusan a felsőbb energianívók betöltetlenek. A pumpálás hatására a 2E gerjesztett állapot populációja megnő, de a gyors, sávon belüli sugárzásmentes átmenetek miatt a sáv legalsó energiaszintjéről történik a lézerátmenet a 2T2 sáv egyik belső nívójára. A foton emissziója után újra egy gyors, sávon belüli relaxáció történik. A Ti3+:Al2O3 kristály kitűnő hővezetési, mechanikai tulajdonságokkal rendelkezik, 3,5 cm átmérő és 15 cm hosszúságban hagyományos Czochralski-féle kristálynövesztéses módszerrel állítható elő. A hagyományos Ti:zafír lézerek széles sávban hangolhatók, a legnagyobb hatásfokkal a 700 nm-900 nm tartományban. A hangoláshoz általában kettősen törő szűrőt alkalmaznak, de a szélesebb hullámhossztartomány eléréséhez a lézer rezonátortükreinek a cseréje is szükséges. A széles erősítési görbe miatt a Ti:zafír lézerek különösen alkalmasak rövid impulzusú lézerek előállítására.
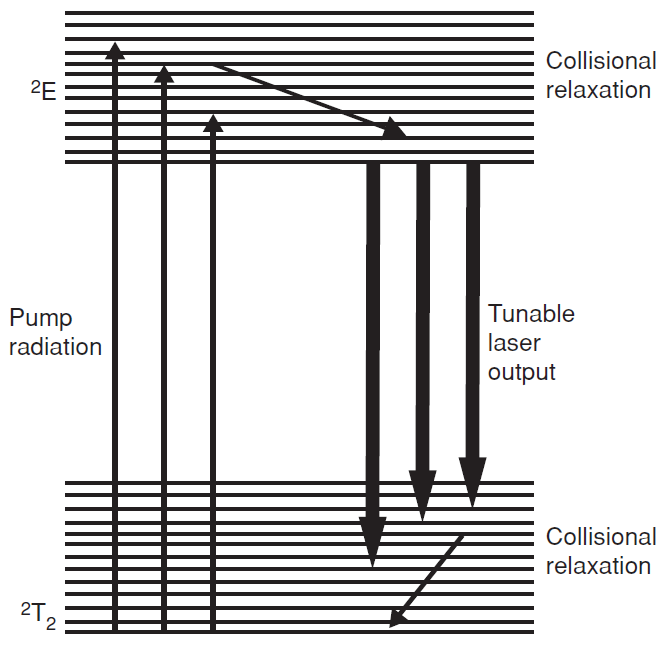
8.7. ábra. A Ti:zafír lézer energianívó vázlata. [8.1]
Mi az oka, hogy a rubinlézerek elsősorban impulzusüzemben működnek?
Miért nem változik a Nd lézerek hullámhossza a hordozóanyagtól függően?
Hasonlítsa össze az üveget és a kristályt, mint hordozóanyagokat, a lézer működése szempontjából fontos szempontok alapján!
Milyen hullámhosszakon működtethetők az Er lézerek? Ismertesse az Er:üveg lézerek gerjesztésének mechanizmusát!
Mi a hangolható szilárdtestlézerek működésének az alapja?
[8.1] W. Koechner: Solid-State Laser Engineering (Springer Series in Optical Sciences, 2006)
[8.2] http://en.wikipedia.org/wiki/Diode-pumped_solid-state_laser
[8.3] A. Yariv and P. Yen: Photonics (Oxford University Press, 2007)
[8.4] C. C. David: Lasers and Electro-Optics (Cambridge University Press, 1996)
[8.5] J. T. Verdeyen: Laser Electronics (Prentice Hall, 1981)
[8.6] J. C. Walling: Tunable Alexandrite Lasers (IEEE J. Quant. Electron. QE-16, 1302-1315, 1980)
[8.7] W. T. Silfvast: Laser Fundamentals (Cambridge University Press 2003)
Tartalom
A 2000. év Fizikai Nobel díját hárman kapták megosztva: Z.I. Alferov, H. Kroemer és J.C. Kilby. Az első két díjazott a nagysebességű optoelektronikában használatos félvezető heterostruktúrák kifejlesztéséért kapták az elismerést. Alferov és Kraemer egymástól függetlenül dolgozták ki azt a praktikus alkalmazásokat lehetővé tevő félvezető struktúrát, amely a mai félvezető lézerek alapjául is szolgál. (Csak érdekességként említjük, hogy az elmúlt évtizedek technikai forradalmának másik pilléréhez, a mikroelektronikához való hozzájárulást ismerték el abban az évben Jack Kilby kitüntetésével, az első integrált áramkör kifejlesztéséért.)
Noha a félvezető lézerek sok lézertípust megelőzve az elsők között demonstrálták az indukált emisszión alapuló koherens fényforrások megvalósíthatóságát, széles körű elterjedésükhöz évtizedeket kellett várni. A kettős heterostruktúrák alkalmazása a hatvanas évek második felében lehetővé tette a töltéshordozók és a fotonok együtt tartását, térbeli korlátozását (confinement), így szobahőmérsékleten is megvalósíthatóvá vált a folytonos üzemű működés (cw). Fontos technológiai fejlesztések valósultak meg, melyek lehetővé tették a különböző összetételű félvezetők együttes felhasználását, a növesztési, megmunkálási technikák finomodásával a félvezető lézerek hosszú várható élettartamú, megbízható, hatékony eszközökként foglalták el helyüket a hétköznapi alkalmazásokban. Az alacsony veszteségű, nagytávolságú kommunikációban használható optikai szálak megjelenése segített kihasználni a félvezető lézerek természetes előnyeit: a kimenet közvetlen modulálásának lehetőségét és az elektronikával való természetes integrálhatóságát.
A félvezető lézerek előnyös tulajdonságai a következők:
egyszerű elektromos gerjesztés
a gerjesztő áram változtatásával a kimenet modulálható
magas, akár 50%-ot meghaladó energia átalakítási hatásfok
robusztus, megbízható kivitel
kis méretek, tipikus beépítési sűrűség >1000/cm2
tömeges mennyiségben automatizáltan előállíthatók
számos paramétere az alkalmazások igényeinek megfelelően optimalizálható
A lézerműködéshez több feltétel egyidejű teljesülése szükséges. A legfontosabb feltétel, hogy valamely folyamat fénykibocsájtással járjon. A félvezető átmenetekben az elektronok és lyukak rekombinációja az a folyamat, amely fénykibocsájtással járhat. Egy p és egy n típusú szennyezésű félvezető egymáshoz illesztésével (külső feszültség alkalmazása nélkül) a töltéshordozók diffúziója megindul, ám a határrétegben a rekombinációk egy potenciálgátat alakítanak ki, amely megakadályozza a további töltéshordozók behatolását a másik szennyezéssel rendelkező rétegbe. Nyitóirányú feszültséget alkalmazva (az n szennyezettségű félvezető a negatívabb) az átmeneten folyamatos a töltéshordozók áramlása. Bizonyos félvezetők esetében ilyenkor az elektron többletenergiája a rekombináció során foton kibocsájtásával jár. A rekombináció mikéntje szerint a félvezetők két csoportba sorolhatók: a direkt és az indirekt sávú (sávátmenetű) csoportokba. (Az osztályozás nem minden esetben éles: a GaAs például direkt sávú, míg a GaP indirekt, de a GaAs-hez kis mennyiségű foszfort adalékolva a félvezető továbbra is direkt sávú marad, amíg a foszfor adalékolás mértéke egy küszöb alatt marad) A rekombináció során a direkt átmenetű félvezetőkben a vegyértéksáv energiamaximuma és a vezetési sáv energiaminimuma a töltéshordozók ugyanazon impulzusánál van, így a rekombináció közvetlenül megvalósulhat. A sávszerkezeteket sematikusan ábrázolja az 9.1. ábra.
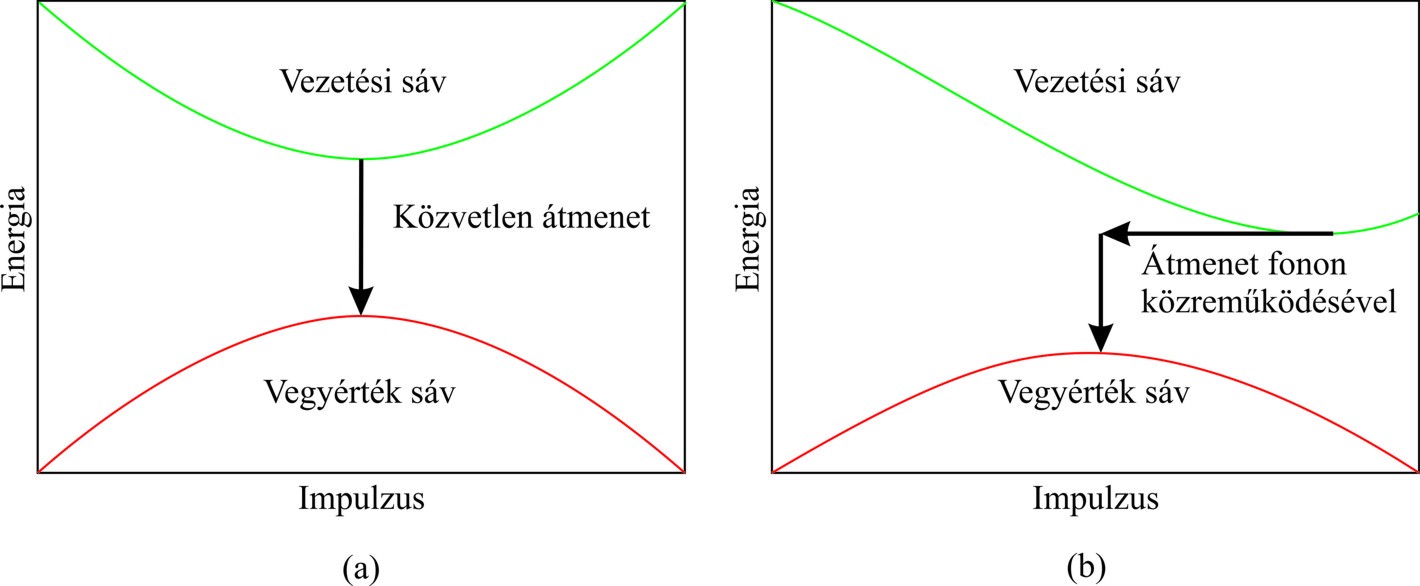
9.1. ábra. Direkt (a) és indirekt (b) sávátmenetű félvezetők sematikus sávszerkezete.
Az indirekt sávátmenetű félvezetőkben a rekombinációhoz általában egy fonon közreműködése is szükséges, mivel a rekombináció során kibocsájtott foton impulzusa elhanyagolható az elektron és lyuk impulzusának különbsége mellett, az impulzus megmaradást a fonon részvétele biztosítja. Mivel az elektronikában széles körben alkalmazott szilícium indirekt sávátmenetű, az ebből készített diódák sem LED-ként, sem dióda lézerként nem működnek. Az első táblázatban a legfontosabb direkt átmenetű félvezetőket soroltuk fel működési hullámhosszukkal.
|
Aktív anyag/szubsztrát |
Működési hullámhossz (nm) |
|---|---|
|
InGaN/GaN |
360-525 |
|
SiC |
470 |
|
GaP |
550-590 |
|
GaAs0.15P0.85 |
589 |
|
AlGaInP/GaAs |
625-700 |
|
GaAs0.35P0.65/GaAs |
632 |
|
GaAs0.6P0.4/GaAs |
650 |
|
GaAsP/GaAs |
700 |
|
Ga1-xAlxAs/GaAs |
650-900 |
|
GaAs |
910-1020 |
|
InGaAsP/InP |
600-1600 |
1. táblázat. A legfontosabb inorganikus félvezetők
A félvezető lézerek között a legelterjedtebbek az úgynevezett vegyület félvezetők (compound semiconductors), amelyek több kémiai elemből állnak. A bináris vegyület févezetők két, a ternáris és kvaternáris három és négy elem kompozíciójaként állíthatóak elő. A bináris vegyület félvezetők általában a periódusos rendszer IIIa és Va csoportjából tartalmaznak komponenseket a két elem azonos arányú kompozíciójaként. A lehetséges alkotóelemek közül a IIIa csoportba az alumínium (Al), a gallium (Ga) és az indium (In) tartozik, míg az Va csoportba a nitrogén (N), a foszfor (P), az arzén (As) és az antimon (Sb). A felsorolt anyagok jellemzői, mint az energiaszintjei, tiltott sávszélessége, rácsállandója, törésmutatója fogják a vegyület félvezetők tulajdonságait meghatározni. A ternáris félvezetők úgy származnak a binárisokból, hogy a megfelelő csoportokból származó anyagok helyettesítik valamely összetevőjének egy részét úgy, hogy a két nevezett csoportból származó anyagok továbbra is egyenlő arányban szerepeljenek a kompozícióban. Példaként említsük meg a GaAlAs-et, ahol az alumínium hozzákeverése megnöveli a tiltott sáv szélességét (Ez természetesen rövidebb működési hullámhosszat eredményez.). A lehetséges kompozíciót összefoglalhatjuk a következő módon: Ga1-xAlxAs, ahol x 0 és 1 közötti érték. További komponens hozzáadásával további tervezési szabadság kapható, az újabb komponens hozzáadásával továbbra is a két csoportból származó anyagok egyenlő arányát kell fenntartani. Példaként említhetjük az In1-xGaxAs1-yPy összetételt, ahol x és y egyaránt 0 és 1 közötti szám. Ezzel egy kvaternáris (négy összetevőjű) vegyület félvezetőhöz jutottunk. A IIIa-Va rendszerhez hasonló rendszereket építhetünk a II. és VI., illetve két IV. csoportba tartozó komponens felhasználásával. A 2. ábrán látható a különböző vegyület félvezetőkkel elérhető hullámhossz tartományok.

9.2. ábra. A legfontosabb vegyület félvezető lézerek működési hullámhosszai.
A kilencvenes évek nagy áttörése volt a kék félvezető lézerek megvalósítása, amelyek a GaInN kompozíción alapulnak. Amint a 2. ábrán látható, alumínium hozzáadásával mélyen az UV tartományba juthatnánk, valójában 340 nm-es hullámhosszig állítanak elő lézereket, és 270 nm-ig LED-et. A rövidebb hullámhosszakat az akadályozza, hogy a növekvő alumínium tartalommal egyre nehezebb az áramvezető kontaktusok megvalósítása. A GaN típusú anyagok legfontosabb alkalmazása az optikai adattárolás (DVD, Blu-ray).
A félvezető dióda lézerek mára az elektromágneses spektrum minden tartományán kínálnak megoldásokat. Ebben nagy szerepe van a vegyület félvezetőknek. Ugyanakkor a működési hullámhossz szabad megválaszthatóságának ára van: a különböző anyagi tulajdonságok kompatibilitására is tekintettel lenni. A hővezetés és a hőtágulás az a két legfontosabb tulajdonság, amely a már korábban említetteken túl szerepet játszik. Két fontos jellemzőt, a tiltott sáv szélességét és a rácsállandót ábrázolja a 9.3. ábra, különböző kompozíciójú félvezetők esetén.
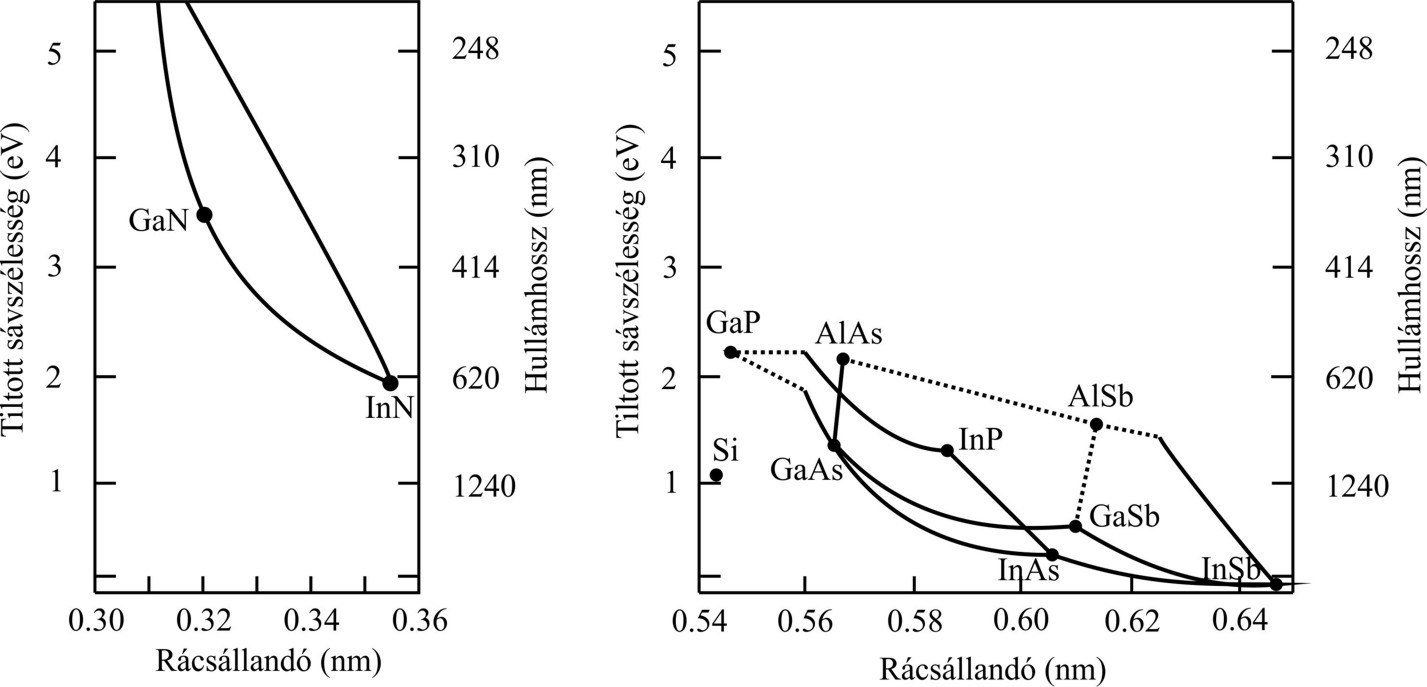
9.3. ábra. A III - V csoportba tartozó legfontosabb vegyület félvezetők rácsállandójának és tiltott sávszélességének függése az összetételtől.
Az ábrán a szaggatott vonalak mentén szereplő összetételek indirekt sávúak, így ezek általában lézerek aktív anyagaként nem használhatóak. A félvezető lézerek általában több rétegből állnak, amely rétegek fontos szerepet játszanak a működésben. Az egymással érintkező rétegek különböző tiltott sávszélessége nem zavaró, azonban a rácsállandóknak közeli értékkel kell rendelkezniük, mert a rácshibák lerontják a működést. Ebből következően a félvezető lézerek rétegeit alkotó kompozícióknak a 3. ábrán közel egy függőleges egyenesre kell esniük. A félvezető lézereket általában olyan hordozóra (substrate) növesztik, amely könnyen előállítható kétkomponensű anyag, mint az InP vagy a GaAs.
Az első félvezető lézerek két azonos komponensű rétegből álltak (általában GaAs), az egyiket donor, míg a másikat akceptor típusú anyaggal szennyezték. Az n-típusú és p-típusú rétegek összeillesztésével alakult ki az a határréteg, amelyben a nyitóirányú előfeszítés hatására nagyszámú rekombináció során keletkezett fény. Az ilyen szerkezeteket homostruktúrának nevezték el, ami az azonos anyagú (noha különböző szennyezettségű) rétegszerkezetre utalt. A homostruktúrájú dióda lézerek igen rossz hatásfokkal működtek, mivel sem a töltéshordozók, sem a keletkező fény szétterjedését nem korlátozta térben semmi, így a kritikus populáció inverziót csak nagy gerjesztő árammal lehetett elérni. A veszteségek hő formájában jelentek meg a határrétegben, ezért ezek a lézerek csak kriogenikus körülmények között, és csak impulzus üzemmódban működtek.
A heterostruktúrák alkalmazása - amelyben általában három különböző anyagi összetételű félvezető alkotja a lézerdiódát - azon alapul, hogy az n és p szennyezettségű rétegek képesek a töltéshordozók és a fotonok szétterjedésének megakadályozását. A donor és akceptor rétegeket nagyobb tiltott sávszélességű anyagból alkotják, ezzel elérve, hogy az aktív közegként szereplő (általában szennyezetlen) rétegre korlátozódik a rekombináció. A háromrétegű heterostruktúra rétegjeinek energiasávjait ábrázolja a 9.4. ábra
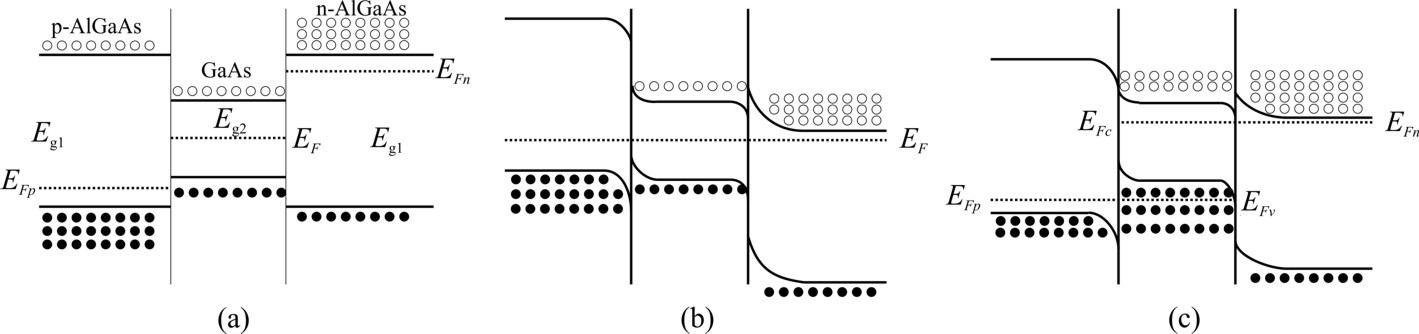
9.4. ábra. GaAs alapú heterostruktúra sávszerkezete (a) a rétegek összeérintése nélkül, (b) a rétegek összeérintése után, de feszültség alkalmazása nélkül, (c) nyitóirányú feszültség alkalmazásával
Az (a) ábra azt a helyzetet ábrázolja, amikor a három réteg még nincs kontaktusban egymással, míg a (b) ábra a kontaktusban lévőket. Ebben az esetben a három réteg Fermi szintje megegyezik. A vegyérték sávon a bal oldalon, míg a vezetési sávon a jobb oldalon ábrázoltuk a többségi töltéshordozók diffúzióját követő rekombináció során kialakult potenciálgátakat, amelyek a további rekombinációt gátolják. A (c) ábra a nyitóirányú feszültség hatására kialakult viszonyokat ábrázolja. Az alkalmazott feszültség hatására megjelennek az n és p szennyezettségű rétegek kvázi Fermi szintjei, illetve az alkalmazott feszültség lehetővé teszi a többségi töltéshordozók behatolását a határrétegbe, megindítva a rekombinációt.
Az aktív réteget két oldalról határoló szennyezett rétegek törésmutatóját úgy választják meg, hogy az nagyobb legyen az aktív rétegénél, így azok hullámvezetőként működnek a rekombináció során keletkező fotonok számára.
A félvezető dióda lézerek optikai jellemzői, mint az abszorpció illetve erősítési tényező egy adott hullámhosszon meghatározható a fénykibocsátásért felelős részecskék statisztikus tulajdonságaiból. Egy atomi rendszerben ehhez a különböző gerjesztettségű részecskék számát, statisztikai súlyát és az átmenet spektroszkópiai jellemzőit, mint élettartamok és vonalalakok kell ismernünk. A félvezető dióda lézerek esetében viszont az egymással kölcsönhatásban álló elektrongáz, illetve a félvezető kristály által együttesen meghatározott sávszerkezet szolgál a számolás alapjául.
A félvezetőkben az elektronok a következő hullámfüggvénnyel írható le:
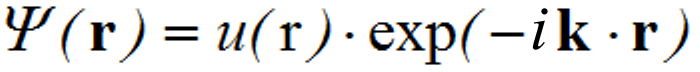 |
. | (9.1) |
Tegyük fel, hogy a kristály Lx, Ly és Lz méretekkel rendelkezik, ekkor k komponenseire a következő feltételeknek kell teljesülnie:
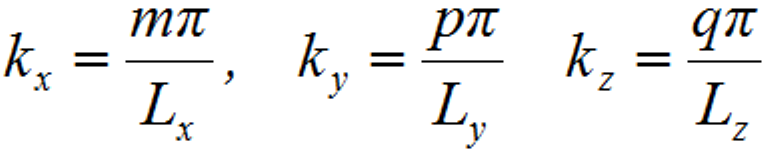 |
. | (9.2) |
A fenti jelölésekkel, illetve annak figyelembe vételével, hogy elektronokról van szó a k és a k+dk tartományban a ρk állapotsűrűség a következő:
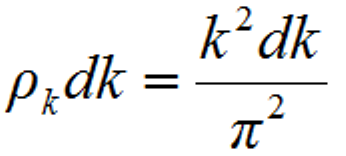 |
. | (9.3) |
Kihasználva E és k kapcsolatát
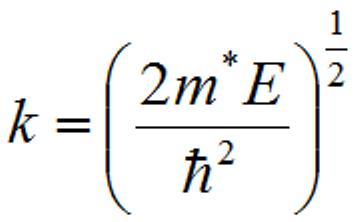 |
, | (9.4) |
(ahol m* az elektron (lyuk) effektív tömege, E az energiája a megfelelő sáv éltől mérve) kifejezhetjük az állapot sűrűséget az energia függvényében is:
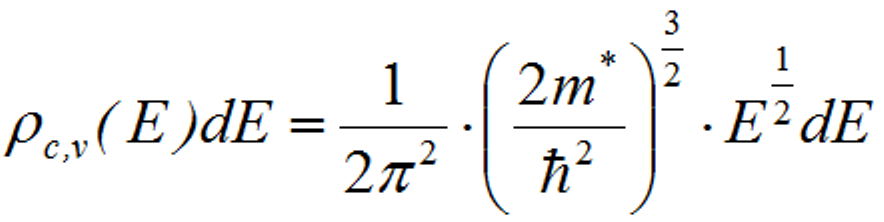 |
. | (9.5) |
Az állapot sűrűség önmagában csak 0 K hőmérsékletű kristály esetén hordoz információt az állapotok betöltöttségéről is, hiszen ebben a speciális esetben a Fermi szintig minden állapot betöltött, míg a fölött mindegyik állapot üres. Minden más esetben figyelembe kell vennünk az egyes állapotok betöltöttségének valószínűségét is. A T hőmérsékletű EF Fermi energiájú elektrongázban az
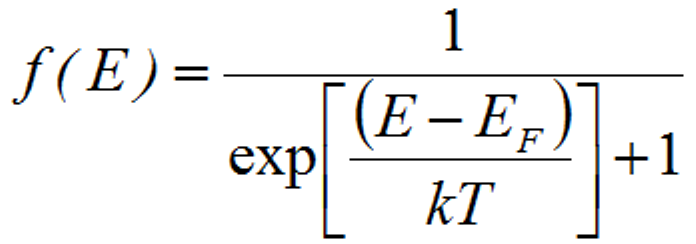 |
(9.6) |
függvény adja meg, amennyiben az E energiaállapot lehetséges. A fenti betöltési valószínűség egyensúlyi állapotban érvényes, ez azonban nem áll fenn egy olyan közegben, amelyben populáció inverziót hozunk létre. A továbblépés a W. Shockley által javasolt "kvázi Fermi szint" koncepciója. Ez röviden azt fejezi ki, hogy a sávon belüli relaxációk nagyságrendekkel gyorsabban valósulnak meg, mint a sávok közötti rekombináció, így (9.6) egyenlethez hasonló kifejezések írhatóak fel külön a lyukak, illetve elektronok lehetséges energiaállapotainak betöltöttségére, ahol az egyes sávok saját Fermi szinttel (Fn és Fp) jellemezhetőek. Ezek figyelembe vételével a vezetési (vegyérték) sávban az elektronok (lyukak) számára az E és E+dE tartományban a következő összefüggést kapjuk:
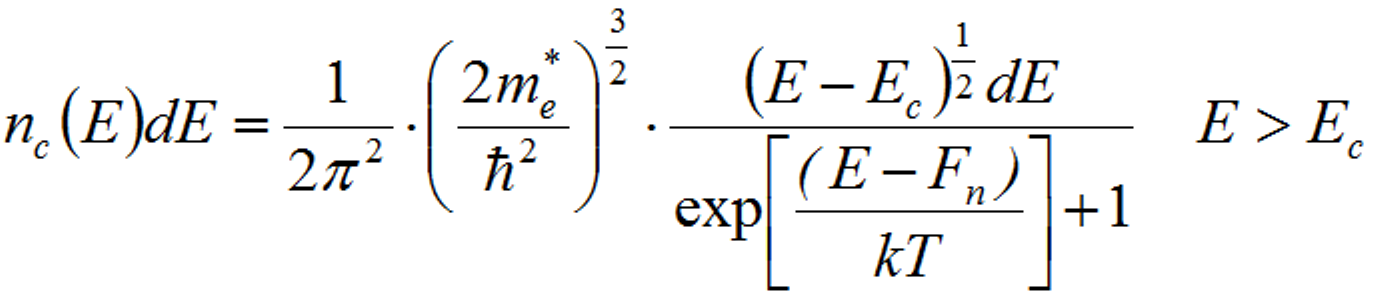 |
, | (9.7) |
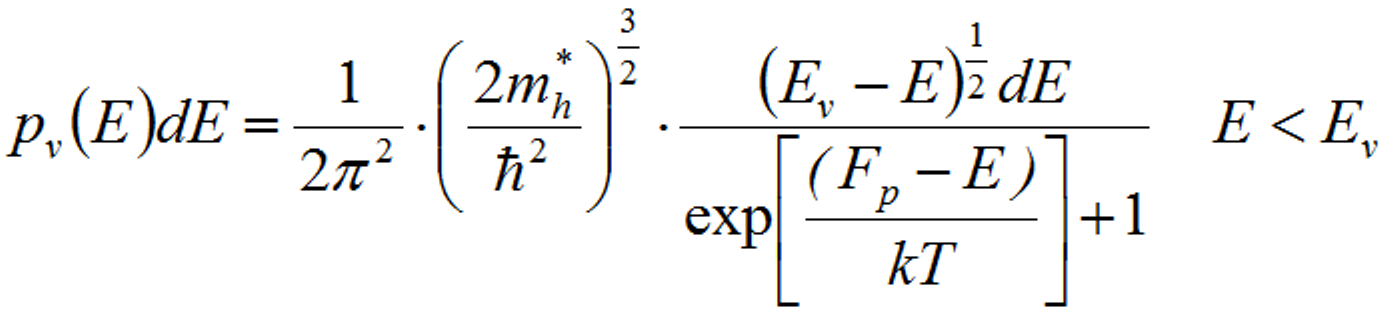 |
. | (9.8) |
A fenti összefüggésekben Ec (Ev) a vezetési sáv alsó (a vegyérték sáv felső) élének energiája, Fn (Fp) a vezetési (vegyérték) sáv kvázi Fermi szintje. Az elektronok és lyukak állapotainak betöltöttsége alapjául szolgálhat a populáció inverzió létrejöttének elemzéséhez. Hosszadalmas számolások mellőzésével csak megállapítjuk, hogy az inverzió feltétele a következő:
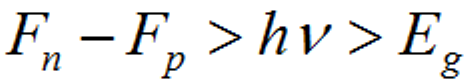 |
. | (9.9) |
A kisjelű erősítési tényező meghatározását megkönnyíti a redukált (közös) állapot sűrűség (ρjnt) bevezetése, amely az eddigieken túl az impulzus megmaradását várja el azáltal, hogy az átmenet során k nem változhat, az átmenet során keletkező foton impulzusa ugyanis elhanyagolható a vezetési sávban lévő elektron és a vegyértéksávban lévő lyuk impulzusához képest.
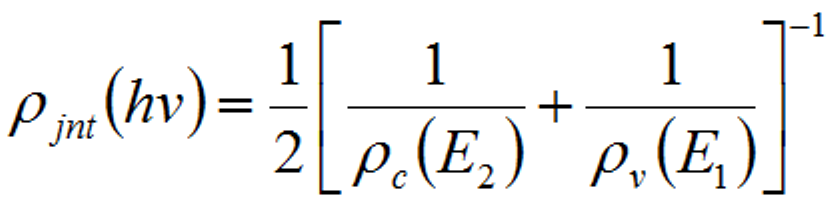 |
. | (9.10) |
A figyelembe vett optikai folyamatok, az abszorpció és indukált emisszió sebessége a következő módon írható fel:
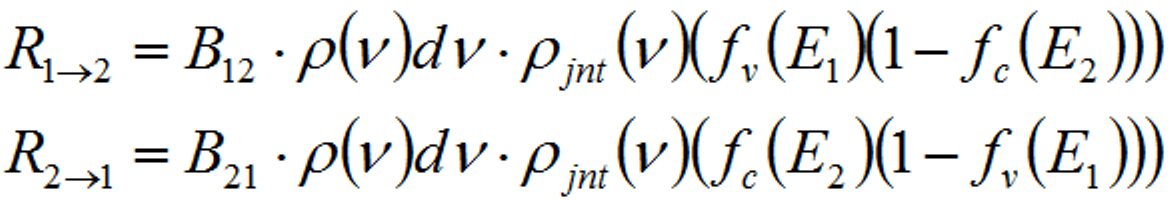 |
, | (9.11) |
ahol B12 és B21 a megfelelő Einstein koefficiensek, ρ(ν)dν pedig a ν és ν+dν frekvenciatartományba eső fotonok száma. A kisjelű erősítési tényező ezek alapján a következőképpen adható meg:
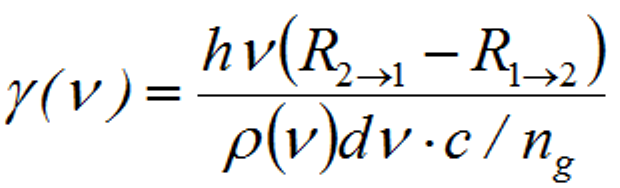 |
, | (9.12) |
ahol ng a csoport törésmutató és c a fénysebesség. Minden behelyettesítést elvégezve a kisjelű erősítés:
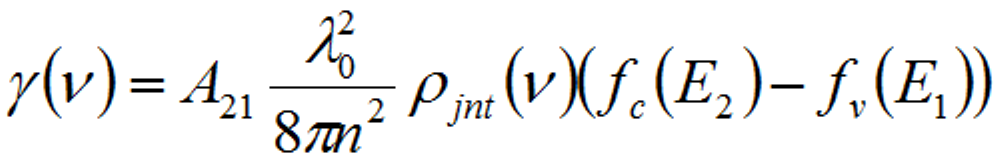 |
. | (9.13) |
A kisjelű erősítés (9.13) alakjának részleteit ábrázolja az 9.5. ábra.
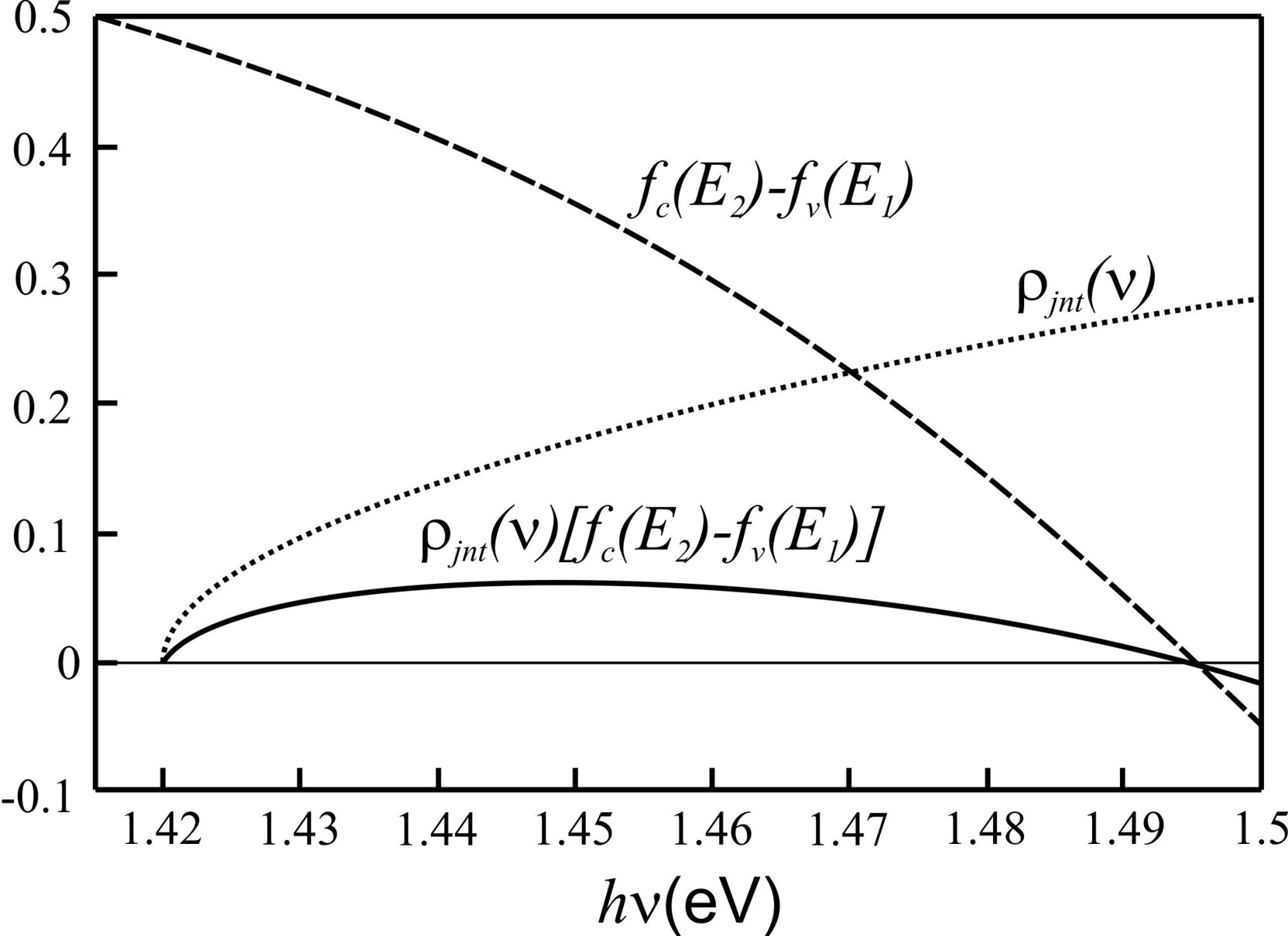
9.5. ábra. A redukált (közös) állapotsűrűség (ρjnt), a vezetési és vegyértéksáv betöltöttségének különbsége ( f c(E2) - f v(E1) ), valamint szorzatuk a foton energia (hν) függvényében.
Mint látható, a kisjelű erősítési tényező egy monoton növekvő és egy monoton csökkenő függvény szorzataként áll elő. A töltéshordozók számának növelése ennek következtében nem csupán a kisjelű erősítési tényező (egyébként közel lineáris) növekedéséhez vezet, hanem az erősítési profil maximumának a nagyobb foton energia felé való eltolódásával is jár. A 6. ábrán GaAs esetén ábrázoltuk növekvő töltéshordozó koncentráció esetén a kisjelű erősítési tényező hullámhossz függését. Mint látható, a töltéshordozó koncentráció jelentősen befolyásolja a kisjelű erősítési tényezőt: a lézerműködés küszöbáramát meghaladva a kisjelű erősítési tényező gyorsan nő, és akár a 100 cm-1 értéket is meghaladhatja, valamint maximuma eltolódik a rövid hullámhosszak felé.
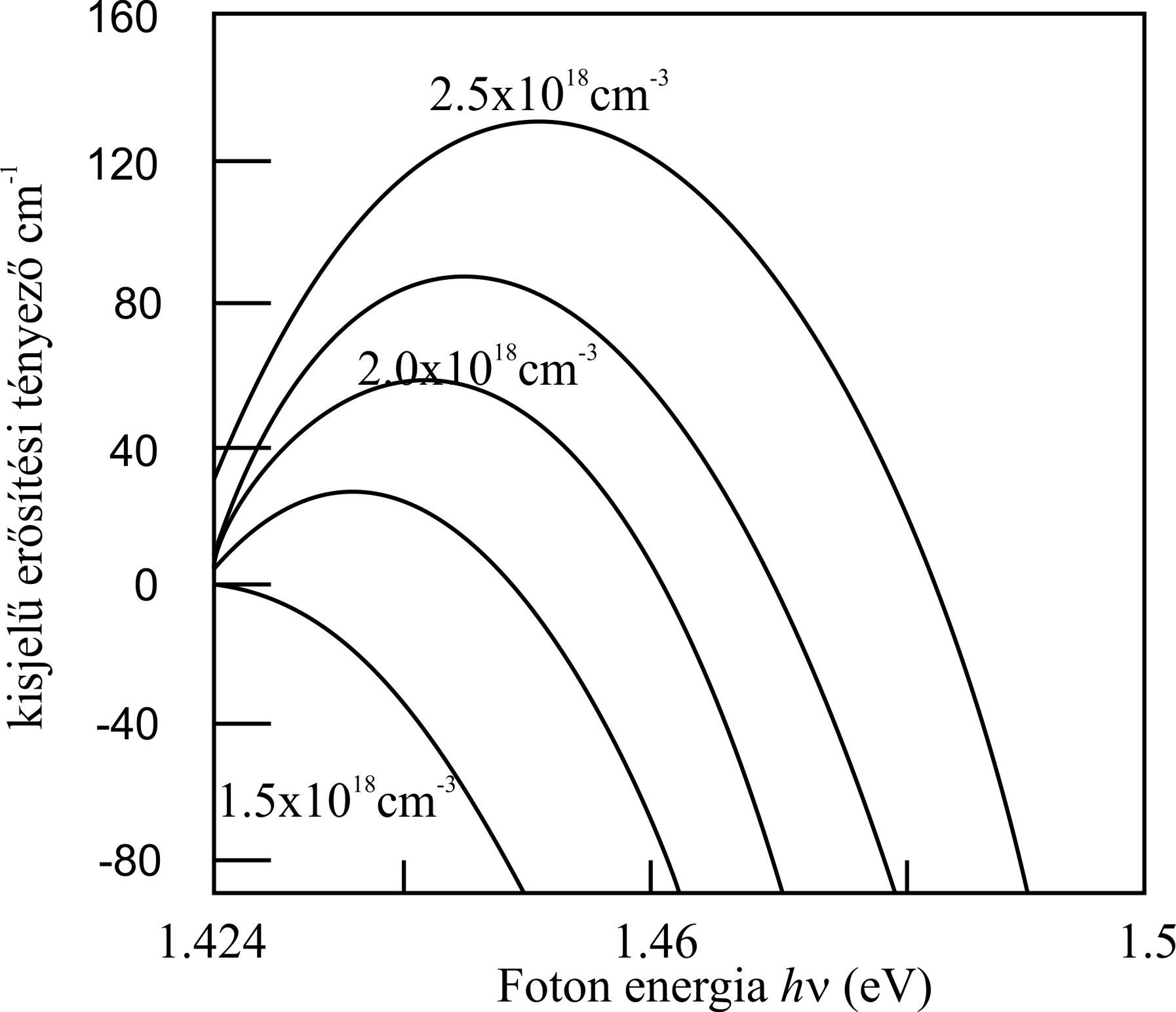
9.6. ábra. A GaAs lézerdióda kisjelű erősítésének hullámhossz függése különböző gerjesztő áramok esetén.
Ez az effektus különösen fontos lehet azoknál az alkalmazásoknál, amelyben félvezető dióda lézert alkalmaznak szilárdtest lézer gerjesztéséhez. Amennyiben a szilárdtest éles abszorpciós sávval rendelkezik, a fent említett effektus a gerjesztő lézer intenzitásának növelésekor elhangolódhat az abszorpciós sávtól, lerontva a gerjesztés hatásfokát.
A dióda lézerek rezonátorát sokféleképpen kialakíthatják. A legkézenfekvőbb csoportosítást az aktív réteg és a rezonátor irányának viszonya alapján tehetjük meg. A dióda lézerek rezonátorát sokáig úgy építették, hogy az aktív réteg két párhuzamos síkját hasítással (cleavage) tükörré alakították, míg az oldalsó határoló felületeit érdesítették. (A hasítással kialakított felületek annak következtében képesek igen jó minőségű tükörként működni, hogy a félvezető kristályok bizonyos kristálytani irányban igen könnyen hasíthatóak.) Az ilyen eszközöket hívjuk élsugárzó lézereknek, mivel ilyenkor a rétegszerkezet oldalán lép ki a lézerfény. Az ilyen elrendezés legfőbb előnye, hogy a szerkezet teljes hosszából (ez tipikusan néhány száz μm) kinyerhető az energia, ez nagy kimenő teljesítményt eredményezhet.
Alternatív megoldás, amikor az aktív rétegre merőleges irányban lép ki a fény, ekkor a visszacsatoló elem síkja párhuzamos az aktív réteggel. Ennél a megoldásnál az aktív réteg vastagságával egyezik meg a rezonátorhossz (ez tipikusan a keltett fény hullámhossza nagyságrendű), és igen jó nyalábminőség érhető el ezzel a megoldással.
A rezonátor legegyszerűbb megvalósítása az, amikor a lineáris üreget az aktív, gerjesztett térrész alkotja és a síktükrök az aktív réteg határoló oldallapjai. Ugyan a tipikus félvezető lézer rezonátorok csak 300-500 μm hosszúak, a nagy erősítési tényező miatt így is elérik a milliwatt szintű átlagteljesítményt. A rezonátort alkotó tükröket a félvezető kristály felületei alkotják, ez minden különösebb bevonat nélkül lehetséges, mivel a félvezetők nagy törésmutatóval rendelkeznek. (A GaAs esetében ez 780 nm hullámhosszon 3,34, a Fresnel formula alapján ez nagyjából 30% visszacsatolást biztosít, amely elégséges visszacsatolás a lézer oszcillációhoz.) Gyakorlatiasabb megoldás, ha a zárótükör felületén mégis kialakítanak nagy reflexiójú réteget, biztosítva, hogy csak egy irányban legyen kimenet, míg a zárótükör oldalán valósítják meg azt a monitor fotodiódát, amely visszajelzést ad a tápegységnek a rétegek degradációja okozta teljesítményváltozásokról. Azokban a lézerekben, amelyekben a fénykibocsájtás mikrométer magasságú és szélességű és 100 μm hosszúságú csatornában történik, csak egy transzverzális módus működik. A szélesebb csatornával rendelkezők esetében több transzverzális módus is lehetséges, amely kedvezőtlenül befolyásolja a nyalábtulajdonságokat.
A Fabry-Perot rezonátorú dióda lézerek igen rövidek, így a longitudinális módusok távolsága igen nagy, tipikusan néhány tized nanométer. A nagy módustávolság miatt ezek a lézerek gyakran egy módusban sugároznak, mégis előfordul a módusugrás jelensége: a széles hullámhossz tartományon meglévő jelentős erősítés és a hőmérsékletfüggő törésmutató a kimenet modulációja esetén megváltoztathatja a működés hullámhosszát. A Fabry-Perot rezonátorú lézer a legolcsóbban megvalósítható, ugyanakkor a hullámhossz stabilitása nehezen biztosítható. A CD lejátszókban alkalmazott lézer diódák ezzel a rezonátorral működnek.
A nagysebességű adattovábbítás, amely a félvezető lézerek igen fontos alkalmazási területe, a Fabry-Perot rezonátorral elérhetőnél pontosabban definiált hullámhosszat igényel. Ez elérhető, ha a rezonátor frekvencia szelektív elemet tartalmaz. A legelterjedtebb megoldás az elosztott visszacsatolás (distributed feedback, DFB) alkalmazása. Az aktív réteg egyik felületén D periódushosszú diffrakciós rácsot alakítanak ki a, amely megvalósítja a hullámhossz szelektív visszacsatolást.
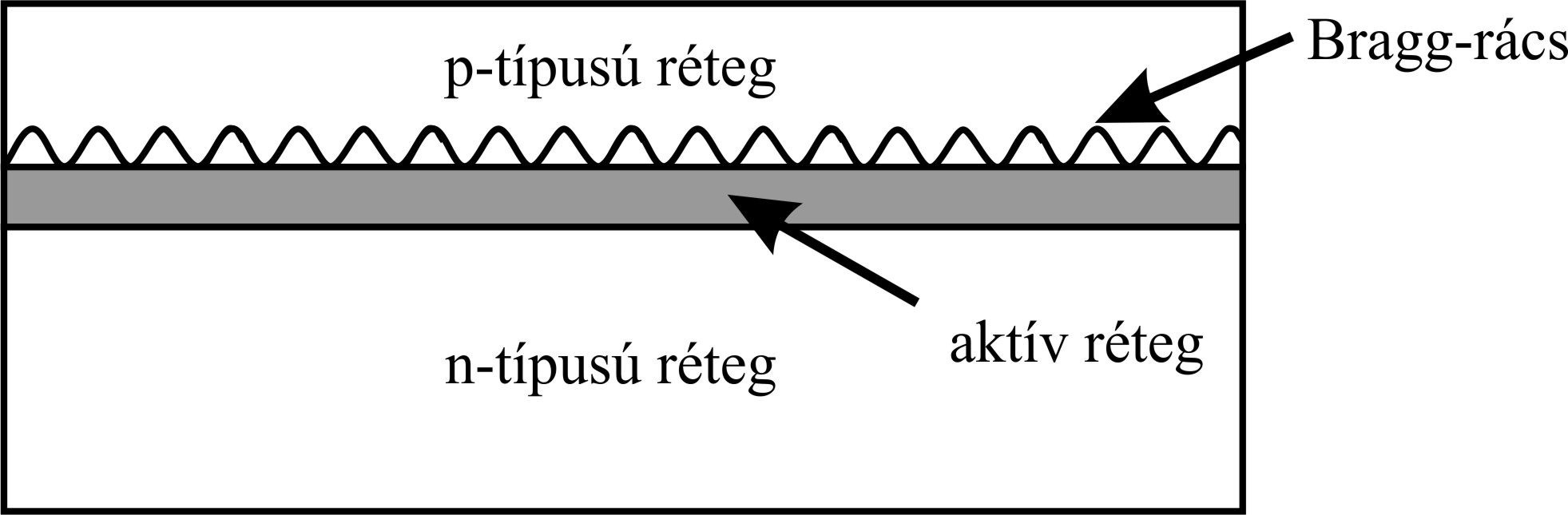
9.7. ábra. Elosztott visszacsatolású dióda lézer rezonátora, amelyben a kettős heterostruktúra egyik szennyezéses rétegén alakítják ki a visszacsatoló rácsot.
A D rácsperiódust, az n törésmutatót és a λ működési hullámhosszat a következő összefüggés kapcsolja össze:
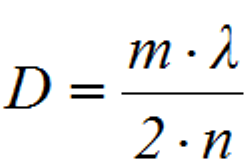 |
, | (9.14) |
ahol m egész szám. A GaAs λ = 1550 nm-es hullámhosszára, ahol az n = 3,4 törésmutató 228 nm-es, vagy 456 nm-es rácsperiódust jelent (m = 1, vagy m = 2 esetén). A működési hullámhossz továbbra is függ a hőmérséklettől (a törésmutató hőmérsékletfüggésén keresztül), de ez lényegesen kisebb mértékű hullámhossz változást eredményez, mint a módusugrás lehetőségével volt a Fabry-Perot rezonátor esetén. A visszacsatolást nem feltétlenül az erősítést tartalmazó réteg helyén kell megvalósítani: az erősítés nélküli részen elhelyezett diffrakciós rács ugyanazt a hatást fejti ki. Ezt a megoldást nevezik elosztott Bragg reflektornak, amelyet az 9.8. ábra mutatja.
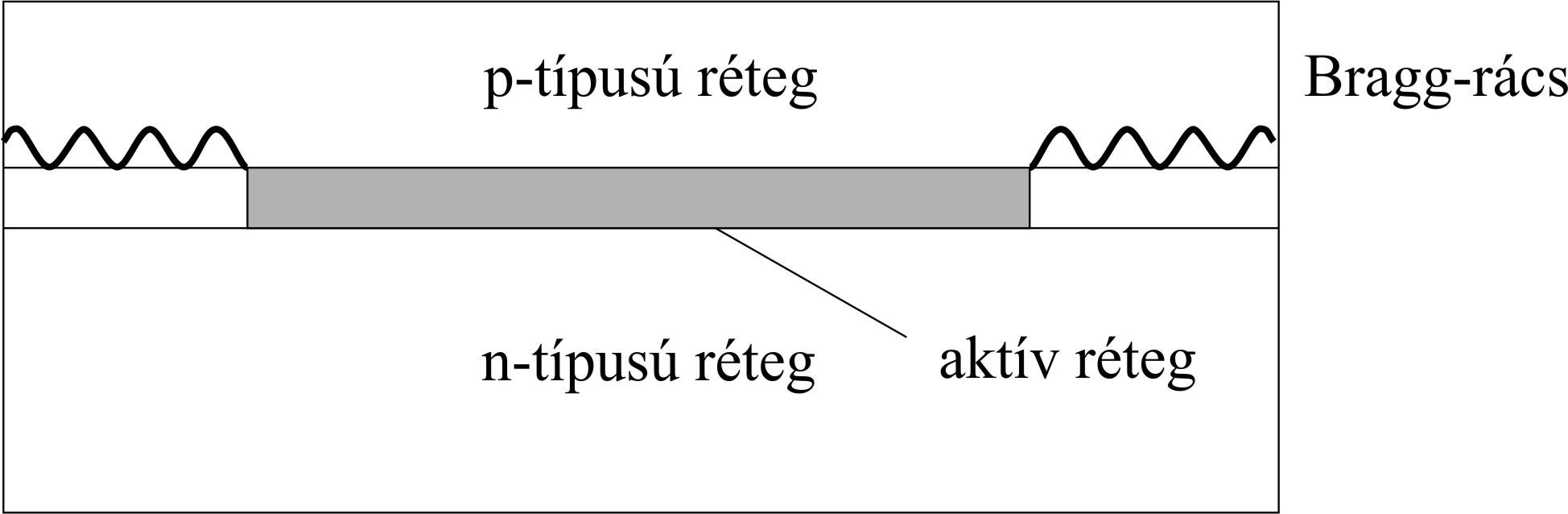
9.8. ábra. Elosztott Bragg reflektorral megvalósított visszacsatolású dióda lézer.
Ennek a megoldásnak egy továbbfejlesztett változata a "sample grating distributed Bragg reflector", ahol két Bragg reflektor és egy fázist szabályozó szakasz segítségével érik el a több tíz nm-es módusugrás nélküli hangolást. A különböző szerepet játszó rezonátor szakaszok általában önálló árambevezetéssel rendelkeznek, és a különböző mértékű gerjesztettséggel érik el a hangolást.
A rezonátor és az aktív réteg viszonya szerinti másik lehetséges megoldás, ahol az aktív rétegre merőlegesen építik fel a rezonátort. Az élsugárzó lézerek gyártása lényegesen bonyolultabb és költségesebb, mint a felületsugárzóké: az élsugárzók csak a félvezető szelet (wafer) feldarabolása után alakíthatóak ki, és tesztelésük is csak a tokozás után végezhető el (ez a legköltségesebb lépés a gyártás során). A felületsugárzók esetében a szükséges rétegek könnyebben valósíthatóak meg, a felületsugárzók könnyebben integrálhatóak összetett áramkörök monolitikus gyártásába. A felületsugárzók nagy felületű hengerszimmetrikus struktúrákból állnak, így optikailag könnyebben kezelhető nyalábokat állítanak elő az élsugárzóknál.
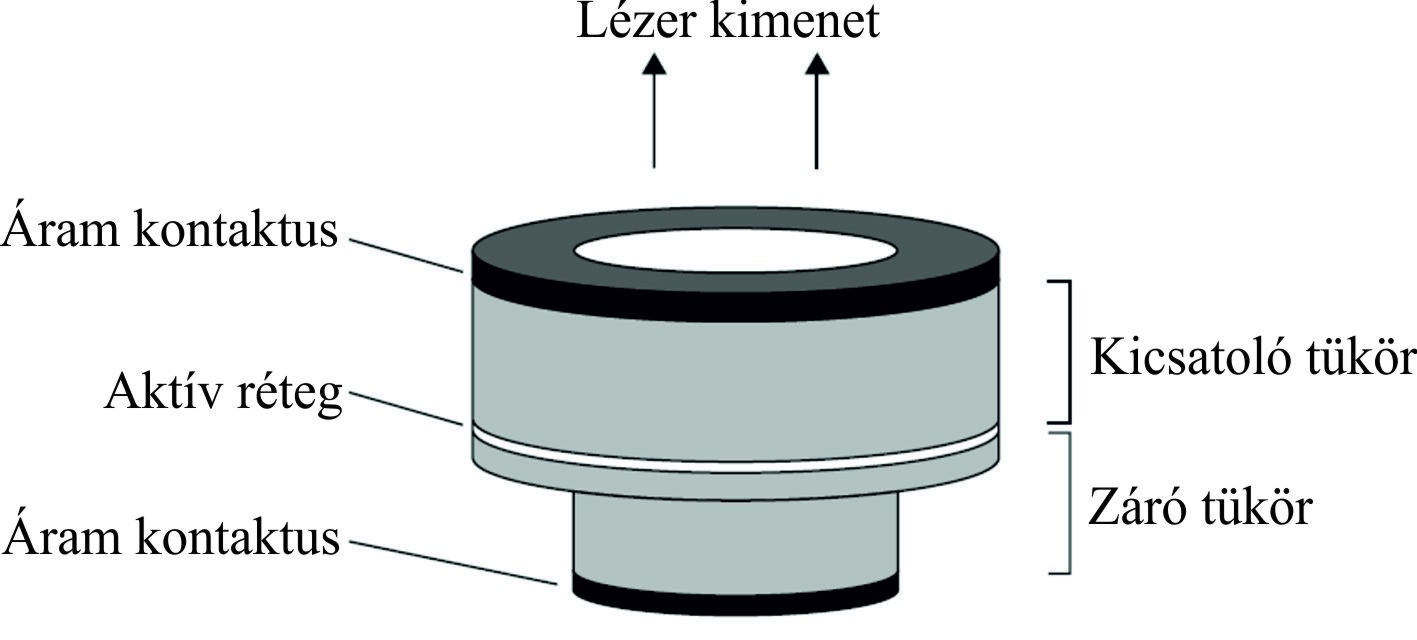
9.9. ábra. A vertikális üregű felületsugárzó lézer (VCSEL) szerkezete.
Az a tény, hogy ennél a geometriánál az aktív rétegre merőleges a rezonátor, több következménnyel jár. Noha a félvezetőkben igen nagy lehet a kisjelű erősítési tényező, az erősítés itt a rövid erősítési hossz miatt (az aktív réteg vastagsága a hullámhossz nagyságrendjébe esik) nagy jóságú rezonátort kell építeni, a kimenő teljesítmény így sem haladja meg a milliwattos szintet. Ez jelentősen elmarad az élsugárzókkal létrehozható teljesítmény szinttől. Ugyanakkor a rövid rezonátor miatt a longitudinális módusok távolsága már elegendően nagy ahhoz, hogy a módus ugrás jelensége ne tudjon fellépni ennél a konstrukciónál. A felületsugárzó lézerek hatásfoka ugyanakkor jelentősen meghaladja az élsugárzó lézerek hatásfokát, amely alacsony küszöbáramként jelentkezik, a felületsugárzó lézerek élettartama ebből következően sokkal hosszabb az élsugárzó lézereknél. A cirkuláris nyalábprofil megkönnyíti az optikai szálakba való becsatolást is. (A felületsugárzó lézerek tipikus nyalábkeresztmetszete 5 és 30 μm nagyságú.) A GaAlAs kompozíciójú felületsugárzókat gyakran használják rövid hatótávolságú kommunikációban, míg az InGaAsP összetételűekkel lehetséges az 1300 és 1550 nm-es hullámhosszú eszköz is, amely széles telekommunikációs alkalmazások lehetőségét hordozza.
A félvezető lézerek a bevezetőben említett előnyök következtében mára a legelterjedtebb lézerek között foglalnak helyet. Szerencsére a megismerésüket lehetővé tevő könyvek szép számban érhetőek el, amelyek közül néhányat az ajánlott irodalom listájában szerepeltettünk.
A jelen összefoglaló terjedelmi korlátai miatt néhány izgalmas területről egyáltalán nem esett szó. Elsőként kell megemlítenünk a kvantum kaszkád lézereket, amelyek a távoli infravörös spektrumon kínálnak nagyteljesítményű fényforrásokat. A működésük eltér a félvezető lézerekben bemutatottaktól annyiban, hogy nem a diódákban kialakuló határrétegben zajló rekombinációk eredményezik a fénykibocsájtást.
Szintén kimaradtak azok a félvezető lézerek, amelyekben a kölcsönhatási tartomány extrém szűkítésével valósíthatunk meg érdekes eszközöket: nem tárgyaljuk a kvantum zseb (quantum well), kvantum drót (quantum wire) és kvantum pötty (quantum dot) szerkezeteket, ezekben a félvezetők szokásos kvantummechanikai tárgyalásánál részletesebben kell figyelembe venni az aktív réteg elektron hullámhosszával összemérhető méreteit.
A gyakorlati alkalmazások számára fontosak lehetnek azok a megfontolások, amelyek a félvezető lézereket alkalmassá teszik arra, hogy szilárdtest lézereket gerjesszenek. A kialakítható tömbök számos mérnöki problémát tartalmaznak, így a részben koherens források térbeli elhelyezése, a gerjesztő árammal való ellátás lehetőségei, mindenekelőtt a termális problémák megoldása érdekes lehetett volna, de a terjedelem miatt ezek ismertetésére nem kerülhetett sor.
-
Mi egy dióda lézer legjobb aktív közege?
direkt sávátmenetű félvezető
indirekt sávátmenetű szigetelő
vezető
indirekt sávátmenetű félvezető
direkt sávátmenetű szigetelő
-
A következő anyagok között melyik kvarternális III-V félvezető?
GaAs
GaAlAs
InGaAsP
NSbAsP
PbSnSse
-
Mi teszi a kettős heteroszerkezetű lézert jobb hatásfokúvá a homoszerkezetű lézernél?
valójában a homoszerkezetű lézer a magasabb hatásfokú
a záróirányú előfeszítés
a vezetési elektronok jobb együtt-tartása
-
Melyik lézertípus készíthető GaAlAs felhasználásával?
Az elosztott visszacsatolású élsugárzó lézer
a VCSEL
Külső rezonátoros lézer
Fabry-Perot rezonátoros élsugárzó lézer
a fentiek mindegyike
-
Egy félvezető 1.5eV tiltott sávszélességgel rendelkezik. Milyen hullámhosszon fog lézerként működni?
333nm
667nm
1000nm
800nm
1500nm
[9.1] D. Sands: Diode Lasers (IOP Publishing Ltd, 2005, Bristol, Philadelphia, ISBN 0-7503-0726-9)
[9.2] E. Kapon (szerk): Semiconductor Lasers I-II, (Academic Press,San Diego, London, Boston, New York, Sidney, Tokyo, Toronto, 1999, ISBN 0-12-397631-6)
[9.3] W. Chow, S. Koch: Semiconductor-Laser Fundamentals (Springer Verlag, Berlin, Heidelberg, New York, 1999, ISBN 3-540-64166-1)
[9.4] K. Thyagarajan, A. Ghatak: Lasers - Fundamentals and Applications (Springer Verlag, New York, Dordrecht, Heidelberg, London, 2010, ISBN 978-1-4419-6441-0)
Tartalom
A fényvezetőszál-lézerek, röviden szál-lézerek [fiber lasers] a szilárdtest-lézerek egyik csoportját alkotják, ahol a fényerősítés egy fényvezető (optikai) szálban történik. A lézerműködésért felelős aktív anyag általában a fényvezető szálban lévő adalékanyag, leggyakrabban valamilyen ritkaföldfém, például erbium (Er) vagy itterbium (Yb). A lézerműködésen kívül más effektusok segítségével is lehetséges fényerősítés fényvezető szálakban. A fényvezető szál anyagában létrehozott kényszerített Raman-szóráson alapul a Raman szál-lézerek [Raman fiber lasers] működése. Gyakran a szál-lézerek közé sorolják a félvezető anyagú lézererősítőből (diódalézerből) és fényvezető szál alkotta rezonátorból álló lézereket is.
A szál-lézereket más szilárdtest-lézerektől elsősorban sajátos geometriájuk és az ebből eredő speciális tulajdonságaik különböztetik meg. Az 10.1. ábra különböző felépítésű szilárdtest-lézereket mutat. A hagyományos felépítésű lézereknél az aktív közeg jellemzően rúd alakú [rod laser], amelynek pumpálása oldalról vagy a véglapok felől történik (10.1.ábra (a) része). A lézerrúd hossza jellemzően 1 mm és 15 cm közé esik. A hűtés a köpenyen keresztül lehetséges, ezért a jellemzően 1 mm és akár több cm közé eső átmérő miatt ez kevéssé hatékony; a rúd keresztmetszete mentén hőmérsékleti gradiens alakul ki, amely gyakorlati szempontból kedvezőtlen. A viszonylag nagy átmérő megtartása mellett hatékony hűtést, és így nagy átlagteljesítményt, valamint jó nyalábprofilt tesz lehetővé a korong-lézer [thin-disk laser, vagy active-mirror laser] geometria (10.1. ábra (b) része). Mivel a korong vastagsága jellemzően a 100 µm-es nagyságrendbe esik, ezért a pumpa abszorpciója és a lézer erősítési faktor kicsi, amit csak viszonylag bonyolult, sok átmenetes nyalábvezetéssel lehet kompenzálni.
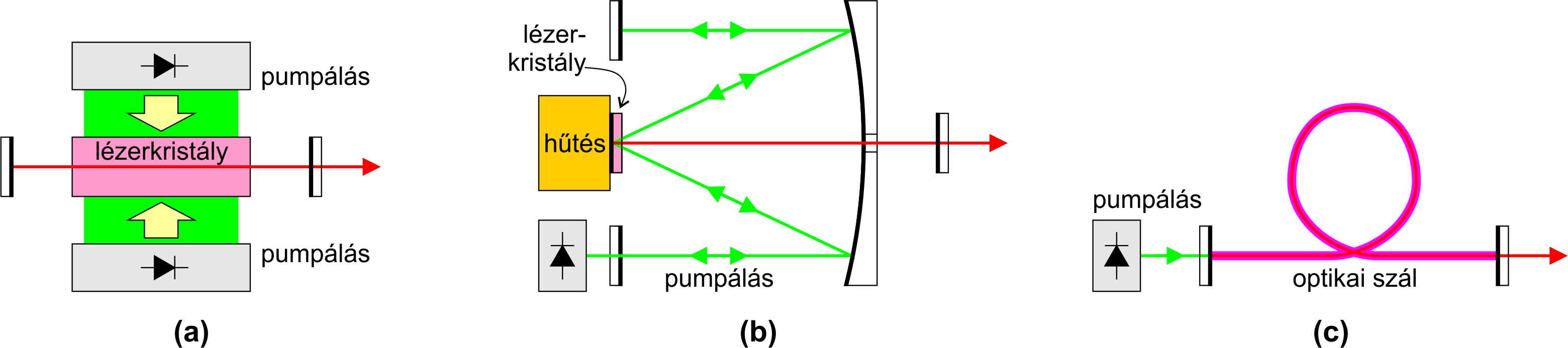
A szál-lézereknél az aktív közeg egy optikai szál (10.1. ábra (c) része), amelynek hossza jellemzően 10 cm-től akár néhány száz méterig, az átmérője pedig néhány µm-től a néhány száz µm-ig terjedhet. A rendkívül nagy abszorpciós és erősítési hossz miatt igen hatékony pumpálás és nagy erősítési faktor érhető el. A kis keresztmetszetnek köszönhetően a termikus effektusok többnyire elhanyagolhatók. A kis keresztmetszet és a nagy hossz miatt fellépő nemlineáris effektusok és az optikai roncsolódás azonban korlátozzák a kivehető teljesítményt. A különböző optikai elemek fényvezető szálba való integrálásával a levegőben való nyalábvezetés akár teljesen kiküszöbölhető és nagy stabilitású, megbízhatóan működő, kompakt lézerek építhetők.
A fényvezető szálban való lézererősítés elvének kidolgozása [10.1] és az első szál-lézer megépítése [10.2] Snitzer és munkatársai nevéhez fűződik, az 1960-as évek elején, nem sokkal az első lézer megépítése után. A szál-lézerek technológiája az 1980-as évek közepétől indult igazán gyors fejlődésnek. A fő hajtóerő az optikai kommunikáció volt, amelyet a diódalézerekkel való hatékony pumpálás és az 1,55 µm körüli hullámhosszon működő Er adalékolású szál-lézerek [10.3] megjelenése forradalmasított. A telekommunikációs alkalmazások mellett az utóbbi 10-15 évben a fejlődés fő irányát az egyre nagyobb teljesítmények (10.2. ábra), illetve a rövid (ps-fs) impulzushosszak és egyre nagyobb impulzusenergiák elérése jelentette, amelyek új alkalmazási területeket nyitottak meg a szál-lézerek előtt. A nagy, akár 10 kW-ot is elérő teljesítményű, Yb aktív anyagú szál-lézerek kompakt, hatékonyabb, rugalmasabb nyalábvezetésű és gyakran olcsóbb alternatívát jelentenek a CO2 vagy Nd:YAG lézerekkel szemben, ezért egyre szélesebb körben alkalmazzák anyagmegmunkálásra (fémek, műanyagok, kerámiák, üvegek hegesztése, vágása, fúrása, marása, stb.).
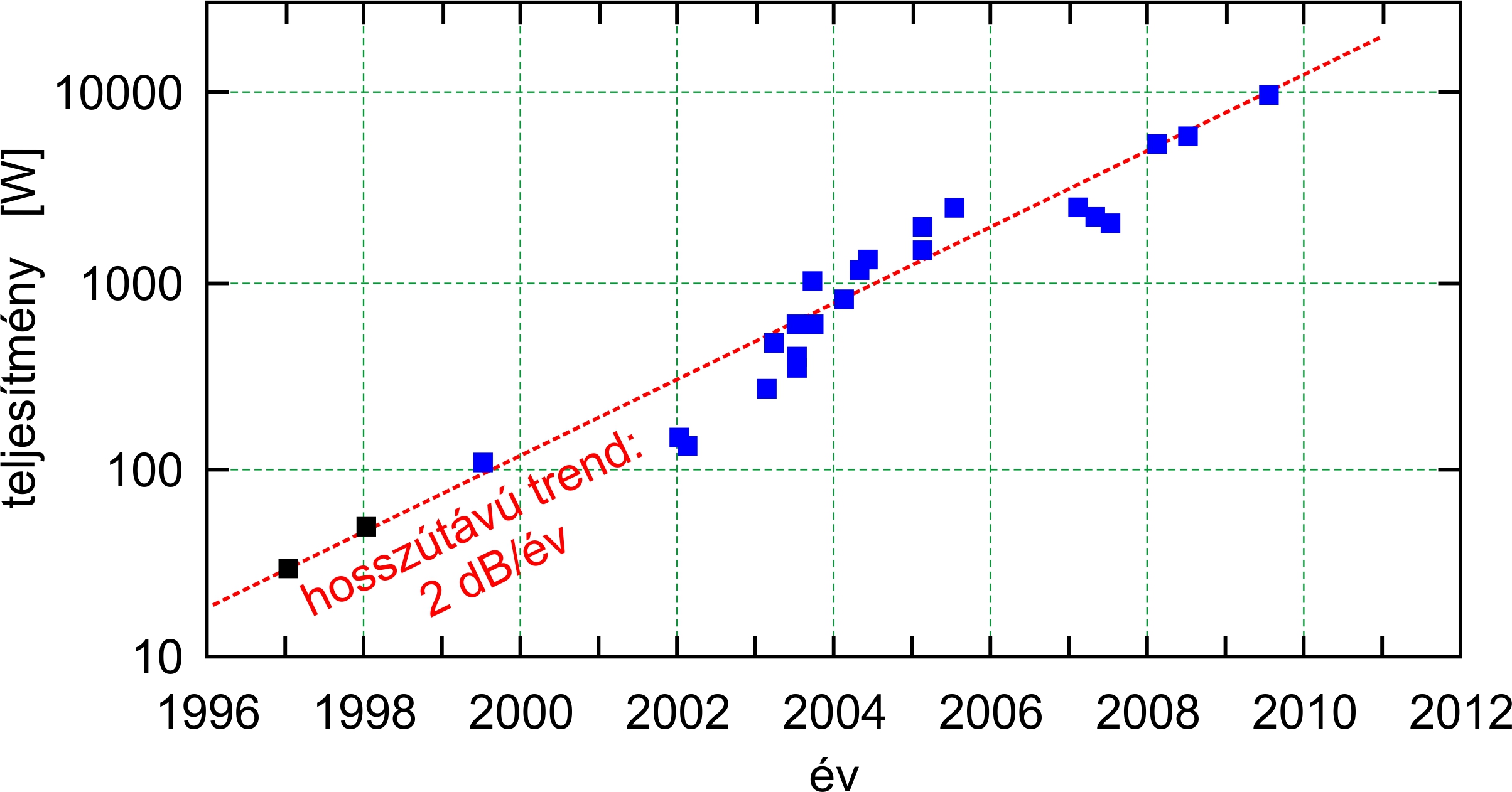
A következőkben röviden áttekintjük az optikai szálakban való fényterjedés alapjait, a szál-lézerek felépítésének és működésének alapjait, valamint a nagy teljesítményű és a rövid impulzusú szál-lézerek néhány jellemzőjét. Átfogóbb tárgyalás, illetve egyes speciális területekről részletesebb áttekintés az irodalomjegyzékben megadott forrásokban található.
Az optikai vagy fényvezető szál a legegyszerűbb esetben egy henger alakú, üvegből készült magból, valamint az ezt körülvevő, kisebb nk törésmutatójú köpenyből álló hullámvezető (10.3. ábra). Az optikai szálban a fény kis veszteséggel ún. módusok formájában terjedhet [10.5, 10.6], amelyeket az elektromágneses tér térbeli eloszlása, valamint a terjedést leíró frekvenciafüggő ún. terjedési állandó [propagation constant] jellemez. A szál fontos jellemzője a mag és köpeny közötti
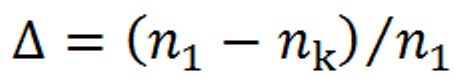 |
(10.1) |
relatív törésmutató-különbség, valamint a módusok számát meghatározó
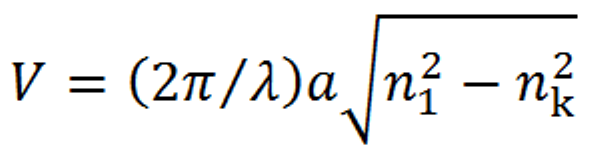 |
(10.2) |
ún. V -paraméter, ahol a mag sugara a és λ a hullámhossz.
Az optikai szálak anyaga leggyakrabban kvarcüveg, amelyben a veszteség 1,55 µm körüli hullámhosszakon rendkívül kicsi, akár 0,16 dB/km ≈ 3,6%/km (ld. a későbbi 10.5. ábrát is). A törésmutató kismértékű megváltozását alacsony koncentrációjú adalékanyagokkal (Ti, Ge, B) lehet elérni. Jellemző értékek n1 ≈ 1,44-1,46 és Δ ≈ 0,001-0,02. A fenti ábrán látható egyszerű lépcsős profilú szalákra V < 2,405 esetén egyetlen módus van (a két lehetséges polarizációs iránytól eltekintve). Ehhez pl. λ = 1,55 μm, n1 = 1,45 és Δ ≈ 0,003 esetén
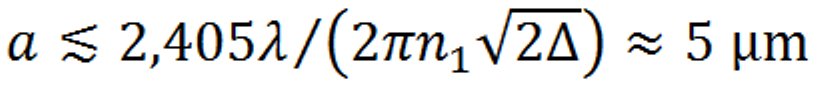 |
(10.3) |
magsugár szükséges; nagyobb sugarak esetén a szál többmódusú [multimode fiber]. A módusok gerjeszthetők, ha az optikai szál bemenetére α < αa = sin-1 NA beesési szöggel fénynyalábot ejtünk (10.3. ábra), ahol
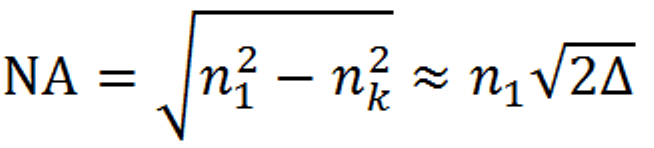 |
(10.4) |
az ún. numerikus apertúra. Ekkor a becsatolt fénynyaláb a mag-köpeny határfelületet a teljes visszaverődés αh = sin-1(nk/n1) határszögénél nagyobb beesési szögben éri.
Rövid impulzusok optikai szálban való terjedésénél fontos szerepet játszik a diszperzió [10.5, 10.6], azaz a terjedési állandó frekvenciafüggése:
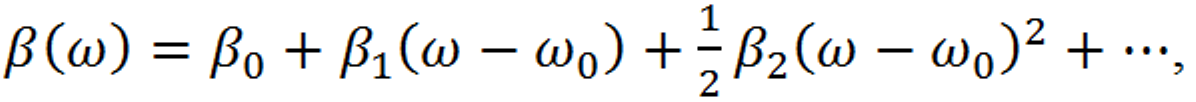 |
(10.5) |
ahol
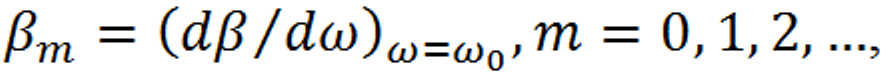 |
. | (10.6) |
és a szál z hosszúságú szakaszán való terjedés során a térerősség Fourier-komponensének fázisa β(ω)z-vel tolódik el. Egymódusú szálakban a diszperzió eredetét tekintve háromféle lehet: anyagi, hullámvezetési, és nemlineáris eredetű diszperzió. Az anyagi diszperzió a mag és a köpeny törésmutatójának hullámhossz-függése miatt lép fel. Kvarcüveg optikai szálakban a β2 ún. csoportsebesség-diszperziós paraméter törésmutatótól eredő járuléka 1,3 µm hullámhossznál zérus. A hullámvezetési diszperzió az adott módus térerősség-eloszlásának a/λ aránytól való függése miatt lép fel. Nagy intenzitásoknál a törésmutató intenzitásfüggő módon megváltozik, ami az impulzusalak megváltozásához vezethet. Többmódusú szálaknál fellép a módus diszperzió is, amely a különböző módusok eltérő csoportsebességeinek a következménye.
A szál-lézerek felépítését vázlatosan a 10.4. ábra mutatja. Az aktív elem egy adalékanyagot tartalmazó maggal rendelkező optikai szál. Az adalékanyag a leggyakrabban valamilyen ritkaföldfém, pl. erbium (Er), neodímium (Nd), itterbium (Yb), holmium (Ho), túlium (Tm), vagy prazeodímium (Pr), amely meghatározza a lehetséges pumpálási és működési hullámhosszakat (ld. 10.1. táblázat). A pumpálást általában egy vagy több lézerdióda biztosítja. A legegyszerűbb esetben a pumpáló fényt az optikai szál magjába csatolják be a szál numerikus apertúrájához illesztett nyalábvezetéssel, amelyet egy lencse biztosít a pumpáló fényt áteresztő, de a lézerfényt reflektáló ún. dikroikus tükrön keresztül (10.4. ábra). Az optikai szál másik végén lévő tükör részben áteresztő, a kimenő lézernyaláb kicsatolása azon keresztül történik. A dikroikus és a kicsatoló tükör alkotják a lézer rezonátorát. A kicsatolt lézernyalábot lencse kollimálja. Az optikai szál általában hajlékony, így azt feltekerve akár nagyobb rezonátorhossz is elhelyezhető igen kis helyen.
|
Lézer-aktív ion |
Hordozó közeg |
Lézer hullámhossz [nm] |
Pumpálási hullámhossz [nm] |
|---|---|---|---|
|
Yb3+ |
kvarcüveg |
1030 - 1100 (975 - 1180) |
900 - 980 |
|
Er3+ |
kvarc-, foszfát- és fluorid üvegek |
1500 - 1600, 2700, 550 |
1480, 1980 |
|
Nd3+ |
kvarc- és foszfátüvegek |
1064 - 1088 (1030 - 1100), 900 - 950, 1320 - 1350 |
808 |
|
Tm3+ |
kvarc-, germánium és fluorid üvegek |
1900 (1700) - 2100, 1450 - 1530, 480, 800 |
793 |
|
Pr3+ |
kvarc- és fluorid üvegek |
1300, 635, 600, 520, 490 |
650 (bonyolultabb pumpálási séma) |
|
Ho3+ |
kvarc- és cirkónium-fluorid üvegek |
2100, 2900 |
1064 |
10.1. táblázat. Szál-lézerekben gyakran használt ritkaföldfém adalékanyagok és hordozó közegek, a jellemző lézer- és pumpálási hullámhosszakkal [10.4, 10.7, 10.8].
Az optikai szál magjának anyaga, amely a lézeraktív ionok hordozó közege, fontos tényező a lézer kimeneti paramétereinek és egyéb tulajdonságainak szempontjából (működési hullámhossz, abszorpciós és emissziós hatáskeresztmetszet, sávszélesség, aktív ionok koncentrációja, stb.). A legfontosabb követelmény az, hogy a hordozóanyag átlátszó legyen a lézer hullámhosszán. A látható és közeli infravörös tartományban leggyakrabban használt hordozó a kvarcüveg (10.1. táblázat), amelyet rendkívül kis csillapítása miatt a telekommunikációban is használnak (10.5. ábra). A foszfátüvegek előnye a kvarcüveggel szemben az, hogy nagyobb ritkaföldfém-koncentrációt és így nagyobb hosszegységre eső erősítési tényezőt tesz lehetővé. A cirkónium-fluorid alapú szálak az infravörös tartományban jelentenek alternatívát a kvarc helyett, amely a 2 µm-nél hosszabb hullámhosszakon erősen abszorbeál.
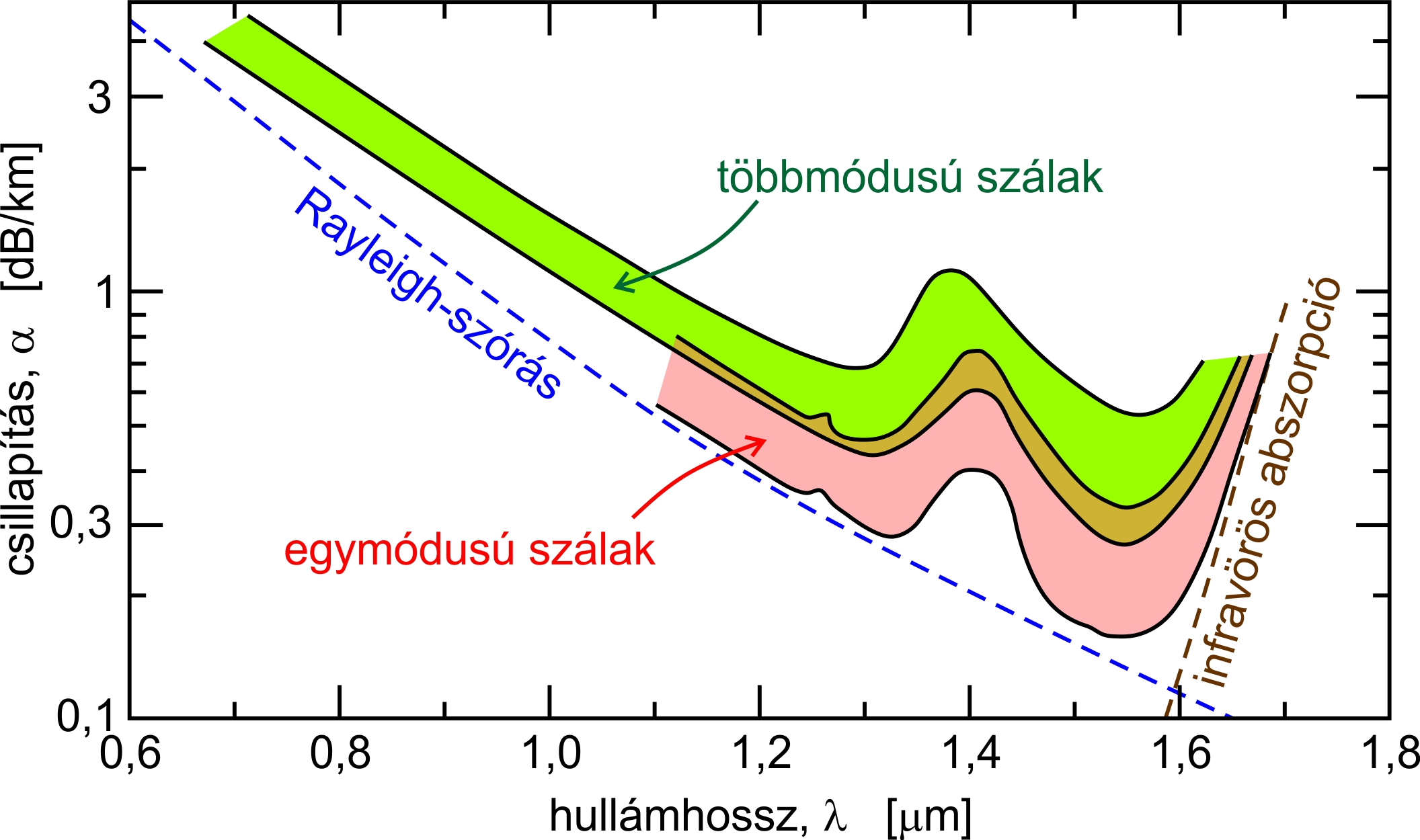
Fotoszenzitív üvegből készült magban UV fénnyel való besugárzás hatására permanens törésmutatóváltozás hozható létre. Hosszirányban periódikus vagy aperiódikus besugárzással törésmutató rács, ún Bragg-rács [fiber Bragg grating] hozható létre, amely jellemzően néhány száz nm-es periódusú és néhány mm vagy cm hosszúságú. Bragg-rácsot gyakran használnak keskenysávú szál-lézerek rezonátorának végtükreként. Az ilyen integrált megoldások többek között jelentősen javíthatják a szál-lézerek stabilitását és megbízhatóságát, mert a fénynek nem kell kilépnie a levegőbe. Megfelelő aperiódikus törésmutató-modulációjú Bragg-rácsok, az ún. csörpölt Bragg-rácsok diszperziókompenzálásra, és így rövid impulzusok időbeli összenyomására is használhatók pl. csörpölt impulzusú erősítő (CPA) rendszerekben (ld. 5. fejezet).
A szál-lézerek felépítésükből adódóan több előnyös tulajdonsággal bírnak. A nagy abszorpciós hossz miatt kiemelkedően jó hatásfokú pumpálás lehetséges: a felvett elektromos teljesítménynek jellemzően 30 - 40%-a a kimenő lézerteljesítmény (ez az érték szilárdtest- vagy gázlézereknél általában 1% alatti). A nagy erősítési hossz miatt nagy erősítési faktor érhető el, amely nagy (~90%-os) rezonátorbeli veszteségeket is megenged. A kis keresztmetszet és a nagy felület miatt a termikus effektusok általában nem jelentősek. A hullámvezetés miatt a kimenő lézernyaláb minősége általában nagyon jó. A levegőben való nyalábterjedés részben vagy egészen kiküszöbölhető, ami a szál-lézerek stabilitását jelentősen növeli, azok kevésbé érzékenyek a környezeti hatásokra. Kedvezőtlen tulajdonság, hogy a kis keresztmetszet korlátozza a teljesítmény vagy az impulzusenergia növelését. A nagy hossz miatt nemkívánatos nemlineáris jelenségek léphetnek fel már viszonylag alacsony intenzitásoknál is.
A nagy, akár 10 kW-ot is elérő teljesítményű szál-lézerek kifejlesztését több technológiai tényező tette lehetővé. Az Yb aktív anyagú szál-lézerek különösen alkalmasak nagy teljesítmények elérésére mind folytonos, mind impulzusüzemben. Ennek fő oka (i) a rendkívül kicsi kvantumdefektus a 900 - 980 nm hullámhossztartományba eső pumpálás esetében (ld. 10.1. táblázat), ami kicsi disszipálandó hővel jár, illetve (ii) magas Yb koncentráció, ami hosszegységre vonatkoztatott nagy abszorpciót és így hatékony pumpálást tesz lehetővé. Az Yb illetve másfajta aktív anyagú szál-lézerek teljesítménynövelésének további fontos tényezői a nagyteljesítményű pumpáló lézerdiódák, valamint az ún. kettős köpenyű optikai szálak [double-clad fiber] alkalmazása. Utóbbi tette lehetővé a köpenyen keresztül való pumpálást [cladding pumping] (10.6. ábra).
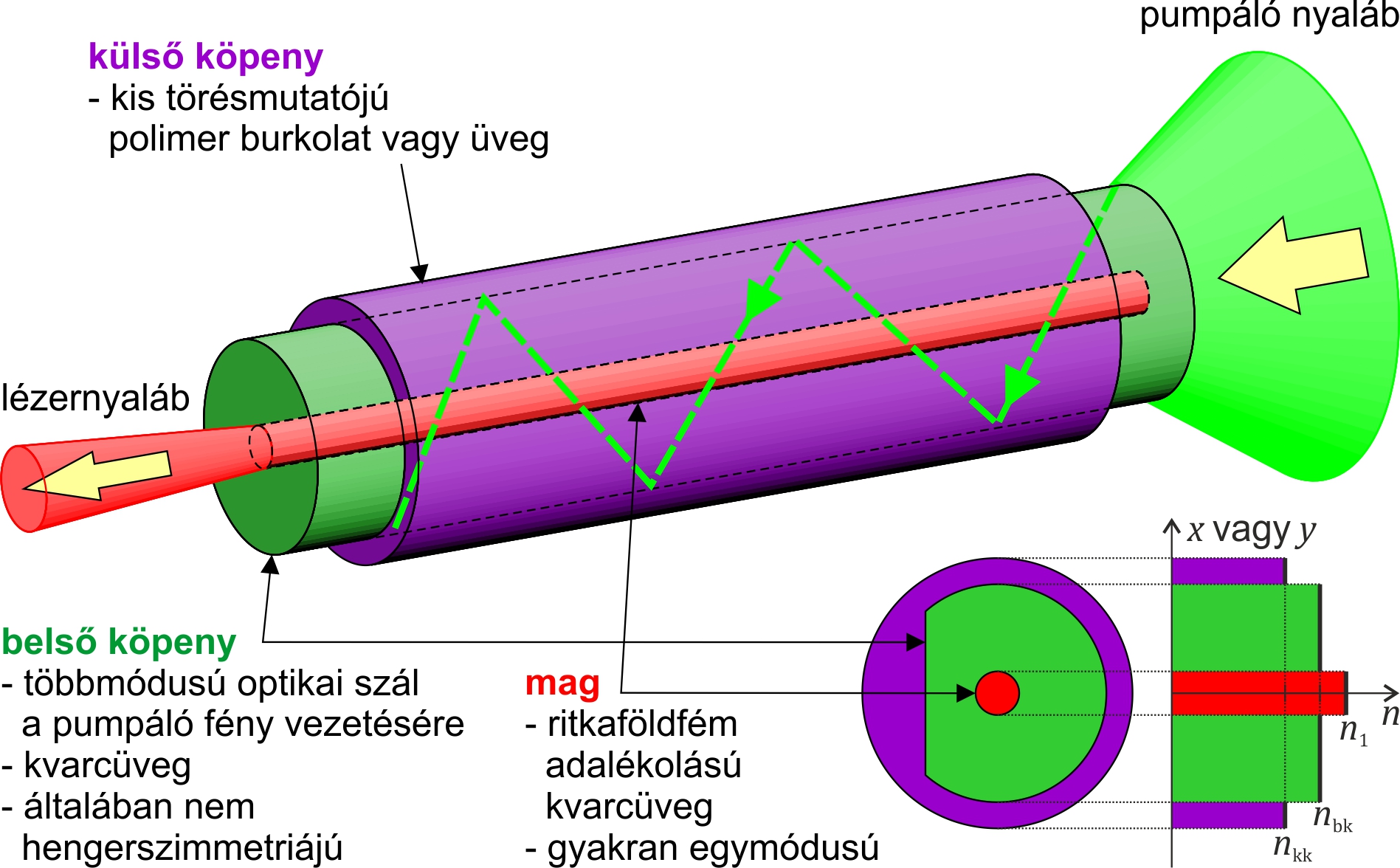
A kettős köpenyű optikai szálakban a ritkaföldfém adalékolású magot a jóval nagyobb keresztmetszetű, a magnál kisebb törésmutatójú belső köpeny, azt pedig egy külső köpeny veszi körül (10.6. ábra). A mag és a belső köpeny által alkotott hullámvezető általában egymódusú, ebben terjed az erősítendő lézerfény. A belső köpeny a nála kisebb törésmutatójú külső köpennyel együtt szintén hullámvezetőt alkot. A pumpáló nyalábot a belső köpenybe csatolják be és a szálban való terjedés során fokozatosan abszorbeálódik az adalékolt magban. A külső hullámvezető nagyobb keresztmetszetének köszönhetően jóval nagyobb pumpáló teljesítmény használható. A kW skálájú szál-lézereknél a belső köpeny átmérője akár közel 1 mm is lehet, a magé 40 µm körüli; a megfelelő keresztmetszetek aránya kb. 400. Bonyolultabb architektúrájú szál-lézerek kisebb, 100 µm körüli átmérőjű szálakat használnak, általában több, egymás utáni erősítőfokozatban.
Az elérhető nagy átlagteljesítmények mellett a szál-lézerek másik fő vonzereje a rendelkezésre álló impulzushosszak igen széles skálája. Az üveg hordozóba ültetett ritkaföldfém-ionok igen nagy emissziós sávszélességének köszönhetően a folytonos üzemtől egészen a néhány fs impulzushosszig építhetők szál-lézerek. Szál-lézerek segítségével extrém rövid, 4,5 fs impulzushosszú egyciklusú fényimpulzusokat is sikerült előállítani [10.9]. Az impulzushosszat a diszperzió, a nemlineáris effektusok és az erősítés, valamint ezek kapcsolata határozza meg.
A ps-os - fs-os impulzushosszak tartományában - a rúdlézerekhez hasonlóan - módusszinkronizálásra van szükség. Megjegyezzük, hogy itt a lézerrezonátor különböző frekvenciájú, azaz longitudinális módusainak fázisbeli szinkronizálásáról van szó, amely nem keverendő össze a hullámvezető szál módusaival; utóbbi elsősorban a térerősség keresztirányú eloszlását írja le. Aktív módusszinkronizálás lehetséges pl. (rezonátorba integrált) elektro-optikai vagy akuszto-optikai modulátorok segítségével. Passzív módusszinkronizálás lehetséges többek között félvezető anyagú telítődő abszorber [semiconductor saturable absorber mirror] (SESAM) alkalmazásával (10.7. ábra). Az aktív technikákat általában nagy ismétlési frekvenciájú ps-os impulzusok előállítására használják; a passzív technikák elsősorban ultrarövid (fs-os) impulzusok keltésére alkalmasak.
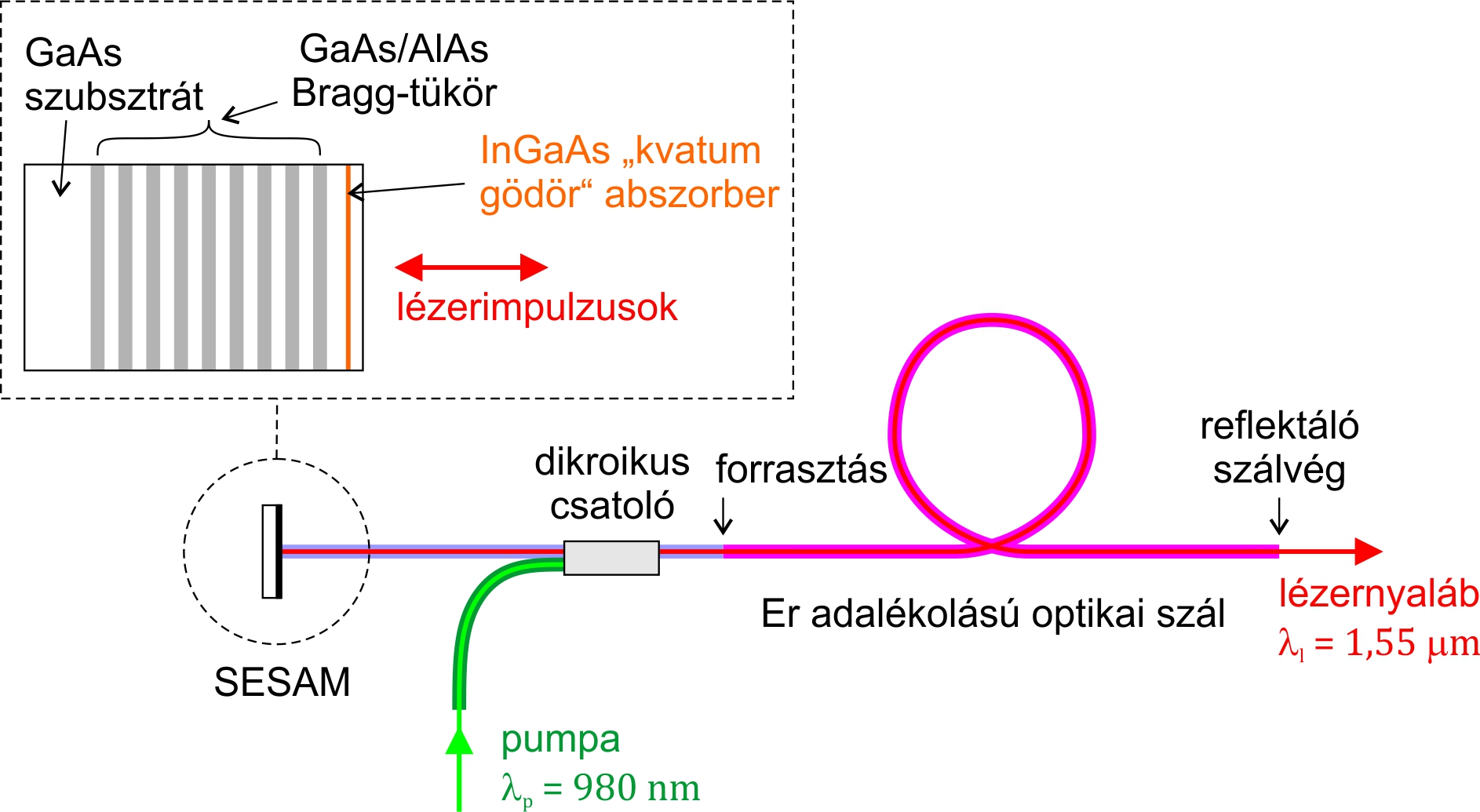
A nemlineáris polarizációforgatás jelenségén [10.6] alapul egy további, speciálisan a szál-lézereknél használatos passzív módusszinkronizálási módszer. A nemlineáris polarizációforgatás az ún. ön-fázismoduláció és kereszt-fázismoduláció jelenségén - ezek harmadrendű nemlineáris optikai effektusok - , valamint az optikai szálakban előforduló (véletlen) kettőstörésen alapul. Az optikai szálak - még a névleg egymódusú szálak is - a valóságban általában kettőstörést mutatnak. Ennek mértéke a
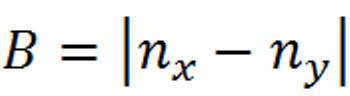 |
(10.7) |
kettőstörési paraméterrel jellemezhető, ahol nx és ny a két, egymásra merőleges polarizációs főirányban a törésmutató. Nagy intenzitásoknál mindkét törésmutató intenzitásfüggő módon megváltozik [10.6]:
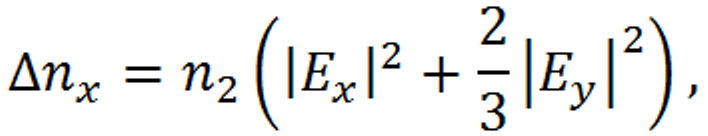 |
(10.8) |
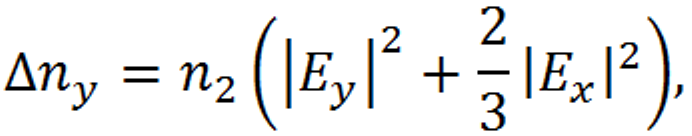 |
(10.9) |
ahol Ex és Ey a két polarizációs főirányhoz tartozó térerősség-amplitúdók, amelyeket a bejövő fény polarizációs állapota határoz meg. Ha az optikai szál kimenetére egy polarizátort helyezünk (10.8. ábra), annak transzmissziója intenzitásfüggő lesz és az elrendezés gyors telítődő abszorberként használható. A bejövő fény polarizációs állapotát, valamint a polarizátor áteresztési irányát alkalmas módon beállítva elérhető, hogy a transzmisszió az intenzitás-csúcsnál legyen maximális. Pl. az x irányhoz képest Θ irányban lineárisan polarizált bemenő fény, valamint erre merőleges irányú áteresztéssel rendelkező polarizátor esetében a transzmisszió a következő lesz [10.6]:
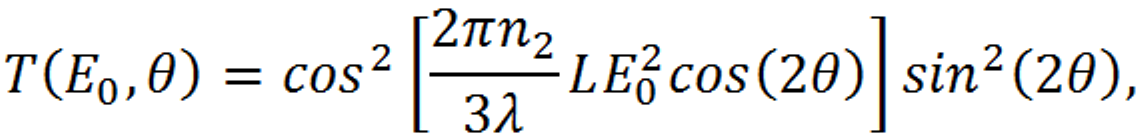 |
(10.10) |
ahol E0 az elektromos térerősség amplitúdója, n2 az ún. nemlineáris törésmutató, λ a hullámhossz és L az optikai szál hossza. A fenti összefüggés szerint kis intenzitásokra a transzmisszió közel 0, nagy intenzitásoknál megfelelő Θ szögnél nagy, akár 100%-hoz közeli transzmisszió is elérhető (10.9b. ábra (animáció)).
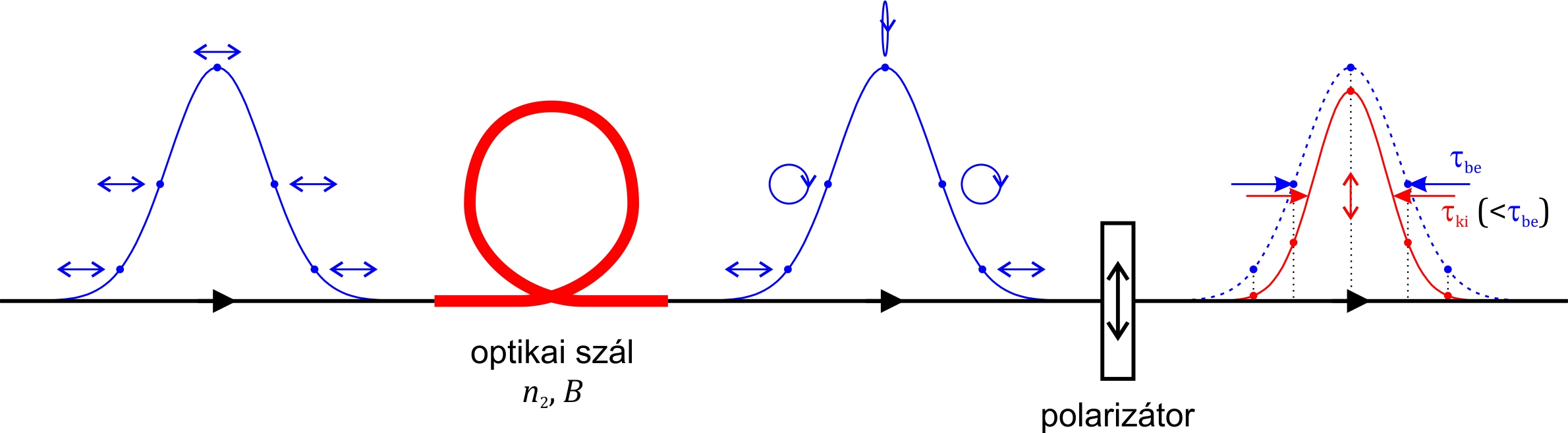
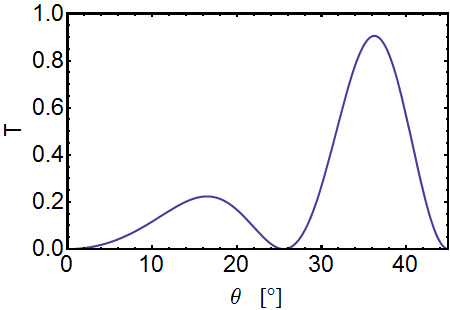
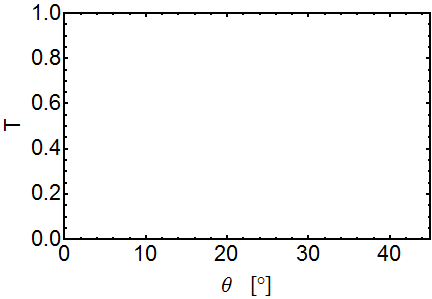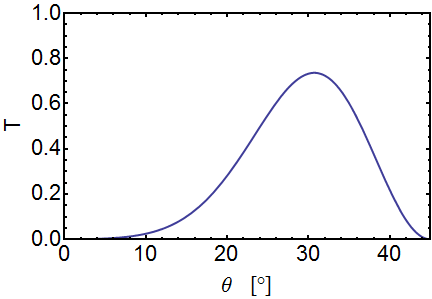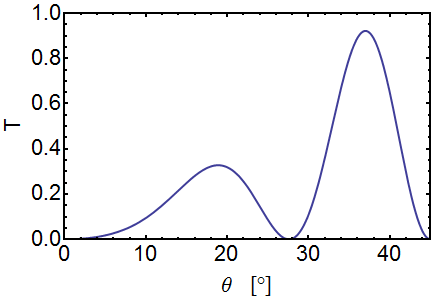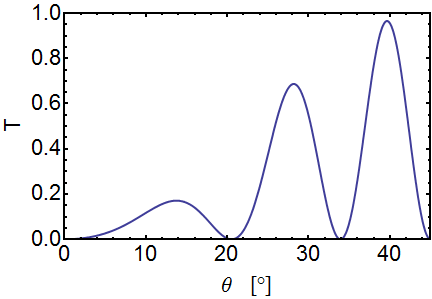
A rövid (fs-os) impulzusok keltése szempontjából a szál-lézerek számos kedvező tulajdonsággal rendelkeznek. Azonban a nagy közegbeli propagációs hossz miatt a diszperzió és különösen a nemlineáris effektusok erősen limitálják a módusszinkronizált szál-lézerekkel elérhető impulzusenergiát, impulzushosszat és egyéb jellemzőket. Szál-lézerek esetében az oszcillátorból kicsatolható impulzusenergia jellemzően a 10 pJ - 1 nJ tartományban van. Egyszerű optikai szál alapú utóerősítéssel az impulzusenergia további egy-két nagyságrenddel növelhető meg. Még nagyobb impulzusenergiák eléréséhez speciális utóerősítési technikákat használnak, amelyek közül a két legfontosabb a parabolikus impulzuserősítés [parabolic pulse amplification] és az optikai szálban való csörpölt impulzusú erősítés (az angol név [chirped-pulse amplification] alapján a továbbiakban CPA). Az előbbi technikával a µJ-os, utóbbival akár a mJ-os energiaszint is elérhető.
Parabolikus impulzuserősítés: Normális diszperzióval rendelkező optikai szálban megfelelő körülmények esetén az impulzus egyre növekvő lineáris csörpre tesz szert az erősítési folyamat során, ami egyre növekvő impulzushosszat eredményez. Ez az impulzushossz-növekedés részben ellensúlyozza a növekvő impulzusenergiával járó egyre nagyobb csúcsteljesítményt, ami így az energiánál lényegesen lassabban növekszik. Végeredményben a szál roncsolódása nélkül jóval nagyobb, akár µJ szintű kimenő impulzusenergiát lehet elérni, mint más körülmények esetén. Ezt a technikát parabolikus impulzuserősítésnek, az ilyen elven működő szál-lézereket szimilariton lézereknek nevezik. Az elnevezések oka az, hogy a kialakuló impulzus intenzitásának időfüggése parabola alakú, az impulzusalak pedig az erősítési folyamat során önhasonló módon változik. Az erősített impulzusok időbeli összenyomása pl. a CPA lézereknél megszokott módon külső, rácsos vagy prizmás kompresszorral lehetséges.
Optikai szál alapú CPA: A szál-lézerekkel eddig elért legnagyobb, akár 1 mJ-t is meghaladó impulzusenergiákat a nagyintenzitású lézereknél széles körben alkalmazott CPA technika segítségével érték el. Az erősítendő rövid (~100 fs körüli hosszúságú) impulzusokat alkalmas, nagy diszperzióval rendelkező elemmel időben megnyújtják (jellemzően ~1 ns körüli hosszra). A nyújtás megoldható pl. hosszú, diszperzív egymódusú szálban, rácsos impulzusnyújtóval vagy csörpölt Bragg-ráccsal. Az impulzus csúcsintenzitása a nyújtási faktor arányában csökken, így az nagy energiára erősíthető anélkül, hogy túlzott mértékű ön-fázismoduláció lépne fel, illetve a szál roncsolódna. Az erősített impulzusok eredeti hosszra való összenyomásával rendkívül nagy csúcsintenzitás érhető el. Az összenyomás általában rácsos kompresszorral történik, de alkalmazhatók (szál-integrált vagy térfogati) Bragg-rácsok, illetve üreges magú fotonikus kristály szálak is. Az szál-alapú CPA rendszereknél a kimenő nyaláb jó minősége miatt általában igen kicsi, néhány µm2-es fókuszfolt érhető el, amellyel a jövőben akár 1016 - 1017 W/cm2-es csúcsintenzitások is elérhetővé válnak majd.
Számítsa ki és hasonlítsa össze különböző architektúrájú (rúd-, korong-, illetve szál-) lézerek egyutas erősítését! A számításhoz tipikus koncentrációjú Yb-adalékolást, tipikus pumpáló intenzitást, valamint tipikus geometriai méreteket vegyen alapul!
Adja meg azt a terjedési hosszat, amelynek befutása során egy optikai szálba becsatolt fény teljesítménye a felére csökken, ha a szálban a veszteség (a) 0,2 dB/km, (b) 20 dB/km, illetve (c) 2000 dB/km. Adja meg a megfelelő α abszorpciós együtthatót is cm-1 egységben!
Egy fényvezető szál magjának sugara α = 5 µm, törésmutatója n1 = 1,45. A mag és a köpeny relatív törésmutató-különbsége Δ = 0,002. Határozza meg a legrövidebb hullámhosszat, amelyre a szál egymódusú!
A 7,9%-os Ge adalékolású kvarcüveg törésmutatójának hullámhosszfüggését megadó Sellmeier-formulában szereplő konstansok a következők: B1 = 0,7136824, B2 = 0,4254807, B3 = 0,8964226, λ1 = 0,0617167 µm, λ2 = 0,1270814 µm, λ3 = 9,896161 µm. Ábrázolja az n törésmutatót, az ng csoport-törésmutatót és a β2 csoportsebesség-diszperziós paramétert a hullámhossz függvényében a 0.5 - 1.6 µm tartományon! Adja meg a zérus diszperzió hullámhosszán - azaz ahol β2(λ0) = 0 teljesül - a β3 és β4 harmad- és negyedrendű diszperziós paramétereket!
Vezesse le a (10.3) egyenletet!
[10.1] E. Snitzer, Proposed fiber cavities for optical lasers, J. Appl. Phys., vol. 32, p. 36, 1961.
[10.2] C. J. Koester and E. Snitzer, Amplification in a fiber laser, Appl. Opt., vol. 3, p. 1182, 1964.
[10.3] R. J. Mears, L. Reekie, I. M. Jauncey and D. N. Payne, Low-noise erbium-doped fibre amplifier operating at 1.54 µm, Elecron. Lett., vol. 23, p. 1026, 1987.
[10.4] D. J. Richardson, J. Nilsson and W. A. Clarkson, High power fiber lasers: current status and future perspectives, J. Opt. Soc. Am. B, vol. 27, p. B63, 2010.
[10.5] B. E. A. Saleh és M. C. Teich, Fundamentals of photonics, Wiley, 1991.
[10.6] G. P. Agrawal, Nonlinear fiber optics, Academic Press, 2007.
[10.7] OP-TEC: The National Center of Optics and Photonics Education, Fiber Laser Basics, 2011. [Online]. Available: http://www.op-tec.org/.
[10.8] R. Paschotta, Encyclopedia of Laser Physics and Technology, Berlin: Wiley-VCH, 2008.
[10.9] G. Krauss, S. Lohss, T. Hanke, A. Sell, S. Eggert, R. Huber and A. Leitenstorfer, Synthesis of a single cycle of light with compact erbium-doped fibre technology, Nat. Photonics, vol. 4, p. 33, 2010.
Tartalom
1966-ban Sorokin és Lankard [11.1] illetve Schäfer és munkatársai [11.2] egymástól függetlenül fedezték fel, hogy szerves festékek híg oldata is használható lézerek aktív anyagaként. Az azóta eltelt idő alatt több mint kétszáz fajta festékkel sikerült lézerfényt előállítani. Ezeket a festékeket a szerkezetük szerint több csoportra oszthatjuk (pl. xantének, kumarionok, stb.). Oldószerként etanol, metanol, stb. használható. A festéklézer gerjeszthető villanólámpával vagy egy másik lézerrel. Általában a festéklézereket impulzusüzemben működtetik, ekkor a pumpáló lézer is impulzuslézer (pl. N2-lézer vagy excimer lézer), de folytonos üzemben is működtethető, ha a pumpáló lézer folytonos lézer (pl. argon-ion lézer). A festéklézerek fő előnye, hogy különböző festékeket használva széles hullámhossztartományban folytonosan hangolhatók, így a spektroszkópiának egy igen kedvelt lézertípusa.
A festékmolekulák nagyméretű, bonyolult szerkezetű, szerves molekulák, több gyűrű alakú struktúrából tevődnek össze. Az ultraibolya, a látható és a közeli infravörös tartományon erős abszorpcióval és fluoreszcenciával bírnak. A 11.1. ábrán látható egy, a festéklézerekben gyakran használt festékmolekula, a Rodamin 590 szerkezeti képlete, valamint az abszorpciós és emissziós spektruma. Jelentős abszorpcióval a 200-350 nm, 450-550 nm illetve 600-800 nm közötti tartományon bír, a maximális abszorpció 530 nm környékén van. Ebből következőleg ez a festékmolekula hatékonyan gerjeszthető az 532 nm-en működő frekvenciakétszerezett Nd:YAG lézerrel, vagy pl. a KrF excimer lézerrel, amely 248 nm-en bocsát ki fényt. De még a nitrogénmolekula-lézer is használható, amely a 337 nm körüli hullámhossz tartomány néhány nm szélességű sávjában sugároz, ami egybeesik a festékmolekula egyik lokális abszorpciós csúcsának környezetével. A gerjesztett festékmolekula fluoreszcencia spektruma az 530-670 nm közötti hullámhossztartományt fedi le, a csúcsa 550 nm-nél van. Látható, hogy a fluoreszcencia spektrum eltolódik a hosszabb hullámhosszak felé a szinglett állapotok közötti átmenethez tartozó abszorpciós spektrumhoz képest, és így kicsi az átfedés, ami előnyös a lézerműködés szempontjából. Azonban a triplett állapotokhoz tartozó abszorpció átfed az emisssziós spektrum hosszabb hullámhosszú részével, ami a lézerműködést hátrányosan befolyásolja, de erre részletesebben a későbbiekben térünk ki.
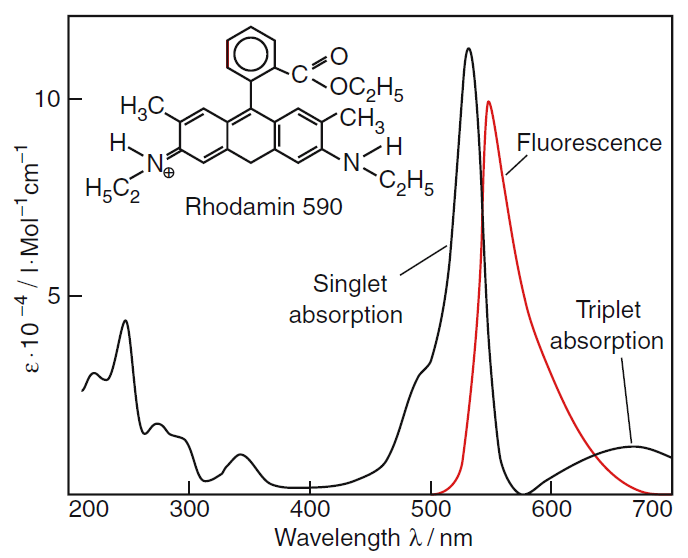
11.1. ábra. A Rodamin 590 festékmolekula abszorpciós és emissziós spektruma. Betétábra: a festékmolekula szerkezeti képlete [11.3].
A festékmolekulák tipikus energiaszint diagramját mutatja a 11.2. ábra. A bonyolult molekulaszerkezet miatt számos rotációs-vibrációs nívóval rendelkeznek az S0 szinglett alapállapotban és a gerjesztett állapotokban (S1 szinglett és T1, T2 triplett állapotokban). A festékmolekuláknak az oldószerrel való erős kölcsönhatása azt eredményezi, hogy az átmenetek kiszélesednek. A kiszélesedés mértéke nagyobb, mint az átlagos távolság a rotációs-vibrációs szintek között. Így a sok diszkrét abszorpciós és emissziós vonal helyett abszorpciós és emissziós sávokat kapunk.
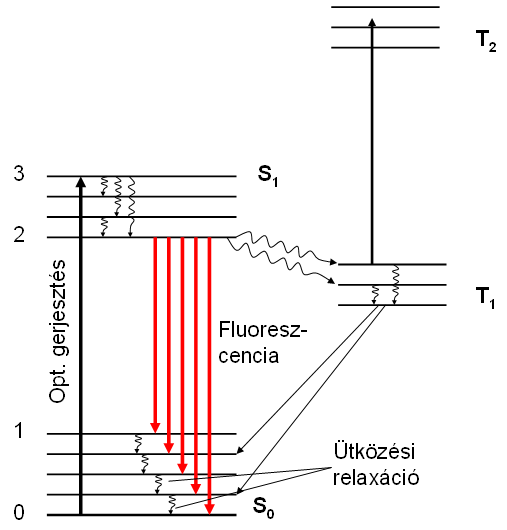
11.2. ábra. A festékmolekulák tipikus energiaszint diagramja.
A festékmolekulákat megfelelő frekvenciájú fénnyel megvilágítva az S0 alapállapot legalsó nívójáról (0. szint) az S1 gerjesztett állapot legfelső nívóira (3. szint) jutnak. Sávon belüli energiacserével a gerjesztett festékmolekulák néhány pikoszekundumon belül relaxálódnak az S1 állapot legalacsonyabb nívójára (2. szint) kerülve. Az átmenetkor felszabaduló energia az oldószer hőmérsékletének növekedésére fordítódik.
A molekulák az S1 sáv legalsó nívóiról sugárzásos átmenettel, spontán emisszió vagy indukált emisszió keretében fluoreszcencia fényt kibocsátva átkerülnek az S0 állapot felsőbb rotációs-vibrációs nívóira (1. szint). Mivel ezen nívók betöltöttsége szobahőmérsékleten a Boltzmann-eloszlást követi, így gyakorlatilag betöltetlenek. Ennek eredményeképpen populáció inverzió érhető el az 1. és 2. szintek között, ha a 2. szintre optikai gerjesztéssel megfelelő mennyiségű molekulát jutattunk. Az alsó lézernívó (1. szint), azaz az S0 sáv felsőbb nívóinak kiürülése szintén gyors sávon belüli energiacserével történik. Ebből következőleg a festéklézer működése egy négy-nívós (0., 1., 2., 3. szint) lézerműködésnek felel meg. Mivel az 1. és a 3. szintről nagyon rövid időn belül átmennek a molekulák a 0. és 2. szintre, így ezeken a szinteken a populáció elhanyagolhatóan kicsi. Ezért a festéklézerekkel a küszöbfeltétel már nagyon kicsi populáció inverzióval is elérhető. A felső lézernívó rövid (nanoszekundumos) élettartama miatt a festéklézerek nagy pumpaintenzitást igényelnek a küszöbfeltétel eléréséhez.
Mivel az abszorpció hatására a molekula az S0 sáv alsó nívóiról az S1 sáv felső nívóira gerjesztődik, viszont az emisszió során az S1 sáv alsó nívójáról az S0 felsőbb nívóira jut, így a festékoldat emissziós spektruma az abszorpciós spektrumhoz képest a hosszabb hullámhosszak felé tolódik el, ahogy ezt már megállapítottuk a 11.1. ábra alapján is. Ily módon kicsi az átfedés az abszorpciós és emissziós spektrumban, azaz nem nyeli el a molekula az általa kibocsátott fluoreszcencia fényt.
Az S1 nívóról nemcsak sugárzásos átmenettel mehetnek a molekulák az S0 nívókra, hanem kis valószínűséggel az S1-T1 sugárzásmentes átmenet is megvalósulhat. Igy a triplett nívóknak a lézerműködésre gyakorolt hatását is figyelembe kell vennünk. A T1 triplett állapot élettartama 100 ns körüli érték. Ez az állapot két módon befolyásolja a lézerműködést. Egyrészt relatíve hosszú ideig maradnak a T1 állapotba került molekulák ebben az állapotban, azaz csapdázódnak, így csökken a populáció inverzió létrehozásához felhasználható molekulák száma. Másrészt a T1-T2 átmenethez tartozó abszorpciós spektrum részben átfed az emissziós spektrummal, így elnyeli a keletkező lézerfény egy részét (11.1. ábra). Ezért rövid gerjesztő impulzusokat kell használnunk, illetve folyamatosan áramoltatni kell a festékoldatot a küvettában. Folytonos üzemű festéklézernél a festékoldatot kb. 10 m/s sebességgel áramoltatják a gerjesztési régióban. A festékoldat keringtetésére amiatt is szükség van, hogy elkerüljük a festék túlmelegedését, illetve a festékmolekulák fotodegradációját.
Spektroszkópiai vizsgálatoknál gyakran olyan fényforrásra van szükség, hogy egyrészt keskeny spektrummal rendelkezzen, másrészt hangolható legyen. Az előbbi fejezetben láttuk, hogy a festéklézer fénye alapvetően széles spektrummal bír. Ebből a spektrumból egy vékony, néhány tized nanométer szélességű spektrumvonal azonban kiválasztható a rezonátorba helyezett hullámhossz-szelektor optikai elemmel (pl. prizmával, optikai ráccsal). Speciális optikai elemekkel ennél 4-5 nagyságrenddel kisebb sávszélesség is előállítható. Hangolva ezen optikai elemnek a transzmissziós csúcsát, a lézer hullámhossza is megfelelően hangolódik. A hangolási tartomány egy-egy festék esetén 30-60 nm, ami kicsit kisebb, mint az emissziós sávszélesség. Mivel a különböző színű festékek különböző hullámhossztartományban emittálják a fényt (11.3. ábra), így a küvettában cserélve a festékoldatot, 400 nm-től 1000 nm-ig állíthatunk elő lézerfényt.
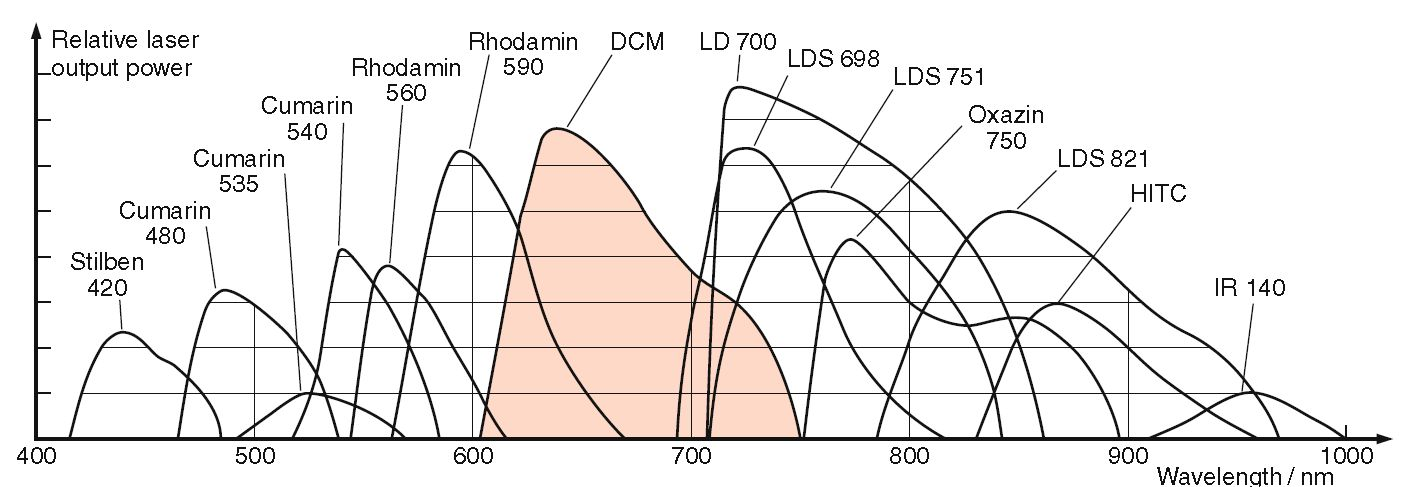
11.3. ábra. Különböző festékek hangolási tartománya [11.3].
A 11.4. ábrán látható a festéklézer felépítése, ha villanólámpát használunk gerjesztésre. A gerjesztés geometriája megegyezik a szilárdtestnél alkalmazott megoldással, azaz egy elliptikus tükör egyik fókuszvonala mentén helyezkedik el a villanólámpa, míg a másik fókuszvonal mentén pedig a festékes küvetta (11.4.b ábra).
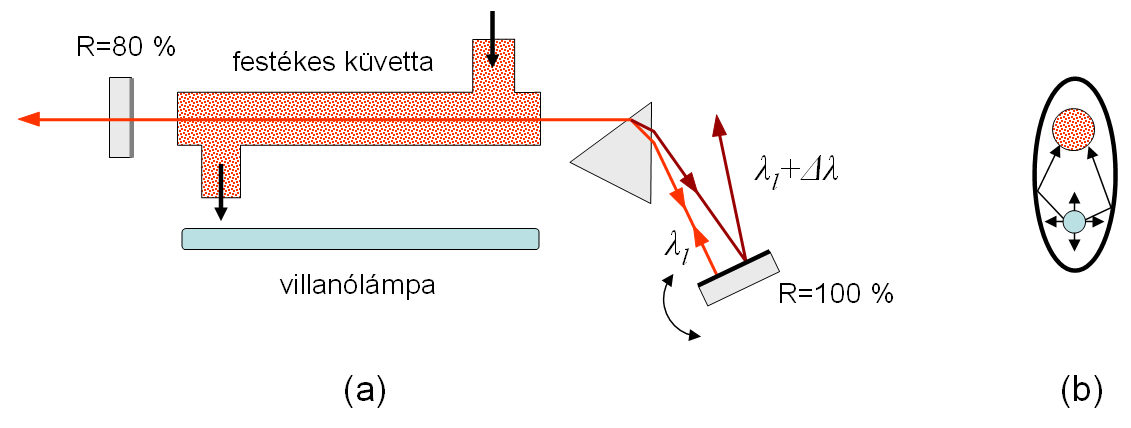
11.4. ábra. (a) Hangolható festéklézer gerjesztése villanólámpával. (b) A gerjesztés geometriája.
A festékoldatot folyamatosan áramoltatni kell, melyet egy szivattyúval oldhatunk meg. A 11.4. ábrán a rezonátorban elhelyezett hullámhossz-szelektor optikai elem egy üvegprizma. Mivel a festékes küvettából a tengelyének irányában kilépő széles spektrumú fény különböző hullámhosszú komponenseit a prizma különböző irányokba téríti el, így csak egy bizonyos λ l hullámhosszú komponens fog önmagába visszaverődni a tükörről, azaz csak ez a hullámhosszú komponens fog visszajutni a küvetta tengelyének irányába. A 100 % reflexiójú végtükör forgatásával változtatni tudjuk ezt a hullámhosszat.
Egy másik megoldás, amikor egy impulzuslézert használunk a festékoldat gerjesztésre (11.5. ábra). Ez a lézer lehet például excimer lézer vagy N2-lézer.
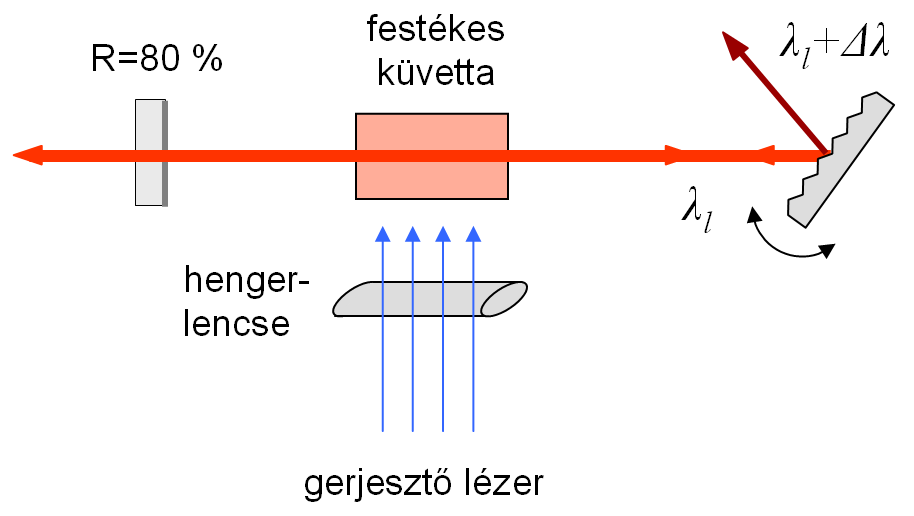
11.5. ábra. Impulzus üzemű lézerrel gerjesztett, optikai ráccsal hangolható festéklézer.
A gerjesztő lézer nyalábját ráfókuszáljuk egy hengerlencsével a festékes küvettára. Ily módon a lencse fókuszvonalában gerjesztődik a festék molekula. A küvettából kilépő, a fókuszvonal irányában haladó, széles spektrumú fluoreszcencia fény egy optikai rácsra esik be. A széles spektrumból a küvetta tengelyének irányába csak az a λ l hullámhosszú komponens fog diffraktálódni a rácsról, amelyik eleget tesz a Littrow-feltételnek, azaz
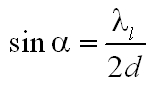 |
, | (11.1) |
ahol d a szomszédos rácskarcolatok távolsága és α a beesési illetve egyúttal a diffrakciós szög. Mivel a λ l + Δλ komponensre más a diffrakció szöge, így nem teljesül a (11.1) feltétel, ezért ez a hullámhosszú fény a diffrakció után már nem a küvetta tengelyének irányában halad. Ily módon csak a λ l hullámhosszú fény fog erősödni, pontosabban a kibocsátott lézerfény spektrumának félértékszélessége néhány nanométer lesz.
A rácsról diffraktált fény spektrumának félértékszélességét a rács λ/δλ spektrális felbontóképessége határozza meg:
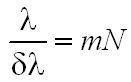 |
, | (11.2) |
ahol m a diffrakció rendje és N a rács megvilágított karcolatainak száma. Mivel a vékony lézernyaláb miatt kevés karcolat van megvilágítva a 11.5. ábrán látható elrendezésben, ezért egy megoldás, ha súrlódó beesésben világítjuk meg a rácsot (11.6. ábra).
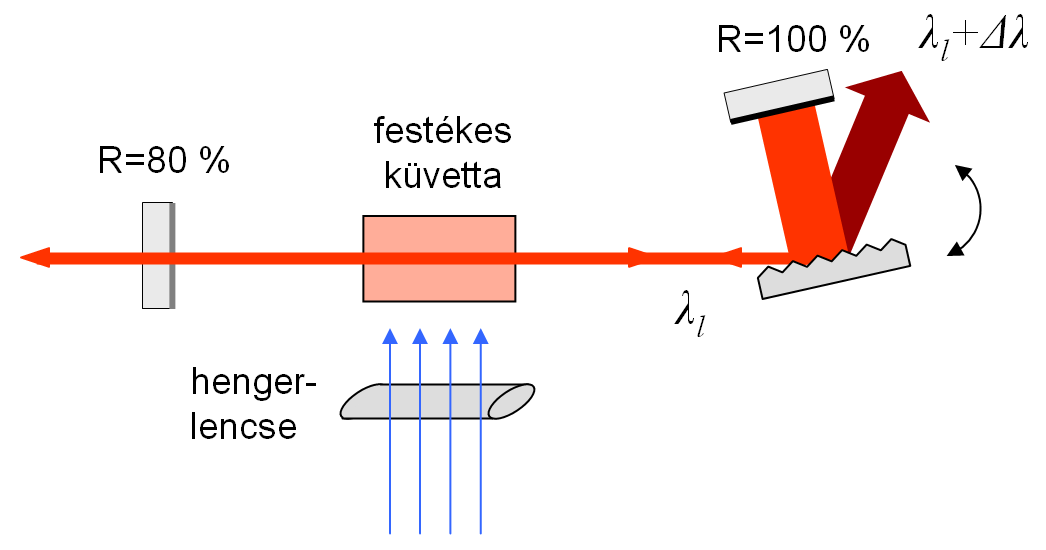
11.6. ábra. Hangolható festéklézer súrlódó beesésben megvilágított ráccsal.
Ennél a megoldásnál a rács a 11.5. ábrán látható beállítástól eltérően nem Littrow elrendezésben van, így szükség van egy végtükörre, mely a kiválasztott hullámhosszat veri vissza. A súrlódó beesés miatt az eredetileg vékony lézernyaláb elég nagy felületen világítja meg a rácsot, így a (11.2) alapján a felbontóképesség nagyobb lesz, azaz a spektrum δλ félértékszélessége lecsökken. Egy másik megoldás, ha továbbra is Litrow-elrendezésben világítjuk meg a rácsot, de előtte egy teleszkópikus elrendezésben kitágítjuk a lézernyalábot az eredeti átmérőjének sokszorosára.
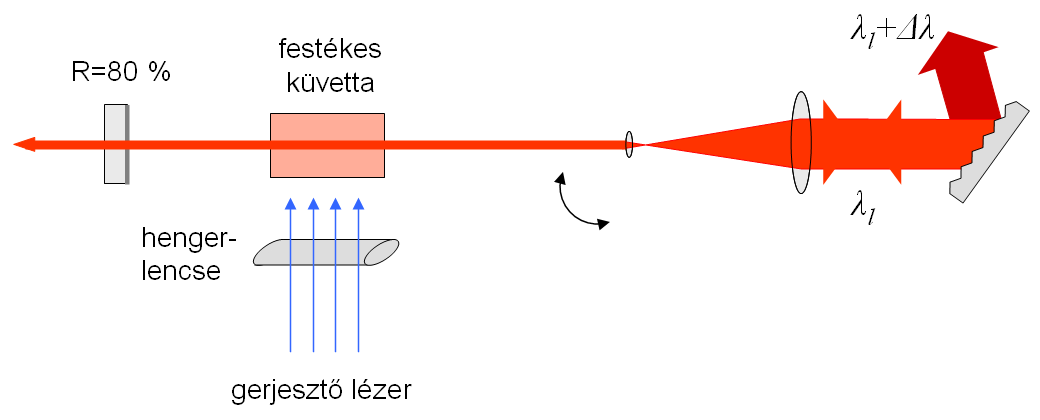
11.7. ábra. Hangolható festéklézer teleszkópikus nyalábtágítóval.
Egy különleges lézertípus, az elosztott visszacsatolású lézer (EVL), ahol a lézerműködéshez szükséges visszacsatolást nem tükrökből álló optikai rezonátorral hozzák létre, hanem a lézer aktív anyagának optikai paramétereit térben periodikusan modulálják [11.4]. A modulált optikai paraméter lehet az aktív anyag törésmutatója, vagy erősítési tényezője, vagy egyszerre mindkettő. A 11.8. ábrán a világos csíkok helyén erős gerjesztés, míg a sötét csíkok helyén gyengébb gerjesztés jön létre. Ez kicsiny Δn törésmutató-változást okoz periodikusan. Mindkét irányban haladhat hullám az aktív anyagon keresztül. Minden határfelületnél egy kis hányaduk visszaverődik. Bár a visszaverődés mértéke kicsiny, de ez sokszor ismétlődik meg az anyagban, a csíksűrűségtől függően. Azon hullámhosszak esetében, melyeknél a visszavert fényhullámok fázishelyesen adódnak össze, az eredő erősítés olyan nagy lehet, hogy lézerként működik.
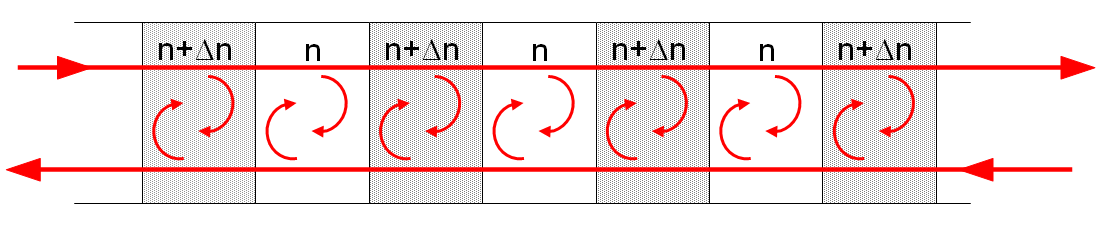
11.8. ábra. Az elosztott visszacsatolású festéklézerben kialakuló törésmutató profil és visszacsatolás.
Az EVL aktív anyaga általában festékoldat vagy félvezető. A továbbiakban az elosztott visszacsatolású festéklézerek (EVFL) működésével foglalkozunk.
Az EVFL-ek működéshez szükséges, térben periodikus struktúrát (amplitudó-fázisrácsot) holográfiai vagy fotolitográfiai úton állítják elő. Míg az amplitudó-fázisrács a statikus EVFL-ekben a lézer működése közben végig jelen van, addig a dinamikus EVFL-eknél a gerjesztő lézernyalábbal előállított interferencia-csíkrendszer hozza létre (11.9. ábra). Ez utóbbi esetben a rács a gerjesztő impulzus hatására jön létre, a festéklézer működése közben változik, végül a gerjesztő impulzus megszűnte után néhány nanoszekundum alatt eltűnik. A dinamikus EVFL-ben a visszacsatolást döntően az erősítési tényező térbeli modulációja okozza.
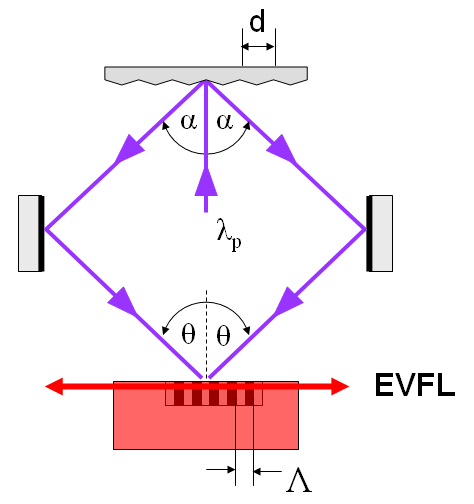
11.9. ábra. Elosztott visszacsatolású festéklézer gerjesztése [11.5].
A 11.9. ábrán a λ p hullámhosszú gerjesztő lézer nyalábja egy reflexiós rácson α szögben diffraktálódik +1. és -1. rendben, melyre teljesül, hogy
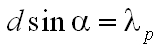 |
. | (11.3) |
A két diffraktált nyaláb a tükrökről visszaverődve a festékes küvettában 2θ szög alatt találkozik, és interferál egymással, melynek eredményeképpen
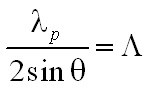 |
(11.4) |
periódusú interferenciacsíkok jönnek létre. Ha α = θ, akkor a csíkok periódusa
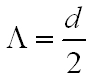 |
. | (11.5) |
Az EVFL központi hullámhossza az első rendű Bragg-feltételből számolható ki, azaz
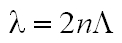 |
, | (11.6) |
ahol n a festékoldat törésmutatója. Ebben az esetben is érvényes, hogy a festéklézer spektrumának van egy véges félértékszélessége, melynek értékét a festékoldatban létrehozott rács periódusaink száma, a rács optikai minősége, valamint a Bragg-feltétel rendje határozza meg. (11.6) egyenlet alapján látható, hogy az EVFL hangolható az interferenciacsíkok periódusának változtatásával.
Az N2-lézerrel gerjesztett dinamikus EVFL csökkenő amplitudóju, pikoszekundumos impulzussorozatot generál. Bizonyos gerjesztési intenzitásnál elérhető, hogy egyes-impulzusok legyenek, melyek közel Gauss-os időbeli lefutásúak [11.5].
Mivel az impulzus üzemű lézer frekvenciában mért Δν spektrális sávszélessége és τ időbeli félértékszélességének szorzata egy állandó érték, ez azt eredményezi, hogy a folytonos üzemű lézerek (11.10. ábra) esetében a kibocsátott lézerfény spektrumának szélessége MHz-es nagyságrendű is lehet.
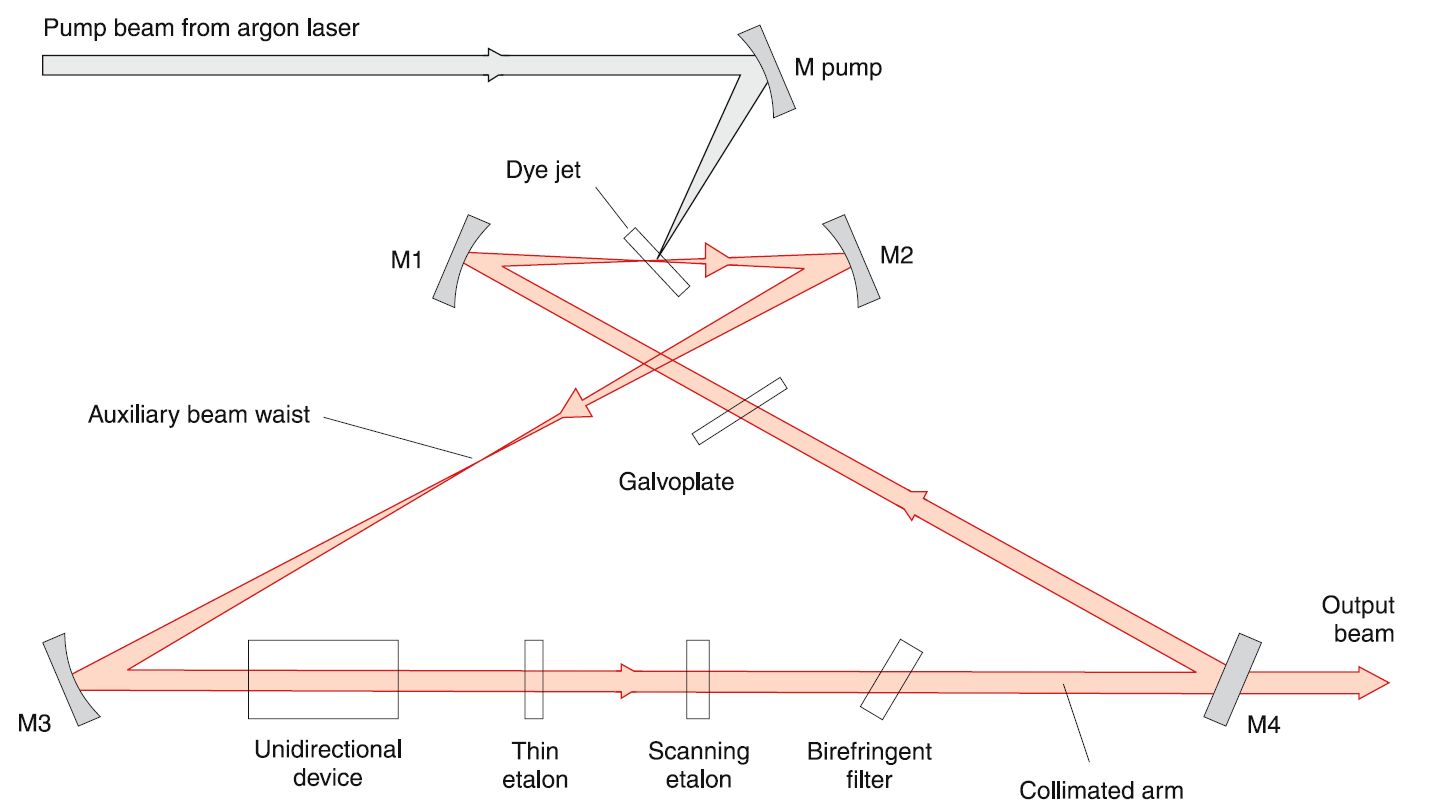
11.10. ábra Folytonos üzemű festéklézer felépítése [11.3].
E lézertípusnál a festékoldatot egy vékony, kb 0,5 mm vastag folyadéksugárban áramoltatjuk, amelyet egy folytonos üzemű argonlézerrel gerjesztünk. A gerjesztő nyalábot az M tükör fókuszálja rá a folyadéksugárra. A lineáris rezonátor felépítésétől eltérően ebben az esetben a négy tükör (M1, M2, M3, M4) egy gyűrűrezonátort alkot. Míg a lineáris rezonátorban egy állóhullámú tér épül fel, addig ennél a lézernél elérik, hogy a gyűrűrezonátorban a hullám egyirányban körbe-körbe jár. Ennek a megoldásnak az előnye, hogy nincsenek módusok a rezonátorban, így az aktív anyag teljes populációinverziós része hozzájárul a lézererősítéshez. Olyan módon kerülhető el a két irányban körülfutó hullám, hogy az egyik irányban nagyobb veszteséget hozunk létre, mint a másikban. Ez elérhető egy optikai egyenirányító eszközzel, például egy kettősen törő kristállyal és egy Faraday rotátorral. A Faraday rotátor az egyik irányból érkező nyaláb polarizációs síkját jobban elforgatja, míg a másik irányból érkezőjét meg éppen visszaforgatja. A rossz polarizációjú nyalábnak az üveg anyagú optikai elemeken való visszaverődésekor a Brewster-törvény miatt nagyobb lesz a reflexiós vesztesége.
A hullámhossz szelekciót ebben az esetben a kettősen törő kristállyal illetve két eltérő bázistávolságú Fabry-Perot etalonnal érjük el. Ha mindkét etalon vastagságát úgy állítjuk be, hogy ugyannál a λ hullámhossznál legyen a transzmissziós csúcs, akkor egymódusú üzemben fog működni a lézer. A két etalont együtt elhangolva a lézer hullámhossza is hangolódik.
Rajzolja fel a festék molekulák tipikus energiaszint diagramját, és jelölje be rajta a sugárzásmentes és sugárzásos átmeneteket!
Melyik festékek emittálnak a 600 nm hullámhosszon?
Milyen optikai elemet kell a rezonátorba behelyezni, hogy hangolni tudjuk a festéklézer hullámhosszát?
Ismertesse az elosztott visszacsatolású festéklézerek (EVFL) működésének elvét!
[11.1] P. P. Sorokin and J. R. Lankard, IBM J. Res. Develop. 10, 162 (1966).
[11.2] F. P. Schäfer, W. Schmidt, J. Volze, Appl. Phys. Lett. 9, 306 (1966).
[11.3] W. Demtröder: Atoms, Molecules and Photons (Springer, 2006)
[11.4] H. Kogelnik, C.V. Shank, Appl. Phys. Lett. 18, 152 (1971)
[11.5] Zs. Bor, A. Müller, IEEE QE-22, 1524 (1986)
Tartalom
Gázok esetén a vonalkiszélesedést okozó mechanizmusok sokkal kevésbé fejtik ki hatásukat, mint a szilárd testeknél vagy a folyadékoknál, ezért az energiaszintek szélessége általában GHz-es vagy annál kisebb. A gázlézerekben jellemzően alkalmazott alacsony nyomáson az ütközések okozta kiszélesedés általában elhanyagolható, a fő mechanizmus az inhomogén kiszélesedést okozó Doppler eltolódás. A széles abszorpciós vonalak hiánya miatt széles spektrumú optikai pumpálás nem megvalósítható, ezért bizonyos esetekben lézeres (pl. dióda lézer) gerjesztést alkalmaznak, de a legelterjedtebb az elektromos pumpálás, melynek során megfelelő intenzitású (folytonos, impulzus vagy rádiófrekvenciás) áramot vezetnek keresztül az aktív közegen. A (jellemzően többlépcsős) gerjesztési folyamat ilyenkor a felgyorsított elektronokkal való ütközés következménye. A gerjesztett atomok több folyamaton keresztül kerülhetnek vissza az alacsonyabb energiaszintekre: i) elektronnal való ütközés során leadhatják energiájuk egy részét (szuper-elasztikus ütközés); ii) rezonancia-közeli ütközés során a gerjesztési energia átadódik a gáz egy alapállapotban levő (ugyanolyan, vagy másik elem) atomjának. A tartály falával való ütközés (iii) szintén a gerjesztett atomok számának csökkenéséhez vezet és figyelembe kell venni (iv) a spontán emissziót is.
Adott áramerősség esetén kialakul egy bizonyos egyensúlyi populáció, azonban a figyelembe veendő folyamatok nagy száma miatt a populációinverzió megvalósítása nehezebb, mint pl. szilárd halmazállapotú közegek esetén. Általánosságban kijelenthető, hogy az inverzió megvalósításához az alábbi két feltételből legalább az egyiknek teljesülnie kell: a lézerátmenet felső szintjére a gerjesztési sebesség nagyobb legyen, mint az alsó szintre és az élettartam a felső szinten nagyobb legyen, mint az alsó szinten. Ez utóbbi feltétel nem teljesülése esetén a lézer csak impulzus-üzemmódban működhet.
A gázlézer típusok száma meglehetősen nagy, a következő felsorolásban ezek közül a jelentősebbeket ismertetjük, a teljesség igénye nélkül.
A He-Ne lézer legelterjedtebb a nemesgáz lézerek (He-Xe, Ar-Xe) közül, emellett az 1,15 μm hullámhosszon működő változata a legelső gázlézer és ugyanakkor a legelső folytonos üzemmódú lézer is volt. Ahogy a neve is mutatja, az erősítő közeget hélium és neon gázkeveréke alkotja. A lézerműködés a Ne energiaszintjei között átmeneten alapul, a He szerepe a gerjesztés hatásfokának a növelése. A leggyakrabban a vörös színű, 632,8 nm-es hullámhosszon használják, egyéb működési hullámhosszak közül jelentősebbek az 543,5 nm, 1,15 μm és a 3,39 μm. Működési termsémája a 12.1. ábrán látható. A He atomok egyik elektronja az 11S (antiparallel spinek) alapállapotból az elektronokkal való ütközés során a 2S (Russel-Saunders jelölés, kiegészítve a főkvantumszámmal) gerjesztett állapotba kerülnek, melynek energiája függ a spinek irányítottságától. A 10 elektronnal rendelkező Ne külső (2p) elektronpályáján 6 db. elektron van, melyek közül az egyik elektronnak a gerjesztett energiaszintjeit jelöli a 3s, 3p, stb. (Paschen jelölés). A 2p pályán maradt 5 elektronnal való kölcsönhatás miatt a gerjesztett s energiaszintek 4 alszintre, a p szintek pedig 10 alszintre hasadnak. Az ábrán látható, hogy a He atom 21S és 23S szintjeinek energiája közel megegyezik a Ne 4s és 5s szintjeivel ezért rezonancia-közeli ütközéssel a He átadhatja gerjesztési energiáját a neon atomoknak. A Ne atomok gerjesztése történhet közvetlen elektron ütközéssel is, azonban ennek hatáskeresztmetszete jóval kisebb. Mivel a foton kibocsátással járó s → p átmenet megengedett, és az s szintek élettartama körülbelül egy nagyságrenddel nagyobb, mint a p szinteké, adottak a feltételek az átmenet lézerműködésre való felhasználásához. A fontosabb lézerátmenetek a 12.1. ábrán láthatók. A lézer működési hullámhossza könnyedén kiválasztható hullámhossz-szelektív dielektrikum tükrök alkalmazásával.
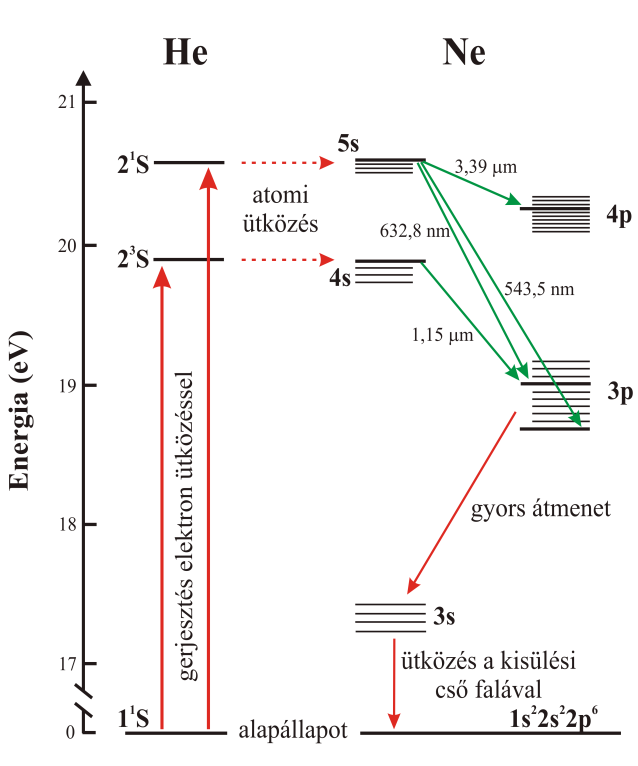
12.1. ábra. A He-Ne lézer releváns energiaszintjei és a főbb lézer-átmenetek.
A He-Ne lézer felépítésének elvi vázlata a 12.2. ábrán látható. A gázkeverék egy kvarc tartályban található, a lézercső végablakainak Brewster-szögű kialakításával polarizált lézerműködés érhető el. A gázkisülést a cső végei közelében elhelyezkedő egy jellemzően gyűrűszerű anód és egy (általában nagyobb felületű, a pozitív ionok bombázásának jobban ellenálló) katód között hozzák létre úgy, hogy a kisülés csak egy, a gáztartályban hosszanti irányban elhelyezkedő kapilláris cső belsejére korlátozódjon. A gázkisülés gerjeszthető mind egyenárammal, mind pedig rádiófrekvenciával, melynek periódusa kisebb, mint a gerjesztett állapot élettartama (~100 ns). A He-Ne lézer egyik sajátossága, hogy a kisülés áramának növelésével nem nő monoton módon a kimeneti teljesítmény, hanem elér egy maximumot (~10 mA áramerősségnél), majd csökkenni kezd. Ennek oka, hogy megnő a jelentősége a gerjesztett He atomok elektronokkal való szuper-elasztikus ütközésének, ami a gerjesztett populáció növekedése ellen hat. Optimális elektron-hőmérsékleti (elektron-sebesség) és diffrakciós megfontolások alapján további optimális működési paraméterek: i) 1-2 mbar össznyomás, ii) He:Ne parciális nyomás arány ~5:1 a 632,8 nm és ~9:1 az 1,15 μm hullámhosszakon. ii) kapilláris átmérő ~2-5 mm. A kis erősítési tényező miatt nagy reflexiójú rezonátor-tükrökre van szükség, a kicsatolási arány kisebb, mint 2%.
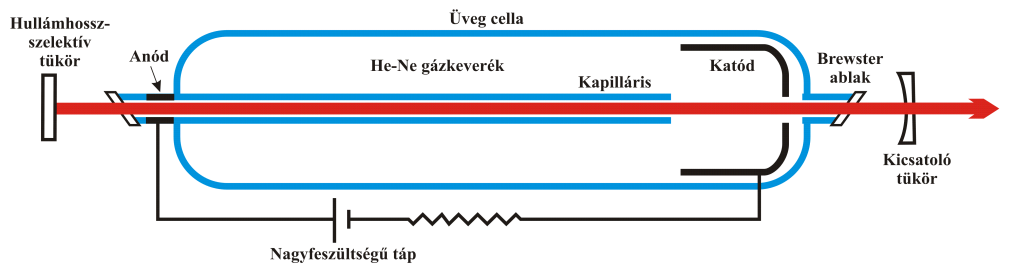
12.2. ábra. A He-Ne lézer felépítése.
A He-Ne lézerek kis kimeneti teljesítménnyel rendelkeznek: 0,5 m csőhossz esetén 632,8 nm-en ez kevesebb, mint 10 mW, míg a többi hullámhossz esetén egy nagyságrenddel is kevesebb lehet. A hatásfokuk rendkívül alacsony, kisebb, mint 0,1%. Ennek egyik oka a nagyon alacsony kvantumhatásfok: míg a gerjesztési energia ~20 eV, a kibocsátott foton energiája ~2eV. A Doppler kiszélesedett lézerátmenet kis sávszélessége (~1,5 GH) miatt megfelelően rövid (<15-20 cm) hemiszférikus rezonátor alkalmazásával egymódusú TEM00 működés érhető el. A rezonátor nagy foton-élettartama miatt az oszcilláló módus sávszélessége ~10-3 nm, vagy annál kisebb, ami nagy koherenciahosszt eredményez. A középponti hullámhossz stabilizálása piezoelektromos mozgatású tükrökkel valósítható meg. Jód abszorpciós gázcella (referenciaként) és nagyhosszúságú Fabry-Perot interferométer alkalmazásával akár 10-11 relatív hullámhossz-stabilitás is elérhető.
Alkalmazási területeinek egy részéről (pl. sejtszámlálás, célzó-lézer, vonalkód leolvasók) az olcsó félvezető lézerek kiszorítják a He-Ne lézereket, azonban a spektrális jellemzők szempontjából igényes területeken (nagy pontosságú interferometria, távolságmérés, holográfia, spektroszkópia) továbbra is alkalmazzák
A fém-gőz lézerek közül (Pb, Au, Mn, Ba) a legismertebb. Háromszintes termséma alapján működik (12.3. ábra). Alapállapotban ( 2S1/2 ) a rézatom 3d 104s1 konfigurációval rendelkezik. A lézerátmenet felső ( 2P ) energiaszintje a külső 4s pályán levő elektronnak a 4p pályára való gerjesztésével jön létre, az alsó ( 2D ) szintet pedig a 3d pályáról a 4s pályára gerjesztett elektronhoz tartozó 3d 94s2 konfiguráció képezi. Az alszintek figyelembevételével két különböző hullámhosszú lézer-átmenettel rendelkezik: egy sárga színű 578 nm-es és zöld színű 510 nm-es hullámhosszal. Az 1500 ºC hőmérsékleten kialakuló ~0,1 mbar parciális nyomású rézgőzt elektron-ütközéssel gerjesztik. A felső lézerszintre hatékonyabb a gerjesztés, így a populációinverzió megvalósítható, azonban az alsó szint élettartama nagy, ezért a lézer-átmenet önkioltó, csak impulzusüzemű működés lehetséges.
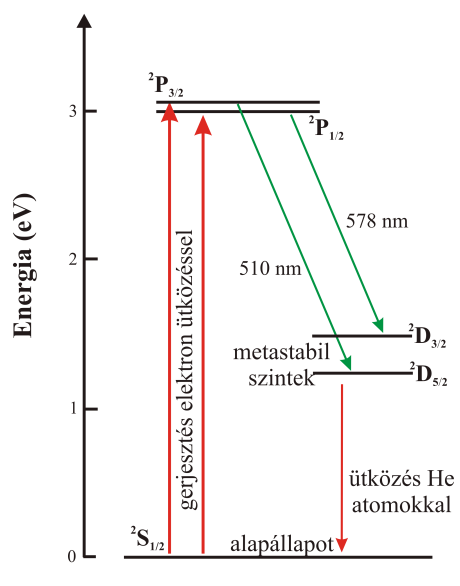
12.3. ábra. A rézgőz lézer működésében résztvevő energiaszintek.
A lézer felépítésének vázlata a 12.4. ábrán látható. A rézgőz egy alacsony nyomású kamrában elhelyezett, hőszigetelt alumíniumoxid cső belsejében található, itt jön létre a kisülés a cső két végén található elektróda között. A működési hőmérsékletet a kisülést gerjesztő áram-impulzusok által keltett hő biztosítja. A néhányszor tíz mbar nyomású He puffer-gáznak kettős szerepe van: szuper-elasztikus ütközéssel segíti az alsó lézerszint kiürülését és gátolja a rézatomoknak a tartály hideg falai irányába történő diffúzióját.
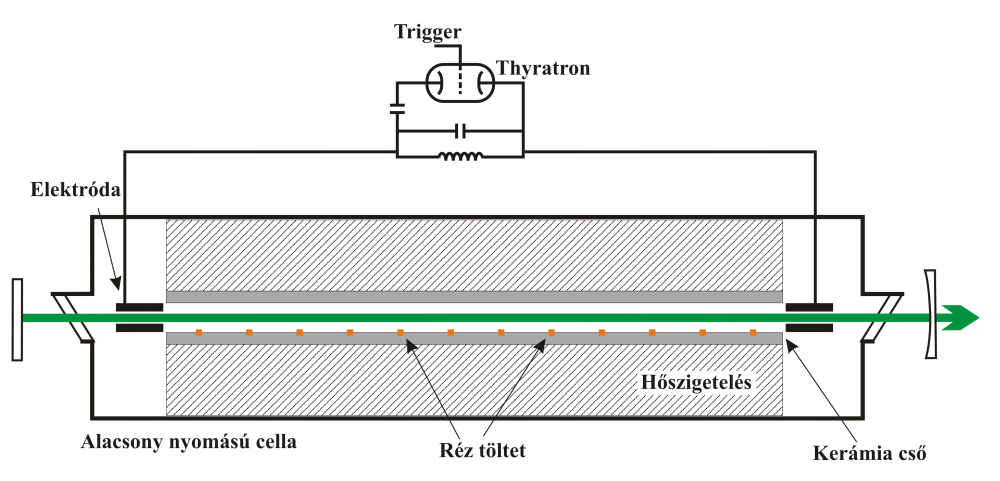
12.4. ábra. A rézgőz lézer felépítése.
A rézgőz lézerek hatásfoka néhány százalékos. Átlagteljesítményük 100-200 W, ismétlési frekvenciájuk 10-20 kHz, az impulzushossz ~30 ns, a csúcsteljesítmény pedig ~1MW körüli. A működési hullámhosszt a rezonátorba épített diszperziós elemmel lehet beállítani (lásd 6.4 fejezet). Alkalmazhatók festéklézerek gerjesztésére, gyorsfényképezésre, mikromegmunkálásra, de urán-izotóp szeparációra is.
Annak ellenére, hogy a lézerműködés megvalósítására alkalmas erősítő közegnek legelőször az alkáli fémek gőzeit javasolták, keskeny sávszélességű és elegendően nagy teljesítményű optikai pumpáló eszközök hiányában a századfordulóig nem tudtak megfelelő hatékonysággal rendelkező alkáli lézereket építeni. Az alkáli fémek (Li, Na, K, Rb és Cs) külső elektronhéján 1 darab s elektron található, ezért a gerjesztett energiaszintek relatíve egyszerű szerkezetűek. A keskeny pumpálási sávszélesség igényt jól szemlélteti a 12.5. ábra, melyen a Rb atomok lézerműködésben szerepet játszó energiaszintjei láthatók. Alapállapotban az atom a 2S1/2 szinten van, az első és második gerjesztett szintek ( 2P1/2 és 2P3/2 ) között csak a spin-pálya kölcsönhatásból származó kis energiakülönbség van. A gerjesztett szintek között megközelítőleg termális egyensúly alakul ki, ezért a lézer kvázi-kétszintes rendszernek tekinthető. Mivel a pumpáló- és a lézer hullámhossz csak kismértékben tér el egymástól, nagy a lézerműködés kvantum-hatásfoka.
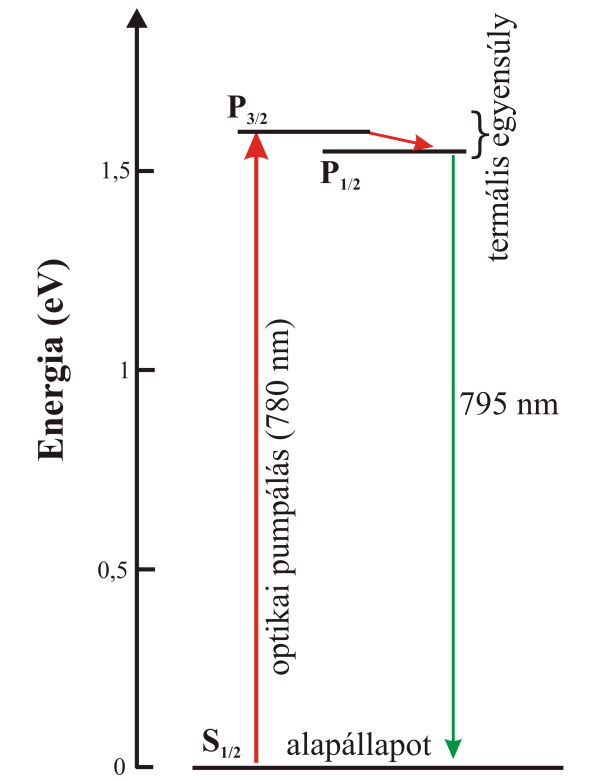
12.5. ábra. A Rb-gőz lézer energiaszintjei.
Az alkáli fém alacsony parciális nyomású gőzét egy melegített (~100-150 ºC) gázcella tartalmazza (12.6. ábra), puffergáznak néhány száz millibar nyomású He-ot és/vagy alacsony molekulatömegű szénhidrogén gázt (etán, metán) alkalmaznak. A puffergáz szerepe kettős: kiszélesíti a gerjesztési abszorpciós vonalat és az ütközések által elősegíti a P1/2 és P3/2 szintek közötti termikus egyensúly kialakulását és ezáltal a felső lézerszint töltődését. Pumpálásra longitudinális, vagy transzverzáliszális elrendezésben titán-zafír, alexandrit vagy dióda lézereket alkalmaznak.
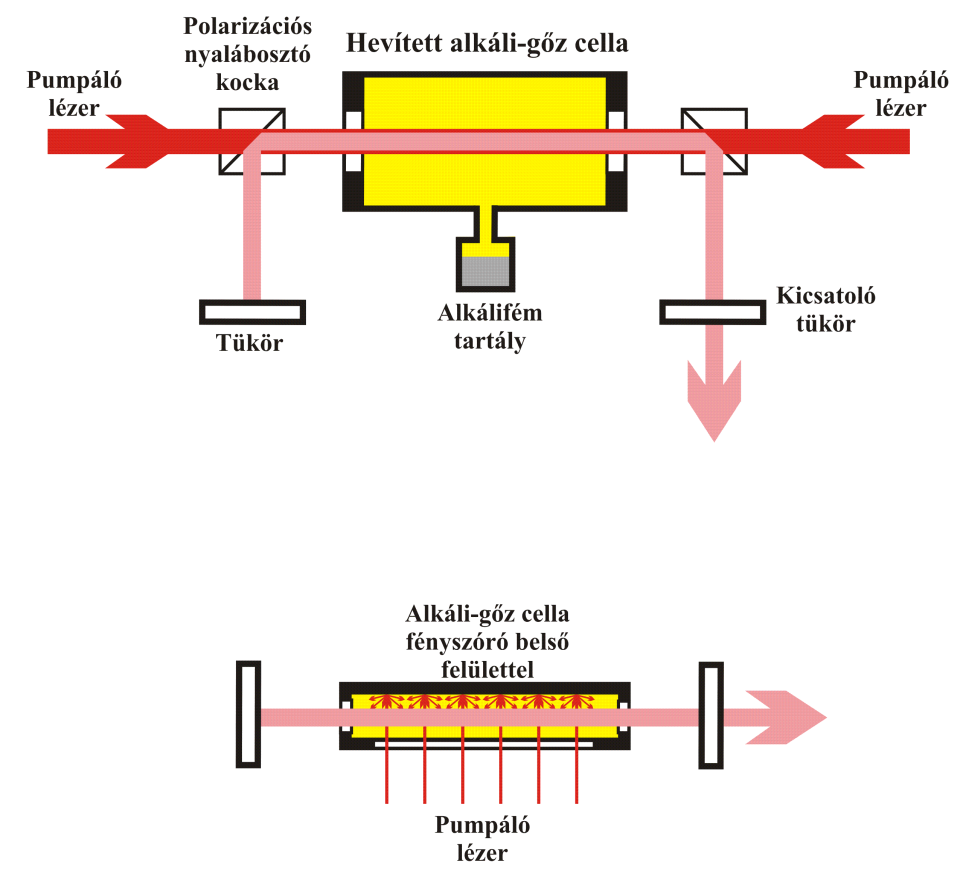
12.6. ábra. Alkáli-gőz lézerek longitudinális és transzverzális pumpálási elrendezései.
Az alkáli lézerek hullámhossza a közeli infravörös tartományban van (K: 770 nm, Rb: 795 nm, Cs: 895 nm), az ütközési/nyomás kiszélesedés homogén volta miatt az egymódusú (TEM00 ) lézerműködés könnyen megvalósítható. A pumpálástól függően folytonos, vagy impulzusüzemű működés is lehetséges. A kezdeti néhány mW folytonos teljesítményről napjaikra (diódalézer pumpálással) eljutottak a kW-os teljesítményig, a jelenleg a 100 kW-MW-os tartomány elérését célzó fejlesztések folynak. Az extrém nagy teljesítmények elérését a nagy (~60%) optikai konverziós- és akár ~30% teljes (elektromos → optikai) hatásfok teheti lehetővé. Nagyteljesítményű lézerként ipari és katonai felhasználásokra szánják.
Pozitív ionok esetén a hiányzó elektron miatt az atommag töltése kevésbé van leárnyékolva, ezért a semleges atomokhoz képest az energiaszintek átskálázódnak, nagyobb távolságra kerülnek egymástól. Ennek következtében, míg a semleges-atom lézerek az infravörös és látható hullámhosszakon üzemeltek, a ion lézerek működési tartománya a nagyobb foton energiák felé, a látható és ultraibolya tartományba tolódik át.
Az Ar+ lézer a nemesgáz-ion lézerek legjelentősebb képviselője. A lézerműködés szempontjából lényeges energiaszintek a 12.7. ábrán láthatók. Az Ar atom külső 3p pályáján 6 db. elektron van, melyből az egyiket eltávolítva alapállapotú Ar+ iont kapunk. A maradék 5 elektronból valamelyiket a 4s vagy 4p szintekre gerjesztve kapjuk meg a lézerműködésben résztvevő két gerjesztett állapotot. A 3p szinten maradt elektronokkal való kölcsönhatás következtében ezen szintek több alszintre hasadnak fel. Az Ar atomok elektron-ütközéses pumpálása két, vagy három lépésben játszódik le. Az első ütközés létrehozza az alapállapotú iont, innen történik a további gerjesztés. Ez utóbbi háromféleképpen valósulhat meg: a) közvetlen gerjesztés a 4p szintre, b) gerjesztés egy közbenső, metastabil állapotba, ahonnan tovább gerjesztődik a 4p szintre és c) gerjesztés egy magasabb energiaszintre, ahonnan relaxációval visszaesik a 4p szintre. A 4s szintre való gerjesztés hasonlóan játszódik le, azonban ennek az élettartama körülbelül a tized része a 4p szint élettartamának. Ennek következtében a populációinverzió megvalósíthatóságának a feltétele adott, azonban a megfelelő mértékű inverzió eléréséhez a kétlépcsős gerjesztés miatt nagy áramsűrűség (~kA/cm2) szükséges.
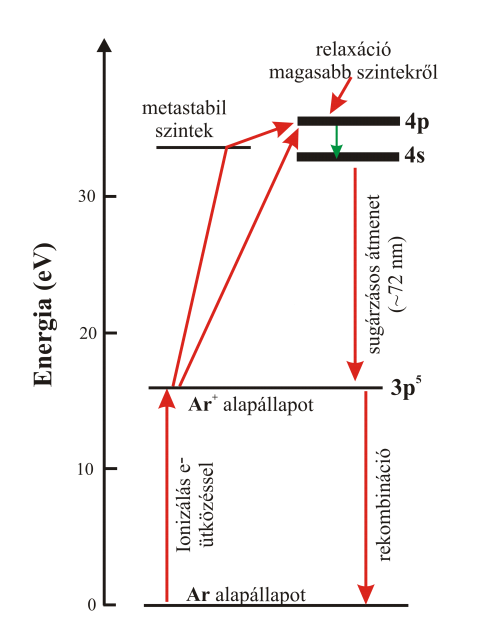
12.7. ábra. Az argon-ion lézer energiaszintjei.
A lézer felépítésének vázlata 12.8. ábrán látható. A kis nyomású (~0,5 mbar) Ar gáz egy kerámiacsőben található, a kisülés a cső tengelyében, volfrám apertúrák által meghatározott kis átmérőjű (~2 mm) térrészben jön léte. A gáz magas hőmérséklete (~3000 ºC) miatt a kerámiacsövet vízárammal hűtik. A katód közelében rekombinálódó atomok a volfrám korongokban létrehozott furatokon keresztül diffúzióval jutnak vissza az anód felé. Nagyobb lézerteljesítmények esetén (>1W) a csőben mágneses teret hoznak létre, mellyel az elektronokat a tengely körül spirális pályán lehet tartani, csökkentve a fal felé történő elektron-diffúziót és nagyobb pumpálási sebességet eredményezve.
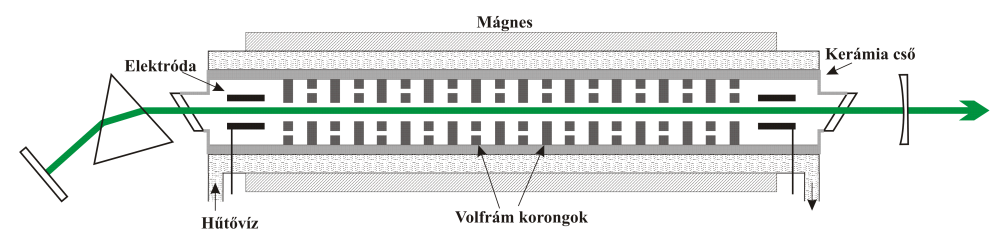
12.8. ábra. Az argon-ion lézer felépítése.
A kis átmérőjű apertúrák miatt a lézer TEM00 módusban működik. A felhasadt energiaszintek következtében több lézerátmenettel rendelkezik, a legintenzívebbek a 351, 488 és 514,5 nm hullámhosszúságúak. Hatásfokuk alacsony (<0,1%), kimeneti teljesítményűk kiviteltől függően ~0,1-20 W. Néhány alkalmazási területük: lézergerjesztés, litográfia, diabetikus retinopátia kezelés, stb.
A legismertebb a fém-ion lézerek (Se, Sn, Pb, Zn) közül. A lézerátmenet a Cd atomok szolgáltatják, a gerjesztésüket a He atomok biztosítják az ún. Penning ionizáció által. A Penning ionizáció egy nem-rezonáns ütközés, melynek során az egyik gerjesztett atom átadja az energiáját a másik atomnak: ionizálja azt, míg az energiafelesleget a kilépő elektron viszi el mozgási energia formájában. A He és Cd energiaszintjei a 12.9. ábrán láthatók. Az elektronütköztetéssel a 21S és 23S szintre gerjesztett He atomok a Cd atomokkal ütközve ezeket ionizálják úgy, hogy az ionok eleve a 2D és 2P gerjesztett állapotba kerülnek. A magasabb energiával rendelkező 2D szintre a gerjesztés körülbelül háromszor nagyobb valószínűséggel megy végbe, mint a 2P szint esetén, emellett a 2D szint élettartama százszorosa a 2P szint ~1 ns-os élettartamának. Ennek következtében a 2P és 2D szint között poulációinverzió alakul ki. A rendszer két lézerátmenettel rendelkezik: 2D3/2 → 2P1/2 és 2D5/2 → 2P3/2, melyek 325 nm-es (ultraibolya) és 416 nm-es (kék) fotonokat eredményeznek.
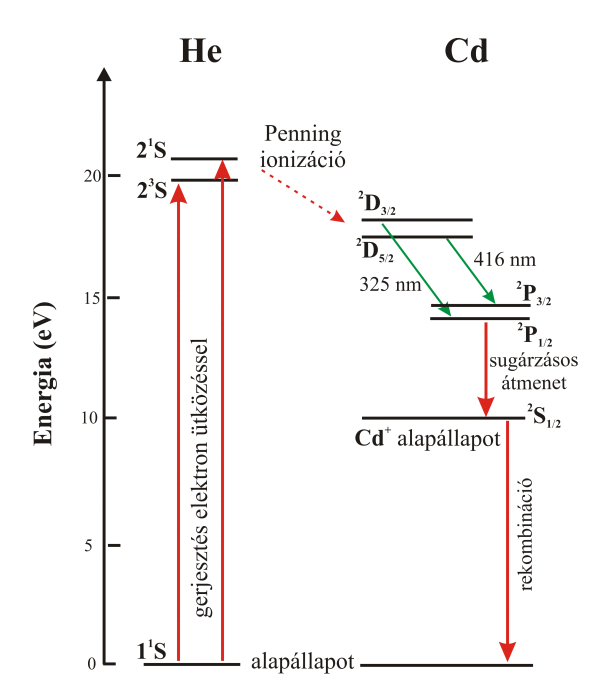
12.9. ábra. Energiaszintek a He-Cd lézerben.
A kisülési csövet 2-4 mbar nyomású He-mal töltik fel, a működéshez szükséges fém gőzt (~10-2 mbar parciális nyomással) egy 250 ºC-ra hevített, az anód közelében elhelyezkedő Cd tartály biztosítja. A Cd atomok a katód közelében rekombinálódnak és kondenzálódnak, ezért a Cd tartály tartalma folyamatosan csökken (~1g/1000h).
A lézer folytonos üzemű, hatásfoka - hasonlóan az Ar+ lézeréhez - alacsony, legnagyobb kimeneti teljesítménye ~100-200 mW. Felhasználható litográfiára, fluoreszcencia spektroszkópiára, citometriára, stb.
A molekulák energiaszint struktúrája jóval összetettebb, mint a semleges atomoké vagy akár ionoké. Az egyes elektronállapothoz különböző rezgési energiaszintek, melyek mindegyikéhez további rotációs energiaszintek tartoznak. Annak függvényében, hogy a lézerátmenet milyen energiaszintek között történik, három típusba sorolhatók:
i) A rotációs lézerek az alap elektronállapothoz tartozó valamely vibrációs szintnek két rotációs nívója közötti átmeneten alapulnak. Mivel a rotációs szintek közötti energiakülönbség alacsony, ezen lézerek hullámhossza a távoli infravörös tartományban van (pl. CH2F lézer, 496 μm), nem képviseltetik magunkat az elterjedtebb lézertípusok között.
ii) A vibrációs-rotációs lézerek az alap elektronállapothoz tartozó vibrációs szintek közötti átmenetet használják, a közép- és távoli infravörös tartományon működnek. Jelentősebb képviselőjük a CO2, CO lézerek, valamint a pumpálásra kémiai reakció energiáját használó HF (kémiai) lézer.
iii) A vibronikus lézerek különböző elektronállapotok vibrációs szintjei közötti átmenetre épülnek, jellemzően ultraibolya tartományban működnek. A kategória legjelentősebb tagja a nitrogén lézer. Tulajdonképpen ugyanide sorolható a lézereknek egy speciális csoportja: az excimer lézerek Ezen lézerekben az átmenet nem két kötött állapot között megy végbe, hanem az alsó lézerszint egy taszító állapot lesz, ahol a molekula disszociál.
A CO2 lézer napjaink egyik legelterjedtebb és egyik legnagyobb teljesítményű lézertípusa. A lézer oszcilláció a CO2 molekula két vibrációs szintje közötti átmeneten alapul, azonban a lézerműködéshez szükség van N2 és He gázokra is. Az O-C-O molekulaszerkezetnek köszönhetően háromféle alap rezgéstípussal rendelkezik: szimmetrikus rezgés, deformációs rezgés és aszimmetrikus rezgés. A rezgési energiaszinteket ezen rezgéstípusokhoz tartozó kvantumszámokból alkotott szám-hármassal jelölhetjük. A 12.10. ábrán láthatók a CO2 és N2 molekuláknak a lézerműködés szempontjából fontos vibrációs energiaszintjei, a rotációs szintek részletezésétől eltekintünk. A CO2 molekulát pumpálással a (000) alapállapotból a (001) aszimmetrikus rezgési energiaszintre gerjesztik. A hatékony pumpálás különböző utakon valósulhat meg. a) Közvetlen elektron ütközéssel gerjeszthető a (000) → (001) átmenet, emellett bekövetkezhet a gerjesztés valamely magasabb (00n) szintre is, ahonnan a molekula gyorsan relaxálódik miközben rezonancia-közeli ütközéssel egy-egy rezgési energiakvantumot átad egy másik CO2 molekulának, (001) gerjesztett állapotba hozva azt. b) A rezonancia-közeli ütközés a metastabil első rezgési szintre elektron-ütközéssel gerjesztett N2 molekulával szintén hatékonyan hozzájárul a populáció növeléshez a (001) szinten. A lézerműködés a (001) → (100), valamint a (001) → (020) szintek között jöhet létre, melyekhez rendre a 10,6 μm és 9,6 μm hullámhosszak tartoznak. Ütközéses és sugárzással járó átmenetek során az alsó lézerszintről a molekulák rövid idő alatt a (010) szintre relaxálódnak. A (010) szintek telítődését (és a lézerműködés megszűnését) He molekulákkal való elasztikus ütköztetéssel gátolhatjuk meg, emellett a hélium jelentős szerepet tölt be a CO2 molekulák hűtésében is. A lézer-átmenetek vonalszélessége kicsi (~50 MHz), melyet általában a Doppler kiszélesedés dominál. A nagyobb nyomásokon működő változatokban (>100 mbar) a kiszélesedés fő oka molekulák közötti ütközés.
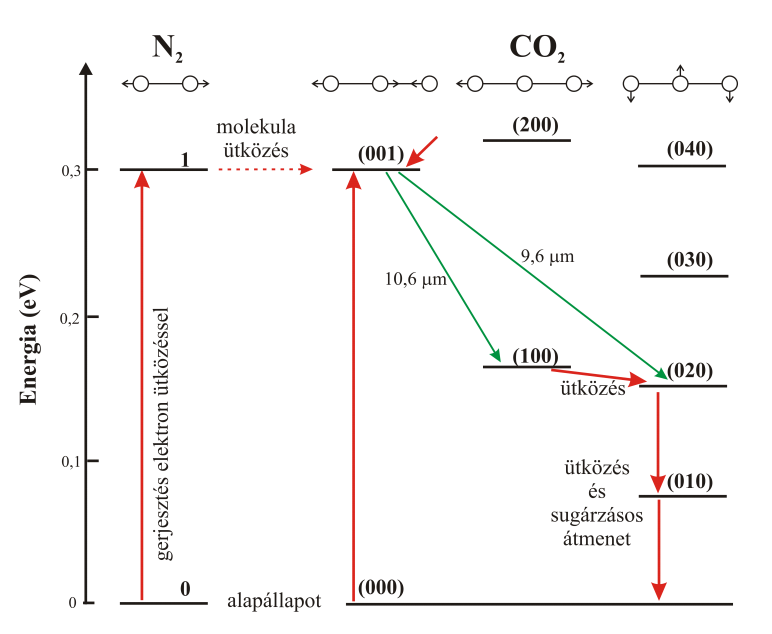
12.10. ábra. A CO2 lézer energiaszint struktúrája.
A CO2 lézerek felépítése/kialakítása nagymértékben függ a kiadott teljesítménytől (1 W - 100 kW). Jellemzőjük a TEM00 transzverzális alapmódus és a keskeny vonalszélesség miatt az egyetlen longitudinális módusban való működés. Hatásfokuk elérheti a nagyon jónak tekinthető 20%-ot. A folyamatos hűtést igénylő kisülési cső általában 50 cm-nél hosszabb, de elérheti a több métert is. A gázösszetétel aránya CO2 : N2 : He ≈ 1 : 4 : 5, a teljes gáznyomás az alacsonytól (~10 mbar) az atmoszférikus tartományig terjedhet (nagy teljesítmények esetén). A gáz melegedése miatt folyamatos áramoltatás szükséges, ami lehet longitudinális vagy transzverzális irányú is. A kisülés gerjeszthető egyenárammal, impulzusokkal és radiófrekvenciával is, az iránya úgyszintén lehet longitudinális, vagy transzverzális.
Az első CO2 lézerek nyitott gázrendszerrel működtek, folyamatos longitudinális gáz-áramoltatással és longitudinális gerjesztéssel (12.11. ábra). Az ilyen lézerelrendezés napjainkban is a hobbi lézerkészítők egyik kedvelt típusa. A folytonos gázcsere a melegedés mellett a kisülésben keletkező nagy számú CO molekula miatt volt szükséges. A későbbiekben a CO felhalmozódását sikerült kiküszöbölni kis mennyiségű (~1%) vízgőznek a gázkeverékhez adásával. Ezzel lehetővé vált hosszú élettartamú zárt rendszerű, könnyen kezelhető lézerek kialakítására. Az ilyen, zárt rendszerű cw lézerek maximális teljesítménye 100 W körüli.
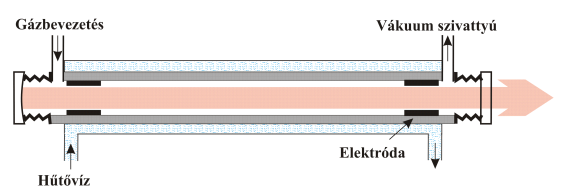
12.11. ábra. Longitudinális áramoltatású és gerjesztésű CO2 lézer felépítése.
A longitudinális áramlási sebesség jelentős növelésével (~50 m/s) és transzverzális gerjesztés alkalmazásával kilowattos cw teljesítmény érhető el. A transzverzális gázáramoltatás (12.12. ábra) lehetővé tette nagyobb gáznyomás (100 mbar) és nagyobb pumpáló áramerősség alkalmazását és többször 10 kW-os teljesítményű lézerek megépítését.
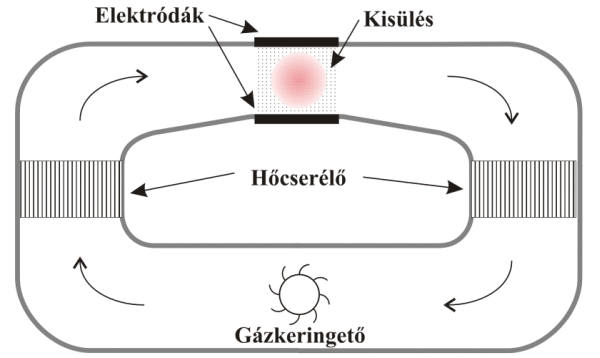
12.12. ábra. Transzverzális áramoltatású és gerjesztésű CO2 lézer keresztmetszeti vázlata.
A transzverzális gerjesztésű, atmoszférikushoz közeli nyomáson üzemelő TEA (Transversely Excited, Atmospheric pressure) CO2 lézer impulzus üzemmódú. A gázt elő-ionizálják, a gerjesztést pedig egy kondenzátor kisütésével valósítják meg. Átlagteljesítménye ~500 W, ismétlési frekvenciája ~50 Hz, az impulzushossz ~100 ns, míg a csúcsteljesítmény MW körüli.
A CO2 lézerek legnagyobb teljesítményű változata gáz-dinamikus pumpálási elven működik. A működéshez szükséges nagy nyomású (~10 bar) és magas hőmérsékletű (~1000 ºC) CO2-t megfelelő üzemanyag elégetéséből nyerik. A magas hőmérséklet miatt megnő a gerjesztett állapotok betöltöttsége, majd az egy fúvókán áthaladó és adiabatikus kitágulást szenvedő gázban megindul a relaxáció. Mivel az alsóbb gerjesztett állapotok élettartama kisebb, az alsó energiaszint hamarabb kiürül, mint a felette levők és kialakul a populáció inverzió. Az ilyen lézerrel elérhető 100 kW folytonos lézerteljesítmény.
A szén-dioxid lézerek alkalmazási területe meglehetősen széles. Alkalmazzák az infravörös spektroszkópiában (~1 W), sebészetben (lézerszike, ~50 W), iparban (fémek fúrása, vágása, párologtatás, ~kW).
A N2 molekula energiaszint sémája a 12.13. ábrán látható. Az alapállapotban levő molekula elektronütköztetéssel gerjeszthető a B és C elektronállapotokba. A B szintre való gerjesztésnek kissebb a hatáskeresztmetszete, azonban a B szint élettartama sokkal nagyobb, mint a C szintté (alacsony nyomásokon 10 µs és 40 ns). Nyilvánvaló, hogy folytonos lézerműködés nem megvalósítható, az impulzusüzemű működéshez pedig 40 ns-nál rövidebb ideig tartó gerjesztés szükséges. A legerősebb lézer-átmenet az C szint 1-es vibrációs szintje és a B szint alap (0-ás) vibrációs szintje között van 337,1 nm UV hullámhosszal. A B szintről a molekulák a metastabil A állapotba kerülnek, ahol a hosszú (~1 s) élettartam miatt felhalmozódnak.
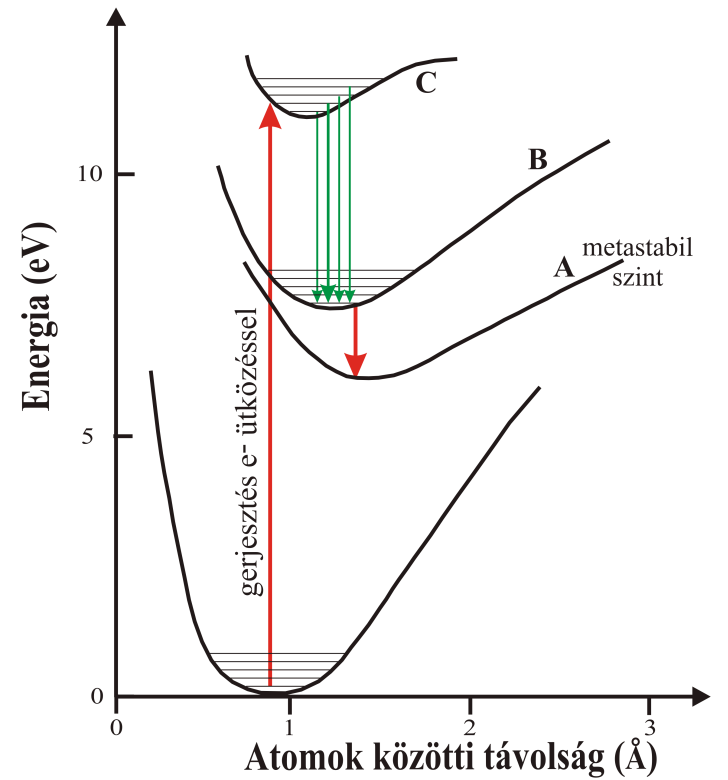
12.13. ábra. A N2 molekula különböző elektronállapotaihoz tartozó potenciálgörbék.
A nitrogén lézer gerjesztése transzverzális kisüléssel történik, az elektródák közötti távolság ~1 cm. A metastabil A energiaszinten való populáció-felhalmozódás miatt zárt rendszerben maximum néhányszor tíz Hz ismétlési frekvencia érhető el. A TEA lézer ~50 mbar N2 és 950 mbar He keverékkel üzemel, de vannak tiszta nitrogénnel üzemelő változatok is. Ez utóbbiak lehetnek alacsony (néhányszor 10 mbar) vagy akár magas (1 bar) N2 nyomáson működik. Nagy nitrogéntartalma (78%) miatt a lézerműködés normál levegőn is megvalósítható, megfelelő nagyfeszültségű forrás birtokában egy demonstrációs célú N2 lézer könnyen összeállítható. A gáznyomás nagymértékben befolyásolja lézerszintek élettartamát ezért a lézerimpulzus időtartama is változik: alacsony nyomáson elérheti a 20-30 ns-ot, atmoszférikus nyomás alkalmazásával 100 ps-ig is lecsökkenthető. A lézercső hossza néhányszor 10 cm, a nagy erősítési tényező miatt a lézer rezonátor tükrök nélkül is működőképes, ezáltal a lézerkimenet tulajdonképpen az erősített spontán emisszió (ASE) képezi, melynek spektrális szélessége nagy (~0.1 nm), a koherencia hossza pedig nagyon kicsi (<1 mm). A hatásfoka alacsony, általában <1%, az impulzusenergia µJ-mJ tartományban van, a maximális ismétlési frekvencia ~1 kHz (áramoltatás és hűtés függő). Rövid hullámhossza miatt főleg festéklézerek gerjesztésére és fluoreszcencia keltésre alkalmazzák.
Az excimer lézerek a molekuláris gázlézerek egy olyan csoportját alkotják, ahol a lézerműködésben olyan kétatomos molekula vesz részt, amely csak gerjesztett állapotban stabil (excimer=excited dimer). A 12.14. ábra az excimer molekulákra jellemző potenciális energia görbéket mutatja. Látható, hogy az alapállapot taszító jellegű, ezért a gerjesztés megszűnésekor a molekula azonnal (ps időskálán) disszociál. Mivel az elektronállapotok közötti energiakülönbség nagy, az excimer lézerek is ultraibolya tartományban sugároznak.
Az első ilyen típusú lézer Xe2 dimeren (172 nm), míg a napjainkban elterjedtebb változatok egy nemesgáz (Ar, Kr, Xe) és egy halogén (F, Cl) atomból álló gerjesztett molekulán alapulnak, ezért ezekre a lézerekre az exciplex (excited complex) terminológia használata lenne helyes. A gerjesztett nemesgáz-halid molekulák egy elektronütközéssel gerjesztett nemesgáz atom és egy alapállapotú halogén atom reakciójából jönnek létre. A gerjesztett nemesgáz molekulák kémiai viselkedése az alkáli fémekéhez hasonló, ezért a létrejövő kötés ionos jellegű lesz. A gerjesztett molekula kialakulásának egy másik módja, hogy a kisülésben kialakuló negatív halogén ion és pozitív nemesgáz ion között jön létre a kötés. Ez utóbbi reakcióhoz (az energia és impulzus-megmaradás törvénye alapján) szükség van egy harmadik összetevőre is, melynek szerepét általában a He és/vagy Ne puffergáz tölti be.
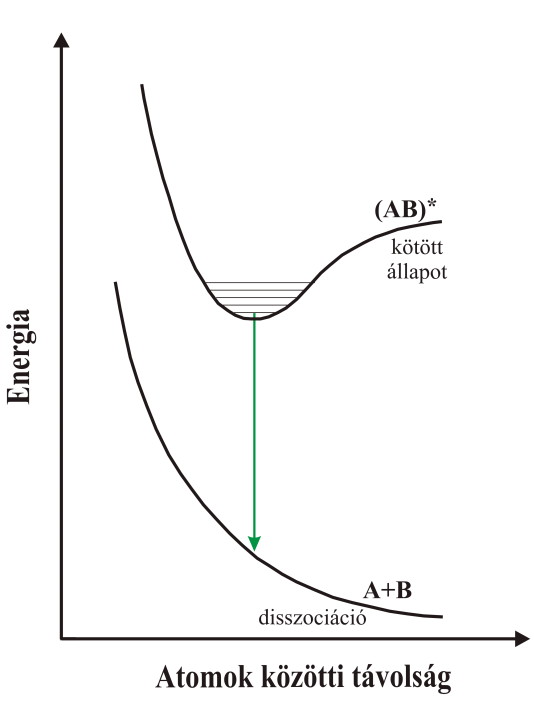
12.14. ábra. Az excimer molekula különböző elektronállapotaihoz tartozó potenciálgörbék.
Az aktív gázok nyomása ~100 mbar-os tartományban van, a gázkeverék legjelentősebb részét a puffergáz teszi ki és a teljes nyomás meghaladhatja a 2 bar-t. A lézercső hossza ~ 1m, gerjesztésre gyors (~10 ns) transzverzális kisülést alkalmaznak (TEA lézer). A nagy erősítés miatt a N2 lézerhez hasonlóan az erősített spontán emisszió dominál, ami nagy impulzusenergiát és gyenge koherencia tulajdonságokat eredményez. Az impulzusenergia ~1J nagyságú, az impulzushossz ~10-30 ns, a maximális ismétlési frekvencia a kHz-es tartományban van. Hatásfokuk elérheti a 4%-ot is. Az excimer lézerek jellemzője, hogy időszakos gázcserét igényelnek és általában a gázkeverék változtatásával különböző hullámhosszakon működtethetők. A fontosabb típusok: XeF (353 nm), XeCl (308 nm), KrF (248 nm), ArF (193 nm). Mivel a megfelelően korrózióálló excimer lézerek működtethetők fluor gáztöltéssel is, az F2 lézert (157 nm) szintén az excimerek lézerek csoportjába szokták sorolni annak ellenére, hogy nem excimer molekuláról van szó.
A fotonok nagy energiájának és az UV tartományra jellemző nagy abszorpciónak köszönhetően az excimer lézerek alkalmasak szerves anyagok és biológiai szövetek hőhatás mentes elpárologtatására (abláció). Felhasználhatók festéklézerek gerjesztésére, anyagmegmunkálásra, de alkalmazzák az orvostudományban is (pl. refraktív szemsebészet). Az UV lézerfény fotokémiai hatását és jó leképezhetőségét használják fel a chipgyártásban az excimer lézeres fotolitográfia során. Az ilyen rendszerekben a kezdetekben alkalmazott KrF-ot felváltották az ArF lézerek, a kisebb elérhető vonalszélesség biztosító F2 lézerek elterjedését gátolja, hogy a hullámhosszán nagy a levegő abszorpciója, ezért a fényút teljes hosszán vákuumot kell biztosítani.
Csoportosítsa a gázlézereket műküdési hullámhossztartomány, átlagteljesítmény és üzemmód (cw, impulzus) alapján!
Mivel magyarázható a He-Ne és az alkáli-gőz lézerek közötti nagy hatásfok különbség?
Mi az oka annak, hogy a rézgőz lézer csak impulzus üzemmódban működtethető?
Mi a puffergázok szerepe a lézerek működésében?
Mi a jellemző hullámhossz-tartománya a semleges atom-, ion- és molekuláris lézereknek? Mi okozza az eltérést?
Miért könnyű a populációinverziót létrehozni excimer lézerek esetén?
[12.1] O. Svelto: Principles of lasers (4ed., Springer, 1998)
[12.2] K. Tradowski: A laser ABC-je (Műszaki könyvkiadó)
[12.3] B.V. Zhdanov, R.J. Knize, Review of alkali laser research and development, Optical Engineering 52(2), art. 021010 (2012)
[12.4] J.T. Verdeyen: Laser Electronics (3ed. Prentice hall, 1995)
[12.5] Open Access Encyclopedia for Photonics and Laser Technology (RP Photonics GmbH) http://www.rp-photonics.com/encyclopedia.html
Tartalom
A szabadelektron lézer (SZEL, angolul free-electron laser, FEL) olyan eszköz, amely alkalmas nagyintenzitású, koherens elektromágneses sugárzás előállítására a spektrumnak a mikrohullámoktól a röntgen tartományig terjedő tetszőleges részén. A nevében szereplő "szabadelektron" kifejezés arra utal, hogy, - ellentétben az eddig bemutatott lézerekkel -, a sugárzás létrehozása nem ionokhoz, atomokhoz, molekulákhoz vagy kristályrácshoz kötött elektronok energiaszintjei közötti átmenet során keletkezik, hanem - relativisztikus sebességgel mozgó - szabad elektron bocsátja ki azt. Emiatt a SZEL szigorú értelemben véve nem lézer, hiszen működése nem kényszerített emisszión alapul. Ugyanakkor az általa előállított sugárzás a lézerekre jellemző tulajdonságokkal rendelkezik, azaz a sugárzás nyalábszerűen, kis divergenciával terjed, kis sávszélességgel, ugyanakkor nagy teljesítménnyel és intenzitással rendelkezik és koherens.
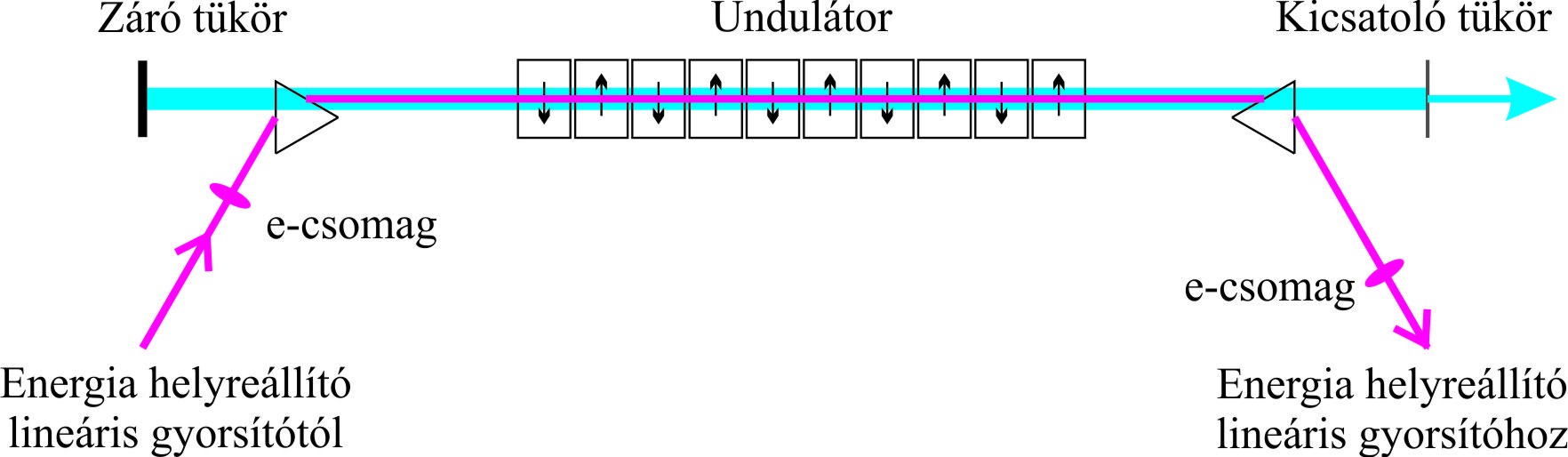
13.1. ábra. SZEL felépítése.
A SZEL általában sokkal nagyobb, mint más lézerek, de felépítésében (lásd 13.1 ábra) azokra hasonlít (1.8. ábra). A SZEL is tartalmaz egy rezonátorba helyezett erősítőt, és természetesen itt is szükség van energia bevitelre, azaz pumpálásra. A SZEL esetén az erősítés egy térben periodikus mágneses teret előállító eszközben, az undulátorban valósul meg. SZEL esetén a pumpálás a nagyenergiájú elektronok előállítását és/vagy az elektronok energiájának növelését jelenti, és az nem az erősítőben, hanem elkülönülten, mikrohullámú elektrongyorsítóban (általában szinkrotronban vagy linac-ban) történik. A SZEL-ek elsősorban ezek miatt az elektrongyorsítók miatt nagyméretűek. A SZEL-ek működéséhez relativisztikus sebességgel (azaz közel fénysebességgel) mozgó elektronokra van szükség. Ezeket az elektronokat a v sebességükön kívül más, a speciális relativitáselméletben használt mennyiségekkel jellemezhetjük. Ezek a c fénysebességhez viszonyított b = v/c relatív sebesség, a
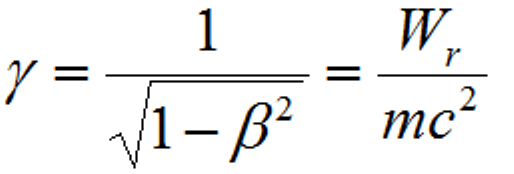 |
(13.1) |
relativisztikus faktor, vagy Lorentz-faktor, illetve az m nyugalmi tömegű, mc2 = 0,511 MeV nyugalmi energiájú elektron (MeV egységben mért) Wr (teljes) relativisztikus energiája. A következő alfejezetben megmutatjuk, hogy a SZEL által létrehozott sugárzás hullámhosszát a
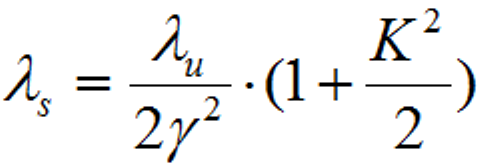 |
(13.2) |
egyenlet adja meg, ahol lu az undulátor mágneses terének a térbeli periódusa, és
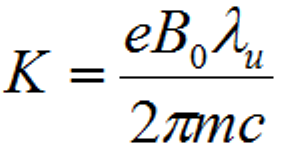 |
(13.3) |
az un. undulátor paraméter, amelynek (13.3) kifejezésében e az elektron töltését, B0 pedig az undulátorbeli mágneses térerősség csúcsértékét jelöli. A (13.2) egyenlet szerint a SZEL hullámhossza az elektronok energiájának négyzetével fordítottan arányos. Ez teszi lehetővé nagyon különböző hullámhosszon működő SZEL-ek építését. (13.2)-ben lu = 30 mm és K = 1 tipikus értékeket használva azt kapjuk, hogy 2 MeV elektronenergia esetén a SZEL a mikrohullámú tartományon fog működni, a lézer hullámhossza 1,5 mm lesz. 6 GeV-es elektronok esetén viszont röntgendiffrakciós vizsgálatokban alkalmazható, 1,6 Å hullámhosszú lézerimpulzusokat lehet előállítani.
2 MeV energiájú elektroncsomagok közvetlenül előállíthatóak egy elektronágyúval, ami egy termo- vagy fotókatódból és azt követő, azzal egybeépített mikrohullámú gyorsító üregből, valamint az azt meghajtó klisztronból áll. Az elektronágyú 1 - 2 méter hosszú. 6 GeV energiájú elektroncsomagok előállításához már nagyon összetett rendszerre van szükség, amely több gyorsító szakaszból áll, amelyek között elektroncsomag fókuszáló, manipuláló és diagnosztizáló eszközök helyezkednek el. A mikrohullámú elektrongyorsítókkal maximum 30 MeV/m gyorsítási gradienst lehet elérni. Ez alapján 6 GeV eléréséhez legalább 200 m tiszta gyorsítási hossz szükséges. A kiegészítő eszközök miatt az ilyen gyorsító hossza tipikusan több mint 500 m.
A SZEL-ek tehát nagy, bonyolult és ennek megfelelően igen költséges berendezések. Így világszerte mindössze néhány tucat működik belőlük. A nagy bekerülési és fenntartási költségük ellenére azért építenek ilyen berendezéseket, mert olyan kutatásokat lehet velük elvégezni, amelyeket semmilyen más eszközzel sem. A ma működő legmodernebb SZEL a Kaliforniában, Stanfordban 2010-re megépített LCLS röntgen szabadelektron lézer, aminek a honlapja: https://portal.slac.stanford.edu/sites/lcls_public/Pages/Default.aspx.
A fejezet végén az irodalomjegyzék további SZEL-ekkel kapcsolatos honlapokat tartalmaz.
Töltések mozgása elektromágneses sugárzást hozhat létre. Először tekintsünk egyetlen elektront! Ha egyenletes sebességgel mozog, akkor semmilyen sebesség esetén sem sugároz. Ha viszont az elektron gyorsul, és sebessége kicsi a fénysebességhez képest, akkor Larmor szerint
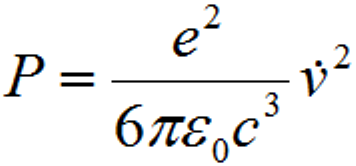 |
. | (13.4) |
teljesítménnyel sugároz, ahol ε0 a vákuum permittivitása. A (13.4) egyenletben a sebesség jele fölé helyezett pont az idő szerinti deriválást jelöli. (Ebben a fejezetben végig a fizikai mennyiség jele fölé helyezett ponttal jelöljük az időbeli deriválást.) A fénysebességet tetszőlegesen megközelítő elektronsebesség esetén a kisugárzott teljesítmény Liénard szerint
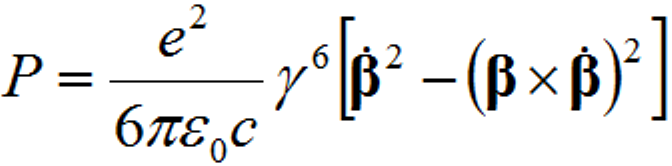 |
. | (13.5) |
Tekintsük a (13.5) egyenletet két fontos speciális esetben! Ha a gyorsulás a sebességgel párhuzamos, akkor a szögletes zárójelben a második tag eltűnik. Relativisztikus sebesség esetén a dinamika alapegyenlete
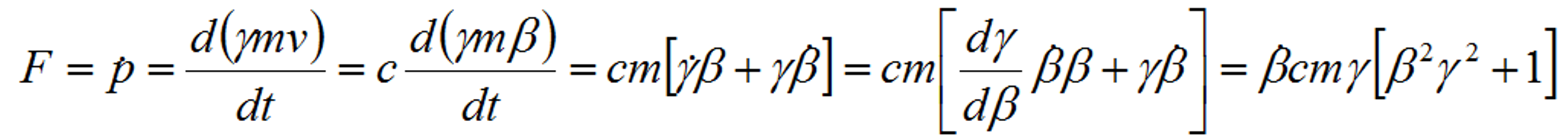 |
(13.6) |
alakú, ahol felhasználtuk a (13.1) kifejezést. (13.6) és (13.1) felhasználásával a
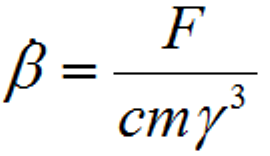 |
(13.7) |
kifejezéshez jutunk. Ezt a (13.5) egyenletnek a sebességgel párhuzamos gyorsulás esetére érvényes alakjába behelyettesítve a
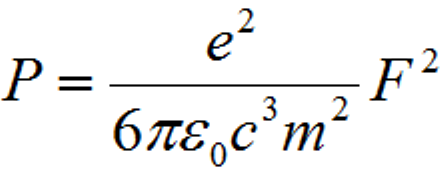 |
(13.8) |
kifejezést kapjuk.
Ha a gyorsulás a sebességre merőleges, akkor az erő munkája zérus, így az elektron energiája, és ezzel a g Lorentz faktor állandó. Emiatt (13.6) helyett az
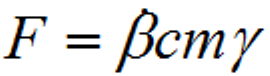 |
(13.9) |
egyszerű összefüggés érvényes. A (13.5) kifejezésben pedig a szögletes zárójel (β/γ)2-el egyenlő, és a kisugárzott teljesítményre a
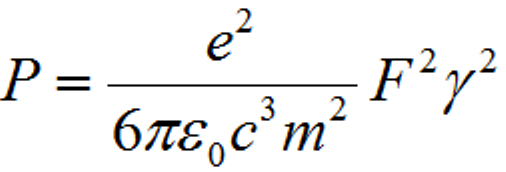 |
(13.10) |
végeredményt kapjuk.
(13.10) és (13.8) szerint ugyanakkora nagyságú külső erő g2-el intenzívebb sugárzást kelt akkor, ha a gyorsulás a sebességre merőleges, mint amikor a sebességgel párhuzamos. Ezt figyelembe kell venni az elektrongyorsítók tervezésénél is, hiszen a kisugárzott teljesítmény veszteséget jelent, csökkenti a gyorsítás hatékonyságát. (13.10) alapján megmutatható, hogy szinkrotronok esetén, ahol az elektronok r sugarú körpályán mozognak a sugárzás miatti energiaveszteség körüljárásonként
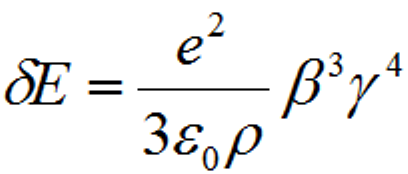 |
. | (13.11) |
Látható, hogy az energiaveszteség a körpálya sugarának növelésével csökkenthető. Azonban nagy g esetén a veszteség még r = 100 m esetén is jelentős. A (longitudinális gyorsítás miatt fellépő) sugárzás okozta energiaveszteség lineáris gyorsítók esetén általában elhanyagolható.
A (13.8) és (13.10) kifejezéseket összehasonlítva látható hogy sugárforrásként olyan gyorsítók használhatóak közvetlenül, amelyekben a gyorsított elektronok a sebességükre merőleges gyorsulással (is) rendelkeznek, azaz görbült pályán mozognak. Ilyen gyorsítók például a szinkrotronok. Ezekben az elektronok egyenes és íves szakaszok összességéből álló, közelítően kör alakú pályán haladnak. Az íves mozgást hajlító (bending) mágnesek (a legegyszerűbb esetben dipól-mágnesek) okozzák. Az elektronok ezeken az íves szakaszokon sugároznak. A kibocsátott sugárzás elegendően rövid r görbületi sugár, és elegendően nagy elektronenergia, illetve g faktor esetén nagyon intenzív lehet. A nagy elektronenergia nemcsak azért előnyös, mert az energia négyzetével arányos a sugárzás teljesítménye, hanem azért is, mert növekvő elektronenergiával a sugárzás egyre kisebb szögre korlátozódik, így könnyebben lehet azt használni. Az egyik legmodernebb szinkrotron sugárforrás a Chicago mellet található Argonne National Laboratory-ban működő Advanced Photon Source (APS, honlapja: http://www.anl.gov/). Ebben az elektronok energiája 7 GeV. Ezek a nagyenergiájú elektronok az APS esetén nem egyszerű dipól-mágnesek sarkai között elhaladva keltik a szinkrotron sugárzást, hanem undulátorok terében. Ez azzal az előnnyel (is) jár, hogy így az előállított sugárzás spektruma sokkal keskenyebb, mint dipól-mágnesek alkalmazása esetén lenne. A több tucat munkaállomáshoz tartozó undulátorok periódusa lu=1,8 cm-től 5,5 cm-ig terjed. Az előállított röntgen sugárzás hullámhossza a (13.2) egyenlet alapján (K=1-et feltételezve) ls=1÷3 Å. Az előállított sugárzást a világ különböző országaiból érkező kutatók tudják használni kísérleteikben. http://en.wikipedia.org/wiki/Synchrotron
A 13.2 ábra egy undulátort mutat sematikusan. A koordinátarendszer z tengelye alatt és fölött elhelyezkedő váltakozó irányú mágneses momentummal rendelkező permanens mágnesek a közéjük helyezett pólusvasak segítségével a z tengelyen egy y irányú, és a z koordinátával a
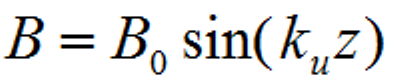 |
(13.12) |
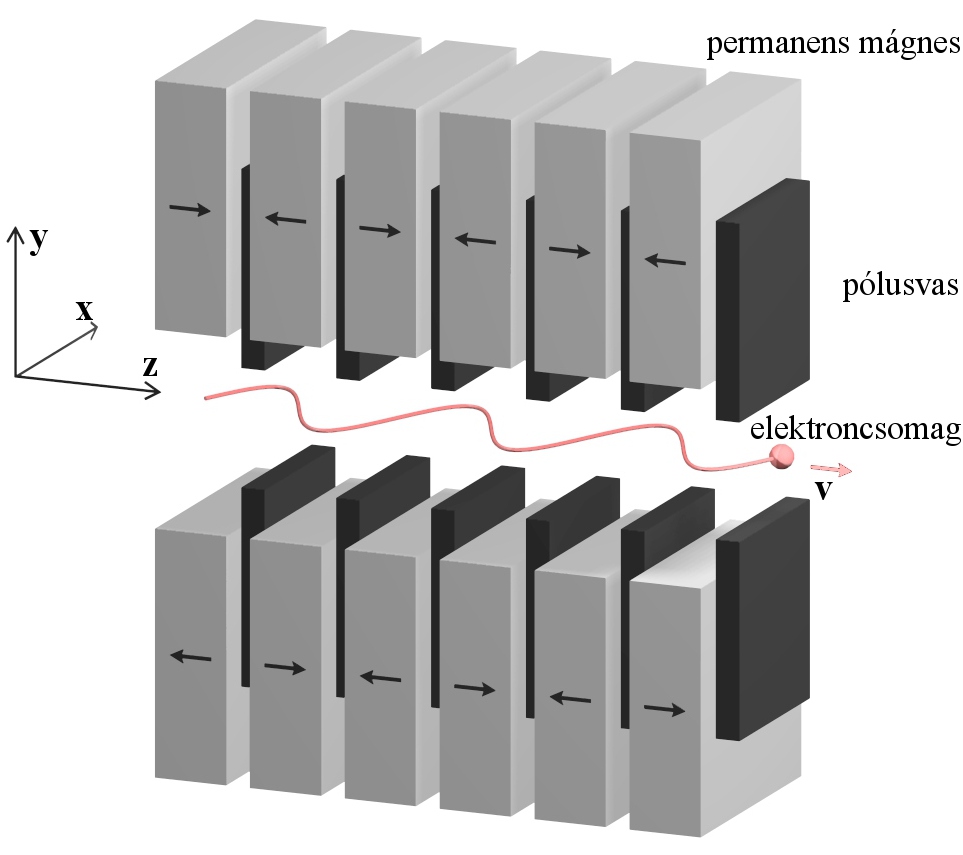
13.2. ábra. Undulátor felépítése.
kifejezésnek megfelelően változó nagyságú mágneses indukciót hoznak létre. (13.12)-ben ku=2p/lu és lu az undulátor mágneses terének a térbeli periódusa. Ha az undulátorba a z tengely közelében, azzal (közel) megegyező irányban egy elektron érkezik, akkor annak gyorsulását az
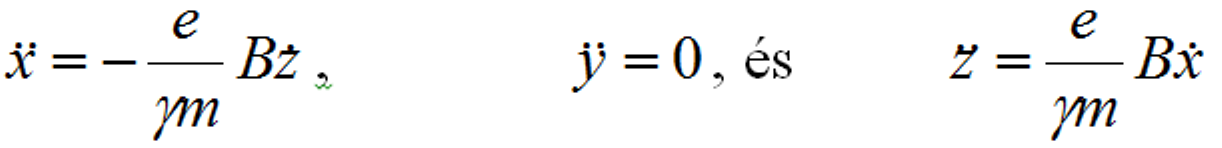 |
(13.13) |
egyenletek írják le, amelyeket a dinamika relativisztikus egyenletéből kapunk, ha kihasználjuk, hogy az elektronra ható Lorentz erő az elektron energiáját nem változtatja meg (g= állandó). A (13.13) egyenletrendszer elsőrendű közelítő megoldása
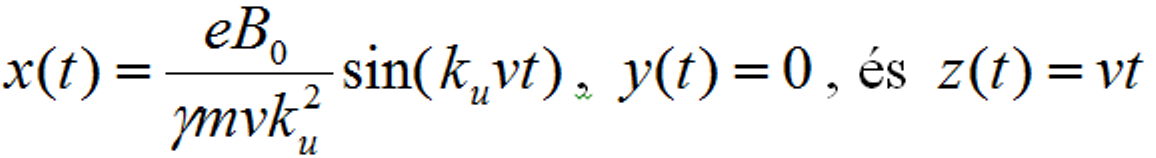 |
, | (13.14) |
amelyhez az dx/dt « dz/dt fennállása miatt alkalmazott dz/dt ≈ v = βc = állandó közelítés és az
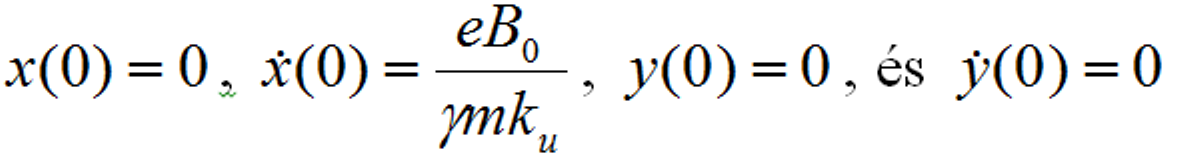 |
(13.15) |
kezdőfeltételek alkalmazásával jutunk. (13.14) alapján az elektron az undulátorban elsőrendű közelítésben az y = 0 síkban egy harmonikus pályán mozog:
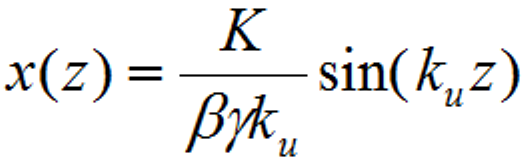 |
(13.16) |
szerint, ahol
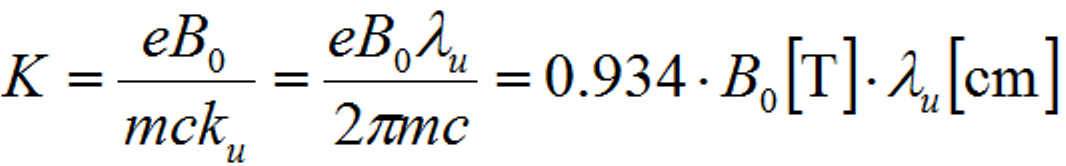 |
(13.17) |
a (13.3) szerinti undulátor paraméter. Ennek egy szemléletes jelentéséhez juthatunk a következők szerint. (13.16) alapján a keresztirányú sebesség
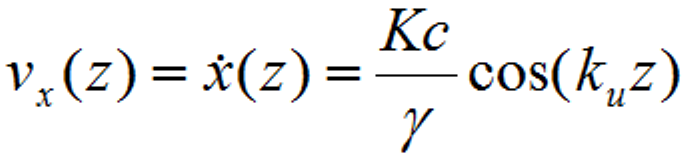 |
. | (13.18) |
Ebből, a longitudinális sebességet v = bc ≈ c-vel közelítve azt kapjuk, hogy az elektron sebességének az iránya maximum qmax ≈ K/g szöggel tér el az átlagos irányától.
Ha K nem sokkal kisebb, mint 1, akkor nem érvényes a (13.13) egyenletrendszer elsőrendű közelítése. Ekkor az elektron energiájának állandósága miatt az elektron sebességének z komponensére vz(z) ≠ v = állandó, hanem az a
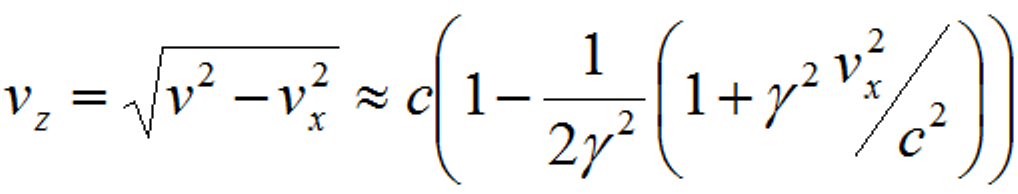 |
(13.19) |
egyenlettel meghatározott. (13.19)-be vx (13.18) alakját behelyettesítve kapjuk, hogy
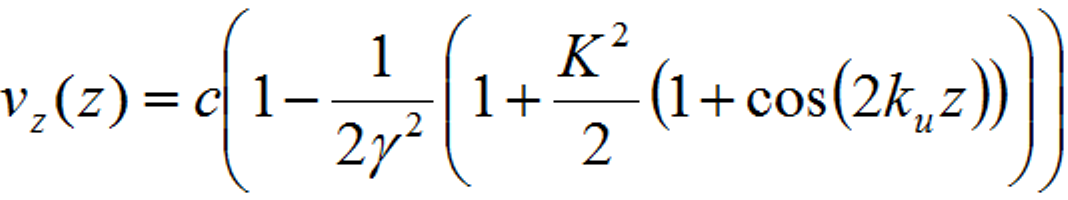 |
, | (13.20) |
aminek az átlagértéke
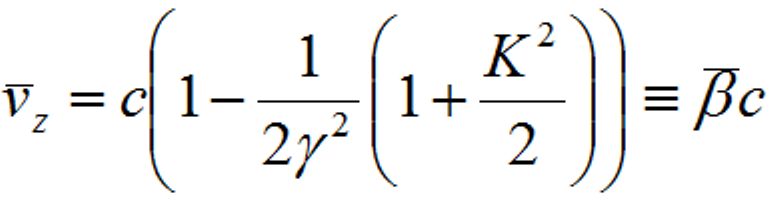 |
. | (13.21) |
Az elektron x és z koordinátájának az időfüggése másodrendű közelítésben:
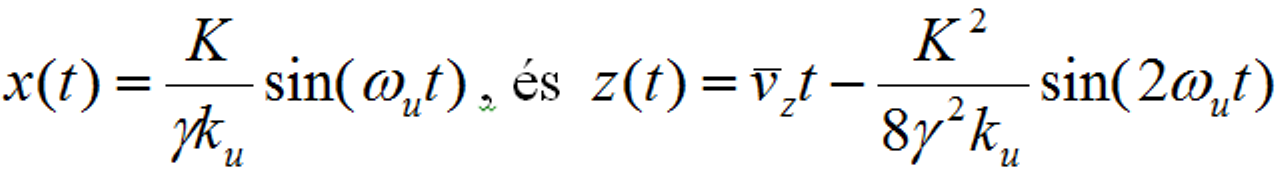 |
, | (13.22) |
ahol bevezettük az 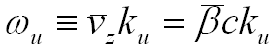 körfrekvenciát.
körfrekvenciát.
A (13.22) egyenletek alapján az elektron a 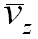 átlagsebességgel mozgó vonatkoztatási rendszerben egy 8-as alakú pályán mozog, transzverzálisan
ωu, longitudinálisan pedig 2ω
u
körfrekvenciával oszcillál. A transzverzális oszcilláció amplitúdója 8g/K-szor nagyobb, mint a longitudinálisé, a gyorsulások aránya pedig 2g/K. (13.5) alapján látható, hogy a kisugárzott teljesítmény a gyorsulás négyzetével arányos és az is könnyen megmutatható, hogy azonos nagyságú tranzverzális és longitudinális gyorsulások esetén g2-szer kisebb lenne a transzverzális gyorsulás miatt kisugárzott teljesítmény, mint a longitudinális gyorsulás miatti. Ezek alapján az undulátorban mozgó elektron által keltett sugárzás 4/K2-szer nagyobb részéért felelős a transzverzális gyorsulás, mit a longitudinális. Mivel K általában egy körüli érték, a kétféle gyorsulás által keltett sugárzás teljesítménye nagyságrendileg megegyezik. Azonban lényeges különbség van ezen sugárzások szög szerinti eloszlásaiban, amiket a
átlagsebességgel mozgó vonatkoztatási rendszerben egy 8-as alakú pályán mozog, transzverzálisan
ωu, longitudinálisan pedig 2ω
u
körfrekvenciával oszcillál. A transzverzális oszcilláció amplitúdója 8g/K-szor nagyobb, mint a longitudinálisé, a gyorsulások aránya pedig 2g/K. (13.5) alapján látható, hogy a kisugárzott teljesítmény a gyorsulás négyzetével arányos és az is könnyen megmutatható, hogy azonos nagyságú tranzverzális és longitudinális gyorsulások esetén g2-szer kisebb lenne a transzverzális gyorsulás miatt kisugárzott teljesítmény, mint a longitudinális gyorsulás miatti. Ezek alapján az undulátorban mozgó elektron által keltett sugárzás 4/K2-szer nagyobb részéért felelős a transzverzális gyorsulás, mit a longitudinális. Mivel K általában egy körüli érték, a kétféle gyorsulás által keltett sugárzás teljesítménye nagyságrendileg megegyezik. Azonban lényeges különbség van ezen sugárzások szög szerinti eloszlásaiban, amiket a
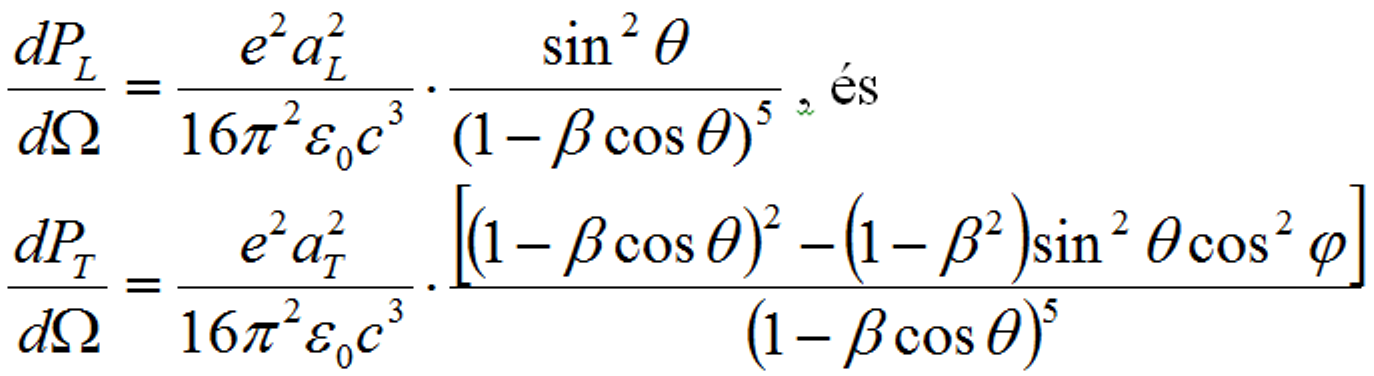 |
(13.23) |
kifejezések írnak le, ahol dΩ = sinθ dθ dφ a térszög-elem, θ az elektron átlagos haladási irányától (azaz az undulátor tengelyétől) mért szög, és φ a transzverzális gyorsulás irányától mért azimutális szög. A (13.23) eloszlásokat a 13.3 ábra mutatja K = 1 és g = 100 (b = 0.99995) esetén. Mint látható a transzverzális gyorsulás által keltett sugárzás az undulátor tengelye körüli (a maximális intenzitás felénél ≈ 0.8/g teljes nyílásszögű) térszögbe koncentrálódik. Ezzel szemben a longitudinális gyorsulás által keltett sugárzás az undulátor tengelye körüli ≈ 1/2g fél-nyílásszögű kúp irányában maximális, az elektron átlagos mozgásával pontosan megegyező irányban ilyen sugárzás nem keletkezik. Emiatt ez a sugárzás a SZEL működése során nem tud megerősödni, így ezzel a sugárzással a továbbiakban nem foglalkozunk.
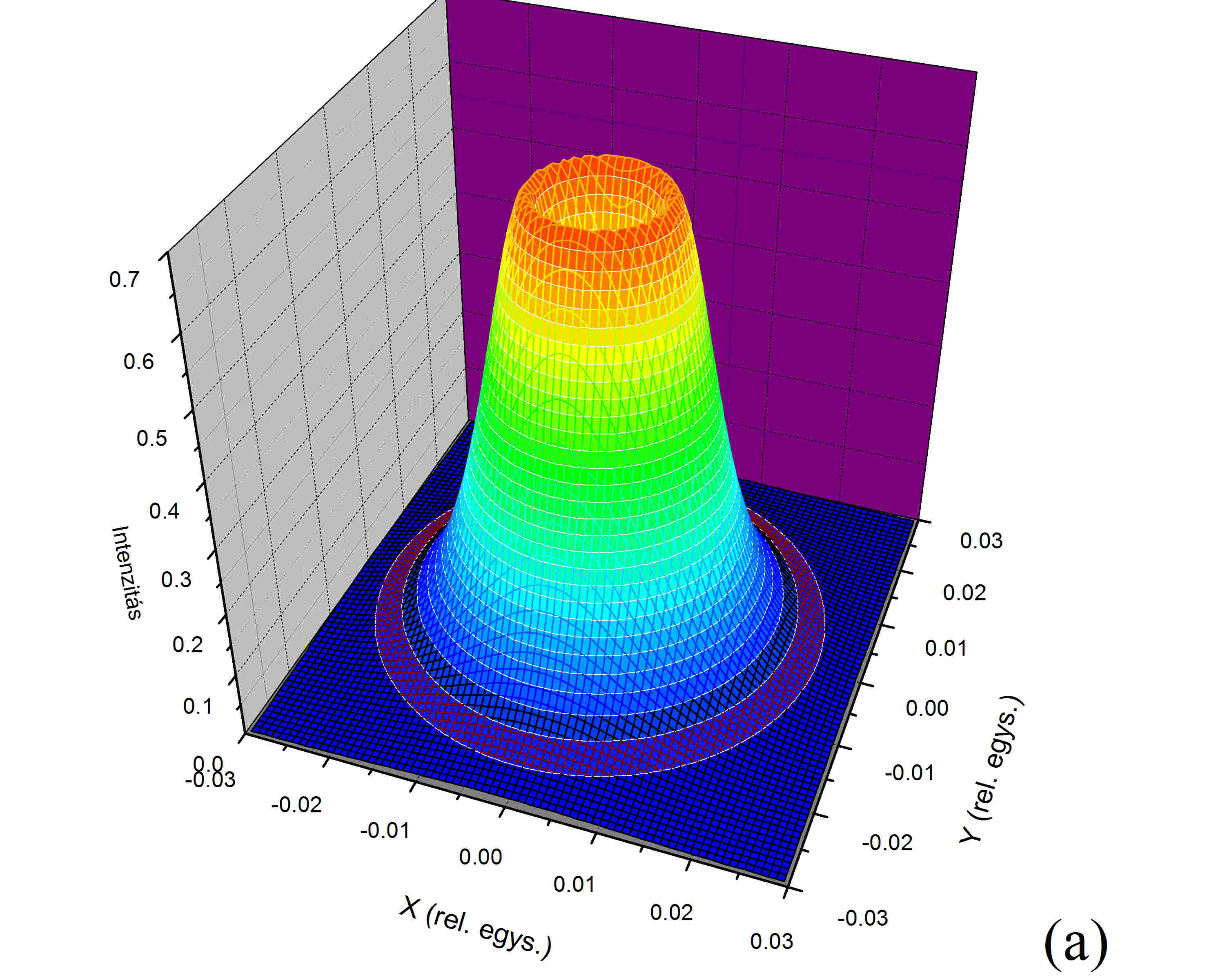 |
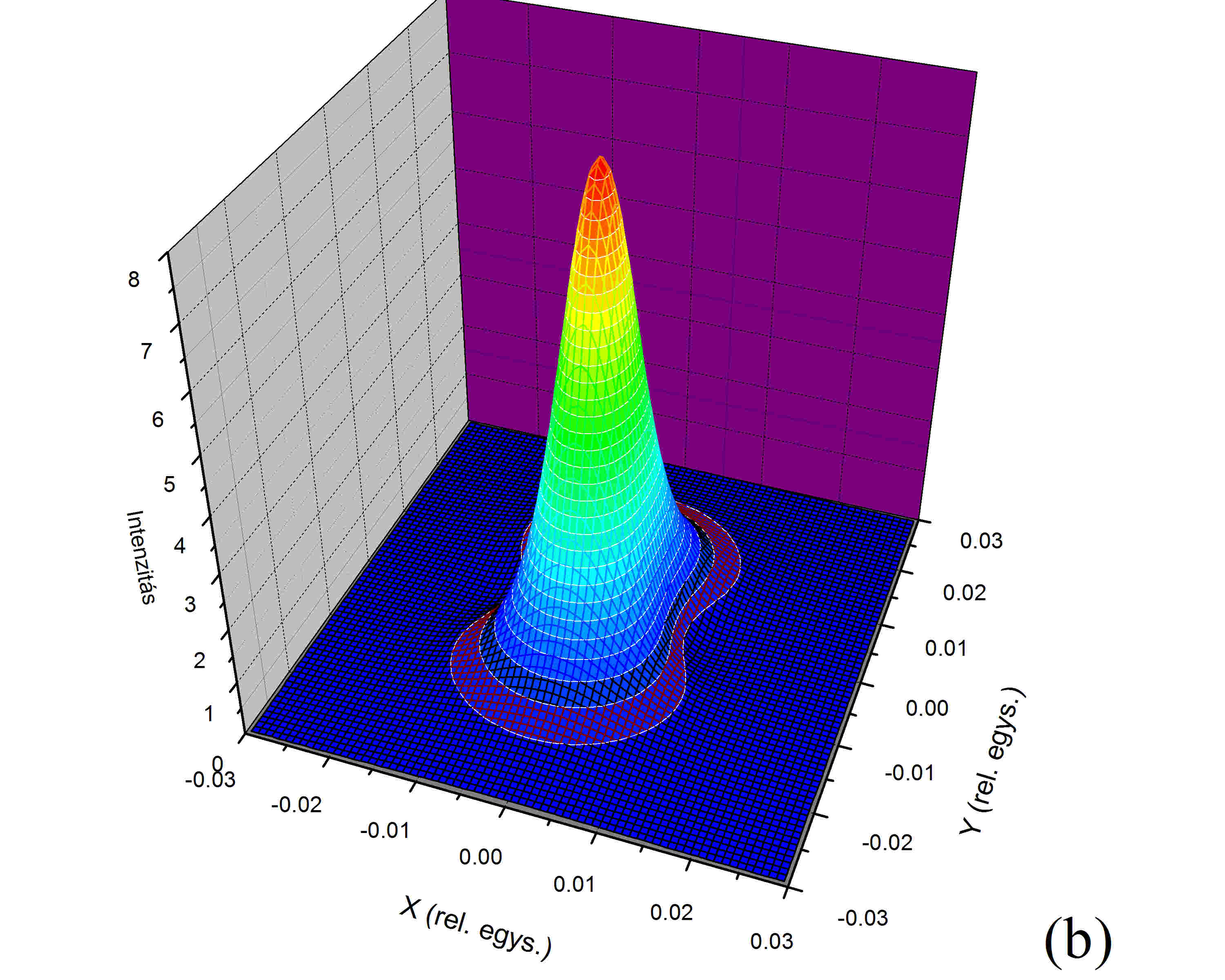 |
|
13.3. ábra. Longitudinális (a) és transzverzális (b) gyorsulás által keltett sugárzás szög szerinti eloszlása (13.23) alapján. | |
A 13.4 ábra alapján határozzuk meg az undulátorban keltett sugárzásnak az undulátortól távoli P pontban (BP » lu) észlelt hullámhosszát! Mivel az undulátorban a z tengely mentén vz átlagos sebességgel mozgó elektron lu térbeli periódussal oszcillál, az oszcillációjának frekvenciája
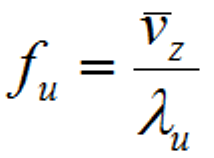 |
. | (13.24) |
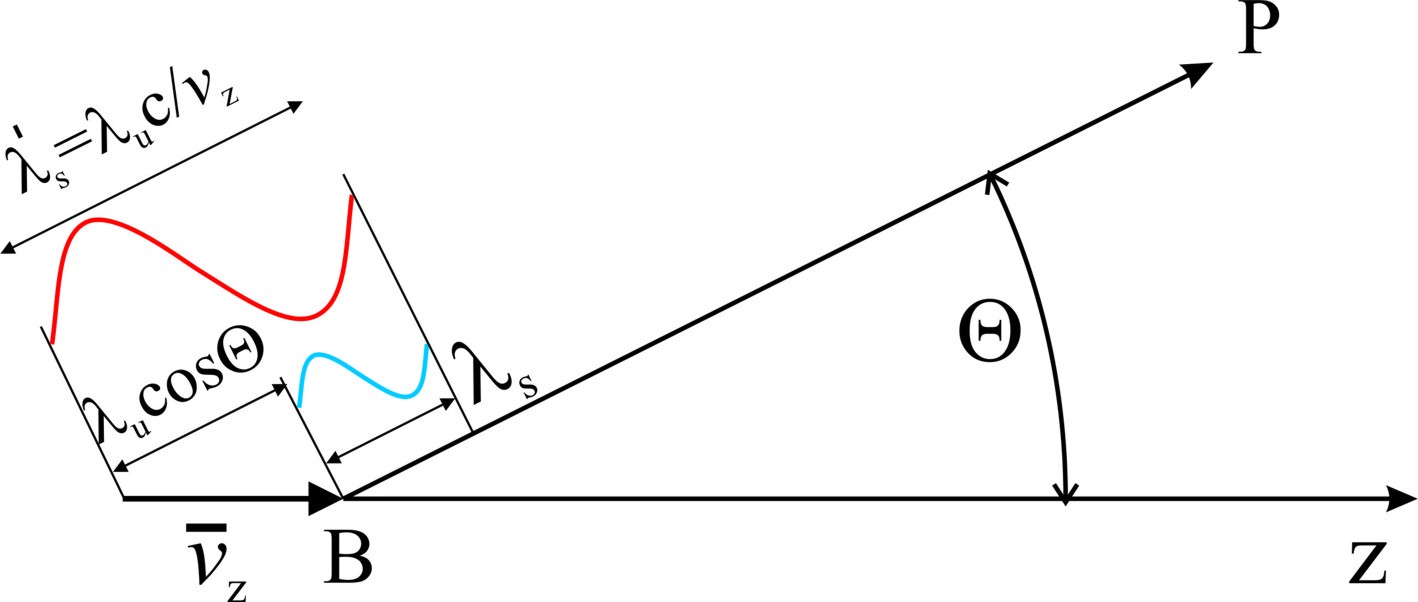
13.4. ábra. Sematikus rajz az undulátor sugárzás hullámhosszának a meghatározásához.
Az oszcilláló elektron ilyen frekvenciájú elektromágneses sugárzást kelt, amely
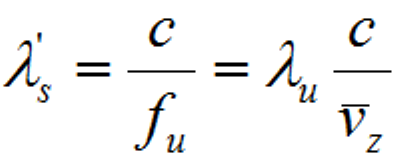 |
(13.25) |
hullámhosszú lenne álló elektron esetén. Mivel azonban az elektron 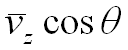 sebességgel közelít a P ponthoz, távolsága a P ponttól λ
u
cosθ értékkel csökken egy oszcilláció során, azaz a P irányában terjedő sugárzás hullámhossza
sebességgel közelít a P ponthoz, távolsága a P ponttól λ
u
cosθ értékkel csökken egy oszcilláció során, azaz a P irányában terjedő sugárzás hullámhossza
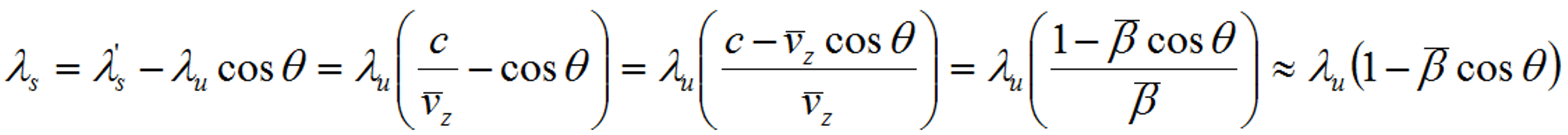 |
(13.26) |
értékre rövidül. Ebben a kifejezésben a koszinusz függvényt sorának első tagjával közelítve és az átlagsebesség (13.21) szerint alakját felhasználva kapjuk a végeredményt:
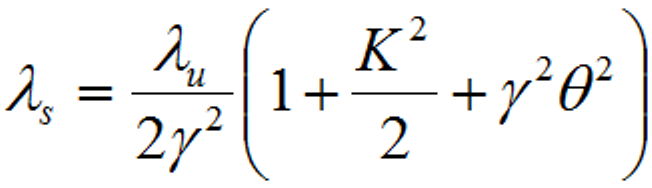 |
. | (13.27) |
A (13.5) kifejezés transzverzális esetre érvényes alakjába a gyorsulásnak a (13.22) első egyenletének idő szerinti kétszeres deriválásával kapott kifejezését behelyettesítve és idő szerint átlagolva azt kapjuk, hogy egy g kezdeti relativisztikus faktorral rendelkező elektron az undulátoron történő áthaladás során
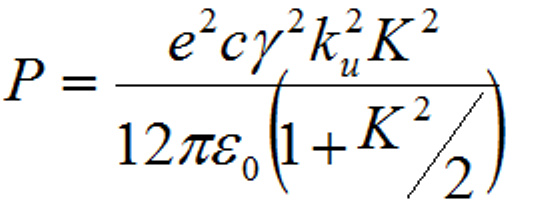 |
(13.28) |
teljesítménnyel sugároz a (13.27) szerinti frekvencián. (A teljes, -a longitudinális gyorsulástól származó sugárzást is figyelembevevő-, sugárzási teljesítmény a (13.28)-tól abban különbözik, hogy a nevezőben a zárójeles kifejezés nem lép fel.) (13.28) levezetésénél felhasználtuk azt, hogy az undulátorban mozgó elektron relativisztikus faktora (13.21) alapján
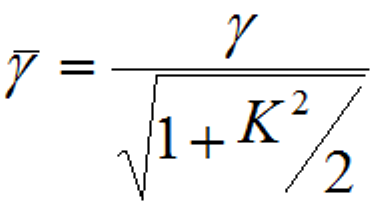 |
. | (13.29) |
K = 1, lu = 30 mm és g = 200 értékek esetén (13.28) alapján a kisugárzott teljesítmény P = 4,0∙10-11 W. Ebben az esetben egy Nu = 100 periódust tartalmazó undulátoron történő áthaladáskor egy elektron E = 4,0∙10-19 J energiát sugároz ki. Ennek a sugárzásnak a spektruma függ az undulátor Nu periódusainak a számától. Az I(ω) intenzitásspektrum az elektromos tér időbeli lefutása Fourier transzformáltjának a négyzetével arányos. Emiatt
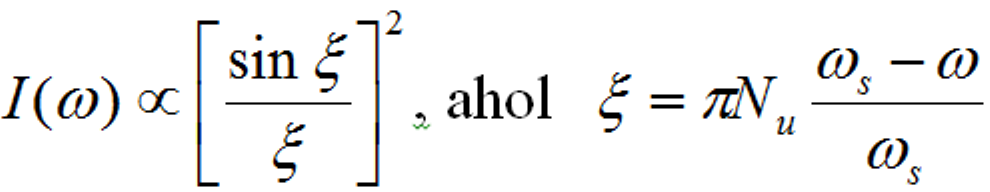 |
, | (13.30) |
ωs pedig a (13.27) szerinti hullámhossznak megfelelő körfrekvencia. E szerint az egy elektron által kibocsátott udulátorsugárzás sávszélessége az undulátor periódusainak számával fordítottan arányos.
A SZEL-ek mikrohullámú elektrongyorsítói általában néhány ps időtartamú és nC maximális nagyságrendű össztöltéssel rendelkező elektroncsomagokat gyorsítanak. Mivel ezekben az elektroncsomagokban az elektronok rendezetlenül helyezkednek el, a teljes csomag által kibocsátott sugárzás energiáját az elektroncsomag egyes elektronjai által keltett sugárzások energiáinak az összegezésével kapjuk. Ez alapján egy 1 nC töltésű elektroncsomag a fenti példa paraméterei esetén E = 2,5∙10-9 J = 2,5 nJ energiájú inkoherens elektromágneses impulzust sugároz. Ennél hat nagyságrenddel nagyobb energiájú impulzusok előállítására is képesek a modern SZEL-ek. Ez úgy lehetséges, hogy koherensen sugároznak, szemben az általunk eddig vizsgált inkoherens (spontán) sugárzással. Nézzük meg, hogy hogyan lehet koherens sugárzást előállítani SZEL-el!
Az undulátorban relativisztikus sebességgel mozgó elektron a mozgási energiájának rovására tud sugározni. Spontán sugárzás esetén az undulátoron történő egy áthaladáskor kisugárzott energia a (13.29) és (13.30) egyenletek közötti paragrafus szerint sok nagyságrenddel kisebb, mint az elektron teljes energiája. Az undulátor mágneses tere önmagában nem tudja megváltoztatni az elektron energiáját, hiszen csak az elektron sebességére merőleges erőt tud okozni. Azonban, ha a SZEL-ben kialakul a lézerműködés és emiatt az undulátor mágneses terén kívül egy
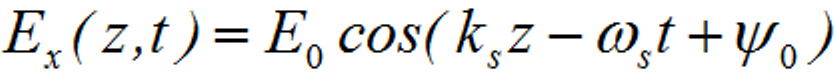 |
(13.31) |
egyenlettel leírható x irányú elektromos térerősséggel rendelkező erős elektromágneses sugárzási tér van jelen az undulátorban, akkor az elektron Wr energiája a
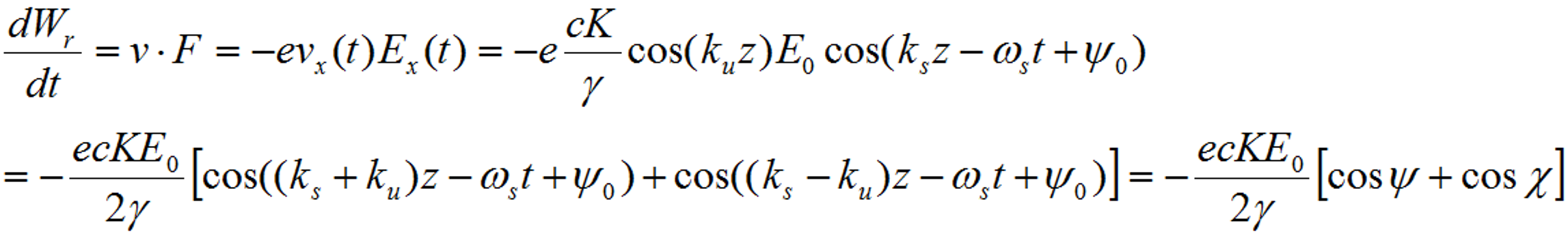 |
(13.32) |
egyenlet szerinti sebességgel változik az idővel. Megmutatható, hogy ha az elektron sebessége (illetve g faktora), a sugárzás ls hullámhossza és az undulátor lu periódusa olyan viszonyban állnak, hogy teljesül a (13.2) szerinti rezonancia feltétel, akkor az elektron undulátorban történő mozgása során Ψ = konstans. Ilyen esetben, mivel
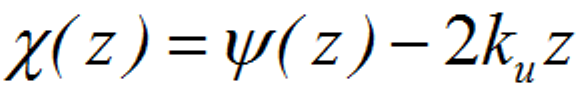 |
, | (13.33) |
χ(z) gyorsan változik és már egy undulátor periódus alatt kiátlagolódik. Emiatt a (13.32) egyenlet jobboldalán a szögletes zárójelben lévő második tag elhagyható. Az elektroncsomaggal együtt mozgó rendszerben a terjedési irány mentén a ζ koordinátájú helyen elhelyezkedő elektronhoz a
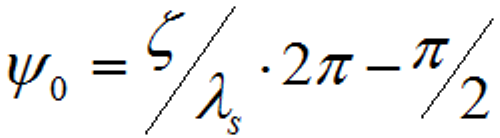 |
. | (13.34) |
összefüggés szerint Ψ0 kezdőfázis tartozik. A (13.32) és (13.34) egyenletek szerint az elektroncsomagban a különböző ζ helyen elhelyezkedő elektronra időben állandó, de ζ-től függő sebességű energiaváltozás lesz jellemző. Egymástól ls/2 távolságra lesznek olyan helyek ahol az energiaváltozás sebessége ellentétes, de maximális (ecKE0/2g) abszolút értékű. A ζ függő energiaváltozás ζ szerinti sebesség-modulációt okoz. Ez a sebesség-moduláció pedig elektron-sűrűség modulációt eredményez mivel a gyorsabb elektronok bizonyos repülési út alatt utolérik a lassabbakat. Ezt a folyamatot, amit mikrocsomósodásnak nevezünk, mutatja sematikusan a 13.5 ábra.
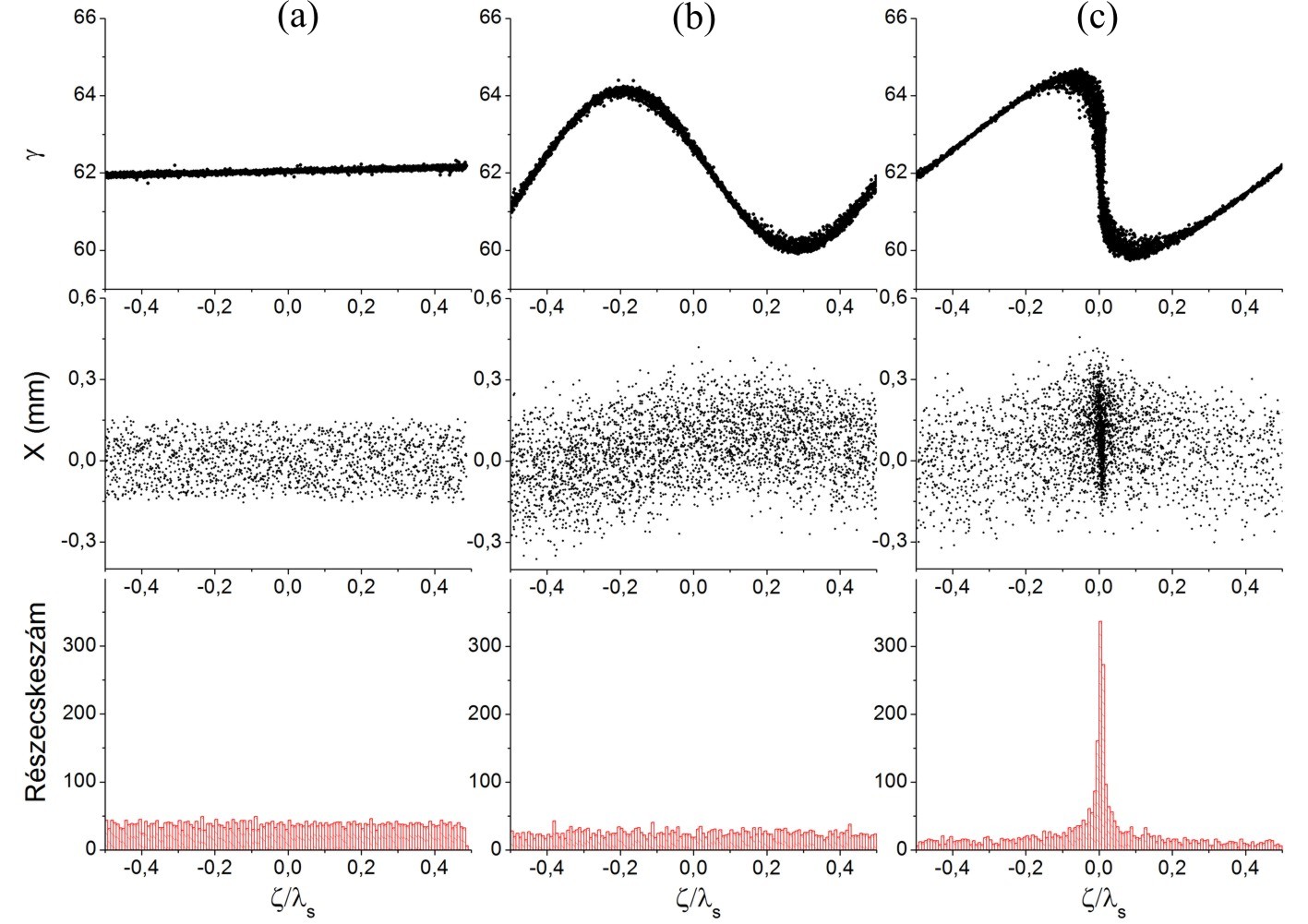
13.5 ábra. A mikrocsomósodás folyamata. Az ábrasorozat a csomósodás előtt (a), a csomósodás közben (b), és a csomósodás befejezésekor (c) mutatja az elektroncsomag ls hosszú részét. A felső sorban az elektronok energia eloszlása, a középsőben az elektronok térbeli elhelyezkedése látható a z-x koordináta mentén, ahol z az elektronok haladási iránya. Az alsó sor az elektronok töltéssűrűségének z-függését mutatja.
A mikrocsomósodás eredményeként létrejövő elektronsűrűség maximumok közelében elhelyezkedő elektronok által kisugárzott tér közel azonos fázisú. Az így elért konstruktív interferencia eredményeként több nagyságrenddel nagyobb energiájú sugárzás jön létre, mint az inkoherens (spontán) sugárzás esetén.
Az undulátorban jelenlévő, a rezonancia-feltételnek megfelelő frekvenciájú elektromágneses sugárzás tehát mikrocsomósodást okoz. Azonban kezdetben nincs jelen intenzív sugárzás, csak a zajos, véletlenszerű idő- és spektrális eloszlású spontán undulátor sugárzás. Ennek és a kezdetben véletlenszerű elektronsűrűség eloszlással rendelkező elektroncsomagnak a kölcsönhatásából folyamatosan alakul ki a keskenysávú lézersugárzás és a mikrocsomósodott elektroncsomag. A koherens lézerműködés a hagyományos lézerekben is a spontán emisszióból alakul ki. Ott azonban a kényszerített emisszió során keletkező foton fázisa rögzített a kényszerítőhöz, a SZEL-ben viszont a mikrocsomosódásnak végbe kell mennie ahhoz, hogy a fény erősítése fázis-rögzítetten történjen. Ez a folyamat a (távoli, közepes, vagy közeli) infravörös vagy a látható tartományon működő SZEL-ek esetén, amelyek rezonátort tartalmaznak, és amelyekben az erősítés kicsi (az undulátoron történő áthaladás során <100 %) a lézerfénynek a rezonátorban történő sokszori körbefutása során alakul ki. Ezekkel a továbbiakban nem foglalkozunk, csak annyit jegyzünk még meg, hogy ezekben a SZEL erősítési függvény, azaz a SZEL impulzusának az undulátoron történő áthaladása során létrejövő relatív energia növekménye a ξ relatív frekvencia függvényében
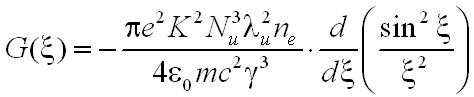 |
(13.35) |
alakú, ahol ne az (átlagos) elektronsűrűség. Ezt a kifejezést (13.30)-al összehasonlítva látható, hogy G(ξ) a spontán undulátorsugárzás (normalizált) frekvencia szerinti deriváltjával arányos. G(ξ)-t a 13.6 ábra mutatja.
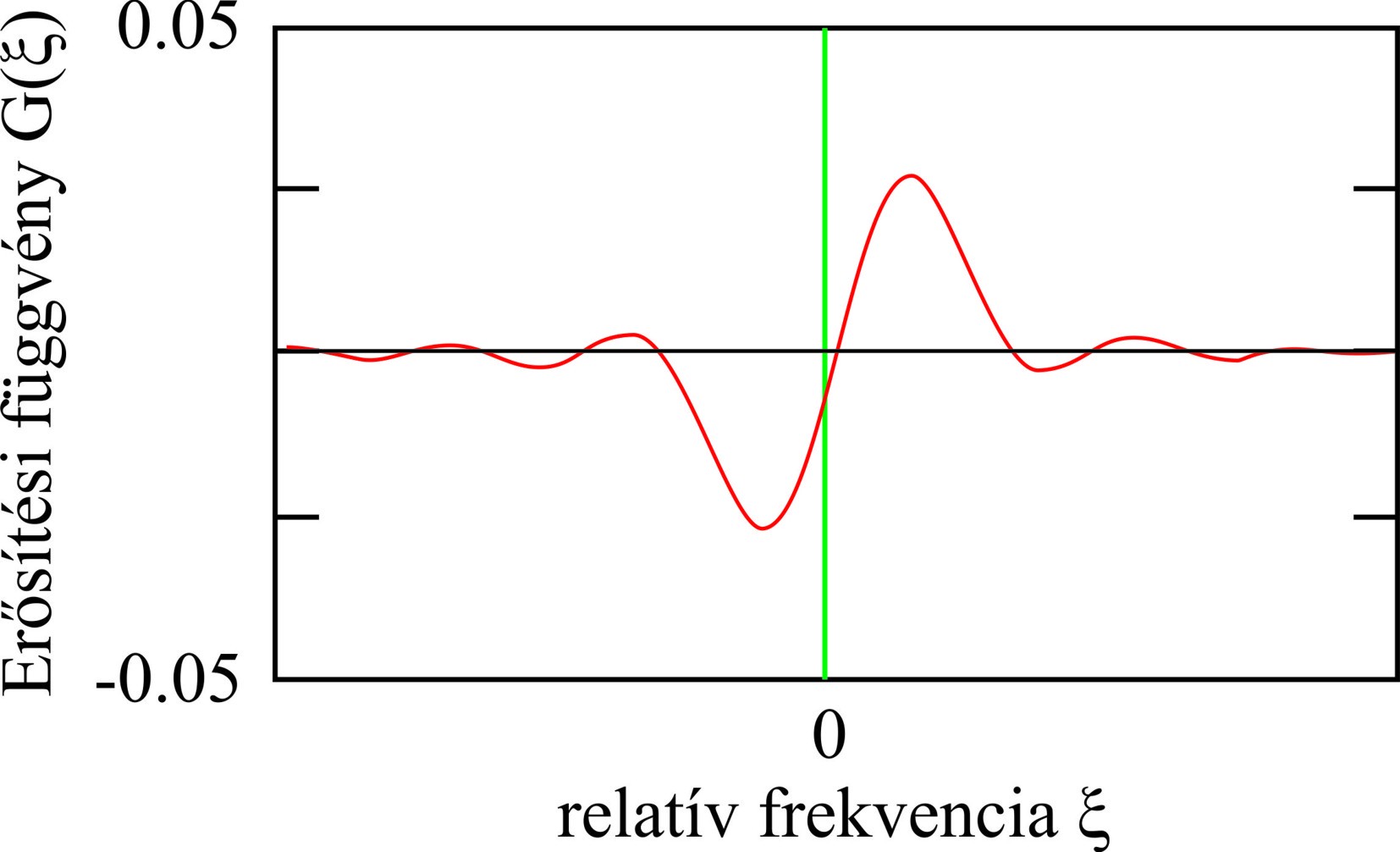
13.6. ábra. Kis erősítésű SZEL tipikus erősítési függvénye.
Napjainkban azok a SZEL-ek tekinthetők a legfontosabbaknak, amelyek az extrém UV vagy, még inkább, amelyek a röntgen tartományban működnek, hiszen ezeknek nincs igazán alternatívája a hagyományos lézerek között. A röntgen tartományon nem lehet nagy reflexiójú tükröket készíteni, emiatt a röntgen SZEL-ek nem tartalmaznak rezonátort. Az UV és röntgen SZEL-ek működése általában az ön-erősített spontán emisszió (ÖESE, angolul: self-amplified spontaneous emission, SESA) folyamatán alapul. Azaz a mikrocsomosódás és a spontán emisszióból történő intenzív lézerfény fentebb leírt kölcsönös kialakulásának olyan módján, amikor ez a folyamat az elektroncsomagnak az undulátoron történő egyszeri áthaladása során kialakul. A 13.7 ábra sematikusan mutatja, hogy ÖESE SZEL esetén hogyan függ a SZEL undulátorban kialakuló lézer impulzus energiája az undulátor hosszától. Az energia növekedése a görbe nagy részén exponenciálisan növekszik az undulátor hosszával, azaz leírható a
 |
(13.36) |
függvénnyel, ahol Le-t erősítési hossznak nevezzük. Erre a részre az jellemző, hogy már jelen van bizonyos mértékű mikrocsomósodás, és annak mértéke növekszik az undulátorban történő terjedéssel. Ezt a részt egy telítődési szakasz követi, ahol a mikrocsomósodás már csaknem teljes mértékű, további fejlődésre nincs lehetőség. Ezen a szakaszon a lézer energia növekedése teljesen befejeződik, esetleg némi csökkenése is bekövetkezik. Az undulátor elején, amikor még nincs jelen mikrocsomósodás, lényegében csak a spontán undulátor sugárzással nő a "lézerimpulzus" energiája. Ilyenkor a "lézerimpulzus" teljes mértékben zajszerű. A telítési szakaszban a lézerimpulzus térbeli koherenciája teljes, spektruma viszonylag keskeny, időbeli koherenciája rossz, az idő-sávszélesség szorzata tipikusan 3-10 szerese a transzformáció határoltnak. Az UV és lágy-röntgen tartományon működő ÖESE SZEL-ek esetén beoltás (angolul: seeding) segítségével lehet jó időbeli koherenciával rendelkező SZEL impulzusokat előállítani. Ez a technika abból áll, hogy az undulátorba az elektroncsomaggal egyidejűleg beküldenek olyan lézerimpulzust aminek a frekvenciája a rezonancia frekvencia, vagy annak páratlan tört része. Ilyen impulzust ultrarövid impulzusok magasharmonikus keltésével (angolul: high harmonic generation, HHG) lehet előállítani. A beoltás - ahogy azt a 13.7 ábra is mutatja -, azzal az előnnyel is jár hogy a telítődés rövidebb undulátor hossznál következik be.
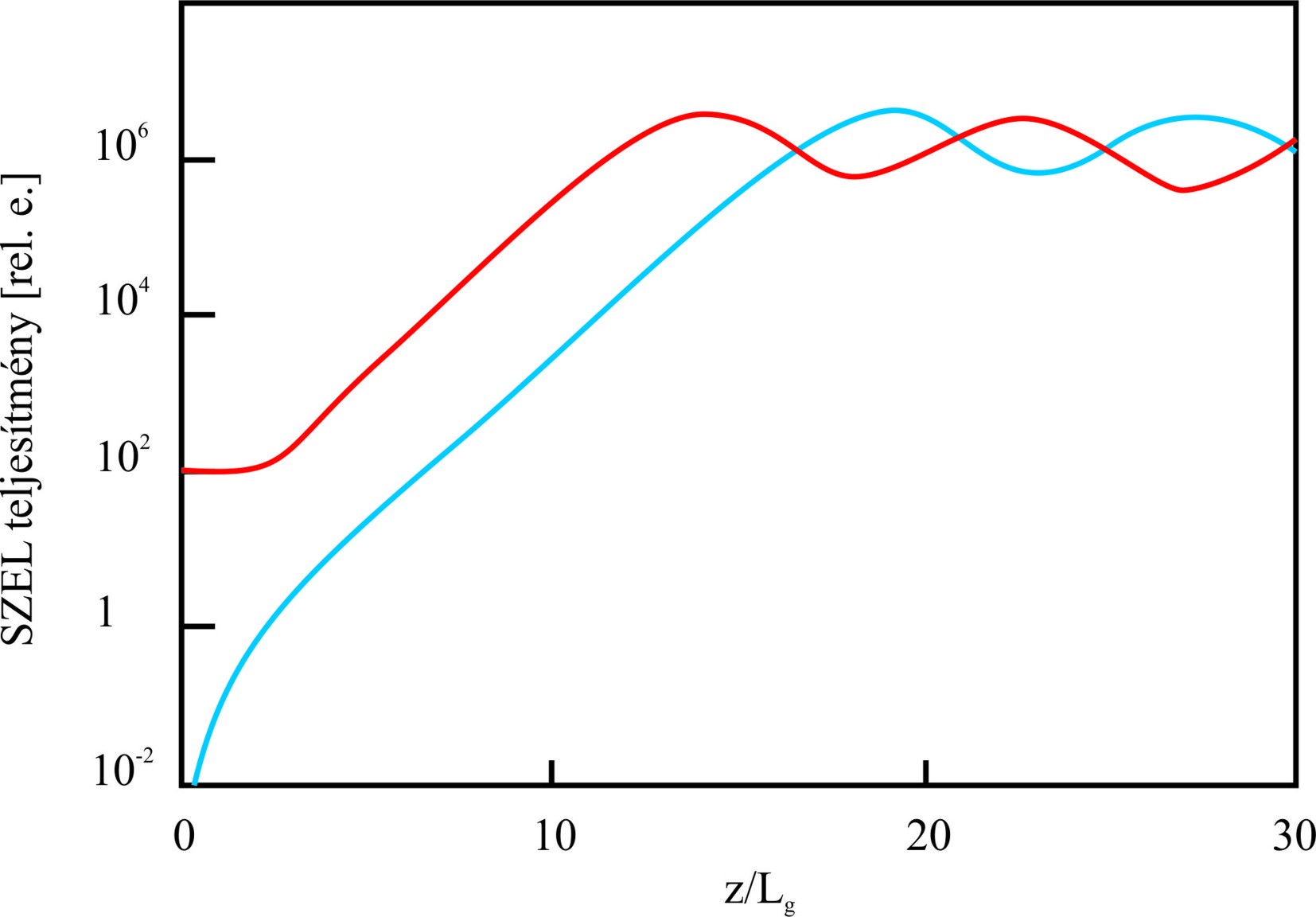
13.7. ábra. ÖESE SZEL lézerimpulzus energiájának az undulátorhosszal történő változását sematikusan bemutató görbe (kék görbe). A piros görbe beoltott SZEL esetét mutatja.
A SZEL-ek elméletének részletes bemutatására ebben a rövid áttekintésben nincs lehetőség. Megadunk viszont néhány, a nagy erősítésű SZEL-ek (pl. ÖESE SZEL) működésének leírásában fontos szerepet játszó mennyiségre vonatkozó kifejezést. Az erősítés- és a tértöltés paraméter
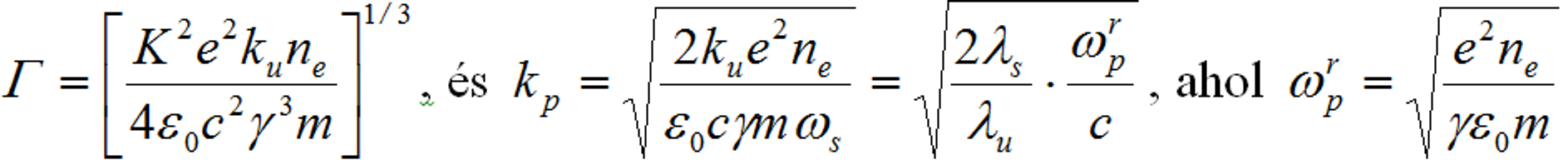 |
(13.37) |
a relativisztikus plazma (kör)frekvencia. A tértöltés miatt fellépő erők akkor hanyagolhatóak el, ha G>>kp. Az erősítési hossz
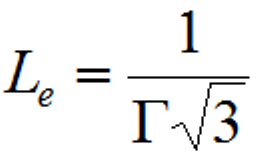 |
(13.38) |
A SZEL paraméter, vagy Pierce paraméter
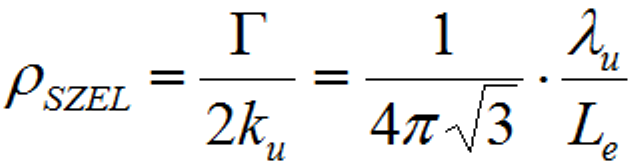 |
. | (13.39) |
A SZEL sugárzásának telítési teljesítménye megadható a
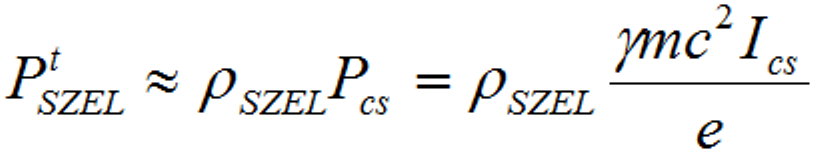 |
(13.40) |
összefüggés szerint, ahol Ics az elektroncsomag által keltett áram. Az ÖESE SZEL sugárzásának sávszélessége
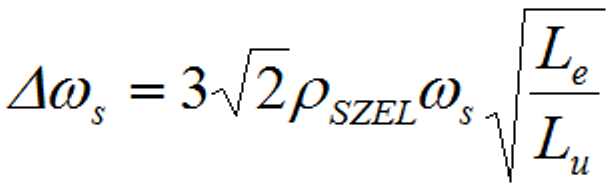 |
, | (13.41) |
ahol Lu = lu Nu az undulátor hossza.
Veszteség ciklotronban egy elektron esetén, elektroncsomag esetén.
A (13.5) egyenletből kiindulva mutassa meg, hogyan függ a sebességgel párhuzamos, illetve arra merőleges gyorsulás esetén a kisugárzott energia a gyorsulástól!
A (13.28) kifejezésből kiindulva számolja ki, hogy egy elektron az undulátor egy periódusán áthaladva átlagosan hány fotont bocsát ki!
Az elektron energiaváltozási sebességét megadó (13.32) (első) egyenlet egy undulátor periódusra történő alkalmazásával mutassa meg, hogy csak páratlan rendű felharmonikusra alakulhat ki erősítés SZEL-ben a Θ = 0 irányban.
A (13.35) egyenlet, illetve a 13.6 ábra alapján a kis erősítéssel rendelkező SZEL erősítési spektrumának a rezonanciafrekvenciánál kisebb frekvencián van a maximuma. Adjon magyarázatot erre!
[13.1] Peter Schmüser, Martin Dohlus, Jörg Rossbach: Ultraviolet and Soft X-ray Free-Electron Lasers (Springer, (Berlin Heidelberg 2008). DOI: 10.1007/978-3-540-79572-8, ISBN: 978-3-540-79571-1, e-ISBN: 978-3-540-79572-8, ISSN: 0081-3869, e-ISSN: 1615-0430)
[13.2] David J. Griffiths: Introduction to electrodynamics (Prentice Hall 1999, ISBN: 0-13-805326-X)
[13.3] John David Jackson: Klasszikus elektrodinamika (Typotex Budapest 2004, ISBN: 963-9548-06-5)
Web oldal a legfontosabb szabadelektron lézerekről:
http://sbfel3.ucsb.edu/www/vl_fel.html
Modern szabadelektron lézerek web oldalai:
http://www.psi.ch/swissfel/swissfel/
https://portal.slac.stanford.edu/sites/lcls_public/Pages/Default.aspx
Tartalom
Az elmúlt 20 év gyors technikai fejlődésének köszönhetően [14.1-2] napjainkban olyan lézerimpulzusok állnak a kísérletezők rendelkezésére, melyek csak néhány optikai ciklus hosszúságúak. Ez a látható, illetve a közeli infravörös tartományban 10 fs körüli impulzus időbeli hosszaknak felel meg. Emlékeztetőül a femto prefixum 10-15 szorzót jelent, így 1 fs = 10-15 s időnek felel meg. Ilyen rövid impulzusok viselkedése már jelentősen eltérhet a jól ismert monokromatikus hullámok esetében megszokottól. Ebben a fejezetekben röviden áttekintjük, hogy milyen jelenségek lépnek fel az ultrarövid fényimpulzusok terjedése során, és ezek hogyan tárgyalhatók. A következő fejezetben pedig azt foglaljuk tömören össze, hogy ezen fényimpulzusok tulajdonságai, és az itt leírt jelenségek kísérletileg hogyan vizsgálhatók meg.
Rövid fényimpulzusok terjedésének leírásánál szokásos eljárás a hely- és időfüggő térmennyiségek Fourier-féle felbontását használni, mert így a közeg linearitását kihasználva, az impulzus terjedésének vizsgálata visszavezethető az impulzust alkotó monokromatikus komponensek terjedésének a vizsgálatára. A tárgyalásnál az egyszerűség miatt csak lineárisan poláros fénnyel foglalkozunk, és a koordinátarendszert úgy választjuk meg, hogy a térerősség az y tengely irányába mutasson. Ekkor az E = E(r, t) térerősséget célszerű az
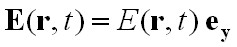 |
(14.1) |
alakba felírni, ahol ey az y tengely irányába mutató egységvektor (a polarizáció irányát megadó vektor). A Fourier-transzformációs párok segítségével a térerősség monokromatikus hullámok szuperpozíciójaként állítható elő, azaz
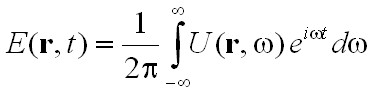 |
, | (14.2) |
ahol
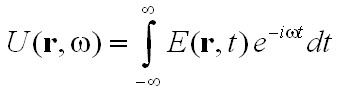 |
. | (14.3) |
Homogén és izotróp közeget feltételezve, E = E(r, t) az (1.1) hullámegyenletet, míg U(r, ω) az (1.4) Helmholtz-féle egyenletet elégítik ki. Az U(r, ω) komplex mennyiséget célszerű az
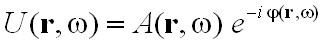 |
. | (14.4) |
exponenciális alakban felírni, ahol az A(r, ω) amplitúdó nem-negatív valós, míg a φ(r, ω) fázis valós mennyiség. Az U(r, ω) eiω t (az ω körfrekvenciájú) monokromatikus összetevő fázisfelületeit, vagyis a térben azon felületeket, ahol a hullám fázisa állandó, az
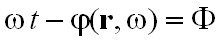 |
(14.5) |
egyenlet határozza meg, ahol Φ egy állandó (a fázis értéke az adott felületen). Ahogy az idő változik, úgy az állandó fázisú felületek a térben mozognak. Ha t0 és t1 időpontok között a fázisfront elmozdul, a fázisfront terjedési idejét, azaz τ p = t1 - t0 mennyiséget fáziskésésnek nevezzük, és a (14.5) egyenlet alapján, nyílván a
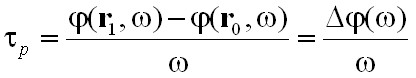 |
(14.6) |
formulából számítható ki, ahol r0 és r1 a két fázisfelület egy pontjába mutató helyvektorok és Δφ = φ(r1, ω) - φ(r0, ω). Egyszerűen megmutatható, hogy a fázisfelületek sebessége, az u.n, fázissebesség a
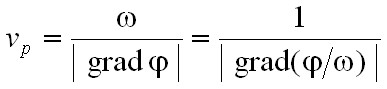 |
(14.7) |
formulával számítható ki [14.3]. Egy szokásos homogén síkhullám összetevő esetén φ(r, ω) = kr, ahol k a hullámszám vektor. Ekkor visszakapjuk a fázissebességre a jól ismert
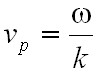 |
(14.8) |
képletet. Ha a síkhullám egy n abszolút törésmutatójú közegben terjed, akkor k = 2π/(λ/n) és ω = 2πν, valamint a c = λν összefüggéseket felhasználva
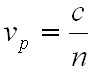 |
(14.9) |
képletet kapjuk, ahol ν a frekvencia, c és λ a vákuumbeli fénysebesség illetve hullámhossz.
Tegyük fel, hogy az impulzus sávszélességének megfelelő frekvenciatartományban a fázis a frekvenciának lineáris függvényeként közelíthető, azaz
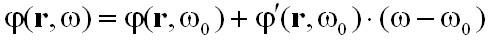 |
, | (14.10) |
ahol ω0 az u.n. központi körfrekvencia (vagy más néven vivő körfrekvencia) és a deriválást a körfrekvencia szerint végezzük. A (14.10) közelítést, továbbá a (14.4) és a (14.2) egyenletek használva az
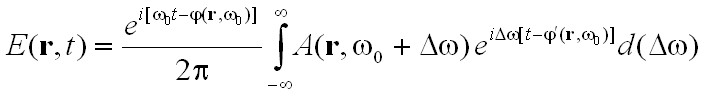 |
(14.11) |
összefüggést kapjuk, ahol az integrálásnál áttértünk a Δω = ω - ω0 változóra. Az impulzus terjedésének szempontjából érdekes kérdés, hogy egy tetszőleges, de rögzített r pontban mikor maximális az I(r, t) = | E(r, t) |2 formulával adott intenzitás. Egy adott t időpontban ezen r pontok halmaza a térben egy felületet definiál, melyet impulzusfrontnak szokás nevezni. Mivel az A amplitúdó nem negatív, a (14.11) egyenlet alapján belátható [14.4], hogy az intenzitás a
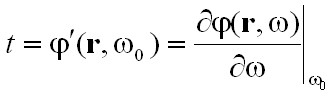 |
(14.12) |
időpontban maximális. Ahogy az idő változik, úgy - a fázisfronthoz hasonlóan - az impulzusfront is mozog a térben. A fáziskéséshez hasonlóan szintén értelmezhető a (14.12) egyenlet alapján a csoportkésésnek nevezett, és a
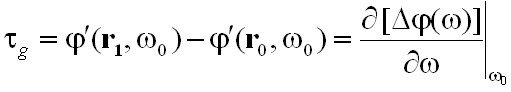 |
(14.13) |
képlettel definiált mennyiség, ahol r0 és r1 most a t0, illetve a t1 időpontbeli impulzusfrontok egy pontjába mutató helyvektorok. A fázissebességhez hasonlóan megmutatható [14.4], hogy az impulzusfront a
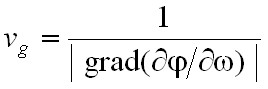 |
(14.14) |
u.n. csoportsebességgel terjed. A már említett - ω = ω(k) diszperziós relációjú - homogén síkhullám esetén, a φ(r, ω(k)) = kr fázist behelyettesítve a (14.14) általános képletbe, a
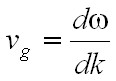 |
(14.15) |
eredményt kapjuk. Továbbá egy n abszolút törésmutatójú közegben terjedő síkhullám esetén egyszerű számolással a
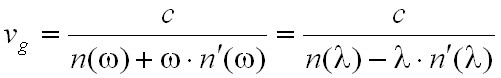 |
(14.16) |
formula adódik, ahol a vessző a függvény argumentum szerinti deriváltat jelöli. A nevezőben lévő mennyiséget ng = n - λ dn/dλ, a törésmutatóval analóg módon, szokás csoport-törésmutatónak (vagy csoportindexnek) nevezni, hiszen belőle a csoportsebesség a fázissebességhez hasonlóan számítható ki (lásd a (14.9) formulát).
Tekintsünk egy diszperzív közegben a z tengely irányába terjedő, a z = 0 síkban (az intenzitást tekintve) τ0 időbeli hosszúságú és ω0 központi körfrekvenciájú síkhullám fényimpulzust, azaz a térerősség időfüggése a z = 0 síkban legyen
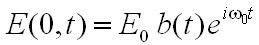 |
, | (14.17) |
ahol a b(t) a térerősség burkolója és E0 a maximális amplitúdó. Az impulzus z irányban terjedő monokromatikus síkhullámok szuperpozíciójaként állítható elő, azaz
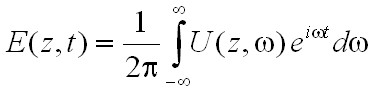 |
. | (14.18) |
Amennyiben a közeg a monokromatikus komponenseket nem csillapítja, csak a fázist befolyásolja a terjedés, akkor
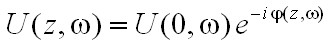 |
, | (14.19) |
ahol φ(z, ω) a diszperzív közeg által létre hozott fázistolás, és U(0, ω) az E(0, t) Fourier-transzformáltja, vagyis
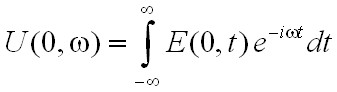 |
. | (14.20) |
A (14.17) explicit függést és a Fourier-transzformációra vonatkozó eltolási tételt használva,
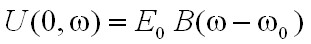 |
, | (14.21) |
ahol B(ω) a b(t) burkoló Fourier-transzformáltja. Amennyiben a diszperzív közeg egy n = n(ω) törésmutatóval leírható közeg, úgy a terjedés során a fázistolás
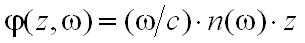 |
(14.22) |
A (14.18) egyenletet használva már kiszámolhatjuk a diszperzív közegben terjedő impulzus elektromos térerősségét. Az elméleti modellezés során gyakran időben Gauss-görbével leírható burkolóval szokás számolni, mert a valódi impulzusok időbeli lefutását jól közelíti, ráadásul a fázistolásra a központi frekvencia körül parabolikus közelítést használva, a (14.18) egyenlet analitikusan kiszámítható. Gaussos időbeli burkoló esetén
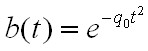 |
, | (14.23) |
amelynek a Fourier-transzformáltja
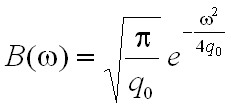 |
. | (14.24) |
Ha az impulzus időbeli hossza τ0, akkor
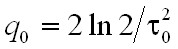 |
. | (14.25) |
Érdemes megjegyezni, hogy a Gauss-görbe Fourier-transzformációs párjára vonatkozó formulák nem csak valós, hanem komplex q0 paraméter esetén is érvényesek, amit hamarosan ki is használunk majd. Közelítsük a fázist másodrendig az ω0 központi körfrekvencia körüli Taylor-sorával, azaz legyen
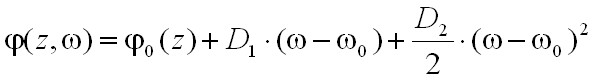 |
, | (14.26) |
ahol φ0 egy frekvencia független fázis, D1 a csoportkésés és D2 az u.n. csoportkésés-diszperzió:
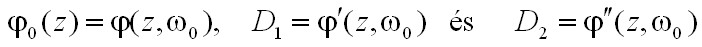 |
, | (14.27) |
ahol a vesző a körfrekvencia szerinti deriválást jelöli. Ezeket a formulákat a (14.18) egyenletbe helyettesítve, Gauss-os időbeli burkoló esetén és a fázistolásra parabolikus közelítés használva, a térerősség az
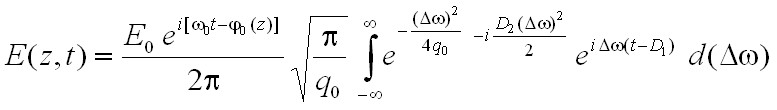 |
(14.28) |
formulával számítható ki, ahol az integrálnál végrehajtottuk a Δω = ω - ω0 helyettesítést. Ha bevezetjük a
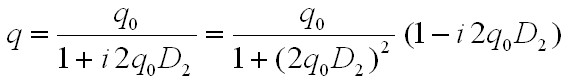 |
(14.29) |
mennyiséget, akkor a (14.28) egyenletbeli inverz Fourier-transzformáció kiszámolása visszavezethető a (14.24) függvény inverzére, mivel a q változóval
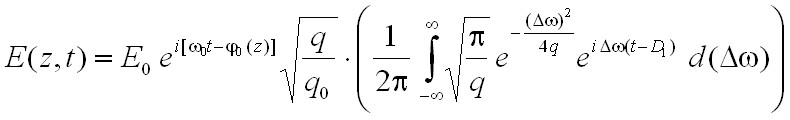 |
. | (14.30) |
Mivel a zárójelben lévő tényező pontosan a (14.24) függvény inverz Fourier-transzformáltja a (t - D1) időpontban, azaz a (14.23) egyenletbeli b(t) függvény a (t - D1) helyen, így
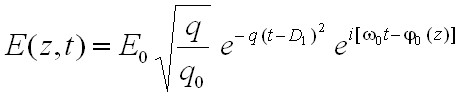 |
. | (14.31) |
A (14.29) egyenletet felhasználva,
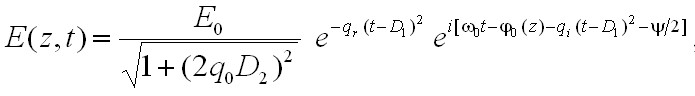 |
, | (14.32) |
ahol qr és qi a q paraméter valós illetve képzetes része, azaz q = qr + iqi, valamint
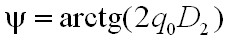 |
. | (14.33) |
A (14.32) egyenletből több fontos jelenség megállapítható. Egyrészt látszik, hogy a burkoló a D1 csoportkésésnek megfelelő idővel késik, továbbá a D2 csoportsebesség-diszperziótól függően csökken az amplitúdó és növekszik a burkoló szélessége, vagyis az impulzus időben D2-től függően kiszélesedik. Az impulzus τ időbeli hosszát a (14.25) egyenlet felhasználásával számolhatjuk ki, csak q0 és τ0 helyett qr-rel és τ mennyiségekkel kell számolnunk:
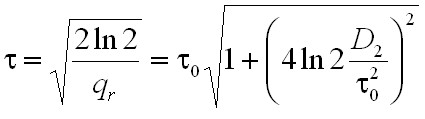 |
. | (14.34) |
A D2 csoportsebesség-diszperzió definíciójából és a fázis (14.22) egyenletbeli alakjából látszik, hogy D2 arányos a z koordinátával, így a z irányú terjedés során egyre nagyobb lesz. Nagy z értékek esetén a τ-t megadó (14.34) egyenletben a nagy négyzetszám mellett az 1 elhanyagolható, így az impulzus hossza jó közelítéssel a z koordinátával arányosan növekszik. Hasonló okok miatt, nagy z értékekre az impulzus amplitúdója 1/z-vel arányosan csökken. A (14.32) egyenletből még az is látható, hogy az impulzus
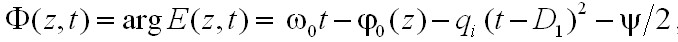 |
, | (14.35) |
fázisában megjelenik egy időben parabolikus tag is, aminek megfelelően az
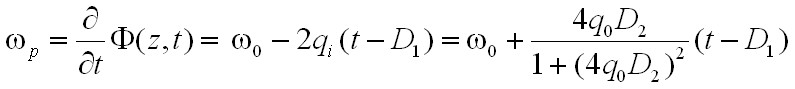 |
. | (14.36) |
u.n. pillanatnyi körfrekvencia az időtől függ. Ezt a jelenséget csörp-nek szokás nevezni, amely az angol chirp szónak a magyar kiejtéssel írt alakja.
A teljesség kedvéért megjegyezzük, hogy a közeg fázistolására harmadrendű Taylor-féle polinom közelítést használva, a térerősség az
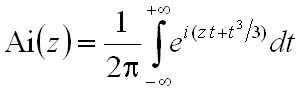 |
(14.37) |
formulával a komplex síkon értelmezett Airy-féle függvénnyel fejezhető ki:
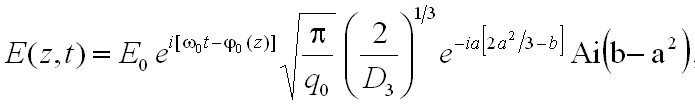 |
, | (14.38) |
ahol D3 az u.n. harmadrendű diszperzió, a fázistolás frekvencia szerinti harmadik deriváltja a központi frekvencián, azaz
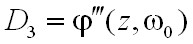 |
, | (14.39) |
továbbá
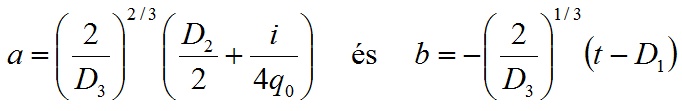 |
. | (14.40) |
Érdemes megjegyezni, hogy a (14.22) egyenletbeli fázistolás esetén a harmadrendű esetig a fázisderiváltak a következő formulákkal számíthatók ki:
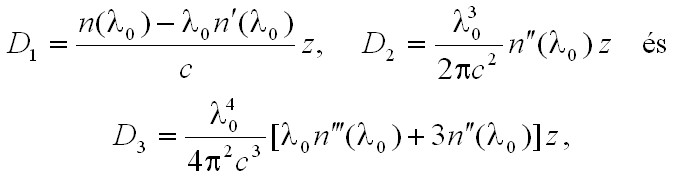 |
. | (14.41) |
ahol λ0 = 2πc/ω0 a (vákuumbeli) központi hullámhossz, és a törésmutató és a deriváltjainak diszperzióját a gyakorlatban sokkal használt (vákuumbeli) hullámhosszal fejeztük ki.
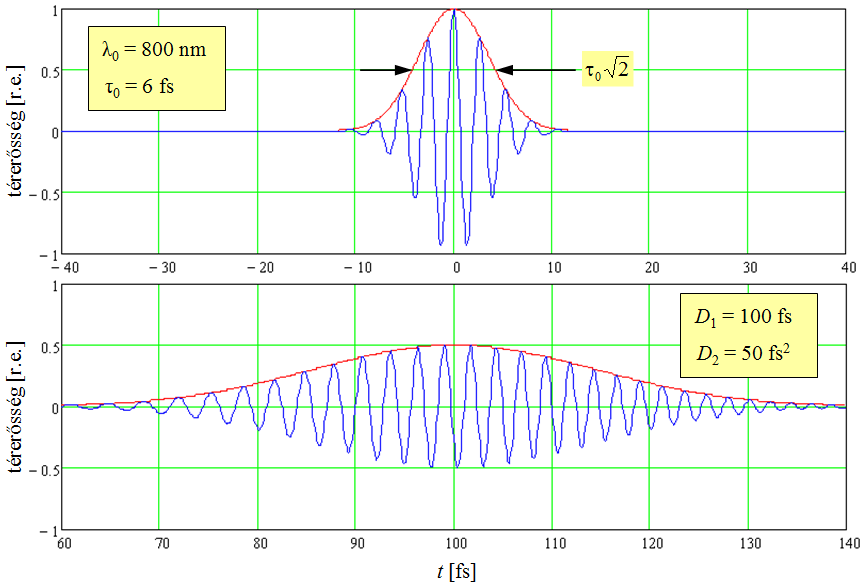
14.1. ábra. Felül: Kezdetben τ0 = 6 fs hosszúságú, λ0 = 800 nm központi hullámhosszú Gauss-görbe időbeli burkolójú impulzus térerősségének (kék görbe) és burkolójának (piros görbe) időbeli lefutása. Alul: A térerősség és burkolójának időfüggése D1 = 100 fs csoportkésésű és D2 = 50 fs2 csoportsebesség-diszperziójú parabolikus fázistolással leírható terjedés esetén.
A 14.1. ábrán megfigyelhetjük a diszperziónak a térerősség időbeli lefutására gyakorolt hatását. A számolást D1 = 100 fs csoportkéséssel és D2 = 50 fs2 csoportsebesség-diszperzióval végeztük el. A kezdeti impulzus intenzitásra vonatkozó hossza τ0 = 6 fs, míg a központi hullámhossz λ0 = 800 nm. Láthatjuk, hogy a piros színnel ábrázolt burkoló maximuma valóban a csoportkésésnek megfelelő 100 fs-nál van. A maximális amplitúdó az eredetinek a felére csökkent, továbbá az impulzus jelentősen kiszélesedett. Jól megfigyelhető térerősség frekvenciájának a időbeli változása, azaz a csörp is. A rezgések frekvenciája idővel növekszik, vagyis az alacsony frekvenciájú komponensek nagyobb sebességgel, míg a nagyobb frekvenciájú komponensek kisebb sebességgel terjednek. Ezt megfigyelhetjük a térbeli terjedést mutató animáción is.
Az ultrarövid fényimpulzusok optikájában fontos szerepet játszanak azok az optikai elemek, melyek egy monokromatikus hullám terjedési irányát a hullámhosszuktól függően változtatják meg. Ilyen például az optikai prizma és rács. Ezeknek a segítségével az impulzust alkotó monokromatikus komponensek fázisa változtatható, és így az impulzus időbeli hosszát manipulálhatjuk [14.1-2]. Rácsokból és prizmákból készíthetők u.n. impulzuskompresszorok vagy nyújtók [14.1-2]. Például a kompresszorok segítségével az előző fejezetben tárgyalt diszperzív közegbeli terjedés okozta kiszélesedést kompenzálhatjuk bizonyos mértékig, míg a nyújtókkal megnövelhetjük az impulzushosszat, és így csökkenthetjük az intenzitást, mellyel például a nagy intenzitások által okozott nemlineáris hatások és anyagroncsolás elkerülhető. Később a kinyújtott impulzus ismét kompresszorral ismét összenyomható. A továbbiakban azt vizsgáljuk meg, hogy az impulzusfrontra milyen hatással van a szögdiszperzió.
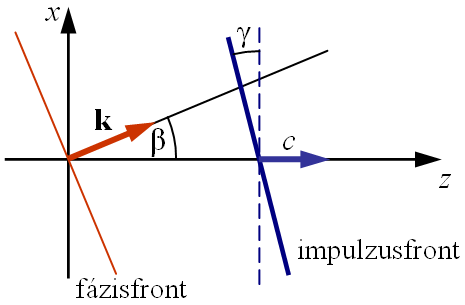
14.2. ábra. A szögdiszperzió hatásának számolásánál használt jelölések értelmezése.
Tekintsünk most is kezdetben a (14.17) egyenlettel leírható időfüggésű rövid fényimpulzust, és tegyük fel, hogy az impulzust alkotó monokromatikus síkhullám komponensek terjedési iránya függ az ω körfrekvenciától. A leggyakoribb esetben a terjedési irányok (a hullámszám-vektorok) egy síkba esnek, ezt itt most a diszperzió síkjának fogjuk nevezni. A számolás egyszerűsítése céljából a vonatkoztatási rendszert válasszuk meg úgy, hogy a diszperzió síkja legyen az (z, x) sík, és az ω0 központi körfrekvenciához tartozó terjedési irány legyen a z-tengely (14.2. ábra). Jelölje β az ω körfrekvenciájú komponens terjedési irányának a z-tengellyel bezárt szögét, ahogy az a 14.2. ábrán látható. A szögdiszperzió miatt a β szög függ a körfrekvenciától, azaz β = β(ω), és a koordinátarendszer speciális választása miatt β0 = β(ω0) = 0.
Az ω körfrekvenciájú komponens körhullámszám-vektorát a
 |
(14.42) |
összefüggés adja meg, amit felhasználva, a síkhullám összetevő fázisa
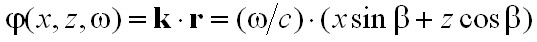 |
. | (14.43) |
A térerősség a monokromatikus komponensek szuperpozíciója, azaz
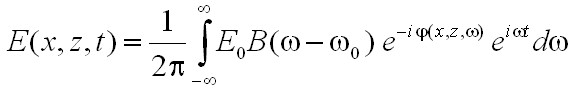 |
, | (14.44) |
ahol most is B(ω) a b(t) burkoló Fourier-transzformáltja. A t időpontbeli impulzusfrontot a (14.12) egyenlet határozza meg. A φ(x, z, ω)-t ebbe helyettesítve a
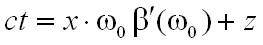 |
(14.45) |
egyenlethez jutunk, ahol kihasználtuk, hogy β0 = 0. Ez egy olyan síknak az egyenlete, amely a z-tengelyre merőleges síkkal γ szöget zár be, és amelynek a metszete a (z, x) síkban a 14.2. ábrán a kék színnel rajzolt egyenes. Ebből az egyenletből kifejezhető az
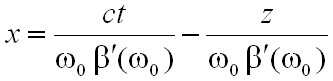 |
(14.46) |
explicit z-től való függés, ami egy egyenes egyenlete, bármely t időpontban. A meredekséget megvizsgálva látható, hogy a γ szöget a
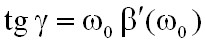 |
(14.47) |
összefüggésből számíthatjuk ki. A (14.45) egyenletből az is látható, hogy a szögdiszperzió hatására a γ szöggel megdőlt impulzusfront c sebességgel terjed a z-tengely irányába. A számolásnál β'(ω0) = 0.0748 fs és ω0 = 2.355 PHz (λ0 = 800 nm) paramétereket használtuk, amelyekből a (14.46) egyenletből kiszámítható, hogy az impulzusfront 10°-os szögben dől meg. Körfrekvenciában lineáris, azaz β(ω) = β'(ω0) (ω - ω0) típusú függést feltételezve, τ = 6 fs hosszú Gauss-os időburkolójú impulzusra a (14.44) egyenletből kiszámított, szürke skálán ábrázolt intenzitást a mellékelt animáció szemlélteti.
Az ultrarövid lézerimpulzusokat használó kísérleteknél sokszor cél a nagy teljesítmény, illetve energiasűrűség elérése [14.1-2]. Ezen célból a fényimpulzusokat lencsével vagy tükörrel fókuszálják. Fókuszálás során a beeső hullám frontját a fókuszáló optikai elem úgy változtatja meg, hogy a kilépő hullám egy adott pont (többnyire a fókuszpont) felé tartó gömbhullám lesz [14.5-6]. A fókuszáló elem hullámfrontra gyakorolt hatását vízhullámokkal végzet kísérlettel könnyen szemléltethetjük. A 14.3. ábrán egy vízhullámokat fókuszáló lencse (balra) és egy homorú tükör (jobbra) látható. A felvételeken és a kísérletekről készült filmeken egyaránt jól kivehetjük a fókuszált hullám gömb alakú hullámfrontjait. Teljesen hasonló dolog történik a fény esetében is, csak ott a hullámfrontokat közvetlenül nem látjuk. Leképezési hibák (aberrációk) jelenlétében a kilépő hullámfront az aberráció mértékétől függően eltér ettől az ideális gömb(süveg) alaktól. Az eltérés mértékét az u.n. aberráció-függvény méri [14.7].

14.3. ábra. A fókuszálás szemléltetése vízhullámokkal.
A lencse és a tükör a számolás szempontjából lényegesen nem különbözik. Mindkét eset visszavezethető egy kör alakú nyíláson áthaladó konvergens gömbhullám elhajlására. A következőkben a lencse esetét vizsgáljuk meg, a megállapítások többsége tükör esetén is érvényes. Nyílván figyelembe kell venni, hogy a kromatikus aberráció tükör esetén nem lép fel, amely egyik lehetséges oka lehet a tükrök alkalmazásának.
Tegyük fel, hogy a lencsére egy sík impulzusfronttal rendelkező, ω0 központi körfrekvenciájú, b(t) burkolóval leírható fényimpulzus esik merőlegesen. Közvetlenül a lencse előtti - a 14.4. ábrán az A - síkban a térerősség időfüggését a (14.17) egyenlet írja le. A lencse a monokromatikus komponenseket a frekvenciájukhoz tartozó fókuszpont irányába tartó konvergens gömbhullámokká alakítja át, melyek hullámfrontját a lencse nyílása kivágja. Ez alapján a probléma visszavezethető egy kör alakú nyíláson elhajló gömbhullám vizsgálatára. Ennek megfelelően a monokromatikus komponensek térerőssége a diffrakciós integrállal számítható ki [14.5-7]. A lencse mögötti térerősséget a monokromatikus komponensek szuperpozíciója szolgáltatja. A számolásnál a 14.4. ábrán vázolt vonatkoztatási rendszert használjuk. A továbbiakban a lencse anyagában való terjedés miatt fellépő impulzus-kiszélesedéstől (azaz a csoportsebesség-diszperzió hatásától), valamint a monokromatikus aberrációk okozta jelenségektől eltekintünk, vagyis az aberrációk közül csak a kromatikus aberrációt vesszük figyelembe. A lencse anyaga által okozott kiszélesedés - az erről szóló alfejezetben származtatott formulákkal - jól becsülhető. A monokromatikus aberrációk (szférikus aberráció, asztigmatizmus és kóma) hatásáról a "Femtoszekundumos optika alapjai" című tananyagban olvashat az érdeklődő. Tehát az előbb említett közelítésben - a részletekkel kapcsolatban [14.8-9] hivatkozásra utalva - a térerősséget az
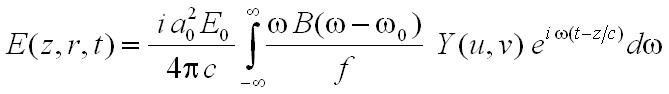 |
(14.48) |
képletből számíthatjuk ki, ahol a0 a lencse nyílásának sugara, E0 a beeső térerősség amplitúdója, B(ω) a b(t) burkoló Fourier-transzformáltja, f lencse fókusztávolsága, amely kromatikus aberráció jelenlétében függhet a körfrekvenciától,
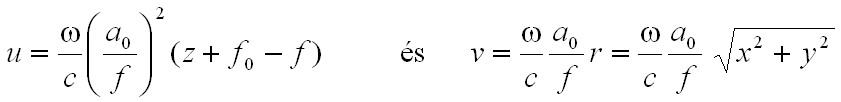 |
(14.49) |
a megfigyelési pontot megadó "optikai koordináták", melyek a z és az r térbeli hengerkoordinátáktól függenek, továbbá
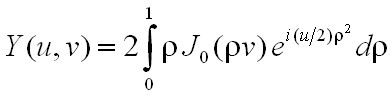 |
, | (14.50) |
ahol J0 a nulladrendű Bessel-féle függvényt jelöli. Az Y(u, v) függvény kifejezhető az U1(u, v) és az U2(u, v), illetve a V0(u, v) és az V1(u, v) Lommel-féle függvényekkel [14.6], melyek numerikusan könnyen számolhatók, mert az őket definiáló függvénysorok konvergenciája gyors [14.6].
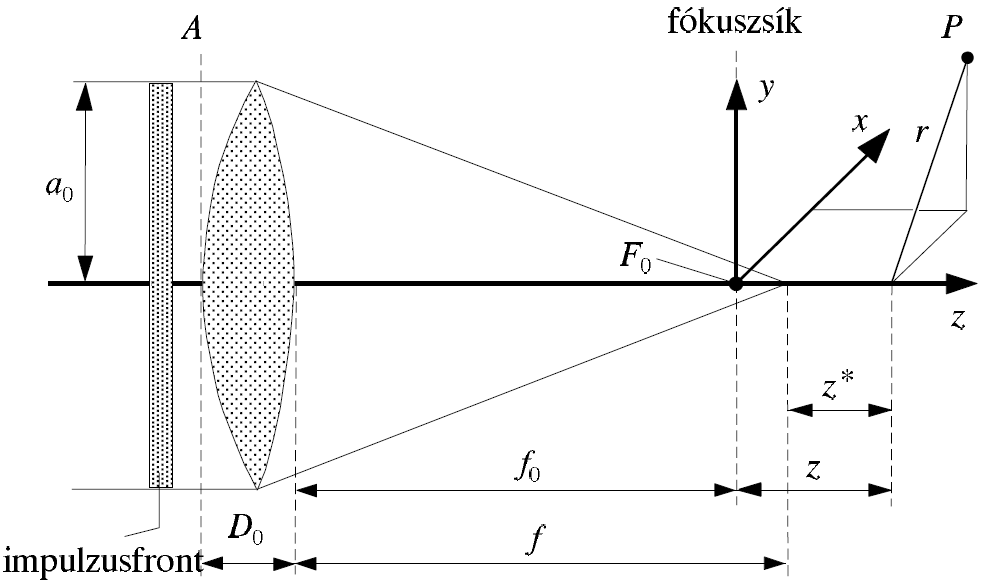
14.4. ábra. A fókuszálás leírásánál használt koordinátarendszer és a jelölések értelmezése. Az origót az ω0 központi körfrekvenciájú fókuszpontba helyezzük és a lencse optikai tengelye a z-tengely. A térerősség hengerszimmetrikus, ezért csak z és az r hengerkoordinátáktól függ.
A kromatikus aberráció hatását a következő - egyszerű geometriai optikán alapuló - modellel is vizsgálhatjuk [14.10]. A lencse anyagának diszperziója miatt, a lencsében, a 14.5. ábrán feltüntetett L2 úton, a fázis- és a csoportsebesség egymástól különböző - és a szokásos normális diszperzió esetén (dn/dλ < 0 miatt) a (14.9) és a (14.16) egyenletekből következőleg - a csoportsebesség kisebb, mint a fázissebesség. Ennek megfelelően, egy az optikai tengelytől a távolságra belépő sugár mentén (14.5. ábra) a csoportsebességgel terjedő impulzusfront lemarad a fázissebességgel terjedő - gömb alakú - az ω0 körfrekvenciájú fázisfronthoz képest.
Egyszerű számolással megmutatható, hogy a két front közötti időbeli késés
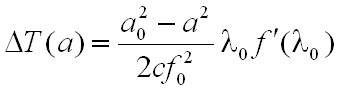 |
(14.51) |
képlettel számítható ki [14.10], ahol λ0 központi (vákuumra vonatkozó) hullámhossz, f0 az ehhez tartozó fókusztávolság. Ez alapján látható, hogy kromatikus aberráció jelenlétekor, mikor f '(λ0) nem zérus, az optikai tengelytől mért távolság négyzetével arányosan késik az impulzusfront a fázisfronthoz képest. A késés az optikai tengelyen (a = 0) a legnagyobb, és a szélső sugárra (a = a0) vonatkozólag zérus. Aberráció-mentes esetben nincs késés a két front között, vagyis erre az esetre a geometriai optikai modell gömb alakú impulzusfrontot jósol.
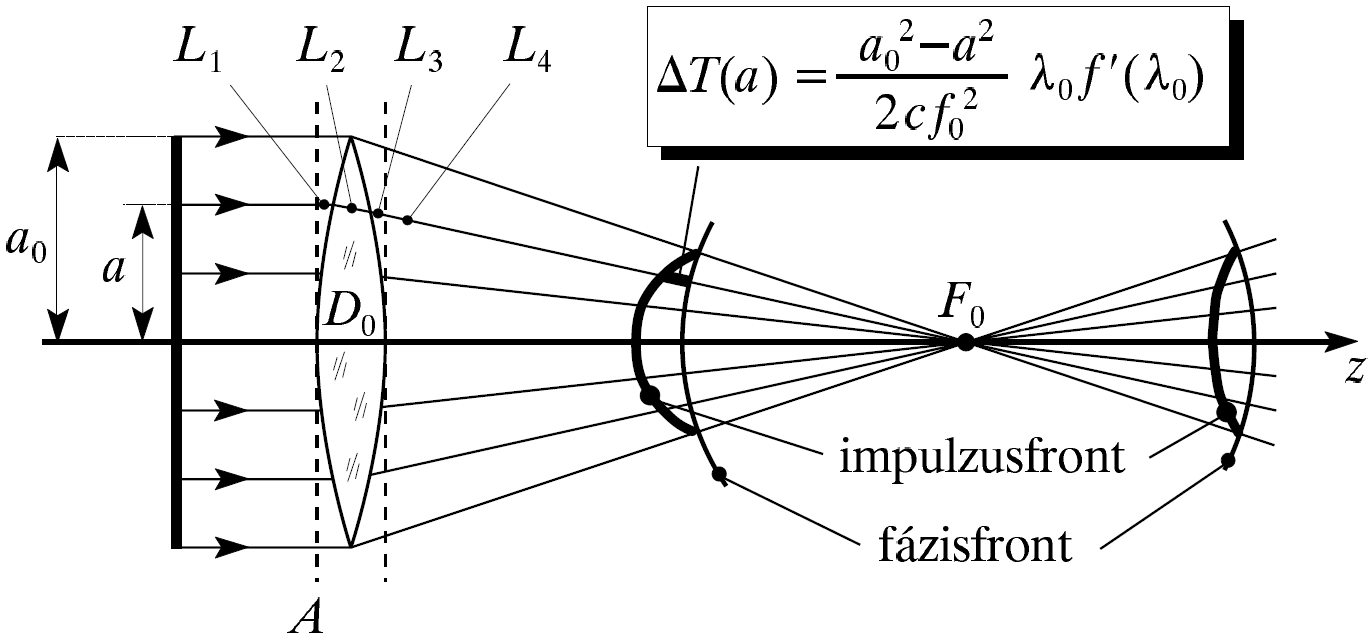
14.5. ábra. A lencsén belül a csoportsebesség kisebb, mint a fázissebesség, ezért egy adott sugár mentén a csoportsebességgel terjedő impulzusfront lemarad a gömb alakú fázisfronthoz képest.
Az egyszerű modellel kapcsolatban azonban nem szabad elfeledkezni arról, hogy a geometriai optika érvényessége éppen az alkalmazások szempontjából fontos tartományban, a fókuszpont környezetében és az árnyékhatár közelében érvényét veszti, továbbá nem tartalmazza az elhajlás és az interferencia miatt fellépő jelenségeket sem. Így a modell eredményét csak közelítésnek érdemes tekinteni és mindenképpen érdemes összevetni a diffrakcióról és az interferenciáról is számot adó hullámoptikai számolásból adódó eredménnyel. A 14.6. ábrán látható egy a0 = 40 mm sugarú, f0 = 150 mm fókusztávolságú kvarcból készült lencsén áthaladó λ0 = 249 nm központi hullámhosszúságú (n0 = 1.50799, λ0 n'(λ0) = -0.1375 és f '(λ0) = 163.0898 mm/μm) impulzus impulzusfrontjai különböző időpontokban. Az idő nullpontja úgy lett megválasztva, hogy az impulzus a tengely menti sugár mentén a t = 0 időpontban érkezik a fókuszpontba (z = 0 és r = 0).
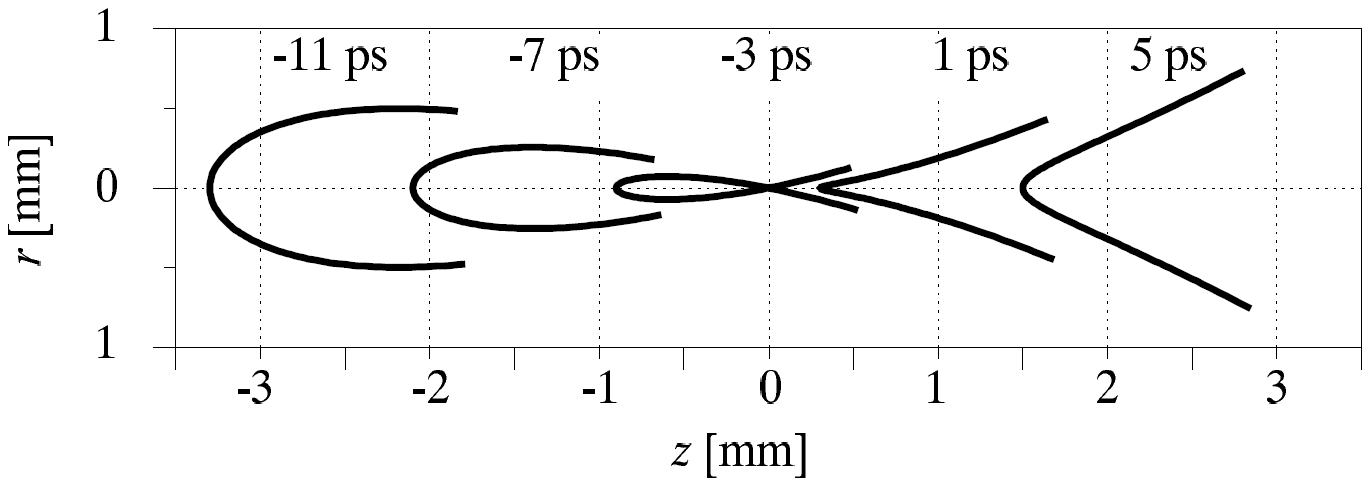
14.6. ábra. Egy f0 = 150 mm fókusztávolságú, a0 = 40 mm sugarú kvarc lencsén áthaladó λ0 = 249 nm központi hullámhosszúságú impulzus impulzusfrontjai a -11 ps, -7 ps, -3 ps, 1 ps és az 5 ps időpontokban. A -3 ps-nál is látható hurok alakú impulzusfront miatt az impulzus ΔT(0) = 4.81 ps alatt halad keresztül a fókuszon. Az impulzusfront terjedését a mellékelt animáció szemlélteti.
A kromatikus aberráció miatt, fókuszpont előtti tartományban egy lópatkóhoz hasonló alakú impulzusfront alakul ki, amely a fókuszponthoz érve "befűződik", és így egy hurok alakú impulzusfront keletkezik. A fókuszpontban először a lencse széléről, majd egyre beljebb lévő sugarak mentén érkezik fény, végül a t = 0 időpontban a tengely menti sugáron halad át az impulzus a fókuszon. Ennek következtében a fókuszpontban az impulzus időben jelentősen kiszélesedhet. A számolásnál használt lencse esetén 4.81 ps idő alatt halad át az impulzus a fókuszon. Ennek következtében például egy eredetileg 100 fs-os fényimpulzus, - melyre a szokásos lencse vastagságokra a diszperzió okozta kiszélesedés még nem jelentős - gyakorlatilag 4810 fs hosszúságúra szélesedik fókuszban. Ez a kiszélesedés természetesen jelentősen lecsökkenti az elérhető fókuszbeli intenzitást. A hullámoptikán alapuló (14.48) egyenletből számolt I = | E |2 intenzitás-eloszlás a -11 ps és 1 ps időpontokra a 14.7. ábrán látható. A számolás eredménye az mutatja, hogy a geometriai optikai modell jól írja le az impulzusfrontot (szaggatott vonal a betétábrákon). A hullámoptikai modellnek talán az egyik leginkább meglepőbb eredménye, hogy az optikai tengelyen (r = 0) egy a beeső impulzussal azonos időbeli lefutású impulzus terjed a vákuumbeli fénysebességnél nagyobb - azaz u.n. szuperluminális - sebességgel [14.8-9]. Az impulzus tulajdonságainak (például a helyének, sebességének és a radiális helyfüggésének) a vizsgálata arra utal, hogy a lencse nyílásának a peremével hozható kapcsolatba [14.8]. Valóban, a diffrakciós integrálból kiindulva, megmutatható, hogy ezen impulzus a lencse nyílásának széléről (pereméről) kiinduló elemi hullámok szuperpozíciója hozza létre, ezért ezt az impulzust szélihullám-impulzusnak neveztük el, az angol nyelvű szakirodalomban a boundary wave pulse nevet kapta. A szélihulám-impulzus a 14.7. ábrán egy kis tüskeként jelenik meg. Az számolás térbeli lépésköze nem elég finom a radiális intenzitás-eloszlás megjelenítéséhez. A radiális eloszlás a J0 Bessel-függvénnyel írható le [14.8, 14.12], és 14.9. ábrán látható.
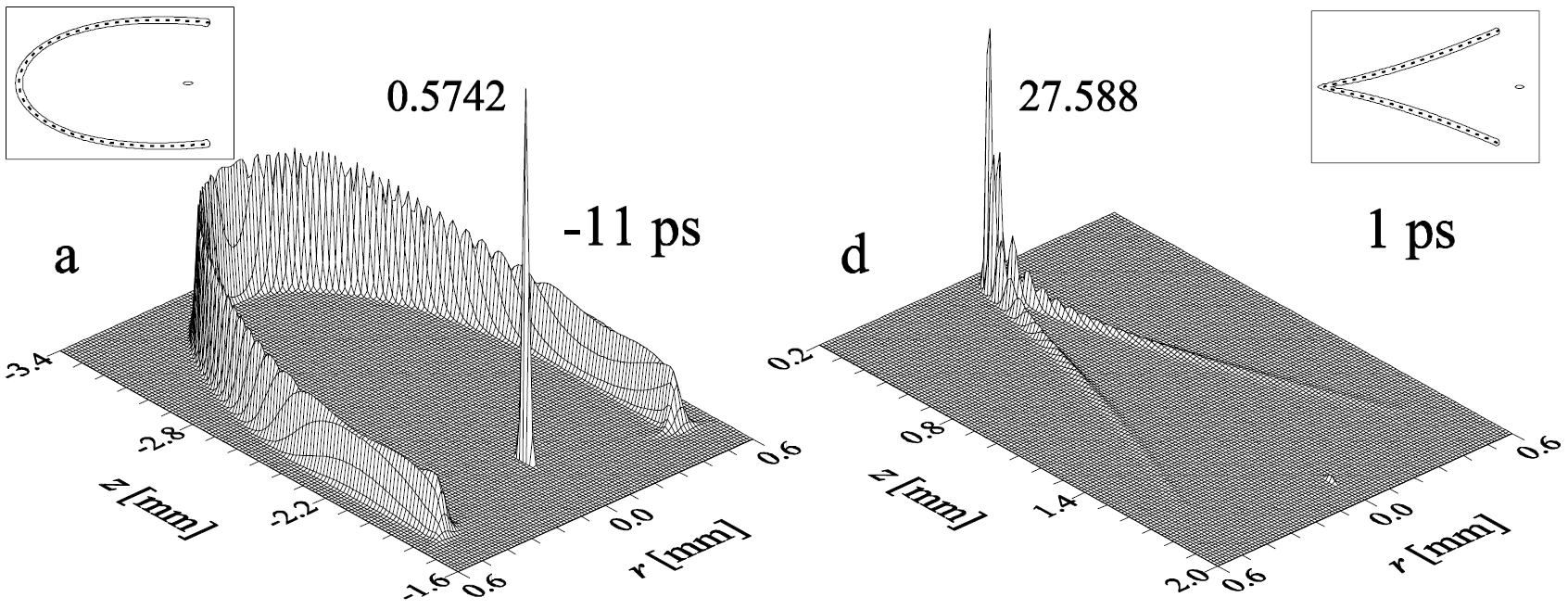
14.7. ábra. Kromatikus aberrációval rendelkező kvarc lencsén áthaladó Gauss-os időbeli burkolójú 100 fs hosszúságú, 249 nm központi hullámhosszú fényimpulzus térbeli intenzitás-eloszlása a fókuszpont előtt (balra) és után (jobbra) homogén megvilágítás esetén. A betétábrákon az intenzitás egy szintvonalát folytonos, a geometriai optikai modellből adódó impulzusfrontot szaggatott vonallal rajzoltuk fel. Az impulzus terjedését a mellékelt animáció [14.15] szemlélteti.
A fókuszsíkbeli intenzitás időfüggését a 14.8. ábra szemlélteti. Ez azt mutatja, hogy a geometriai optikai modellből kapott 4810 fs időbeli hossz a példaként vett lencsére jó becslésnek tekinthető. Homogén térbeli megvilágítás esetén (az ábrán balra) gyors felfutás és ugyanilyen lefutás között az intenzitás állandó [14.8-9], míg térben elhanyagolható csonkoltságú Gauss-eloszlású megvilágítás (vagyis Gauss-nyaláb) esetén exponenciálisan emelkedve éri el a maximumát, majd gyorsan lecsökken [14.11]. Az ábráról az is megfigyelhető, hogy a fókuszsíkban az intenzitás-eloszlás egy időben növekvő sugarú, világos-sötét mintázatú, középen világos foltot tartalmazó, koncentrikus interferencia-gyűrűrendszer.
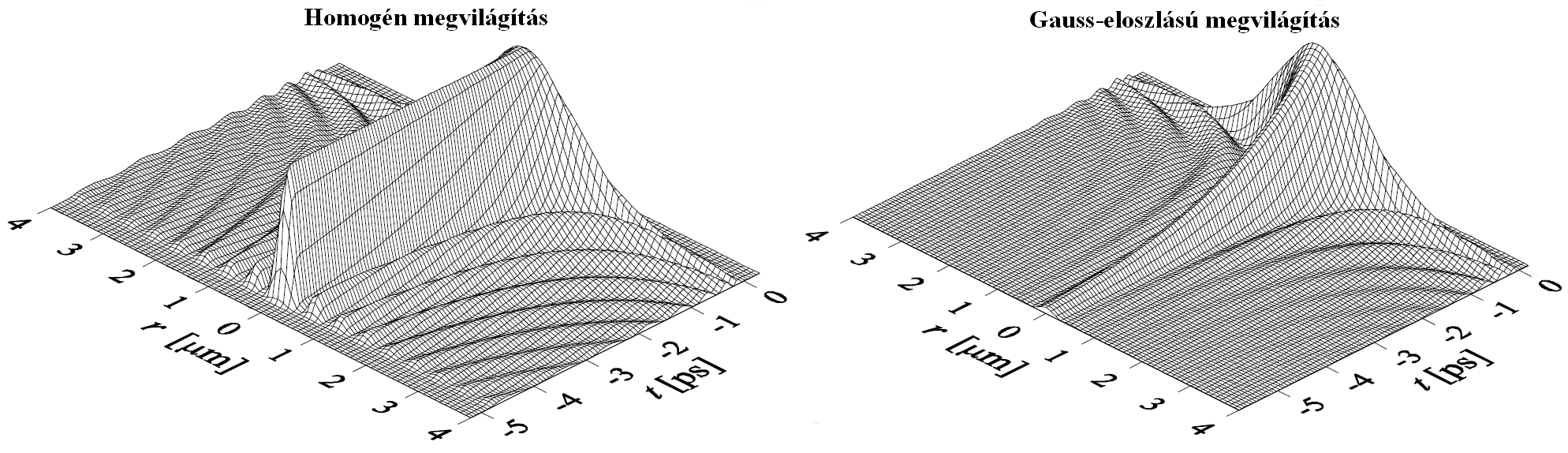
14.8. ábra. Kromatikus aberrációval rendelkező kvarc lencsén áthaladó Gauss-os időbeli burkolójú 100 fs hosszúságú, 249 nm központi hullámhosszú fényimpulzus intenzitásának az időfüggése a fókuszsíkban (z = 0) a lencsének térben homogén illetve Gauss-eloszlású megvilágítása esetén.
Aberrációk hiányában a (14.48) egyenletből számolt intenzitás-eloszlást szemlélteti a 14.8. ábra. A geometriai optikai modellből számolt impulzusfrontot szaggatott vonal jelöli. Látható, hogy a szélihullám-impulzus akromát lencse esetén is megjelenik. Aberrációmentes esetben a fókuszpont előtt a gömbsüveg alakú impulzusfront megelőzi, a fókuszpont után lemarad a szélihullám-impulzushoz képest, ahogy az a 14.9. ábrán is látszik, és a mellékelt animáción is látható. A diffrakciónak van egy - eredetileg még Thomas Youngtól származó - értelmezése [14.12], amely szerint az elhajlás során a nyílás mögötti hullám előáll a nyíláson zavartalanul tovaterjedő és a nyílás pereme által generált szélihullám szuperpozíciójaként. Megmutatható, hogy a Fresnel-féle értelmezést matematikai megfogalmazásának tekinthető diffrakciós integrál valóban szétbontható két ilyen hullám összegére [14.12]. Az animáción a nyíláson áthaladó és zavartalanul tovaterjedő konvergens gömbhullámot piros, míg a nyílás pereméről kiinduló hullámot kék szín szemlélteti. A lencse pereme által generált szélihullámok vízhullámokkal végzett kísérletben jól megfigyelhetők. Rövid impulzusok esetén a zavartalanul terjedő hullám és a szélihullám, pontosan a rövid impulzushossz miatt, gyakran térben elkülönülten jelenik meg. Az elhajlásnak a Young-féle értelmezés ezért rövid impulzusok esetén sokszor szemléletesebb, vagyis könnyebben értelmezhetőbb, mint a Fresnel-féle értelmezést használva.
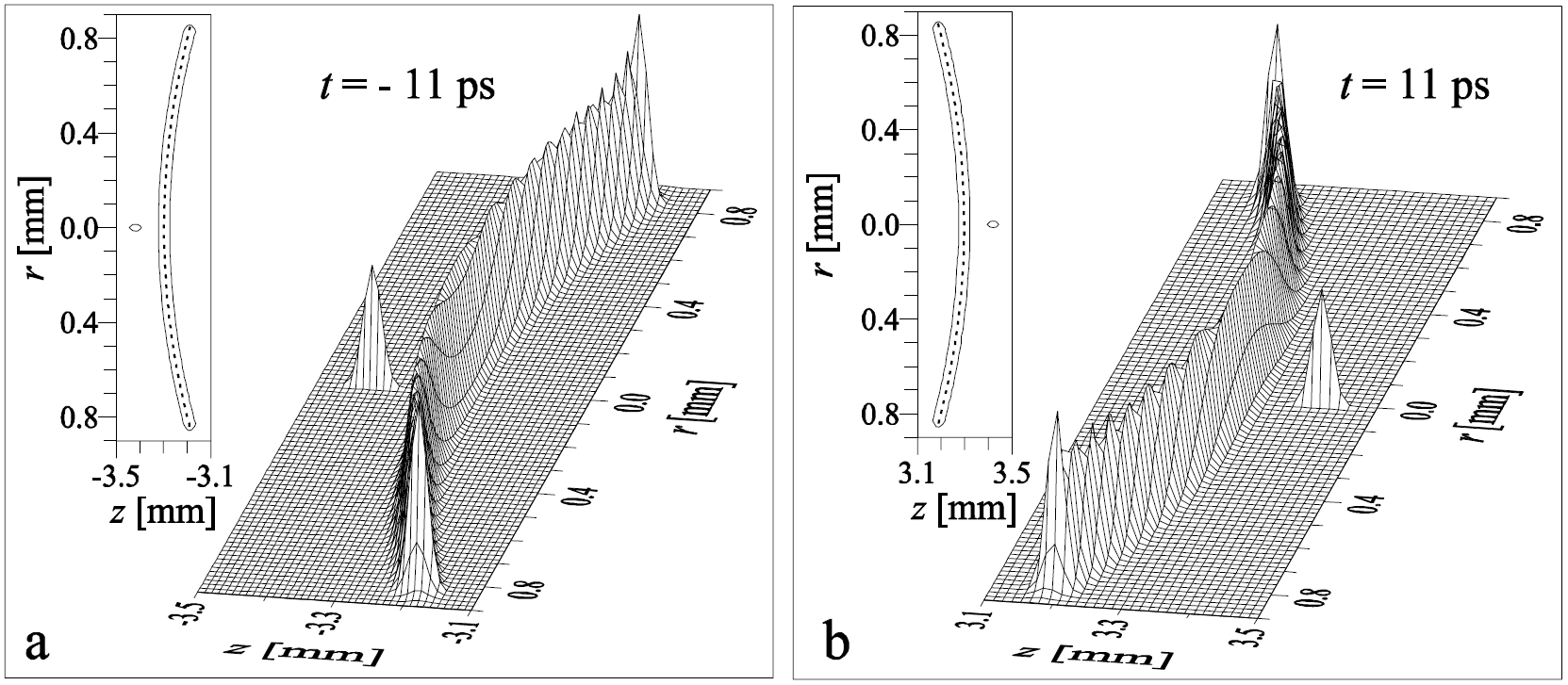
14.9. ábra. Akromatikus lencsén áthaladó Gauss-os időbeli burkolójú 100 fs hosszúságú, 249 nm központi hullámhosszú fényimpulzus térbeli intenzitás-eloszlása a fókuszpont előtt (balra) és mögött (jobbra) homogén megvilágítás esetén. A betétábrákon az intenzitás egy szintvonalát folytonos, a geometriai optikai modellből adódó impulzusfrontot szaggatott vonallal rajzoltuk fel. Az impulzus terjedését a mellékelt animáció [14.15] szemlélteti
A szélihullám-impulzus radiális eloszlását a 14.10. ábra mutatja. Érdemes megemlíteni, hogy a szélihullám-impulzus létét kísérletileg többféle módszerrel is igazolták [14.13-14]. A számolások és a mérések között jó egyezés van.
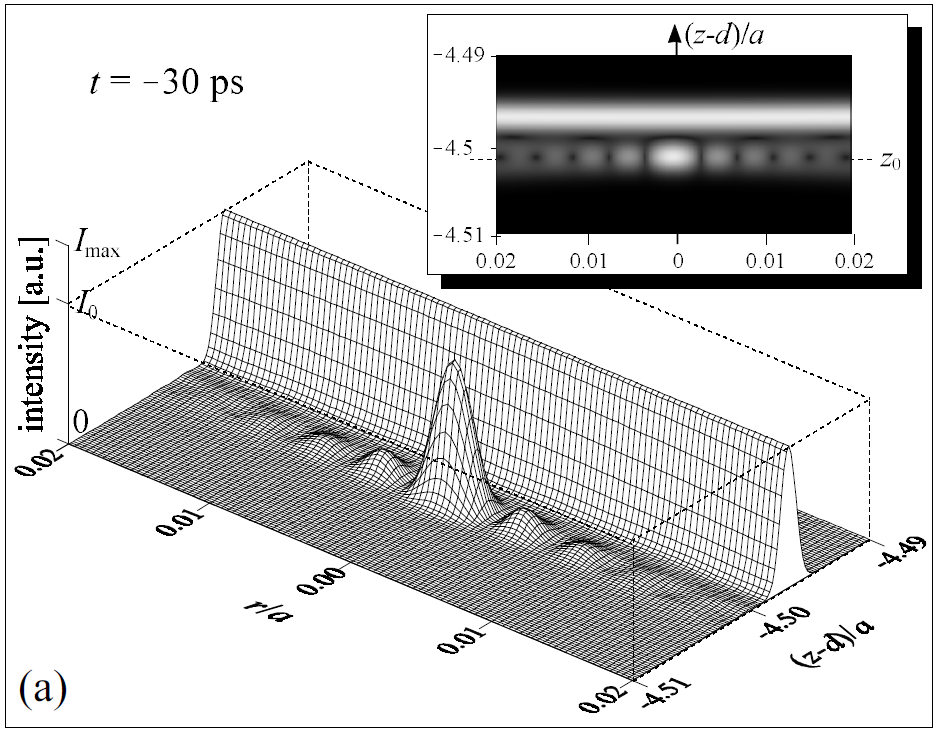
14.10. ábra. A szélihullám-impulzus radiális eloszlása. [14.12].
Milyen hatása van a közeg diszperziójának egy rövid impulzus terjedésére?
Milyen hatása van a szögdiszperziónak egy rövid impulzus terjedésére?
Hogyan számítható egy n törésmutatójú közegben azonos irányba terjedő monokromatikus síkhullámok szuperpozíciójaként kialakuló impulzusra a csoportsebesség?
Az előző esetre vonatkozólag, mikor kisebb, illetve nagyobb a csoportsebesség, mint a központi frekvenciához tartozó fázissebesség?
Hogyan befolyásolja a kromatikus aberráció egy fókuszált rövid impulzusfrontját?
Mit jelent a szuperluminális szó?
[14.1] J. C. Diels and W. Rudolph, Ultrashort Laser Pulse Phenomena, (Academic Press, 2nd edition).
[14.2] A. M. Weiner, Ultrafast Optics, (Wiley)
[14.3] M. Born and E. Wolf, Principles of Optics, chapter 1.3.3 (Cambridge University Press, 7th edition).
[14.4] M. Born and E. Wolf, Principles of Optics, chapter 1.3.4 (Cambridge University Press, 7th edition).
[14.5] J. W. Goodman, Introduction to Fourier Optics (McGraw-Hill Book Company, 1968), chapter. 2-3.
[14.6] M. Born and E. Wolf, Principles of Optics, chapter 8.8 (Cambridge University Press, 7th edition).
[14.7] M. Born and E. Wolf, Principles of Optics, chapter 9 (Cambridge University Press, 7th edition).
[14.8] Zs. Bor, Z. L. Horváth, Distortion of Femtosecond Pulse in Lenses. Wave Optical Description, Optics Commun. 94 (1992) 249-258.
[14.9] Z. L. Horváth and Zs. Bor, Behaviour of Femtosecond Pulses on The Optical Axis of a Lens. Analytical Description, Optics Commun. 108 (1994) 333-342.
[14.10] Zs. Bor, Distortion of femtosecond laser pulses in lenses and lens systems, J. Mod. Opt. 35 (1988), 1907.
[14.11] Z. L. Horváth, Zs. Bor, Focussing of Femtosecond Pulses Having Gaussian Spatial Distribution, Optics Commun. 100 (1993) 6-12.
[14.12] Z. L. Horváth and Zs. Bor, Diffraction short pulses with boundary wave theory, Phys. Rev. E 63 (2001) 26601.
[14.13] Z. L. Horváth, J. Klebniczki, G. Kurdi and A. P. Kovács, Experimental investigation of boundary wave pulse, Optics Commun. 239 (2004) 243.
[14.14] P. Saari, P. Bowlan, H. Valtna-Lukner, M. Löhmus, P. Piksarv and R. Trebino, Basic diffraction phenomena in time domain, Opt. Express 18 (2010) 11083-8.
[14.15] U. Fuchs, U. D. Zeitner and A. Tünnermann, Ultra-short pulse propagation in complex optical systems, Optics Express 13 (2005) 3852.
Tartalom
Egy adott lézer alkalmazhatósága szempontjából fontos, hogy ismerjük az alábbi paramétereit:
A lézerek működése során az egyik legfontosabb paraméter, amit mérésekkel rendszeresen ellenőriznünk kell, a folytonos üzemű lézereknél a teljesítmény, míg az impulzus üzemű lézereknél az impulzusok energiája illetve a lézer átlagteljesítménye [15.1,15.2]. Mielőtt a mérési módszerekre rátérnénk, először tekintsük át az impulzusenergia (E), az impulzus intenzitásban mért időbeli félértékszélessége (τ), a lézer ismétlési frekvenciájája (fism), a csúcsteljesítmény (Pcsúcs) illetve az átlagteljesítmény (Pátl) közötti kapcsolatot. Impulzus üzemű lézer esetében a lézer csúcsteljesítménye egy impulzus energiája és az impulzus időtartamának hányadosaként áll elő, azaz
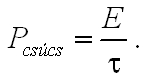 |
. | (15.1) |
Látható, hogy a csúcsteljesítmény fordítva arányos az impulzus időtartamával, azaz ha rövidítjük az impulzus időtartamát, akkor ugyanazon impulzusenergia mellett jóval nagyobb csúcsteljesítmény érhető el. Az impulzuslézer átlagteljesítménye az alábbi
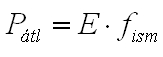 |
. | (15.2) |
összefüggés alapján számolhatjuk ki.
Ahhoz, hogy fogalmunk legyen arról, hogy a lézerek esetében milyen nagyságrendet jelent az átlag- illetve a csúcsteljesítmény, tekintsünk példaként egy excimer lézert, mely 10 ns időtartamú, 10 mJ energiájú impulzusokat bocsát ki 10 Hz ismétlési frekvenciával. Ekkor a lézer csúcsteljesítménye
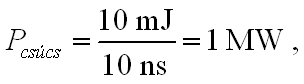 |
(15.3) |
míg a lézer átlagteljesítménye:
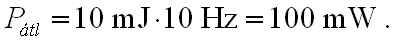 |
(15.4) |
Ezután tekintsünk egy másik példát, egy ultrarövid impulzusokat előállító lézert. Egy 6 fs impulzusokat, 70 MHz ismétlési frekvenciával kibocsátó, 210 mW átlagteljesítményű Ti:zafír lézer esetében az impulzusenergia csak
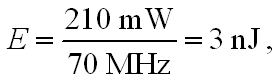 |
(15.5) |
miközben a csúcsteljesítmény
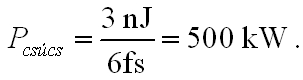 |
(15.6) |
Összehasonlítva a két lézert, miközben a Ti:zafír lézer impulzusainak csúcsteljesítménye fele az excimer lézerének, addig az impulzusenergia esetében a Ti:zafír lézer impulzusának energiája csak 3 milliomod része az excimer lézerének. Ha például orvosi diagnosztikában humán vizsgálatra keresünk lézert, ahol fontos szempont, hogy minél kisebb energiabesugárzás érje a beteget, miközben a detektált jel szempontjából az az előnyös, hogy a lézerimpulzusok minél nagyobb csúcsteljesítménnyel bírjanak, akkor a fenti példák alapján a femtoszekundumos lézer egy jó választás.
A lézerek energiájának illetve teljesítményének mérésére használt detektorokat két fő csoportba oszthatjuk, termikus és kvantumos detektorokra. A termikus detektorok abszorbeálják a lézersugárzást, aminek hatására megnő a detektor elemeinek hőmérséklete. A hővezetés és a hősugárzás okozta hőveszteség, valamint a beérkező sugárzás hatására kialakuló hőmérsékleti egyensúlynál a kialakult hőmérsékletből meghatározható a lézernyaláb teljesítménye. A termikus detektorok két típusra oszthatók tovább, piroelektromos detektorokra és termooszlopokra. A piroelektromos detektorokat az impulzuslézereknél az impulzusok energiájának mérésére, míg a termooszlopokat a folytonos lézerek teljesítményének mérésére használják. Mivel a termikus detektorok csak a detektorban keletkezett hőt mérik, így igen széles hullámhossztartományban használhatók, tipikusan 200 nm és 20 μm között lényegében állandó az érzékenységük.
A kvantumos detektorok teljesen más elven működnek. A detektor anyaga egy félvezető, melyben a lézersugárzásból elnyelt fotonok a félvezetőnek a vegyértéksávjában lévő elektronjait a vezetési sávba gerjesztve áramot generálnak. Az áram erőssége arányos a beérkező sugárzásban lévő fotonok számával. Csak azok a fotonok tudják az elektronokat gerjeszteni, amelyeknek az energiája nagyobb vagy egyenlő a vegyérték- és a vezetési sáv közötti Eg energiakülönbséggel, azaz a hullámhosszuk maximális értéke:
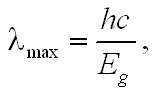 |
(15.7) |
ahol c a félvezetőben a fénysebesség értéke, és a h a Planck-állandó. A kvantumos detektorok is két csoportra oszthatók, fotodiódákra és fotovezetőkre. Míg az utóbbi detektortípus elsősorban a közeli infravörös hullámhossztartományban kb. 5 μm-ig, addig a fotodiódák a látható és az ultraibolya tartományban érzékenyek.
Összehasonlítva a kvantumos és a termikus detektorok jellemzőit megállapíthatjuk, hogy a kvantumos detektorok érzékenysége sokkal nagyobb, akár pW-os teljesítmények is mérhetők velük. Továbbá a válaszidejük sokkal kisebb, mint a termikus detektoroké. Ami viszont a spektrális érzékenységet illeti, a kvantumos detektoroknak az érzékenysége erősen függ a hullámhossztól ellentétben a termikus detektorokkal, és sokkal kisebb hullámhossztartományon használhatók. További hátrányuk a kvantumos detektoroknak, hogy sérülékenyebbek, ezért nagy teljesítményű lézereknél nagy körültekintést igényel a használatuk.
A termooszlopok több sorba kapcsolt termoelemből tevődnek össze (15.1 ábra). A termoelemek két különböző anyagi minőségű fémszálból állnak, melyeket egyik végüknél összeforrasztanak. A másik, szabad végeiket egy állandó hőmérsékletű hőtartályba teszik. A termoelemek forrasztási pontjait a teljesítménymérő abszorber rétege mögé helyezik el közvetlenül. Amint az abszorbert megvilágítja a lézernyaláb, az elnyelt fényenergia hatására felmelegszik. Ezáltal a mögötte elhelyezett termoelem kontaktusa is felmelegszik, és mivel a forrasztási pont és a termooelemet alkotó két fémszál szabad vége között hőmérsékletkülönbség alakul ki, így a szabad végek között feszültség, termofeszültség jön létre. A termofeszültség értéke arányos a termoelem két vége közötti hőmérsékletkülönbséggel. Mivel sorba vannak kapcsolva a termoelemek, így a keletkezett termofeszültségek összeadódnak. A detektorhoz kapcsolódó mérőegység feladata, hogy a mért feszültséget teljesítmény vagy energiaértékre konvertálja át, és jelezze ki.
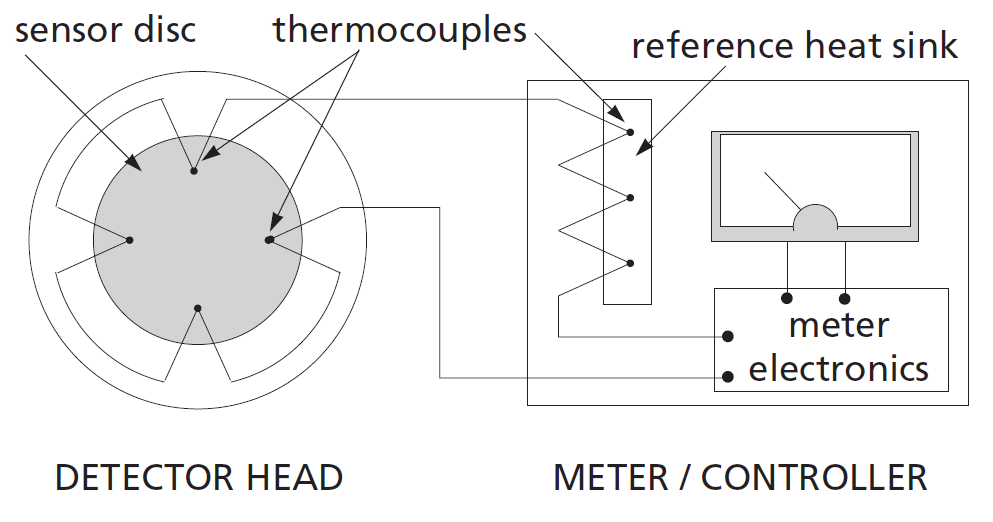
15.1 ábra. Termooszlop kapcsolási rajza [15.2].
Az abszorber réteg tipikusan grafit vagy lefeketített alumínium tömb. A abszorber felületén elnyelt energiának idő kell ahhoz, hogy az egész tömbben szétterjedjen, és kialakuljon az állandó hőmérséklet. Nagyobb tömegű tömb esetén, melyeket nagyteljesítményű lézereknél használnak, ez az idő akár néhány másodperc is lehet, míg kisebb tömböknél csak a másodperc törtrésze. Ellensúlyozandó a detektor lassú válaszidejét, a gyártók számos esetben egy olyan áramkört is beépítenek, mely mérés közben vizsgálja a hőmérséklet emelkedésének ütemét, és megbecsüli a termikus egyensúlyhoz tartozó hőmérséklet értékét. A lassú válaszidő miatt a termooszlopokat elsősorban a folytonos üzemű lézerek teljesítményének illetve az impulzusüzemű lézerek átlagteljesítményének mérésére használják. Impulzusok csúcsteljesítményének vagy energiájának mérése ezzel a detektorral 1-2 Hz-nél nagyobb ismétlési frekvencia esetén problematikus.
Amikor egy piroelektromos tulajdonsággal bíró kristályt melegítünk, a kristály két, egymással szemben lévő oldalán felületi töltések jelennek meg. Ennek eredményeképp a két oldal között feszültség alakul ki, melynek nagysága arányos az elnyelt energiával. A detektorhoz kapcsolt mérőegység vagy a felületi töltésmennyiséget, vagy a feszültséget méri, és ennek alapján kijelzi az impulzus csúcsteljesítményét vagy energiáját megadó számértéket. A termooszloptól eltérően termikus egyensúlynál a felületi töltések és a kristály két lapja közötti feszültség is eltűnik, így ez a detektor nem használható folytonos üzemű lézerek esetében. Ha a detektor mérőegysége a kristályban kialakuló feszültséget méri, akkor csak alacsony (<10 Hz) ismétlési frekvenciájú lézereknél használható, ugyanis idő kell ahhoz, hogy az elnyelt energia szétterjedjen a kristályban. Ellenben ha a felületi töltéseket méri, akkor 1 kHz-nél nagyobb ismétlési frekvenciánál alkalmazható, mivel itt a fontos tényező a lézersugárzás által megvilágított detektorfelület hőmérséklete.
A fotovezető detektorok erősen szennyezett félvezetők, amelyeknek a véges vezetőképessége növekszik a hőmérséklettel. Ezeket elsősorban az infravörös sugárzás detektálására használják. A detektort előfeszítik egy adott feszültséggel, és a detektoron átfolyó áram adja a mérendő jelet. Egy komoly problémája e detektoroknak, hogy a környező hőmérséklet kicsiny megváltozása is jelentősen megnöveli a sötétáramot, ami torzítja a jelet. Kiküszöbölni úgy lehet ezt a hatást, hogy vagy stabilizálják a detektor hőmérsékletét, vagy csak fázisérzékeny mérésre használják.
A fotodiódák esetében a záróirányban előfeszített dióda p-n átmenetében elnyelt lézerfény fotonjai konvertálódnak át árammá, amit mérni tudunk. Az e célra használt fotodiódák nagy érzékenységűek és kicsiny a zajuk, így nagyon alacsony fényteljesítmények is mérhetők velük. Ha mW-nál nagyobb teljesítményű lézernyaláb útjába helyezzük, akkor fényszűrőt kell a dióda elé tenni, hogy elkerüljük a telítődését. A fotodiódáknak gyors a válaszideje, akár szubnanoszekundumos nagyságrendbe is eshet, így jól használhatók a lézerek beállításánál valamint nanoszekundumos lézerimpulzusok időbeli alakjának direkt mérésére. A vizsgálható hullámhossztartomány az előbb tárgyalt termooszlopokkal ellentétben kisebb. A szilícium fotodiódákkal a 400-1100 nm-es tartomány (15.2.a ábra), míg germánium diódákkal a 800-1800 nm-es tartomány vizsgálható (15.2.b ábra).
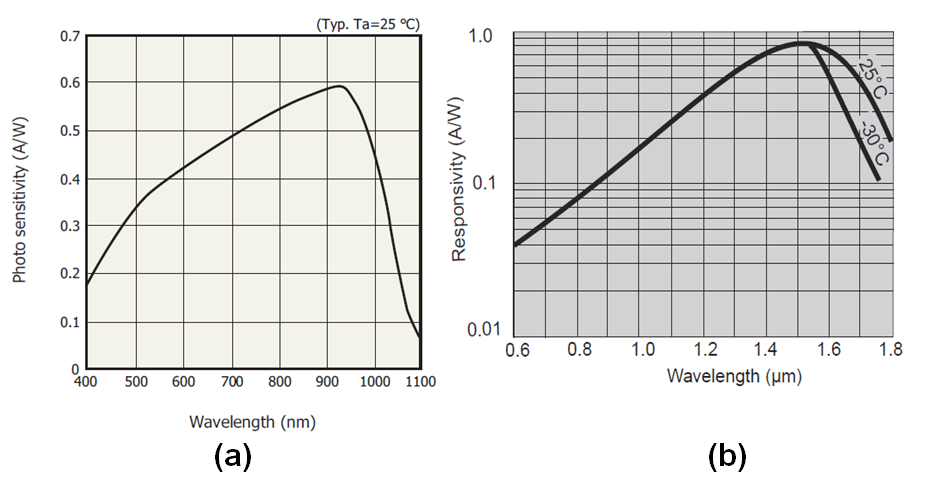
15.2. ábra Fotodiódák spektrális érzékenységi görbéje (a) szilícium fotodióda [15.3], (b) germánium fotodióda esetében [15.4].
A termooszlopokhoz képest néhány nagyságrenddel nagyobb az érzékenységük. A fotodiódákat abban az esetben érdemes használni, ha a lézerteljesítménye nW-mW tartományban van. Összefoglalásképpen az 15.1. táblázatban áttekinthetjük, hogy a különböző lézertípusoknál mely detektort ajánlott alkalmazni.
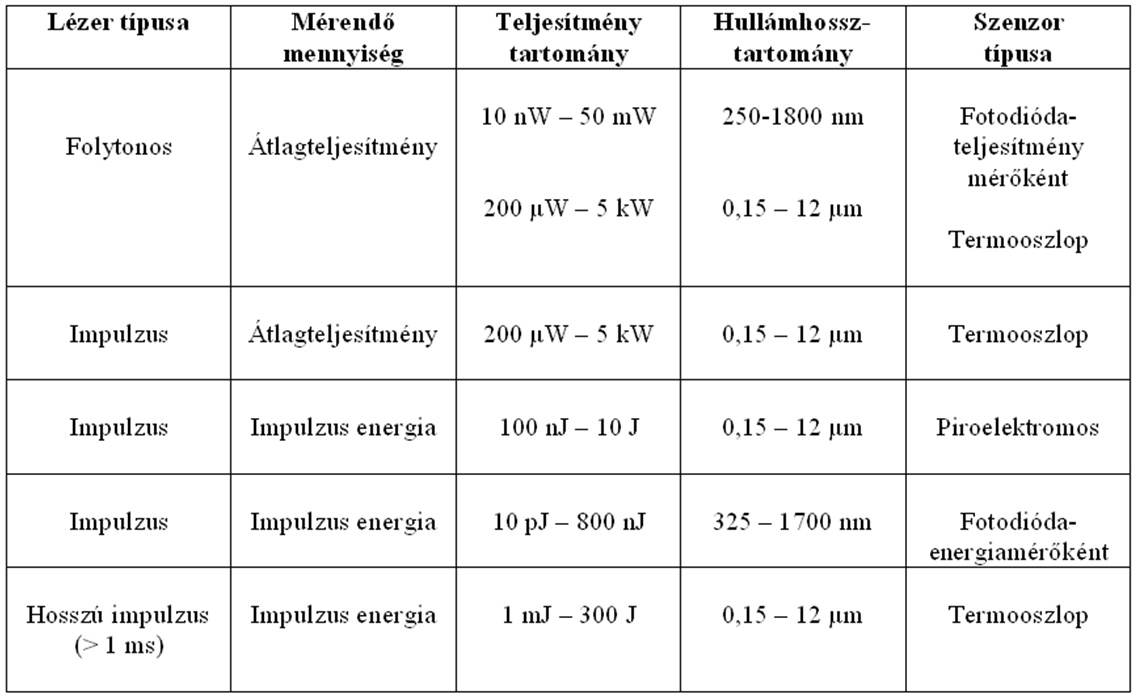
15.1. táblázat. A különböző lézerek energiájának illetve teljesítményének mérésére használható detektorok [15.1].
Ha egy rövidimpulzusú lézer spektrumát akarjuk megmérni, melynek a spektruma az ultraibolyától a közeli infravörös hullámhosszakig tartó tartományba esik, akkor erre a legáltalánosabban használt mérőeszköz a rácsos spektrométer (15.3 ábra). A rácsos spektrométerek felépítése az elvárt felbontóképességtől, a vizsgált hullámhossztartománytól függően kissé eltérő lehet az ábrán láthatótól.
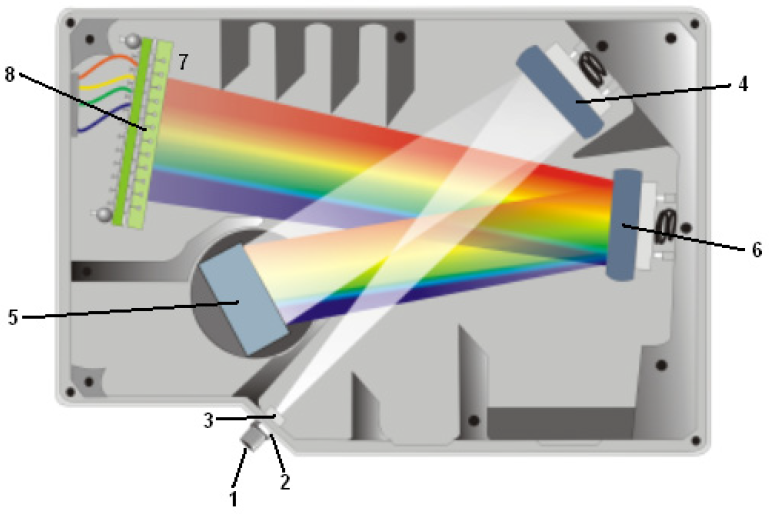
15.3. ábra. Az Ocean Optics cég HR4000-es rácsos spektrométerének felépítése. 1: SMA végződésű optikai szál csatlakozója, 2: optikai rés, 3: színszűrő, 4: kollimáló tükör, 5: reflexiós optikai rács, 6: fókuszáló tükör, 7: didódasor (detektor) [15.5].
A vizsgálandó lézerfény közvetlenül is ráfókuszálható a spektrométer belépő résére, de egy optikai szálon is odavezethető. Ebben az esetben csak SMA végződésű szál csatlakoztatható a spektrométerre. A résből kilépő divergens nyalábot egy homorú tükörrel párhuzamosítjuk, és ráirányítjuk a reflexiós rácsra. A rács a lézerfényben előforduló különböző hullámhosszú komponenseket különböző irányba téríti el. A rács után elhelyezett homorú tükör a szétválasztott spektrális komponenseket ráfókuszálja a detektorra, ami egy diódasor. Ha a vizsgált hullámhossztartomány a 300-1100 nm közé esik, akkor Si-diódasort használunk, míg ha 900-1700 nm közé, akkor InGaAs anyagú diódasort. Míg a Si-diódasor akár 3648 pixelből, addig a technikai nehézségek miatt az InGaAs diósasor rendszerint csak 512 pixelből áll. Ebből következően az infravörös tartományban ezekkel a spektrométerekkel elérhető spektrális felbontás nem túl nagy (1-3 nm). Ha viszont a látható tartományban működik a lézer, ott 0,05-1 nm közötti felbontást kapunk.
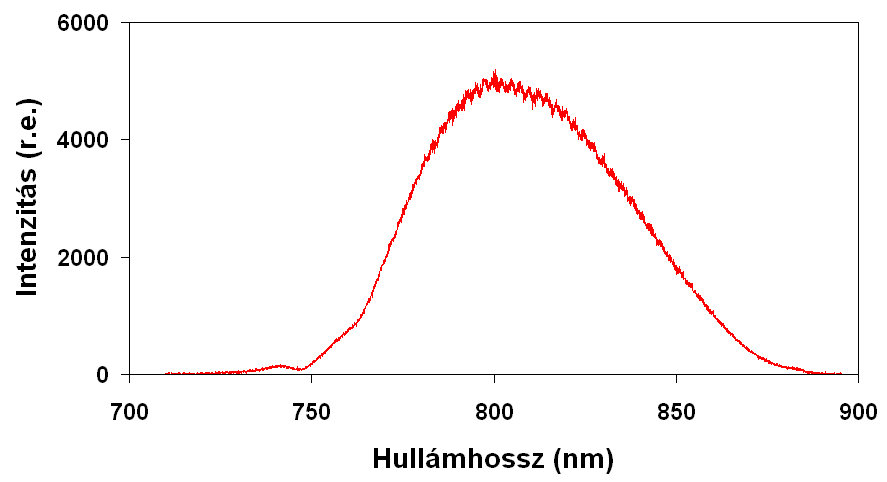
15.4. ábra. Egy Ti:zafír lézer spektruma a HR4000-es spektrométerrel mérve.
A 15.4 ábrán egy 15 fs-os impulzusokat kibocsátó Ti:zafír lézer spektruma látható, mely egy Ocean Optics HR4000 spektrométerrel készült. Figyelni kell arra, hogy a spektrométer spektrális érzékenységi görbéje kalibrált-e, mert ha nem, akkor a pontos spektrum meghatározásához egy feketetest sugárzóval el kell végeznünk a kalibrációt is.
Ha az infravörös hullámhossztartományban jobb spektrális felbontást szeretnénk, akkor egy Fourier-transzformációs spektrométert kell használnunk, ami alapvetően egy Michelson interferométerre épül (15.5 ábra). Kismértékben előre-hátra mozgatva az interferométer egyik
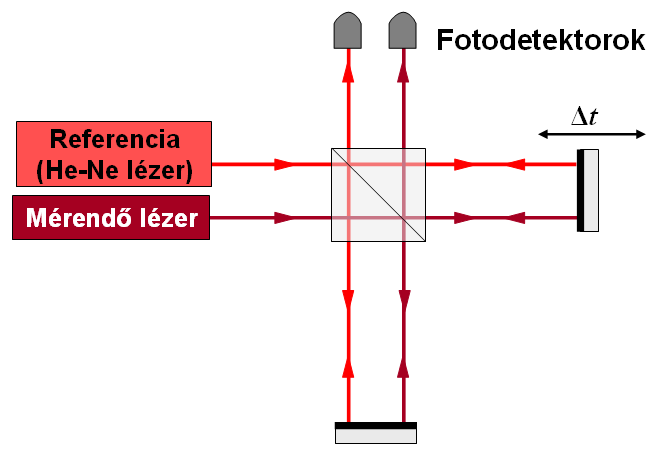
15.5. ábra. Fourier-transzformációs spektrométer elvi felépítése.
tükrét, az interferométer kimenetén elhelyezett fotodióda jelét felvesszük. A jelet Fourier-transzformálva, kimutatható, hogy éppen a lézerfény spektrumát kapjuk meg. Szükségünk van egy monokromatikus referenciafényforrásra, esetünkben egy HeNe lézerre, amelynek a jelét detektálva, meg tudjuk pontosan határozni a késleltetés mértékét a különböző időpillanatokban. Ebben az esetben nincsen sem rés, sem bontóelem, mint a rácsos spektrométernél, így itt a spektrális felbontást a tükör mozgatásával az interferométer két karja között okozott Δt időkülönbség nagysága határozza meg. Minél nagyobb időkésleltetést okozunk, annál jobb lesz a felbontás.
Ha lézer spektruma nagyon vékony, 1-2 nm vagy annál kisebb, akkor Fabry-Perot interferométer használható a spektrum meghatározására. Különösen a konfokális pásztázó Fabry-Perot interferométert alkalmazzák e célra (15.6. ábra). Az interferométer két homorú tükörből áll, melyek egymással szembe vannak fordítva, és a fókuszpontjuk egybeesik. A tükör bevonata olyan, hogy a reflexiója közel 100 %-os. (Ekkor a legjobb az interferométer spektrális felbontóképessége.) A mérendő lézerfénnyel keresztülvilágítunk az interferométeren, mely után egy fotodetektort helyezünk el. Egy piezoeltolóval finoman változtatjuk a két tükör közötti d távolságot, és közben felvesszük a detektorral az interferométerből kilépő fény intenzitását.
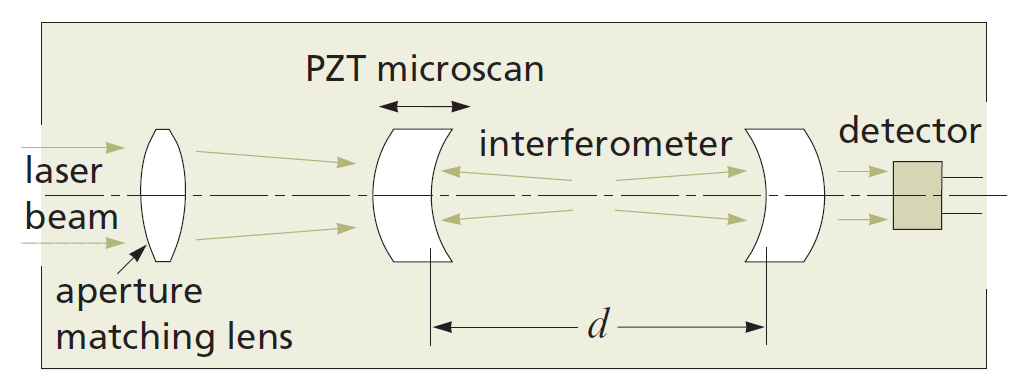
15.6. ábra. Pásztázó konfokális Fabry-Perot interferométer lézerfény spektrumának meghatározására [15.2].
A 15.7. ábrán látható a kapott jel, amikor a lézer két longitudinális módusban működik. Vegyük észre, hogy a jelalak ismétlődik, ami a Fabry-Perot interferométer jellemzője, ha változtatjuk a bázistávolságát.
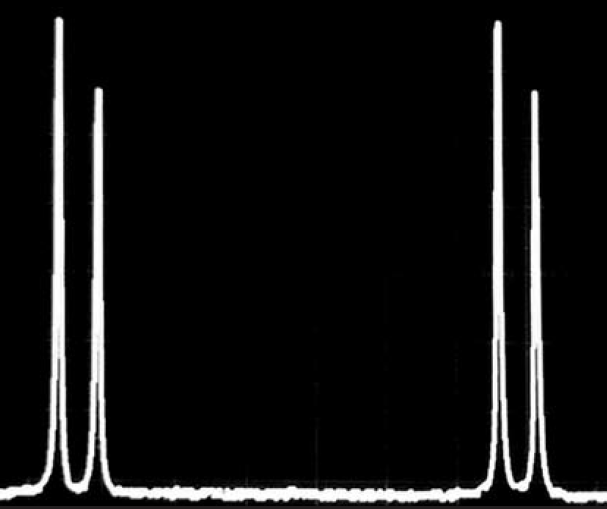
15.7. ábra. Két módusú lézerműködés esetén kapott spektrum [15.2].
Ha tudjuk, hogy a vizsgálandó lézerünk monokromatikus fény bocsát ki, akkor a 15.5. ábrán látható elrendezés használható a hullámhosszának meghatározására. Ebben az esetben nem kell Fourier-transzformálni a mért jelet, pusztán csak össze kell hasonlítani, hogy adott Δt időbeli késleltetés alatt hány periódus van a referencia illetve a mérendő lézerrel kapott jelben. A kettő hányadosa megegyezik a két lézer hullámhosszának hányadosával.
A lézerimpulzus időbeli alakjának meghatározására alkalmazott módszerek attól függnek, hogy az impulzus időbeli hossza nanoszekundumnál nagyobb vagy kisebb. Ha nagyobb, akkor a mérés egyszerű, mert a lézernyaláb útjába helyezünk egy fotodiódát, és a fotodióda jele megegyezik az impulzus intenzitásának időbeli alakjával. Pontosabban ez csak akkor igaz, ha az impulzus időtartama jóval nagyobb, mint a fotodióda tipikusan ns körüli válaszjele. Ha viszont a két időtartam hasonló nagyságrendű, akkor a Fourier-transzformáción alapuló dekonvolúciós eljárást alkalmazva tudjuk a fotodióda jeléből visszaszámolni az impulzus időbeli alakját.
Ha az impulzus időtartama 1-100 ps között van, akkor használhatjuk a sávkamerát. Ez az eszköz egy olyan oszcilloszkóphoz hasonlít, amelyiknek az egyik nyalábeltérítő egységét kivettük. A másik egységnél pedig az eltérítés gyorsaságát megnöveltük (15.8. ábra).
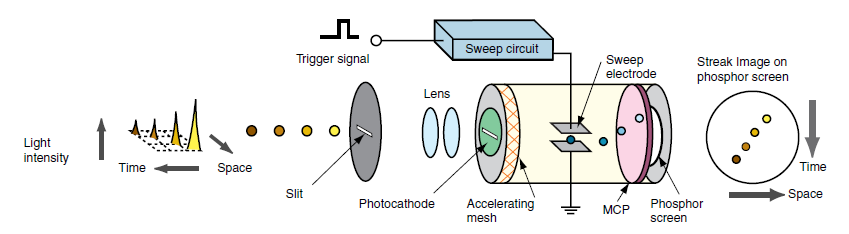
15.8. ábra. Sávkamera elvi felépítése [15.6].
Az impulzus időbeli alakját a kamera eltérítő egysége térbeli alakra konvertálja át azáltal, hogy miközben az impulzus keresztülhalad az egységen, az eltérítés mértéke folyamatosan változik. Manapság már kapható 200 fs-os időbeli felbontású sávkamera [15.6] (15.9. ábra).
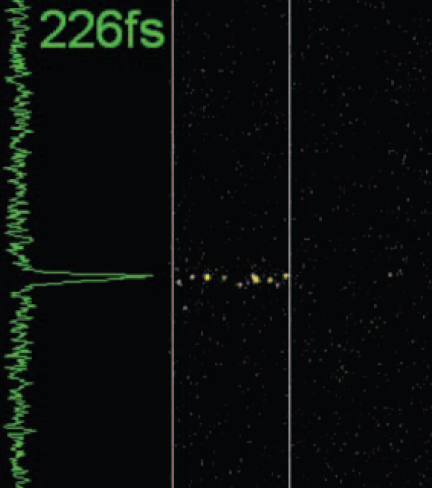
15.9. ábra. A FESCA-2000 (Hamamatsu) sávkamera képe és az abból meghatározott intenzitás profilja egy Ti:zafír lézer impulzusának [15.6].
Ha femtoszekundumos lézerek impulzusainak időbeli alakját akarjuk meghatározni, akkor nemlineáris interferometrikus eszközök állnak rendelkezésre. A 80-as években fejlesztették ki az intenzitás és interferometrikus autokorrelációs módszert [15.7], majd a 90-es évek közepén a FROG (frequency resolved optical gating) [15.8] és a SPIDER (Spectral Phase Interferometry for Direct Electric Field Reconstruction) [15.9] technikát.
Az intenzitás és az interferometrikus autokorrelációs technika közös jellemzője, hogy egy Michelson interferométerre épülnek, melyet a vizsgálandó lézerimpulzussal világítunk meg (15.10. ábra). A nyalábosztón az impulzus kettéválik két azonos időbeli lefutású impulzusra, melyek az interferométer tükreiről visszaverődve a nyalábosztón ismét találkoznak, és együtt lépnek ki az interferométerből. Az interferométer után az impulzusokat ráfókuszáljuk egy nemlineáris kristályra. Ha megfelelő szögben és időben átfedve érkezik a két impulzus, akkor a kristály túloldalán nemcsak az eredeti két impulzus lép ki, hanem a két impulzus frekvenciájának összegével bíró impulzus is. Ez utóbbinak az intenzitását detektáljuk az interferométer egyik tükrének mozgatásával létrehozott időkésleltetés függvényében, azaz a detektor jele
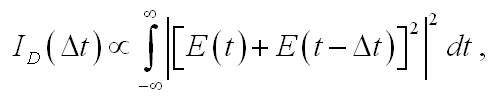 |
(15.8) |
ahol E(t) és E(t - Δt) a két karból egymáshoz képest Δt időkülönbséggel érkező impulzus térerőssége. A kapott jelből iteratív módon lehet visszakövetkezetni az impulzus időbeli alakjára. A módszer hátránya, hogy nem képes különbséget tenni a pozitívan és a negatívan csörpölt impulzus között, azaz mindkét esetben ugyanazt a jelalakot kapjuk. A HeNe lézer ebben az esetben is a tükör mozgatásával bevezetett időkésleltetés meghatározására szolgál.
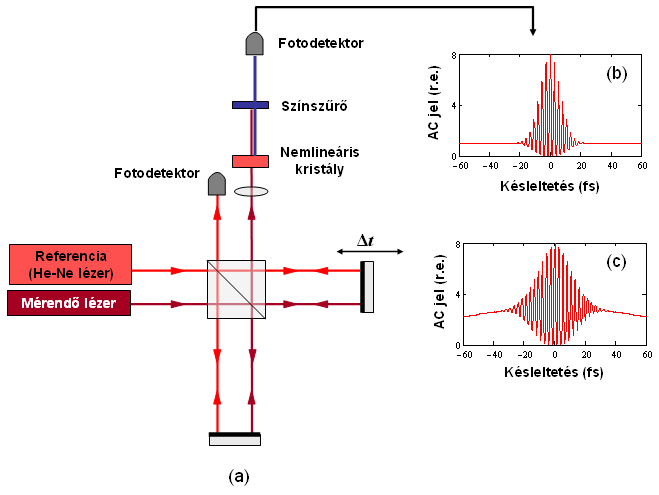
15.10. ábra. (a) Az interferometrikus autokorrelátor felépítése. (b) Egy 10 fs időbeli hosszúságú, 800 nm-es központi hullámhosszú transzformlimitált lézerimpulzus szimulált autokorrelációs jele. (c) Az autokorrelációs jel miután az impulzus keresztülhaladt 1 cm üveglemezen.
A másodharmonikus keltésen alapuló autokorreláció után kifejlesztettek harmadrendű nemlineáris jelenségen alapuló autokorrelátort is, mely már érzékeny a csörp előjelére. Mivel a harmadrendű nemlineáris jelenség még nagyobb intenzitású impulzust igényel, így elsősorban az erősített femtoszekundumos impulzusok esetében használható ez a módszer.
A FROG technika egyik változata, az ún. másodharmonikus keltésen alapuló SHG-FROG nagyon hasonlít az előbb bemutatott másodharmmonikus keltésen alapuló interferometrikus autokorrelátocióhoz. A különbség csak annyi, hogy nem fotodiódával detektáljuk a jelet, hanem a nemlineáris kristály után egy spektrométert helyezünk el, és az összegfrekvencia-keltés során kapott impulzus spektrumát detektáljuk a Δt késleltetés függvényében:
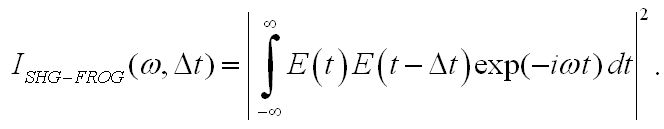 |
(15.9) |
Itt is egy iteratív módszerrel kaphatjuk meg az impulzus időbeli alakját. Az SHG-FROG szintén nem érzékeny a csörp előjelére, ám vannak magasabb rendű nemlineáris jelenségen alapuló FROG módszerek, melyek ezt a problémát megoldják (pl. polarizáció kapuzott, azaz PG-FROG).
A harmadik igen elterjedt módszer a SPIDER. Ebben az esetben is első lépésként megkettőzzük a vizsgálandó impulzust. Ezt megtehetjük olyan formán, hogy egy üveghasáb mellső lapjáról az impulzus egy része visszaverődik, másik része tovább halad az üvegben (15.11. ábra).
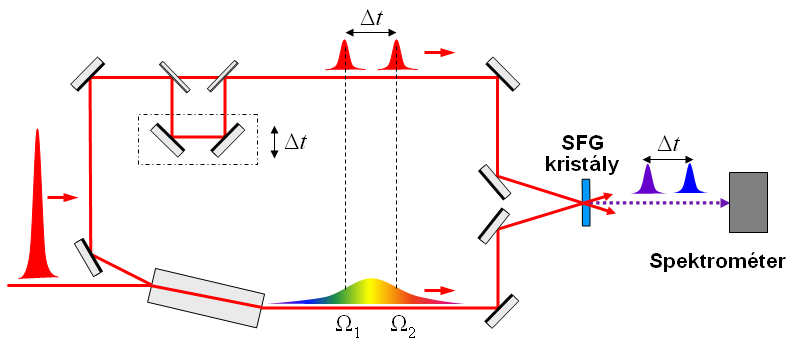
15.11. ábra. A SPIDER elvi felépítése.
Az üveghasábon áthaladó impulzus időben jelentősen megnyúlik, és egyúttal csörpölődik. A másik ágon haladó impulzust ismét megkettőzzük egy Mach-Zehnder interferométerben, és létrehozunk egy Δt időkésleltetést a két azonos időbeli lefutású impulzus között. Ezután a három impulzust egy nemlineáris, esetünkben összegfrekvenciakeltő kristályra küldjük rá. A két impulzus a csörpölt impulzus elején illetve végén lévő komponensekkel együtt halad át a kristályon, melynek hatására két kissé eltérő összegfrekvenciájú impulzus keletkezik, melyek között szintén Δt időkésleltetés van. A két impulzus egy spektrométerbe lép be, és egy modulált spektrumot kapunk a két impulzus interferenciájának eredményeképpen. A modulált spektrum intenzitáseloszlása:
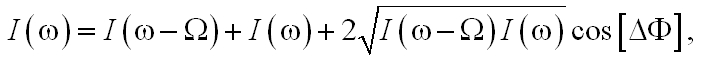 |
(15.10) |
ahol a két impulzus közötti fáziskülönbség:
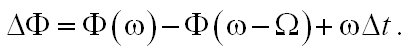 |
(15.11) |
Az interferogram átlagos modulációs periódusát a Δt késleltetés határozza meg. Az interferogramból a Fourier-transzformáción alapuló kiértékelési módszerrel kaphatjuk meg első lépésként a ΔΦ fáziskülönbséget, majd ebből a spektrum ismeretében szintén a Fourier-transzformációt alkalmazva kapjuk meg az impulzus időbeli alakját.
A lézerekből kilépő fénynyaláb iránya változhat az idő függvényében rövidebb (másodperces) vagy hosszabb (akár éves) időskálán. A nyaláb irányának változását okozhatja a laborbeli levegő paramétereinek változása is. A nyalábmozgás ellenőrzésére használható kvadráns detektor vagy CCD kamera (15.12. ábra).
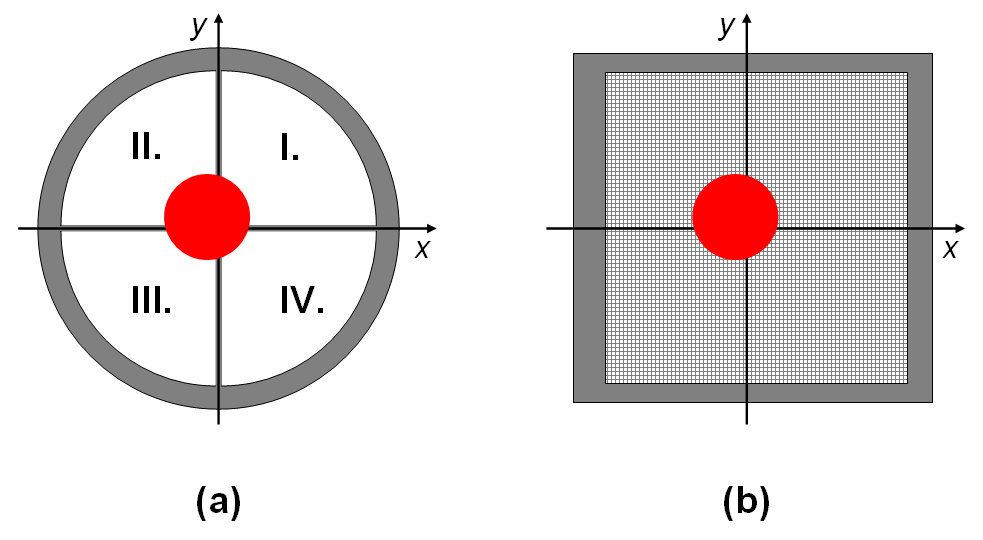
15.12. ábra. A lézernyaláb iránystabilitása detektorral vagy (b) CCD kamerával ellenőrizhető.
A kvadráns detektor esetében a detektor fényérzékeny felülete négy negyedre van osztva (15.12.a ábra). Mindegyik negyedhez egy fémvezeték van rögzítve, így tudjuk mérni a négy negyeden külön külön a fény hatására kialakuló áramot. A nyaláb középpontjának elmozdulására a négy kvadráns áramértékének ismeretében az alábbi egyenleteket felhasználva következtehetünk:
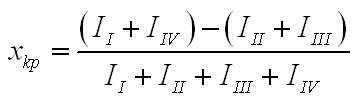 |
, | (15.12) |
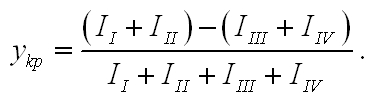 |
(15.13) |
Ha a nyaláb közepe egybeesik a detektor közepével, akkor mind a négy áram azonos erősségű, azaz az Ix és az Iy értéke 0 lesz. Ha a nyaláb elmozdul jobbra az x-tengely irányába, akkor II megegyezik IIV-gyel, valamint az III áramerősség IIII-mal, továbbá teljesül, hogy II > III. Ebben az esetben az Ix > 0 lesz, míg Iy = 0 áll elő. Azaz így jól nyomon követhető, hogy a nyaláb milyen irányban mozdul el. Mivel csak 4 adattal kell dolgoznunk a nyalábhelyzet meghatározásához, így ez a módszer egy nagyon gyors ellenőrzést tesz lehetővé.
A másik megoldás, ha egy CCD vagy CMOS kamerával monitorozzuk a nyalábot. Ekkor mivel a kamerában lévő chipen több millió pixel van, a nyalábközéppontjának meghatározása jóval időigényesebb, ha az ún.intenzitás-középpontot a mechanikából ismert tömegközéppont analógiájára határozzuk meg:
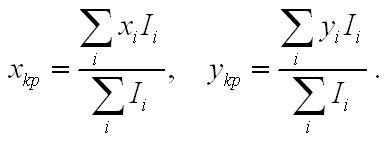 |
(15.14) |
Az időigényesség miatt inkább csak vizuális ellenőrzésnél szokták a kamerát használni.
A lézernyaláb karakterizálását tekintve nemcsak arra az adatra van szükségünk, hogy milyen mértékben mozog a nyaláb az idő függvényében, hanem hogy milyen egy adott helyen a térbeli intenzitáseloszlása. Az ideális lézernyaláb kör keresztmetszetű és Gaussos-intenzitáseloszlású. A valódi lézernyalábok azonban ezt csak legfeljebb megközelítik. Az előbbi részben, a 15.12.b ábrán bemutatott CCD kamerás megoldás lehetővé teszi, hogy pontosan meghatározzuk a nyaláb intenzitását az x és y koordináta függvényében.
Sok esetben a lézernyaláb nemcsak az alap módusból áll, hanem jelen vannak magasabb rendű módusok is, melyek hatására lokális minimumok jelennek meg az amúgy sima függvénnyel leírható intenzitáseloszlásban. Több lézer esetében nem is kör alakú a lézerfolt, de a kamera segítségével pontosan meghatározható az alakja. A lézernyaláb, amikor áthalad lencséken, vagy visszaverődik tükrökről, az alakja torzulhat, amit szintén fontos, hogy mérni tudjunk.
A lézernyaláb egy fontos paramétere a divergenciája. Gauss-nyalábok esetében ez már elméletileg vizsgálva volt a 4. fejezetben. A divergencia mérésének legegyszerűbb módja, ha látható fényű lézerről van szó, hogy egy ernyőt használva lemérjük két, egymástól lehetőleg minél távolabb lévő pontban a nyaláb átmérőjét (15.13. ábra).
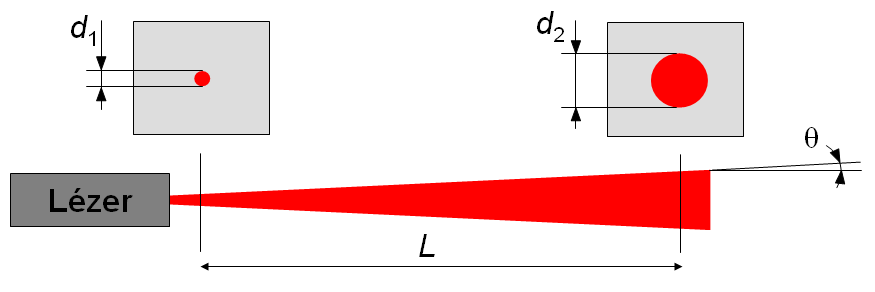
15.13. ábra. A lézernyaláb divergenciájának egyszerű mérése.
A nyaláb divergenciaszögének (θ) közelítő értéke egyszerűen számolható a nyaláb d1 és d2 átmérőjéből, valamint az ernyő két helyzete közötti L távolságból:
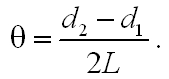 |
(15.15) |
A módszer alkalmazásakor felvetődik, hogy hol van a nyaláb széle. Az ábrával ellentétben a lézernyaláb intezitáseloszlása a szélek felé folyamatosan csökken, így nem lehet pontosan meghatározni az átmérőt.
Ha az ernyő helyett egy CCD chipet használunk detektorként, akkor a korábbi fejezetben a nyalábsugárra bevezetett definíció szerint pontosan le tudjuk olvasni, hogy az intenzitás maximális értéke milyen távolságban csökken le 1/e2 részére. Ez így már pontosabb eredményt ad, de korántsem biztos, hogy a Rayleigh-tartományon kívül végeztük a mérést, azaz lehet, hogy a nyaláb tágulása még nem arányos a távolsággal. Igazán pontos mérést akkor végzünk, ha nem két helyen, hanem jóval több, például 20 helyen is megmérjük a nyaláb átmérőjét a nyalábnyak előtt és után is. A mért értékekre az elméletből adódóan egy gyökös kifejezést illesztünk. Egy valódi lézernyaláb esetében azonban könnyen előfordulhat, hogy az illesztés nem ad pontos eredményt. Ennek az oka, hogy a valódi lézernyalábok esetében a θ divergenciaszög és a nyalábnyak w0 mérete közötti kifejezés az alábbi alakra módosul:
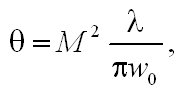 |
(15.16) |
ahol az M2 faktor annak jellemzésére szolgál, hogy a vizsgált lézernyaláb mennyire közelíti meg az ideális Gauss-nyalábot. Ideális esetben az M2 értéke 1-gyel egyenlő. A HeNe lézerek nyalábja elég jól megközelíti az ideális nyalábot, azaz M2 = 1,1 - 1,3. Más lézerek esetében az M2 2-nél is nagyobb értékű lehet. Az M2 értékét azért is fontos tudni egy adott lézernyaláb esetén, mert ha lefókuszáljuk, akkor nagyobb lesz a foltméret, mint az ideális nyaláb esetében lenne. Nagyobb fókuszfolt viszont kisebb intenzitást eredményez.
Tekintettel az M2 paraméter fontosságára, több módszert is kifejlesztettek a mérésére. Első pillantásra azt lehet gondolni, hogy az előbb említett CCD chipes megoldás a célravezető. Ezzel az eszközzel azonban két probléma is van. Ha túl nagy az intenzitás, akkor fényszűrőt kell a chip elé helyezni, csakhogy a szűrő egy planparalel lemez, ami kissé módosítja a nyaláb geometriai jellemzőit. A másik probléma akkor jelentkezik, ha nagyobb a nyaláb átmérője, mint a chip.
Ezen problémák kiküszöbölésére dolgozták ki az ún. késél-módszert. Ennek lényege, hogy egy élet tolunk be a lézernyaláb útjába, és az él mellett elhaladó összes fényt egy fotodiódára gyűjtjük (15.14. ábra).
15.14. ábra. A kés-él módszer kísérleti elrendezése.
Az él mozgatása során (animáció) a mért jel egy TEM00 Gauss-nyaláb esetén az úgynevezett hibafüggvényt adja (15.15. ábra). Akár a mért jelre történő illesztéssel, akár a jel 10%-ához és 90%-ához tartozó Δx érték 0,7803 szorosából adódik a nyalábsugár. Különböző helyeken megmérve a nyalábsugár értékét, a kemarás mérésnél említettek szerint w0 és M2 is meghatározható.
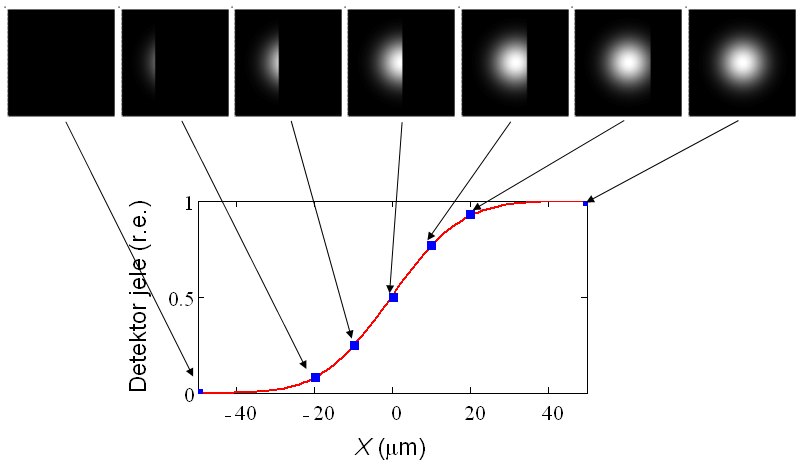
15.15. ábra. A detektor jele az él különböző helyzeténél. A nyalábsugár w = 30 μm.
Sorolja fel a lézerek alkalmazhatósága szempontjából fontos paramétereket!
Hogyan számítható ki a lézer csúcsteljesítménye, ha ismert a lézerimpulzus energiája és időbeli hossza?
Ismertesse a piroelektromos detektor működésének elvét!
Rajzolja le a Fourier-transzformációs spektrométer elvi felépítését! Mi a szerepe a referencia lézernek?
Ismertesse a sávkamera működését! Milyen időbeli hosszúságú optikai jelenségek vizsgálatára használható?
Mi a különbség az interferometrikus autokorrelátor és SPIDER működése között?
Imertesse a lézernyaláb M2 paraméterének a késél módszerrel történő mérésének főbb lépéseit!
[15.1] http://www.coherent.com/downloads/AboutMeasuringLaserPowerndEnergyOutputFinal.pdf
[15.2] https://www.cvimellesgriot.com/Products/Documents/TechnicalGuide/Beam-Measure-Guide.pdf
[15.3] http://www.hamamatsu.com/resources/pdf/ssd/s10356-01_kspd1075e08.pdf
[15.4] http://www.judsontechnologies.com/files/pdf/Ge_shortform_August2004.pdf
[15.5] http://www.oceanoptics.com/technical/hr4000.pdf
[15.6] http://jp.hamamatsu.com/resources/products/sys/pdf/eng/e_c6138.pdf
[15.7] J. C. M. Diels, J. J. Fontaine, I. C. McMichael, F. Simoni: Control and measurement of ultrashort pulse shapes (in amplitude and phase) with femtosecond accuracy, Appl. Opt.24 (1985) 1270.
[15.8] R. Trebino and D. J. Kane: Using phase retrieval to measure the intensity and phase of ultrashort pulses: frequency-resolved optical gating. J. Opt. Soc. Am. A.10 (1993) 1101.
[15.9] C. Iaconis and I. A. Walmsley: Spectral phase interferometry for direct electric-field reconstruction of ultrashort optical pulses, Opt. Lett.23 (1998) 792.